In this work, we formulated a mathematical model to describe growth, acquisition of bacterial resistance, and immune response for Helicobacter pylori (H. pylori). The qualitative analysis revealed the existence of five equilibrium solutions: (ⅰ) An infection-free state, in which the bacterial population and immune cells are suppressed, (ⅱ) an endemic state only with resistant bacteria without immune cells, (ⅲ) an endemic state only with resistant bacteria and immune cells, (ⅳ) an endemic state of bacterial coexistence without immune cells, and (ⅴ) an endemic coexistence state with immune response. The stability analysis showed that the equilibrium solutions (ⅰ) and (ⅳ) are locally asymptotically stable, whereas the equilibria (ⅱ) and (ⅲ) are unstable. We found four threshold conditions that establish the existence and stability of equilibria, which determine when the populations of sensitive H. pylori and resistant H. pylori are controlled or eliminated, or when the infection progresses only with resistant bacteria or with both bacterial populations. The numerical simulations corroborated the qualitative analysis, and provided information on the emergence of a limit cycle that breaks the stability of the coexistence equilibrium. The results revealed that the key to controlling bacterial progression is to keep bacterial growth thresholds below 1; this can be achieved by applying an appropriate combination of antibiotics and correct stimulation of the immune response. Otherwise, when bacterial growth thresholds exceed 1, the bacterial persistence scenarios mentioned above occur.
Citation: Edgar Alberto Vega Noguera, Simeón Casanova Trujillo, Eduardo Ibargüen-Mondragón. A within-host model on the interactions of sensitive and resistant Helicobacter pylori to antibiotic therapy considering immune response[J]. Mathematical Biosciences and Engineering, 2025, 22(1): 185-224. doi: 10.3934/mbe.2025009
| [1] | J. Amador, D. Armesto, A. Gómez-Corral . Extreme values in SIR epidemic models with two strains and cross-immunity. Mathematical Biosciences and Engineering, 2019, 16(4): 1992-2022. doi: 10.3934/mbe.2019098 |
| [2] | Tianqi Song, Chuncheng Wang, Boping Tian . Mathematical models for within-host competition of malaria parasites. Mathematical Biosciences and Engineering, 2019, 16(6): 6623-6653. doi: 10.3934/mbe.2019330 |
| [3] | Prathibha Ambegoda, Hsiu-Chuan Wei, Sophia R-J Jang . The role of immune cells in resistance to oncolytic viral therapy. Mathematical Biosciences and Engineering, 2024, 21(5): 5900-5946. doi: 10.3934/mbe.2024261 |
| [4] | Robert E. Beardmore, Rafael Peña-Miller . Rotating antibiotics selects optimally against antibiotic resistance, in theory. Mathematical Biosciences and Engineering, 2010, 7(3): 527-552. doi: 10.3934/mbe.2010.7.527 |
| [5] | Xiaxia Kang, Jie Yan, Fan Huang, Ling Yang . On the mechanism of antibiotic resistance and fecal microbiota transplantation. Mathematical Biosciences and Engineering, 2019, 16(6): 7057-7084. doi: 10.3934/mbe.2019354 |
| [6] | Jing Jia, Yanfeng Zhao, Zhong Zhao, Bing Liu, Xinyu Song, Yuanxian Hui . Dynamics of a within-host drug resistance model with impulsive state feedback control. Mathematical Biosciences and Engineering, 2023, 20(2): 2219-2231. doi: 10.3934/mbe.2023103 |
| [7] | Hermann Mena, Lena-Maria Pfurtscheller, Jhoana P. Romero-Leiton . Random perturbations in a mathematical model of bacterial resistance: Analysis and optimal control. Mathematical Biosciences and Engineering, 2020, 17(5): 4477-4499. doi: 10.3934/mbe.2020247 |
| [8] | Xiaoxiao Yan, Zhong Zhao, Yuanxian Hui, Jingen Yang . Dynamic analysis of a bacterial resistance model with impulsive state feedback control. Mathematical Biosciences and Engineering, 2023, 20(12): 20422-20436. doi: 10.3934/mbe.2023903 |
| [9] | Helen Moore, Weiqing Gu . A mathematical model for treatment-resistant mutations of HIV. Mathematical Biosciences and Engineering, 2005, 2(2): 363-380. doi: 10.3934/mbe.2005.2.363 |
| [10] | Qimin Huang, Mary Ann Horn, Shigui Ruan . Modeling the effect of antibiotic exposure on the transmission of methicillin-resistant Staphylococcus aureus in hospitals with environmental contamination. Mathematical Biosciences and Engineering, 2019, 16(5): 3641-3673. doi: 10.3934/mbe.2019181 |
In this work, we formulated a mathematical model to describe growth, acquisition of bacterial resistance, and immune response for Helicobacter pylori (H. pylori). The qualitative analysis revealed the existence of five equilibrium solutions: (ⅰ) An infection-free state, in which the bacterial population and immune cells are suppressed, (ⅱ) an endemic state only with resistant bacteria without immune cells, (ⅲ) an endemic state only with resistant bacteria and immune cells, (ⅳ) an endemic state of bacterial coexistence without immune cells, and (ⅴ) an endemic coexistence state with immune response. The stability analysis showed that the equilibrium solutions (ⅰ) and (ⅳ) are locally asymptotically stable, whereas the equilibria (ⅱ) and (ⅲ) are unstable. We found four threshold conditions that establish the existence and stability of equilibria, which determine when the populations of sensitive H. pylori and resistant H. pylori are controlled or eliminated, or when the infection progresses only with resistant bacteria or with both bacterial populations. The numerical simulations corroborated the qualitative analysis, and provided information on the emergence of a limit cycle that breaks the stability of the coexistence equilibrium. The results revealed that the key to controlling bacterial progression is to keep bacterial growth thresholds below 1; this can be achieved by applying an appropriate combination of antibiotics and correct stimulation of the immune response. Otherwise, when bacterial growth thresholds exceed 1, the bacterial persistence scenarios mentioned above occur.
The stomach is not an organ exempt from microbial colonization despite having a hostile environment for a bacterial form to thrive, infect, and generate tissue damage, The above has enabled us to establish links and relationships between gastric diseases and infection by Helicobacter pylori (H pylori). Once the infection occurs, H. pylori is established in the gastric mucus. In that medium, the pathogen makes use of its cellular characteristics that enable it to move through the mucus, reaching the mucosa of the gastric epithelium. Once it is adhered to the epithelial cells, it gives rise to persistent colonization. H. pylori induces a strong immune, humoral, and cellular response in the gastric mucosa of the host, although this does not mean that the infection is eliminated [1].
According to estimates described in [2] by 2015, a prevalence of infection by H. pylori of approximately 4.4 billion individuals was estimated worldwide. The global prevalence landscape reports high rates in regions such as Africa at 79.1%. Moreover, Latin America and the Caribbean have a prevalence rate is 63.4%, and Asia has a prevalence rate at 54.7%. In contrast, the prevalence of H. Pylori infection has lower rates in regions such as North America with a rate of 37.1% and Oceania with 24.4% [2]. On the other hand, H. pylori is also a human pathogen for which increased antibiotic resistance constitutes a serious problem for human health. The increase in antibiotic resistance globally has led to a substantial decrease in the efficacy of treatment against H. pylori and probably to an increased risk in the development of complications such as peptic ulcers and gastric cancer [3]. H. pylori frequently shows different resistance profiles; resistance to a single drug or resistance to multiple drugs. In eradication therapies that combine some of the most common antibiotics such as clarithromycin and metroninazole, it suggests that the main reason for the failure is resistance of H. pylori to one of the antibiotics used; clarithromycin [4]. In 2017, the World Health Organization designated clarithromycin-resistant H. pylori as a high priority for antibiotic research and development [4]. Researchers have also observed that resistance to treatments that include other drugs have been developed; metronidazole, tetracycline, fluoroquinolones and rifamycins for which resistance has become an emerging problem although to a lesser extent [5].
A first approach towards the understanding of cellular activity inside the stomach is given through the mathematical models proposed in [6,7,8], in which the digestive dynamics and the role of gastric acid secretion are described, incorporating in some cases pharmacodynamic and pharmacokinetic aspects. This enables researchers to study the development of diseases related to the secretion of gastric acid and the design of therapies for their control. In the same line that describes stomach dynamics, other mathematical models deepen the study and description of the bacterial population that has the ability to colonize and survive in the gastric box; for example, mathematical models such as those proposed in [9,10,11] are used to analyze the prevalence and persistence of infection by H. pylori in terms of a spatial migration of the pathogen present in the mucus towards the gastric epithelium, including from nutrient consumption by the pathogen for survival at the site of infection and from a level of immune response activated by the host.
On the other hand, with regard to the prevelence of bacterial resistance and the use of pharmacological therapies to counteract infections, there is a broad conceptual framework referring to studies focused on mathematically modeling the acquisition of bacterial resistance of some pathogens in vivo when they are exposed to antibiotic treatments. In [12] and [13] bacterial growth studied to differentiate drug-sensitive and drug-resistant organisms under considerations, where the acquisition of resistance occurs by antibiotic exposure and that the elimination of the pathogen by the drug differs according to its bacteriostatic and bactericidal action. In addition, the mathematical models presented in [14] and [15] describe the dynamics of growth and antibiotic resistance of pathogens considering the acquisition of resistance by means of point mutation mechanisms and by horizontal transfer of plasmids, enabling them to predict the temporal course of the interacting bacterial populations in infectious processes. With the same purpose of modeling the acquisition of bacterial resistance through the exchange of genetic material between pathogens, there are also models proposed in [16] and [17], where the dynamics of bacterial interaction, immune response, and growth of plasmids are studied, the latter is modeled through a functional response that supposes a cellular replication of the plasmids through the generalized law of mass action. Other mathematical models that are used to describe growth and acquisition of resistance are formalized in the models proposed in [18] and [19], in these models, in addition to assuming hypotheses of acquisition of bacterial resistance similar to those described by [12,13,14,15,16] also contemplate together the proliferation of an immune cellular response in the individual, enabling the dynamics of growth, development of resistance, and immune response under the effects of a pharmacological therapy. Therefore, from the academic panorama, a high interest in using mathematical modeling tools and concepts applied to the description and understanding of biological phenomena referred to infectious dynamics in the human being can be evidenced.
The review of specialized literature enables us to frame the scope of our infectious modeling work for H. pylori. On the one hand, the background shows us a series of mathematical models that are used to theoretically describe behaviors at the cellular level that happen during an infectious course generated by bacteria that contemplate, aspects such as: Bacterial growth, acquisition of bacterial resistance, effectiveness of antibiotic treatments and activation, and proliferation of immune mechanisms. The aforementioned aspects are of special interest and are integrated into the model, where we propose to describe the infectious dynamics of H. pylori since, under them, the basic hypotheses of stomach interaction between the host and the pathogen are raised.
On the other hand, the model we formulate is based mainly on the works [18] and [15]. In this way, from a mathematical perspective, we analyze the qualitative dynamics of the formulated model and compare it with the dynamics of the original models on which the main model was based. The contrast of behaviors of the models enables us to identify the emergence of new dynamics or highlight those that have been inherited from the base models. Therefore, the problem of interest lies in describing the infectious persistence of H. pylori in the stomach using a mathematical model, considering the growth of the pathogen at the site of infection, the mechanisms of acquisition of bacterial resistance, and proliferation of the immune response by the host to describe dynamics when the infected subject undergoes a treatment with antibiotics. The content of the work is organized as follows. In the second section, the mathematical model is formulated. In the third and fourth sections, qualitatively analyze of the model. In the fifth section, the numerical results are presented, in the sixth section, additional qualitative results on the behavior of the model solutions in specific subregions of the set of biological interest are presented through discussion. Finally, section seven, we present a general discussion of the work together with the conclusions.
In this section, we formulate a model to describe the growth, acquisition of antibiotic resistance and activation of an immune response, generated in the infection of a human individual with H. pylori.
According to studies and clinical reports, individuals infected with H. pylori develop an ineffective immune response to eradicate the infectious agent. For H. pylori, the inflammatory response is manifested as an active gastritis characterized by the infiltration of leukocytes (lymphocyte T) on the surface of the gastric epithelium. The role of the immune system's innate response is a key factor in the infectious process of H. pylori as it regulates the response of lymphocyte T [1]. The regulatory function of lymphocyte T, known as the regulatory function Th, is a differentiation on the type of response that lymphocyte T will have at the site of infection. For differentiation of the type of response, the antigens of the pathogen must first be recognized through macrophages (mechanism activated in the innate response). After that recognition, there is a release of cytokines that induce the cellular response of lymphocyte T. Depending on the type of predominant cytokines released, the regulatory function Th of lymphocyte T can be Th-1 (T-Helper response type 1), which regulates an increase in the pro-inflammatory response; or a Th-2 (T-Helper type 2) response that regulates an increase in the anti-inflammatory response[20].
The Fitness in genetics describes the ability of an organism to reproduce with a certain genotype, that is, represents the proportion of genes that an organism can inherit in the genes of the next generation. The acquisition of antibiotic resistance usually leads to a loss of fitness in the bacteria which is known as Fitness cost. However, the resistant pathogen may undergo additional mutations that offset the cost of fitness. In the case of H. pylori specialized reports [21,22,23] have sought to determine the compensatory mechanisms of antibiotic resistance in H. pylori and suggest that compensatory mutations may play an important role in the evolution and spread of resistant genes in this bacterial population.
The model formulated here is an adaptation that integrates assumptions of the bacterial dynamics of H. pylori proposed in [9,11], as well as the terms that model and describe the growth and acquisition of bacterial resistance and immune response proposed in [15] and [18], respectively. The model is framed in the following assumptions: 1) H. Pylori has the ability to replicate in epithelial cells once it manages to adhere to them. 2) The model considers an epithelial detachment of H. Pylori towards the gastric mucus when the gastric mucosa layer is overloaded. 3) Bacterial resistance is acquired by exposure to the antibiotic and by transfer of genetic material (conjugation) considered through mass action kinetics. 4) Consider the immune response to H. Pylori infection through a population of T lymphocytes (immune cells) whose regulatory function induces an anti-inflammatory response. 5) Consider increasing the concentration of the antibiotic to reach the equilibrium serum concentration through a rate of drug absorption.
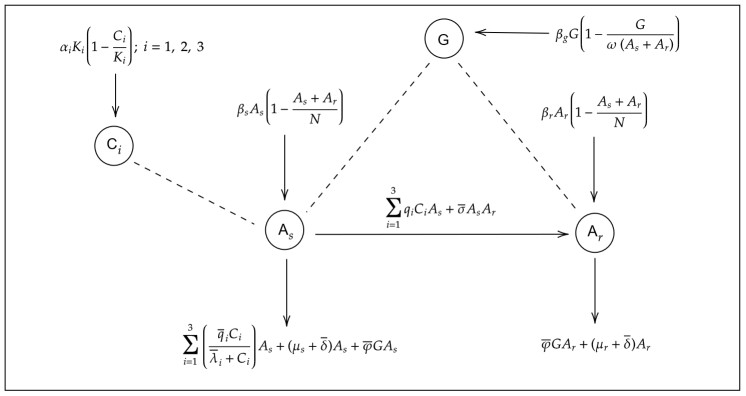
The populations considered in the infectious dynamics of H. pylori are the bacterial population attached to the gastric epithelium, divided into sensitive As(t) and resistant Ar(t). Moreover, the population of lymphocyte T (immune cells) whose regulatory function induces an anti-inflammatory immune response G(t) and the blood concentration of each antibiotic used in an eradication treatment Ci(t);i=1, 2, 3 is included. The bacterial population of H. pylori (sensitive and resistant) on the gastric epithelium is replicated following a logistic growth represented by βsAs(1−As+ArN) and βrAr(1−As+ArN), respectively, with βs and βr such as reproduction rates and load capacity N. We assume that the fact of acquiring resistance generates a fitness cost that is manisfested as a decrease in the reproductive rate of resistant bacteria; therefore, βr≤βs. As in [24,25,26,27], we assume that the bacterial population As dies by the action of antibiotics following a term of maximum saturation (Emax) represented by ∑3i=1(¯qiCiˉλi+Ci)As, where ˉqi represents the maximum rate of elimination of sensitive bacteria of H. pylori per antibiotic effect and ˉλi is the concentration needed for each antibiotic to reach half the maximum elimination rate. Additionally, populations As and Ar have constant per capita mortality rates μs and μr, respectively. On the other hand, the proportion of resistant bacteria emerging due to point mutations that the population As suffers from antibiotic exposure is represented by ∑3i=1qiCiAs, where qi is the rate at which the population As acquires resistance. As in [15,19,28], the proportion of resistant bacteria of H. pylori that emerge by the horizontal exchange of plasmids is represented through a kinetics of mass action whose term is ˉσAsAr, where ˉσ represents the conjugation rate. The saturation of the gastric epithelium forces the bacteria of H. pylori adherent to detach and return to the mucus until the saturation are again below the load levels of the epithelium. Therefore, the model represents the epithelial detachment of each type of bacteria as ˉδAs and ˉδAr where ˉδ is the rate of epithelial detachment. As in [18], we assume, through a logistic term that the proliferation of the immune response, that the recruitment of lymphocyte T that induce an anti-inflammatory response on the gastric epithelium is represented by βgG(1−Gω(As+Ar)), where βg is the recruitment rate of immune cells and the activation capacity of these cells is ω times the amount of bacteria present (As+Ar). The lymphocyte population T acts on the bacterial population by eliminating them at a rate ˉφ; consequently, the terms ˉφAsG and ˉφArG represent the bacterial proportion of H. pylori (sensitive and resistant) that is eliminated by the immune system. We represent the increase in the concentration of each antibiotic used in eradication therapy against H. pylori through the diffusion layer model described in [29], which states that the dissolution of the antibiotic concentration over time occurs proportionally to the difference between the antibiotic saturation rate K and the remaining concentration C over time t. that is, as αi(Ki−Ci)=αiKi(1−CiKi) for i=1,2,3, where αi represents the constant proportionality of increase of each antibiotic and Ki the saturation rate for the drug concentration. The schematic diagram in Figure 1 shows the dynamic interactions of the model.
Therefore, the complete model that describes the dynamics of growth and acquisition of bacterial resistance for H. pylori with immune response is represented by the nonlinear system of ordinary differential equations indicated below.
| dAsdt=βsAs(1−As+ArN)−3∑i=1(¯qiCi¯λi+Ci)As−3∑i=1qiCiAs−ˉσAsAr−ˉφGAs−(μs+δ)AsdArdt=βrAr(1−As+ArN)+3∑i=1qiCiAs+ˉσAsAr−ˉφGAr−(μr+δ)ArdGdt=βgG(1−Gω(As+Ar))dCidt=αiKi(1−CiKi), for i=1,2,3. | (2.1) |
In system (2.1), the parameters βs,βr,βg,T,ˉqi,qi,ˉσ,ˉφ,μs,μr,δ,ω,αi, and Ki are positive for i=1,2,3. To facilitate the analysis of the model represented by the system (2.1) and reduce the number of parameters, the following variable change is introduced
| s=AsN, r=ArN, g=GωN, ci=CiKi for i=1,2,3. | (2.2) |
In terms of the variables (2.2), system (2.1) is rewritten as
| dsdt=βss[1−(s+r)]−3∑i=1(¯qiciλi+ci)s−3∑i=1micis−σsr−φgs−(μs+δ)sdrdt=βrr[1−(s+r)]+3∑i=1micis+σsr−φgr−(μr+δ)rdgdt=βgg(1−g(s+r))dcidt=αi(1−ci); i=1,2,3, | (2.3) |
where
| σ=ˉσN, φ=ˉφωN, λi=¯λiKi, mi=qiKi, for i=1,2,3. | (2.4) |
The region of biological interest of the system (2.3) is given by
| Ω={(s,r,g,c1,c2,c3)∈R6+:0≤s,r≤1; 0≤g≤s+r≤1; 0≤ci≤1}, | (2.5) |
with i=1,2,3. Since the vector field defined by the right side of system (2.3) is C1(Ω), by the theorem of existence and uniqueness, we can guarantee the existence of the solution. In the following proposition, we prove that the system is well posed, in the sense that the solutions with initial conditions in Ω remain there for all t≥0; this means that, we are going to prove that the set Ω is positively invariant.
Lemma 2.1. The region Ω defined in (2.5) is positively invariant with respect to the system (2.3).
The proof of Lemma 2.1 is presented in B.
The equilibria of system (2.3) are given by the solutions of the following algebraic equations
| βss[1−(s+r)]−3∑i=1(¯qiciλi+ci)s−3∑i=1micis−σsr−φgs−(μs+δ)s=0βrr[1−(s+r)]+3∑i=1micis+σsr−φgs−(μr+δ)r=0βgg(1−g(s+r))=0αi(1−ci)=0, for i=1,2,3. | (3.1) |
From the last two equations of system (3.1), we have ci=1 for i=1,2,3, and g=0 or g=s+r. First, we will determine the equilibria of the model for the case ci=1 (i=1,2,3) and g=0, after the case ci=1 (i=1,2,3) and g=s+r.
By replacing ci=1 for i=1,2,3 and g=0 in (3.1), we have
| βss[1−(s+r)]−3∑i=1(¯qiλi+1)s−3∑i=1mis−σsr−(μs+δ)s=0βrr[1−(s+r)]+3∑i=1mis+σsr−(μr+δ)r=0. | (3.2) |
From the first expression of (3.2), we have s=0 or
| βs[1−(s+r)]−3∑i=1(¯qiλi+1)−3∑i=1mi−σr−(μs+δ)=0. |
For s=0, system (3.2) is reduced to
| βrr(1−r)−(μr+δ)r=0. |
Therefore, for s=0, the solutions of (3.2) are given by r=0 or
| r=r1, | (3.3) |
where r1=Rr−1Rr, being
| Rr=βrμr+δ. | (3.4) |
The above implies the existence of the equilibrium E0=(0,0,0,1,1,1), and if Rr>1, then there exists the equilibrium E1=(0,r1,0,1,1,1), and the threshold Rr defined in (3.4) is interpreted as the number of bacteria produced by the fraction of resistant bacteria that detach from the gastric epithelium. Now, for s≠0, the first equation of (3.2) is reduced to
| Rs[1−(s+r)]−Rsrσβs−1=0, |
or equivalently
| s+r(1+σβs)=Rs−1Rs. | (3.5) |
where
| Rs=βs∑3i=1(¯qiλi+1+mi)+μs+δ, | (3.6) |
the threshold Rs defined in (3.6) is interpreted as the number of bacteria produced by the fraction of sensitive bacteria that survive the effects due to antibiotics, that do not present mutations by antibiotic exposure, and that do not detach from the gastric epithelium. We observe from (3.5) that a necessary condition to the existence of sensitve and resistent bacteria is Rs>1. By solving for s in (3.5), we obtain
| s=Rs−1Rs−r(1+σβs). | (3.7) |
From (3.7), it can be inferred that s will be positive when satisfied
| r<ˉr1, | (3.8) |
where ˉr1=(Rs−1Rs)(11+σβs). From the second equation of (3.2), we obtain
| −r2+[(σβr−1)r+3∑i=1miβr]s+r1r=0. | (3.9) |
Replacing (3.7) in (3.9), we obtain
| −r2+[(σβr−1)r+3∑i=1miβr][Rs−1Rs−r(1+σβs)]+r1r=0. |
Making the products and grouping, we have
| −[1+(σβr−1)(1+σβs)]r2+[r1+(σβr−1)(Rs−1Rs)−b1(1+σβs)]r+b1(Rs−1Rs)=0, |
From the above we obtain the following quadratic equation Q(r)=0, where b1=∑3i=1miβr and
| Q(r)=−yor2+y1r+y2, | (3.10) |
where y0, y1, and y2 are constants defined by
| y0=1+(σβr−1)(1+σβs)y1=r1+(σβr−1)(Rs−1Rs)−b1(1+σβs)y2=b1(Rs−1Rs). | (3.11) |
Since bacterial coexistence needs Rs>1, then the third expression of (3.11) implies that y2>0. Also, by rewriting y0 as
| y0=1+(σβr−1)(1+σβs)=σβrβs(βs−βr+σ)>0, |
it is evident that y0>0. In this sense, if Rs>1 the polynomial defined in (3.10) has a single positive solution described by
| r∗=y1+√y21+4y0y22y0. | (3.12) |
replacing (3.12) in the expression (3.7), we obtain
| s∗=Rs−1Rs−r∗(1+σβs). | (3.13) |
Considering the expressions (3.12) and (3.13), we have the equilibrium E∗=(s∗,r∗,0,1,1,1). The following shows the conditions for the existence of E∗ in the region Ω. Indeed, if Rs>1, and considering the expression (3.13), we have that 0<s∗+r∗+r∗σβs<1 from where
| 0<s∗+r∗<1. | (3.14) |
On the other hand, defining
| Rσr=1+σβs1Rs+σβs, | (3.15) |
the condition r1<ˉr1 is equivalent to Rr<Rσr, which guarantees that s∗ is positive. This result is stated in the following lemma.
Lemma 3.1. Let Rs>1. If Rr<Rσr then Q(ˉr1)<0.
Proof of Lemma 3.1 is presented in the C. Now, since Q(0)=y2>0 and Q(ˉr1)<0 follow that r∗<ˉr1, which implies by inequality (3.8) that s∗ is positive. In this way, if Rs>1 and Rr<Rσr then the equilibrium E∗∈Ω.
Now, the equilibria of system (2.3) when ci=1 (i = 1, 2, 3) and g=s+r are given by the solutions of the system of algebraic equations provide
| βss[1−(s+r)]−3∑i=1(¯qiλi+1)s−3∑i=1mis−σsr−φ(s+r)s−(μs+δ)s=0βrr[1−(s+r)]+3∑i=1mis+σsr−φ(s+r)r−(μr+δ)r=0. | (3.16) |
Grouping s in the first equation of system (3.16) we obtain s=0 or
| βs[1−(s+r)]−3∑i=1(¯qiλi+1)−3∑i=1mi−σr−φ(s+r)−(μs+δ)=0. | (3.17) |
For s=0, system (3.16) is reduced to βrr(1−r)−φr2−(μr+δ)r=0, and grouping r in the above equation, we obtain
| r[−(βr+φ)r+βr−(μr+δ)]=0, |
From where r=0 or
| −(βr+φ)r+βr−(μr+δ)=0. | (3.18) |
Therefore, for s=0 the solutions of (3.16) are given by r=0 or r=r2, where r2=r1(11+φβr). The above implies the existence of the equilibrium E0=(0,0,0,1,1,1), and if Rr>1, then there exists the equilibrium E2=(0,r2,r2,1,1,1). Now, for s≠0 the first equation of (3.16) is reduced to
| Rs−Rs(s+r)−φβsRs(s+r)−σβsRsr−1=0, |
The above expression is equivalent to
| sh+r(1+φ+σβs)=Rs−1Rs, | (3.19) |
where h=(1+φβs). From (3.19) we observe that a necessary condition for the existence of sensitive and resistent bacteria is Rs>1. By solving for s in (3.19), we obtain
| s=(Rs−1Rs)1h−r(1+φ+σβs)1h. | (3.20) |
From (3.20) we can be inferred that s will be positive when satisfied
| r<Rs−1Rs(11+σ+φβs), |
or
| r<ˉr2, | (3.21) |
where ˉr2=Rs−1Rs(11+σ+φβs). From the second equation (3.16), we obtain
| −(βr+φβr+φ)r2+(βrβr+φ−1d)r+(σ−(βr+φ)βr+φ)sr+s3∑i=1(miβr+φ)=0. |
After grouping some terms in the previous expression, we come to
| −r2+(Rrd−1d)r+(σβr+φ−1)sr+s3∑i=1(miβr+φ)=0, |
or
| −r2+[(σβr+φ−1)r+b2]s+r2r=0, | (3.22) |
where r2=Rr−1d and b2=∑3i=1(miβr+φ). Replacing (3.20) in (3.22) we obtain
| −r2+[(σβr+φ−1)r+b2][(Rs−1Rs)1h−r(1+φ+σβs)1h]+r2r=0. |
Grouping and reorganizing we have
| −[1+(σβr+φ−1)(1+φ+σβs)1h]r2+[r2+1h(σβr+φ−1)(Rs−1Rs)−b2h(1+φ+σβs)]r+b2h(Rs−1Rs)=0. |
In this way we obtain the following quadratic equation ˉQ(r)=0 and
| ˉQ(r)=−v0r2+v1r+v2, | (3.23) |
where v0, v1 and v2 are constants defined by
| v0=1+(σβr+φ−1)(1+φ+σβs)1hv1=r2+1h(σβr+φ−1)(Rs−1Rs)−b2h(1+φ+σβs)v2=b2h(Rs−1Rs). | (3.24) |
Since bacterial coexistence needs Rs>1, then the third expression of (3.24) implies that v2>0. Also, by rewriting v0 as
| v0=1+(σβr+φ−1)(1+φ+σβs)1h=1+(σβr+φ−1)(1+σβs+φ)=σ(βr+φ)(βs+φ)[βs−βr+σ]>0, |
it is evident that v0. In this way, if Rs>1 the polynomial defined in (3.23) has a single positive solution described by
| r3=v1+√v21+4v0v22v0. | (3.25) |
Replacing (3.25) in expression (3.20), we obtain
| s3=1h[Rs−1Rs−r3(1+φ+σβs)], | (3.26) |
from the expressions (3.25) and (3.26) we have
| g3=1h[Rs−1Rs−r3(1+φ+σβs)]+v1+√v21+4v0v22v0. | (3.27) |
Considering (3.25), (3.26), and (3.27), we have the equilibrium E3=(s3,r3,s3+r3,1,1,1). The following shows the necesary conditions for the existence of E3 in the region Ω. Indeed, if Rs>1 and considering the expression (3.26), we have that 0<s3+r3+1βs[s3φ+r3(φ+σ)]<1, so the previous inequality implies that
| 0<s3+r3<1. | (3.28) |
On the other hand, the condition
| r2<ˉr2, | (3.29) |
guarantees that s3 is positive. The previous result is stated in the following lemma.
Lemma 3.2. Let Rs>1. If r2<ˉr2 then ˉQ(ˉr2)<0.
The proof of Lemma 3.2 is presented in the D. Since ˉQ(0)=v2>0 and ˉQ(ˉr2)<0, it follows that r3<ˉr2, which implies by inequality (3.21) that s3 is positive, and by inequality (3.28) there exists an equilibrium E3 of coexistence with both bacteria. Now defining
| Rφr=11−ˉr2(1+φβr), | (3.30) |
we have the following possibilities: 1) Since Rs>1 and Rr>1, if 0<ˉr2(1+φβr)<1, then 1<Rφr, thus the condition (3.29) is equivalent to Rr<Rφr, which guarantees that s3 is positive and thus there is equilibrium E3 in Ω. 2) If Rs>1, Rr>1, and ˉr2(1+φβr)>1 the we have Rφr<0; thus, the condition (3.29) is equivalent to Rr>Rφr. Therefore, by the Lemma 3.2 and inequality (3.28) also a coexistence equilibrium E3 of coexistence in Ω. If Rs>1 is clear that Rφr cannot be equal to one and by how it is defined as Rφr in (3.30) it is evident that it cannot be equal to zero either. Complementarily, if Rs>1 and 0<ˉr2(1+φβr)<1, then Rφr>1, and if Rs>1 and ˉr2(1+φβr)>1, then Rφr<0. 3) If Rs>1 and Rr≤1 also r2<ˉr2, under this condition, there is an equilibrium E3. The following proposition summarizes the conditions of existence of the equilibrium solutions of system (2.3) in the region Ω.
Theorem 3.3. The equilibrium solutions of system (2.3) are given by
(1) The system (2.3) always has a bacteria-free equilibrium E0=(0,0,0,1,1,1) in Ω.
(2) If Rr>1, we have the following options
(i) there exists an equilibrium without sensitive bacteria and immune response E1=(0,r1,0,1,1,1) in Ω.
(ii) there exists an equilibrium without sensitive bacteria but with an immune response equivalent to bacterial persistence E2=(0,r2,r2,1,1,1) in Ω.
(3) If Rs>1 and Rr<Rσr there exists an equilibrium in which sensitive and resistant bacteria coexist without proliferation of the immune response E∗=(s∗,r∗,0,1,1,1) in Ω.
(4) If Rs>1 and 1<Rr<Rφr, there is an equilibrium in which sensitive and resistant bacteria coexist along with the proliferation of the immune response. E3=(s3,r3,g3,1,1,1) in Ω.
(5) If Rs>1 and Rr>1 but Rφr<0 (Rr>Rφr), there is an equilibrium in which sensitive and resistant bacteria coexist along with the proliferation of the immune response. E3=(s3,r3,g3,1,1,1) in Ω.
(6) If Rs>1 and Rr≤1, then there exists an equilibrium of coexistence with both bacteria and immune response E3=(s3,r3,g3,1,1,1) in Ω.
Figures 2–4 show the existence regions of the equilibrium of the system (2.3) according to the cases that occur between the thresholds R∗r and Rφr.
Thresholds Rs and Rr are interpreted considering the premise of the individual reproductive success of an organism in a population. Generally in population ecology, the measure of individual reproductive success is assumed as the average number of new organisms that are created over the lifetime of a single organism. In this way, when we consider the product of between the rate of bacterial reproduction βs with the half-life time of a bacterium in population As, the individual reproductive success rate of a sensitive adherent bacterium of H. pylori is obtained. This reproductive success is indicated as
| Ns=βs1μs=βsμs. | (3.31) |
The parameter indicated in (3.31) is interpreted as the number of new bacteria produced by a bacterium As of H. pylori during its half-life. Similarly, when the product is taken between the rate of bacterial reproduction βr with the half-life time of a bacterium in the population Ar, the individual reproductive success rate of a resistant adherent bacterium of H. pylori is obtained. This reproductive success is indicated as
| Nr=βr1μr=βrμr. | (3.32) |
The parameter indicated in (3.32) is interpreted as the number of new bacteria produced by a bacterium Ar of H. pylori during its half-life. To give meaning to the threshold Rs, it is rewritten in terms of the individual reproductive success rate Ns. Thus,
| Rs=μs∑3i=1(ˉqiλi+1+mi)+μs+δNs. | (3.33) |
Expression (3.33) is described as the product between the individual reproductive success of a bacterium As of H. pylori and the quotient
| μs∑3i=1(ˉqiλi+1+mi)+μs+δ=1−∑3i=1(ˉqiλi+1+mi)+δ∑3i=1(ˉqiλi+1+mi)+μs+δ. | (3.34) |
In [15], a similar parameter to the expression (3.34) is defined. Thus, here we adopt a biological interpretation in the same sense for said parameter. The difference expressed on the right side of (3.34) can be interpreted by assuming the parameters involved in terms of percentage; in this way, the unit represents 100% of the sensitive bacterial population, and the remaining quotient is understood as the percentage of sensitive bacteria that detach from the gastric epithelium, die from the antibiotic effect, and mutate due to exposure to antibiotics. Later, threshold Rs represents the number of bacteria generated by the fraction of sensitive organisms of H. pylori that remain on the gastric epithelium, evade the elimination action of the drug, and do not have mutations by antibiotic exposure. For threshold Rr a biological interpretation can be made in a similar way, that is, rewrite Rr in terms of individual reproductive success Nr, so that
| Rr=μrμr+δNr. | (3.35) |
Thus, the threshold Rr is described by the product between the reproductive success rate of a bacterium Ar of H. pylori and the quotient μrμr+δ, latter can be rewritten as follows
| μrμr+δ=1−δμr+δ, | (3.36) |
again assuming parameters in terms of percentages the difference described on the right side of (3.36) represents 100% of the resistant bacterial population minus the proportion of resistant bacteria that are detached from the gastric epithelium. Thus the above difference equals the proportion of resistant bacteria that do not detach from the gastric epithelium. Therefore, the threshold Rr defines the number of bacteria generated by the fraction of resistant organisms of H. pylori that do not detach from the gastric epithelium.
The results of Theorem 3.3 establish that:
(a) There is always a balance free of infection by H. pylori, which suggests that both sensitive and resistant populations can be eliminated or controlled with appropriate treatment.
(b) If the average amount of bacteria generated by the fraction of resistant organisms of H. pylori that do not detach from the gastric epithelium is greater than one (Rr>1), then the population of H. pylori resistant bacteria persists without lymphocyte activation T and persists in balance with the proliferation of an immune response that is deficient.
(c) If the number of bacteria generated by the fraction of sensitive organisms of H. pylori that remain on the gastric epithelium, evade the elimination action of the drug and do not present mutations by antibiotic exposure is greater than one (Rs>1)
(ⅰ) the amount of bacteria generated by the fraction of resistant organisms of H. pylori that do not detach from the gastric epithelium is less than Rσr (Rr<Rσr), then both types of H. pylori bacteria coexist without activation of the immune response in the host.
(ⅱ) the amount of bacteria generated by the fraction of resistant organisms of H. pylori that do not detach from the gastric epithelium is greater than one but less than Rφr (1<Rr<Rσr), so both types of H. pylori bacteria coexist along with the proliferation of an inefficient immune response in the host.
(ⅲ) the amount of bacteria generated by the fraction of resistant organisms of H. pylori that do not detach from the gastric epithelium is greater than one (Rr>1) but the threshold Rφr is less than zero (Rφr<0), so persistence occurs with both types of H. pylori bacteria in conjunction with the proliferation of an inefficient immune response in the host.
(ⅳ) the amount of bacteria generated by the fraction of resistant organisms of H. pylori that do not detach from the gastric epithelium is less than or equal to one (Rr≤1) so persistence occurs with both types of H. pylori bacteria in conjunction with the proliferation of an inefficient immune response in the host.
In this section, we determine the local asymptotic stability of the equlibrium solutions of the system (2.3). To this end, we consider the linearization ˙x=J(E)x around an equilibrium E where x=(s,r,g,c1,c2,c3)T, and J is the jacobian of the system evaluted in E given by
| J(E)=[j11(E)−(βs+σ)s−φsj14(E)j15(E)j16(E)j21(E)j22(E)−φrm1sm2sm3sβgg2(s+r)2βgg2(s+r)2j33(E)000000−α1000000−α2000000−α3]. | (4.1) |
with
| j11(E)=βs[1−(s+r)]−βss−3∑i=1(ˉqiciλi+ci+mici)−σr−φg−(μs+δ)j1k(E)=s[−ˉqiλi+ci+ˉqici(λi+ci)2−mi]; k=4,5,6 e i=1,2,3j21(E)=−βrr+3∑i=1mici+σrj22(E)=βr[1−(s+r)]−βrr+σs−φg−(μr+δ)j33(E)=βg(1−2gs+r). |
We begin by analyzing the local stability of the equilibrium E0=(0,0,0,1,1,1), and assume the condition that 0<g=s+r≤1. In this way, the jacobian given (4.2) evaluated in E0 is given by
| J(E0)=[j11(E0)00000∑3i=1mij22(E0)0000βgβg−βg000000−α1000000−α2000000−α3]. | (4.2) |
with
| ξ1,0=j11(E0)=[3∑i=1(ˉqiλi+1+mi)+μs+δ](Rs−1)ξ2,0=j22(E0)=(μr+δ)(Rr−1) |
From the matrix (4.2), we observe that the local stability of equilibrium E0 depends on the sign of eigenvalues ξ1,0 y ξ2,0. In this way, ξ1,0<0 if and only if Rs<1, and ξ2,0<0 if and only if Rr<1. The local stability of the equilibrium E0 is presented in the following result.
Theorem 4.1. If Rs<1 and Rr<1, the trivial solution E0=(0,0,0,1,1,1) is locally asymptotically stable in Ω. If Rs>1 or Rr>1, then E0 is unstable.
Now, we analyze the local stability of the equilibrium E1. To this end, we observe that the Jacobian given in (4.1) evaluated in E1 is given by
| J(E1)=[j11(E1)00000−βrr1+∑3i=1mi+σr1j22(E1)−φr100000βg000000−α1000000−α2000000−α3], | (4.3) |
with
| j11(E1)=βs(1−r1)−σr1−[3∑i=1(ˉqiλi+1+mi)+μs+δ], | (4.4) |
and
| j22(E1)=βr(1−r1)−(μr+δ). | (4.5) |
The characteristic equation associated with the matrix (4.3) is expressed as (α3+ξ)(α2+ξ)(α1+ξ)(ξ−βg)P1(ξ)=0, where P1(ξ)=[j11(E1)−ξ][j22(E1)−ξ] is the characteristic polynomial of the matrix block 2×2
| G1=[j11(E1)0−βrr1+∑3i=1mi+σr1j22(E1)] | (4.6) |
We observe from the characteristic equation J(E1) that one of the eigenvalues of the matrix (4.3) is ξ=βg>0; therefore, the equilibrium E1 is unstable. This result is summarized in the following proposition.
Theorem 4.2. The equilibrium solution E1=(0,r1,0,1,1,1) of the system (2.3) is unstable in Ω.
Now, we analyze the local stability of the equilibrium E1. To this end, we observe that the Jacobian given in (4.1) evaluated in E1 is given by
| J(E1)=[j11(E1)00000−βrr1+∑3i=1mi+σr1j22(E1)−φr100000βg000000−α1000000−α2000000−α3], | (4.7) |
with
| j11(E1)=βs(1−r1)−σr1−[3∑i=1(ˉqiλi+1+mi)+μs+δ], | (4.8) |
and
| j22(E1)=βr(1−r1)−(μr+δ). | (4.9) |
The characteristic equation associated with the matrix (4.3) is expressed as (α3+ξ)(α2+ξ)(α1+ξ)(ξ−βg)P1(ξ)=0, where P1(ξ)=[j11(E1)−ξ][j22(E1)−ξ] is the characteristic polynomial of the matrix block 2×2
| G1=[j11(E1)0−βrr1+∑3i=1mi+σr1j22(E1)] | (4.10) |
We observe from the characteristic equation J(E1) that one of the eigenvalues of the matrix (4.3) is ξ=βg>0, therefore the equilibrium E1 is unstable. This result is summarized in the following proposition.
Theorem 4.3. The equilibrium solution E1=(0,r1,0,1,1,1) of the system (2.3) is unstable in Ω.
Now, we analyze the local stability of the equlibrio E2. The Jacobian given in (4.1) evaluated in E2 is given by
| J(E2)=[j11(E2)00000−βrr2+∑3i=1mi+σr2−βrr2−φr2000βgβg−βg000000−α1000000−α2000000α3]. | (4.11) |
with
| j11(E2)=βs(1−r2)−[3∑i=1(ˉq1λi+1+mi)+μs+δ]−σr2−φr2=Λ2(1d−Rrd+ˉr2)=Λ2(−r2+ˉr2), | (4.12) |
where Λ2=βs(1+σ+φβs). The characteristic equation of (4.11) is expressed as −(α3+ξ)(α2+ξ)(α1+ξ)P3(ξ)=0, where P3(ξ) is the characteristic polynomial of the matrix block 3×3
| G3=[Λ2(−r2+ˉr2)00−βrr2+∑3i=1mi+σr2−βrr2−φr2βgβg−βg]. | (4.13) |
The matrix block G3 has the characteristic equation [Λ2(−r2+ˉr2)−ξ]P4(ξ)=0, where P4(ξ) is a characteristic polynomial of the matrix block 2×2 lower right of the matrix G3
| G4=[−βrr2−φr2βg−βg]. |
In turn, the characteristic equation of G4 is
| P4(ξ)=ξ2+¯η1ξ+¯η2=0, | (4.14) |
where ˉη1=βrr2+βg and ˉη2=βgr2[βr+φ]. We observe that ˉη1>0 and ˉη2>0, by the criterion of Routh-Hurwitz (case n = 2) it follows that the roots of (4.14) are negative or have a real negative part. Later, the characteristic equation of J(E2) is
| (α3+ξ)(α2+ξ)(α1+ξ)[ξ−Λ2(−r2+ˉr2)](ξ2+¯η1ξ+¯η2)=0. | (4.15) |
Thus, all the roots of the polynomial (4.15) have a negative sign, except by the factor [ξ−Λ2(−r2+ˉr2)]. Therefore, is sufficient to examine the variation of the sign of ξ4,2 to determine the local stability of the equilibrium E2. In this way, when
| −r2+ˉr2<0, | (4.16) |
the eigenvalue ξ4,2 will be negative and the equilibrium E2 will be locally asymptotically stable. To describe the stability of E2 in terms of thresholds Rs and Rr, we make the following considerations: 1) If Rr>1 and Rs≤1 it is clear that the condition (4.16) is true and therefore E2 it is locally asymptotically stable. 2) If Rs>1 and 1<Rφr<Rr, where Rφr is defined in (3.30), we have ˉr2<r2, later ξ4,2<0 and therefore E2 it is locally asymptotically stable. The local stability of the equilibrium E2 is summarized in the following result.
Theorem 4.4. The equilibrium solution E2=(0,r2,r2,1,1,1) is locally asymptotically stable in Ω if
(1) Rr>1 and Rs≤1 or (Rs>1 and Rφr<Rr).
The equilibrium E2 is unstable when
(2) Rs>1 and 1<Rr<Rφr or (Rs>1 and Rr>1 but Rφr<0).
Now, we analyze the local stability of the equilibrio E3. The Jacobian given in (4.1) evaluated in E3 is given by
| J(E3)=[−βss3−(βs+σ)s3−φs3j14(E3)j15(E3)j16(E3)j21(E3)j22(E3)−φr3m1s3m2s3m3s3βgβg−βg000000−α1000000−α2000000−α3] | (4.17) |
with
| j21(E3)=−βrr3+3∑i=1mi+σr3,j22(E3)=−1r3[3∑i=1mis3+βrr23],j1k(E3)=s3[−ˉqiλi+1+ˉqi(λi+1)2−mi]; k=4,5,6 and i=1,2,3. |
The characteristic equation of J(E3) is determined by
| −(ξ+α3)(ξ+α2)(ξ+α1)P5(ξ)=0, | (4.18) |
where P5(ξ) is a characteristic polynomial of the matrix block 3×3
| G5=[−βss3−(βs+σ)s3−φs3−βrr3+∑3i=1mi+σr3−1r3[∑3i=1mis3+βrr23]−φr3βgβg−βg]. | (4.19) |
The matrix block G5 has the characteristic equation −ξ3−a1ξ2−a2ξ−a3=0, and when replacing P5(ξ) in (4.18), we obtain
| (ξ+α3)(ξ+α2)(ξ+α1)(ξ3+a1ξ2+a2ξ+a3)=0, | (4.20) |
where
| a1=s2r33∑i=1mi+βrr3+βss3+βg, | (4.21) |
| a2=βg(s3r33∑i=1mi+βrr3+βss3)+βss3Λ3+βgφg3+σs3r3(βs−βr), | (4.22) |
| a3=βsβgs3Λ3+βgφ3∑i=1mis3(1+s3r3)+βgσs3r3(βs−βr). | (4.23) |
From expression (4.20), it can be seen that the eigenvalues ξ1,2=−α3, ξ2,2=−α2 y ξ3,2=−α1 are negative. To study the roots of the equation ξ3+a1ξ2+a2ξ+a3=0 to determine the nature of the equilibrium and stability remains. From (4.21) and (4.23), we observe that a1 as a3 are always positive. On the other hand, when considering the term a1a2−a3, we have
| a1a2−a3=[s3r33∑i=1mi+βrr3+βss3+βg][βg(s3r33∑i=1mi+βrr3+βss)+βss3Λ3+βgφg3+σs3r3(βs−βr)]−[βsβgs3Λ3+βgφ3∑i=1mis3(1+s3r3)+βgσs3r3(βs−βr)], |
| a1a2−a3=(s3r33∑i=1mi)[[βss3Λ3+σs3r3(βs−βr)]+βg(s3r33∑i=1mi+βrr3+βss3)]+βg[βgφg3+βg(s3r33∑i=1mi+βrr3+βss3)]+(βrr3+βss3)[βgφg3+[βss3Λ3+σs3r3(βs−βr)]+βg(s3r33∑i=1mi+βrr3+βss3)]+(s3r33∑i=1mi)βgφg3+βg[βss3Λ3+σs3r3(βs−βr)]−βgs3[βsΛ3+φ3∑i=1mi(1+s3r3)+σr3(βs−βr)]. | (4.24) |
From the last three terms of the expression (4.24), we have
| (s3r33∑i=1mi)βgφg3+βg[βss3Λ3+σs3r3(βs−βr)]−βgs3[βsΛ3+φ3∑i=1mi(1+s3r3)+σr3(βs−βr)]=0, |
thus, a1a2−a3>0 and by Ruth-Hurwitz's criterion, all the roots of the equation ξ3+a1ξ2+a3ξ+a3=0 are negative or have a negative real part. When returning to the characteristic equation of the matrix J(E3)
| (ξ+α3)(ξ+α2)(ξ+α1)(ξ3+a1ξ2+a2ξ+a3)=0, |
we have that all roots are negative or have a real negative part always. This implies that equilibrium E3 is locally asymptotically stable. Figures 5–7 show the stability regions of the equilibrium of system (2.3) according to the case.
Theorem 4.5. The equilibrium solution E3=(s3,r3,s3+r3,1,1,1) is always locally asymptotically stable in Ω.
In this section, we present some numerical simulations of system (2.3), which illustrate the population growth of H. pylori sensitive and resistant to antibiotic therapy, including Rifampicin (RIF), Ciprofloxacin (CIP), and Clarithromycin (CLT), which are antibiotics used in a triple scheme to eradicate the bacteria. The simulations also illustrate the activation of the host's immune response against this pathogen, describing the role of the immune response through lymphocyte T that have been differentiated with a Th−2 response that induce an eradication action of the bacteria. Globally, it is estimated that 60% of the population is infected by this pathogen [30]. Since its discovery, there is no single treatment for its eradication, rather, treatment therapies consist of antibiotic combinations of common antimicrobials (clarithromycin, ciprofloxacin, metronidazole, rifapimycin, and amoxicillin) that are generally used against other infections that affect humans though H. pylori has developed resistance to these. The values of the parameters used in the simulations are positive constants and were determined from a search in clinical and specialized reports on growth, elimination, and bacterial resistance associated with H. pylori and on bacterial resistance in general (see Table 1).
| Parameter | Definition | Value | Reference |
| βs | Reproductive rate of the population As | 16.66 day−1 | [11] |
| βr | Reproductive rate of the population Ar | 9.996 day−1 | Hypothesis |
| βg | Reproductive rate of immune cells G (lymphocytes T) | 0.6 day−1 | [18] |
| N | Carrying capacity of the gastric epithelium | 2.1 × 103 bact | [11] |
| ω | Lymphocyte recruitment capacity T | 1 cel/bact | Hypothesis |
| ˉq1 | Maximum rate of elimination due to antibiotic effect c1 | 36 day−1 | [31] |
| ˉq2 | Maximum rate of elimination due to antibiotic effect c2 | 36 day−1 | [31] |
| ˉq3 | Maximum rate of elimination due to antibiotic effect c3 | 36 day−1 | [31] |
| q1 | Mutation rate due to antibiotic exposure of RIF | 6.6 × 10−8 ml/(mg⋅day) | [32] |
| q2 | Mutation rate due to antibiotic exposure of CIP | 3.8 × 10−8 ml/(mg⋅day) | [32] |
| q3 | Mutation rate due to antibiotic exposure of CLT | 3 × 10−9ml/(mg⋅day) | [32] |
| ˉλ1 | Antibiotic concentration when reached ¯q1/2 | 0.00025 mg/ml | [31] |
| ˉλ2 | Antibiotic concentration when reached ¯q2/2 | 0.00025 mg/ml | [31] |
| ˉλ3 | Antibiotic concentration when reached ¯qi/2 | 0.00025 mg/ml | [31] |
| ˉσ | Mutation rate by plasmid transfer | 1 × 10−5 (bact⋅ day)−1 | Hypothesis |
| ˉφ | Rate of bacterial elimination by immune cells | 6 ×10 −6 (cell⋅ day)−1 | [19] |
| μs | Natural death rate of the population As | 0.0037 day−1 | [33] |
| μr | Natural death rate of the population Ar | 0.0037 day−1 | [33] |
| δ | Rate of detachment of bacteria from the gastric epithelium | 0.5 day−1 | [11] |
| α1 | Constant of proportion increased concentration of RIF | 0.96 | [13] |
| α2 | Constant of proportion increased concentration of CIP | 0.45 | Hypothesis |
| α2 | Constant of proportion increased concentration of CLT | 0.35 | Hypothesis |
| K1 | Antibiotic saturation concentration RIF | 0.0012 mg/(ml⋅day) | [34] |
| K2 | Antibiotic saturation concentration CIP | 0.0025 mg/(ml⋅day) | [35] |
| K3 | Antibiotic saturation concentration CLT | 2.77 mg/(ml⋅day) | [36] |
The trivial equilibrium solution E0 always exists in the biological interest set. This equilibrium can be stable only if the number of bacteria produced by the fraction of sensitive organisms of H. pylori that escape the antibiotic effect, that do not mutate and do not detach from the gastric epithelium is less than one (Rs<1), as well as the amount of bacteria produced by the fraction of resistant organisms of H. pylori that do not detach from the gastric epithelium below the unit (Rr<1), in any other case, the trivial equilibrium is unstable. Figure 8 shows the numerical solution of system (2.3) when βr=0.664, βs=16.66 and μs=μr=0.37; thus; it can be observed that the population densities of sensitive and resistant bacteria tend to be eliminated. The first, either by the antibiotic effects of the therapy or by immune response, the second, because the population density of resistant bacteria in this case does not exceed the threshold of persistence (Rr>1). In addition, the immune response described by the activation of immune cells tends to be reduced, like the population of H. pylori. In short, under the conditions described, the system evolves biologically towards equilibrium. E0, represents, a scenario where an equilibrium free of infection is reached.

On the other hand, the equilibrium E2 exists when the persistence threshold Rr satisfies that Rr>1. The numerical solution presented in Figure 9 represents, according to the value of the thresholds Rs and Rr respectively, that the time evolution of system (2.3), in this case, occurs towards the equilibrium solution E2. This equilibrium solution can be stable under two scenarios: The first when the number of bacteria produced by the fraction of sensitive organisms of H. pylori that escape the antibiotic effect, that do not mutate and do not detach from the gastric epithelium is less than or equal to one (Rs≤1) and the amount of bacteria produced by the fraction of resistant bacteria that do not prey on the gastric epithelium is greater than one (Rr>1), as seen in the Figure 9. The second stability scenario can occur when the number of bacteria produced by the fraction of sensitive organisms of H. pylori that escape the antibiotic effect, that do not mutate, and that do not detach from the gastric epithelium is greater than one (Rs>1) and the amount of bacteria produced by the fraction of resistant bacteria that do not detach from the gastric epithelium exceeds the threshold Rφr (Rφr<Rr). In these scenarios, it can be evidenced that the population density of H. pylori sensitive tends to be eliminated either as a consequence of eradication therapy or by the immune response, whereas, the resistant population of the pathogen experiences growth from the beginning to a maximum limit that is equaled with the level of immune response in the host.

Numerical simulations enable us to observe an interesting behavior in the stability of equilibrium E3 within the region of biological interest Ω. Local qualitative analysis indicated that equilibrium E3, when it exists, is locally stable, and this equilibrium solution has the particularity that it emerges when equilibrium E2 loses stability or equilibrium E2 does not exist in Ω. In Figure 10 numerical solution illustrates one of the scenarios of coexistence with both bacteria of H. pylori that can emerge, in this case, according to the thresholds because the equilibrium E2 loses local stability. However, the simulations of system (2.3) show numerical evidence that the equilibrium E3 can emerge in Ω but the trajectories seem to approach a limit cycle that generates periodic solutions. When system parameters (2.3) are set to certain numeric values but the carrying capacity of the gastric epithelium increases to N = 2.1× 108, a coexistence equilibrium emerges E3 according to the thresholds: Rs=3.1285, Rr=19.853, Rσr=1.0209 y Rφr=−0.23528. However, the simulations give evidence that the stability of the equilibrium is broken, and the numerical solutions that are generated have periodic behavior. (see Figure 11). When evaluating the numerical approximation of equilibrium E3 generated by the values of the parameters produced by the periodic solutions of the Figure 11 in the Jacobian matrix (4.1), we observe numerical evidence that all the proper values of this matrix J(E3) have a negative real part corroborating the local qualitative analysis in which it was determined that the mere existence of E3 in Ω is sufficient to be locally stable. Additionally the non-appearance of proper values with no real part or of a pair of pure conjugated imaginaries, it also shows numerically that the change in system dynamics (2.3) (arising of periodic solutions) it does not occur by a Hopf type bifurcation, leaving an interesting question from the mathematical point of view about the nature of the bifurcation that is occurring in the system.


Qualitative analysis of the model reveals the existence of equilibrium solutions in two scenarios; The first is where the immune response is suppressed, and the second is where an activation of immune cells occurs. Under a scenario of suppression of the immune response, qualitative analysis shows the existence of a balance free of bacteria or infection, E0. Additionally, when the immune response is inactivated, there are two balances of persistence, one with resistant bacteria E1, and another of coexistence with both bacterial populations E∗. These latter balances have the particularity of being unstable in the region Ω. On the other hand, in a scenario where the immune response is not totally suppressed, the study of the model characterizes two equilibria of infectious persistence of H. pylori; one where the level of immune response finds an equilibrium with the population density of resistant bacteria of H. pylori E2, and another where bacteria coexist by evading the response of immune cells that are activated E3. Bacterial coexistence of H. pylori can emerge because bacterial persistence E2 ceases to exist in Ω or because this same equilibrium loses its local stability, these are sufficient conditions for this solution to be locally stable.
Another infectious scenario that enables the model to be studied is generated when s=0 and ci=1 (i=1,2,3). Under these conditions, system (2.3) is reduced to the planar system
| drdt=βrr(1−r)−φr2−(μr+δ)rdgdt=βgg(1−gr), | (6.1) |
defined in the subregion
| Ω2={(0,r,g,1,1,1)∈R6+;0<g≤r≤1}⊂Ω. | (6.2) |
The planar system (6.1) enables us to describe the interaction of resistant bacteria of H. pylori and immune cells (lymphocyte T) in a scenario where antibiotic saturation in the blood has been reached, and the immune response has not been suppressed, so that the elimination of the bacterial population occurs either by the effect of the drug (sensitive bacteria) or by the activated immune response (resistant bacteria). The qualitative analysis of the system (6.1) is described in the following propositions.
Theorem 6.1. For 0<r0=g0<1, if βr(1−r0)>φr0+(μr+δ), then the region Ω2 is positively invariant by the system (6.1).
Proof. It is easy to verify that the vector field of (6.1) restricted to ∂Ω2, and does not point to the exterior of Ω2.
Theorem 6.2. If Rr>1, the planar system (6.1) has a single equilibrium of persistence E2=(0,r2,r2,1,1,1) in Ω2.
Proof. It follows from the characterization of system equilibriums (2.3) for the case g=s+r with s=0 y ci=1 (i=1,2,3) presented in the Section 3.2.
Theorem 6.3. Equilibrium E2=(0,r2,r2,1,1,1)∈Ω2 of the planar system (6.1) is locally asymptotically stable.
Proof. It follows from the linearization of the system (6.1) around a hyperbolic equilibrium solution E, which is determined by
| ˙x=J(E)x, |
where x=(r,g)T and the Jacobian matrix of the system is determined as
| J(E)=[(βr+φ)(−2r+r2)00βg(1−2gr)]. | (6.3) |
Theorem 6.4. System (6.1) defined in region Ω2 it has no periodic orbits.
Proof. Region Ω2 is simply connected. Defining Φ(r,g)=1rg for r>0, and g>0 it is clear that Φ(r,g) is C1(Ω2). On the other hand, it is not difficult to verify that
| ∇⋅[Φ(r,g)X(r,g)]≠0, |
where X(r,g) is the right side of the system (6.1). Then, by Dulac's criterion, it follows that there are no periodic solutions for system (6.1) in Ω2.
The qualitative results presented above allow us to identify a subregion of Ω invariant by the system (6.1) that is not on the border of Ω. On this subregion, there are no periodic solutions, and there is a single equilibrium of persistence only with resistant bacteria of H. pylori E2, which is always locally stable. In contrast, when the solution E2 is at Ω−Ω2 it can have locally stable and unstable behaviors (see Section 4). From proposition 6.3, we interpret biologically that, under the conditions described above, it is possible to have a scenario of infectious persistence of H. pylori where the immune response of the host is not suppressed; however, despite being active, it is evaded or is not strong enough to control bacterial progression. In addition, antibiotic treatment cannot control or eliminate the population of the pathogen. The clinical literature on infection and immune response against H. pylori describes some strategies of the pathogen involved in the evasion of the immune response [37,38], which play a role in favor of the pathogen and allow it to go unnoticed on the host's defenses, generating an infectious persistence. These strategies depend on other factors and variables that are not related in the model formulated here, which represents a limitation when delving into the biological interpretation of the scenarios predicted by the model with these characteristics, leaving aspects to be considered in future research.
In this article, we adapted and formulated a mathematical model from the antibiotic resistance models of [18] and [15], and applied to the dynamics of bacterial growth and immune response of H. pylori. The infectious dynamics between sensitive and resistant bacteria of the pathogen, immune cells, and antibiotics were explored and described under the assumption that bacterial resistance develops through two mechanisms: Mutations by antibiotic exposure and plasmid transfer. The qualitative analysis of the model revealed the existence of equilibrium solutions in two scenarios: The first was where the immune response is suppressed, and the second was where an activation of immune cells occurs. In a scenario of suppression of the immune response, the existence of a balance free of bacteria or infection E0 was shown. Additionally, in this scenario, there were also two equilibriums of persistence; One with only resistant bacteria E1 and another of coexistence with both bacterial populations E∗. On the other hand, in a scenario where the immune response was not suppressed, there were two balances of infectious persistence of H. pylori; one where the level of immune response found a balance with the population density of resistant bacteria E2, and another where bacteria coexisted by evading the response of immune cells that were activated E3.
We found four thresholds that determine the existence and stability of these equilibriums: Rs, Rr, Rσr, and Rφr. Threshold Rs represents the number of bacteria generated by the fraction of sensitive organisms of H. pylori that are kept on the gastric epithelium, and do not present mutations and escape the antibiotic action. Similarly, the threshold Rr represents the amount of bacteria generated by the fraction of resistant organisms of H. pylori that do not detach from the gastric epithelium. On the other hand, thresholds Rσr and Rφr control the progression of infection when sensitive and resistant bacteria of H. pylori coexist in scenarios with suppression and non-suppression of the immune response, respectively.
When Rs<1 and Rr<1, the solutions approximate the bacteria-free equilibrium, which indicates that the populations of H. pylori sensitive and resistant are eliminated by a pharmacological effect (ideal choice of antibiotic therapy) and by the activation of G (lymphocyte T). As manifested in [15] an interpretation of the above result can be described as follows: When H. pylori bacteria that survive both antibiotic treatment and immune system response cannot continue with their reproductive processes, then the infection will be controlled or eliminated. Equilibrium solutions where the immune response is suppressed, E1 and E∗ are unstable in Ω; however, when Rr>1 and Rr<Rσr on the border subregion, Ω1, solutions approach the balance of infectious persistence only of resistant bacteria E1, and when Rs>1 and Rr<Rσr, on this same region, the solutions are approaching equilibrium E∗. If Rr>1 and Rs≤1 or (Rs>1 and Rr<Rφr) sensitive bacteria are eliminated by immune cells or by the antibiotic, infectious persistence is generated only by the H. pylori resistant population, and the immune response is leveled with the population density of the pathogen. In the above scenario, the solutions approach equilibrium E2. When equilibrium E2 loses its local stability or does not exist in Ω, a balance of bacterial coexistence emerges E3 with both types of bacteria of H. pylori.
The numerical simulations presented in Figures 8–10, were made using data from the Table 1, and we can observe that they corroborate the scenarios predicted by the model. In addition, numerical simulations such as the one presented in the Figure 11 give numerical evidence of the occurrence of a bifurcation that generates periodic solutions when the equilibrium of coexistence emerges E3. The numerical description of the proper values of J(E3) provides information on the non-appearance of null proper values or a pair of pure conjugated imaginaries when the emergence of periodic solutions is observed numerically, suggest that the change in system dynamics (2.3) is not of a hopf bifurcation nature.
When we compared the results of the qualitative analysis of system (2.3) regarding the results of the model described in [18], both models have an infection-free equilibrium; however, in our case, this can be locally stable. In both models, equilibrium solutions are obtained with suppression of the immune response and without suppression of it. In [18] the equilibriums without immune response are unstable, in our model they are unstable inside Ω; on the border, there is a region where they can be very stable. In [18], the equilibrium of persistence with bacterial coexistence that does not suppress the immune response is globally stable, and in our model, we have numerical information of a change in stability that would indicate that the orbits of the system approach a cycle limit which would rule out a globlally stable behavior. From the comparison respect to the results of the model described in [15] we observed that both models haven equilibria in a scenario free of infection, showing persistence only with resistant bacteria and persistence with coexistence. The differences lie in the emergence of coexistence equilibrium; in [15], persistence with both types of bacteria emerges when the scenario of infectious persistence with resistant bacteria becomes unstable. Thus, equilibrium of coexistence can break its local stability by making periodic solutions emerge that are theoretically characterized with the occurrence of a Hopf type. In our model, bacterial coexistence emerges in two ways: The first similar to that described in [15], i.e., the persistence of resistant bacteria becomes unstable, but it can also emerge because this persistence of resistant bacteria does not occur within Ω. In addition, in our model, the numerical evidence of the change of dynamics in the equilibrium solution E3 suggests not to be Hopf in nature.
The qualitative results presented in this paper showed predictive scenarios related to the infectious course of H. pylori in the stomach according to some results described in clinical and laboratory studies. First, the model highlights the possibility of a scenario in which the bacterial population of H. pylori can acquire bacterial resistance but cannot reproduce so that the infection can be controlled or eliminated (equilibrium E0). In this sense, the model suggested the possibility of finding an adequate combination between proliferation of immunological mechanisms (T cells) and administration of antibiotics that are effective in treating the infection. Additionally, the model established biological scenarios that can be differentiated according to whether the host's immune response is suppressed (equilibrium E1 and E∗) or not (equilibrium E2 and E3), and generating an infectious persistence only with a resistant population or through a bacterial coexistence. Being more specific, the clinical evidence suggests that, in an infectious process of H. pylori, this pathogen can induce a low activity of T lymphocytes, which leads to a suppression of the immune response so that the only mechanism to fight the infection is through antimicrobial treatment, but when the population acquires resistance, this is not successful. The equilibria of the model that reflect the previous scenario (equilibrium E1 and E∗ in the subregion Ω1) show the possibility that H. pylori bacteria acquire resistance while reproducing, inducing a low regulation of immune mechanisms that can be interpreted as a suppression of the immune response causing bacterial persistence. On the other hand, specialized studies also give evidence that H. pylori has mechanisms that when deployed generate an evasion of immune activity, resulting in immunological proliferation that is not efficient. The equilibria of the model that reflect the previous scenario (equilibrium E2 and E3 in the Ω region) show the possibility that H. pylori bacteria can acquire resistance, and reproduce and despite having an activation and proliferation of immune response, this is not effective. In summary, the model has enabled us to explore and consider certain hypotheses that have come close to describing the infectious phenomenon from the variables and parameters defined in it.
Our work leaves some questions that enable us to perform future research. For example, from the mathematical point of view, we can study and theoretically characterize the nature of the bifurcation that occurs in the system when the equilibrium of coexistence emerges E3. We can also perform research from a perspective related to the infectious process, antibiotic resistance to H. pylori, and the immune response of the host. Moreover, the model considers basic aspects of this phenomenon in the future, so is possible to add more specific variables and parameters that are involved with the immune response deployed in the infection against this pathogen.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
We want to thank anonymous referees for their valuable comments that helped us to improve the paper. Edgar Alberto Vega Noguera acknowledges the Program "Bécate Nariño 2018" and the CEIBA Foundation for the support and assistance provided. Eduardo Ibarguen-Mondragón acknowledges support from Universidad de Nariño.
The authors declare there is no conflict of interest.
Proof. By adding the first two equations of the system (2.3), we obtain
| dsdt+drdt=(βss+βrr)[1−(s+r)]−3∑i=1(¯qiciλi+ci)s−φg(s+r)−(μs+δ)s−(μr+δ)r. | (A.1) |
From the Eq (A.1), we have
| dsdt+drdt≤(βss+βrr)[1−(s+r)]. | (A.2) |
Since it was assumed that βr≤βs, it follows that
| dsdt+drdt≤(βss+βrr)[1−(s+r)]≤(βss+βsr)[1−(s+r)]. |
or
| ddt(s+r)≤βs(s+r)[1−(s+r)]. | (A.3) |
The solution for s+r in Eq (A.3) is
| s(t)+r(t)=(s(0)+r(0))eβst(1−(s(0)+r(0)))+(s(0)+r(0))eβst, | (A.4) |
when 0≤s(0)+r(0)≤1, we have
| 0≤s+r≤(s(0)+r(0))eβst(1−(s(0)+r(0)))+(s(0)+r(0))eβst≤1. | (A.5) |
Expression (A.5) enables us to determine that solutions for s+r satisfy 0≤s(t)+r(t)≤1 for everything t≥0. Additionally, the solutions of the last three equations of (2.3) are obtained through integration, and the solution ci(t) is expressed as
| ci(t)=1−Mie−αit, for i=1,2,3. | (A.6) |
Evaluating (A.6) for t=0, we have to ci(0)=1−Mie−αi(0) for i=1,2,3; thus, the value of the constant will be Mi=1−ci(0), for i=1,2,3. Replacing Mi in the solution (A.6), we obtain
| ci(t)=1−[1−ci(0)]e−αit, for i=1,2,3, | (A.7) |
where ci(0) satisfies 0≤ci(0)≤1. Later, Equation (A.7) concludes that 0≤ci(t)≤1 for all t≥0.
Complementarily, to find the solution of the third equation of (2.3), we assume (s+r) as a constant value, so the solution for g is
| g(t)=(s+r)keβgt1+keβgt, | (A.8) |
evaluating (A.8) for t=0 we have
| g(0)=(s+r)keβg(0)1+keβg(0), | (A.9) |
where the value of the constant is k=g(0)(s+r)−g(0), so the expression (A.9) is rewritten as
| g(t)=(s+r)eβgt((s+r)−g(0))+g(0)eβgt. | (A.10) |
We demonstrate that if 0≤s(0)+r(0)≤1 then 0≤s+r≤1 for t≥0, so when 0≤g(0)≤s+r≤1, con t≥0 we have
| 0≤(s+r)eβgt((s+r)−g(0))+g(0)eβgt≤s+r≤1, | (A.11) |
from the expression (A.11) it follows that the function g(t) satisfies
| 0≤g≤s+r≤1, t≥0. |
Last, the vector field defined by (2.3) to the border of Ω, is when an initial condition is taken x0∈∂Ω, so the solution ϕt(x0) does not contain points for the exterior of Ω. In this way, any solution that starts in the region of biological interest remains in Ω for t≥0. Thus, the region is well defined and positively invariant by the system (2.3).
Proof. Inequality Rr<Rσr is equivalent to −ˉr1+r1<0, and replacing ˉr1 in the previous inequality, we have
| −Rs−1Rs(1+σβs)+r1<0. | (B.1) |
Adding the terms (Rs−1Rs)(σβr−1)−b1(1+σβs) in both sides of the inequality (B.1) and rearranging, we obtain
| −(Rs−1Rs)(σβr−1)−(Rs−1Rs(1+σβs))+(Rs−1Rs)(σβr−1)+r1+b1(1+φ+σβs)<−b1(1+σβs). |
Grouping
| −(Rs−1Rs(1+σβs))[(σβr−1)(1+σβs)+1]+r1+(Rs−1Rs)(σβr−1)−b1(1+σβs)<−b1(1+σβs). |
Replacing the coefficients of (3.11) in the previous inequality, we have
| −y0ˉr1+y1<−b1(1+σβs). | (B.2) |
Note that the right side of inequality (B.2) can be expressed as
| −b1(1+σβs)=−b111+σβs(Rs−1Rs)(Rs−1Rs), |
or
| −b1(1+σβs)=−y2ˉr1. | (B.3) |
Replacing (B.3) in inequality (B.2), we obtain −y0ˉr1+y1<−y2ˉr1, and rearranging the previous inequality follows that
| −y0(ˉr1)2+y1ˉr1+y2<0. |
The left member of the above inequality corresponds to the polynomial Q(r) evaluated in ˉr1, so Q(ˉr1)<0.
Proof. When 0<ˉr2(1+φβs)<1, the inequality Rr<Rφr is equivalent to
| −ˉr2+r2<0. | (C.1) |
Replacing ˉr2 in the previus inequality, we have
| −Rs−1Rs(1+φ+σβs)+r2<0. | (C.2) |
Adding the terms
| 1h(Rs−1Rs)(σβr+φ−1)−b2h(1+φ+σβs), | (C.3) |
in both sides of the inequality (C.1, ) we obtain
| [1h(Rs−1Rs)(σβr+φ−1)−b2h(1+φ+σβs)]−Rs−1Rs(1+φ+σβs)+r2−[1h(Rs−1Rs)(σβr+φ−1)−b2h(1+φ+σβs)]<0. |
Rearranging
| −1h(Rs−1Rs)(σβr+φ−1)−(Rs−1Rs(1+φ+σβs))+1h(Rs−1Rs)(σβrφ−1)+r2+b2h(1+φ+σβs)<−b2h(1+φ+σβs). |
Grouping
| (Rs−1Rs(1+φ+σβs))[−1h(σβr+φ−1)(1+φ+σβs)−1]+r2+1h(Rs−1Rs)(σβrφ−1)−b2h(1+φ+σβs)<−b2h(1+φ+σβs). |
Raplacing in the coefficients of (3.24) in the previus inequality, we have
| −v0ˉr2+v1<−b2h(1+φ+σβs). | (C.4) |
Noting that the right side of inequality (C.1) can be expressed as
| −b2h(1+φ+σβs)=−b2h11+φ+σβs(Rs−1Rs)(Rs−1Rs), |
or
| −b2h(1+φ+σβs)=−v2ˉr2. | (C.5) |
Replacing (C.5) in inequality (C.4), we obtain −v0ˉr2+v1<−v2ˉr2. Rearranging the previus inequality provides
| −v0(ˉr2)2+v1ˉr2+v2<0. |
The left member of the above inequality corresponds to the polynomial ˉQ(r) evaluated in ˉr2, so ˉQ(ˉr2)<0.
| [1] | E. C. García, R. García-González, Helicobacter pylori y la respuesta inmune, Rev. Latinoam. Patol. Clin. Med. Lab., 62 (2015), 112–118. |
| [2] |
J. K. Y. Hooi, W. Y. Lai, W. K. Ng, M. M. Y. Suen, Global prevalence of Helicobacter pylori infection: systematic review and meta-analysis, Gastroenterology, 153 (2017), 420–429. https://doi.org/10.1053/j.gastro.2017.04.022 doi: 10.1053/j.gastro.2017.04.022

|
| [3] |
E. Tshibangu-Kabamba, Y. Yamaoka, Helicobacter pylori infection and antibiotic resistance from biology to clinical implications, Nat. Rev. Gastroenterol. Hepatol., 18 (2021), 613–629. https://doi.org/10.1038/s41575-021-00449-x doi: 10.1038/s41575-021-00449-x

|
| [4] |
A. Savoldi, E. Carrara, D. Y. Graham, M. Conti, E. Tacconelli, Prevalence of antibiotic resistance in Helicobacter pylori: A systematic review and Meta-analysis in World Health Organization Regions, Gastroenterology, 155 (2018), 1372–1382. https://doi.org/10.1053/j.gastro.2018.07.007 doi: 10.1053/j.gastro.2018.07.007

|
| [5] |
F. Megraud, TH pylori antibiotic resistance: prevalence, importance, and advances in testing, Gut, 53 (2004), 1374–1384. https://doi.org/10.1136/gut.2003.022111 doi: 10.1136/gut.2003.022111

|
| [6] |
I. M. Joseph, Y. Zavros, J. L. Merchant, D. Kirschner, A model for integrative study of human gastric acid secretion, J. Appl. Physiol., 94 (2003), 1602–1618. https://doi.org10.1152/japplphysiol.00281.2002 doi: 10.1152/japplphysiol.00281.2002

|
| [7] |
S. Marino, The importance of an inter-compartmental delay in a model for human gastric acid secretion, Bull. Math. Biol., 65 (2003), 963–990. https://doi.org/10.1016/s0092-8240(03)00046-6 doi: 10.1016/s0092-8240(03)00046-6

|
| [8] |
D. Sud, I. M. Joseph, D. Kirschner, Predicting eficacy of proton pump inhibitors in regulating gastric acid secretion, J. Biol. Syst., 12 (2004), 1–34. https://doi.org/10.1142/s0218339004000999 doi: 10.1142/s0218339004000999

|
| [9] |
M. J. Blaser, D. E. Kirschner, Dynamics of Helicobacter pylori colonization in relation to the host response, Proc. Natl. Acad. Sci. U.S.A., 96 (1999), 8359–8364. https://doi.org/10.1073/pnas.96.15.8359 doi: 10.1073/pnas.96.15.8359

|
| [10] |
I. M. Joseph, D. Kirschner, A model for the study of Helicobacter pylori interaction with human gastric acid secretion, J. Theor. Biol., 228 (2004), 55–80. https://doi.org/10.1016/j.jtbi.2003.12.004 doi: 10.1016/j.jtbi.2003.12.004

|
| [11] |
D. E. Kirschner, M. J. Blaser, The dynamics of Helicobacter pylori infection of the human stomach, J. Theor. Biol., 176 (1995), 281–290. https://doi.org/10.1006/jtbi.1995.0198 doi: 10.1006/jtbi.1995.0198

|
| [12] |
E. Ibargüen-Mondragón, S. Mosquera, M. Cerón, E. M. Burbano-Rosero, S. P. Hidalgo-Bonilla, L. Esteva, et al., Mathematical modeling on bacterial resistance to multiple antibiotics caused by spontaneous mutations, BioSystems, 117 (2014), 60–67. https://doi.org/10.1016/j.biosystems.2014.01.005 doi: 10.1016/j.biosystems.2014.01.005

|
| [13] | J. Romero, E. Ibargüen-Mondragón, Sobre la resistencia bacteriana hacia antibióticos de acción bactericida y bacteriostática, Rev. Integración, 32 (2014), 101–116. |
| [14] |
E. Ibargüen-Mondragón, J. P. Romero-Leiton, L. Esteva, E. M. Burbano-Rosero, Mathematical modeling of bacterial resistance to antibiotics by mutations and plasmids, J. Biol. Syst., 24 (2016), 129–146. https://doi.org/10.1142/s0218339016500078 doi: 10.1142/s0218339016500078

|
| [15] |
E. Ibargüen-Mondragón, J. Romero, P. Jhoana, L. Lourdes, M. Gómez Cerón, S. P. Hidalgo-Bonilla, Stability and periodic solutions for a model of bacterial resistance to antibiotics caused by mutations and plasmids, Appl. Math. Model., 76 (2019), 238–251. https://doi.org/10.1016/j.apm.2019.06.017 doi: 10.1016/j.apm.2019.06.017

|
| [16] |
E. Ibargüen-Mondragón, M. C. Gómez, E. M. Burbano-Rosero, Assessing the role of bacterial plasmid replication in a competition model of sensitive and resistant bacteria to antibiotics, AIMS Math., 6 (2021), 9446–9467. https://doi.org/10.3934/math.2021549 doi: 10.3934/math.2021549

|
| [17] |
E. Ibargüen-Mondragón, K. Prieto, S. P. Hidalgo-Bonilla, A model on bacterial resistance considering a generalized law of mass action for plasmid replication, J. Biol. Syst., 29 (2021), 375–412. https://doi.org/10.1142/s0218339021400118 doi: 10.1142/s0218339021400118

|
| [18] |
B. Daşbaşı, İ. Öztürk, Mathematical modelling of bacterial resistance to multiple antibiotics and immune system response, SpringerPlus, 5 (2016), 1–17. https://doi.org/10.1186/s40064-016-2017-8 doi: 10.1186/s40064-016-2017-8

|
| [19] |
B. Daşbaşı, İ. Öztürk, On the stability analysis of the general mathematical modeling of bacterial infection, Int. J. Eng. Appl. Sci., 10 (2018), 93–117. https://doi.org/10.24107/ijeas.445520 doi: 10.24107/ijeas.445520

|
| [20] |
S. Arenillas, A. Godoy, H. Einisman, D. García, P. Harris, Regulación de la respuesta inmune frente a la infección por Helicobacter pylori, Rev. Chil. Pediatr., 73 (2003), 108–115. https://doi.org/10.4067/s0370-41062002000200002 doi: 10.4067/s0370-41062002000200002

|
| [21] |
B. Bjorkholm, M. Sjolund, Mutation frequency and biological cost of antibiotic resistance in Helicobacter pylori, Proc. Natl. Acad. Sci. U.S.A., 98 (2001), 14607–14612. https://doi.org/10.1073/pnas.241517298 doi: 10.1073/pnas.241517298

|
| [22] |
A. Hanafi, W. Lee, M. F. Loke, X. Teh, A. Shaari, M. Dinarvand, et al., Molecular and proteomic analysis of levofloxacin and metronidazole resistant Helicobacter pylori, Front. Microbiol., 7 (2016), 1–12. https://doi.org/10.3389/fmicb.2016.02015 doi: 10.3389/fmicb.2016.02015

|
| [23] |
A. Handel, R. Regoes, R. Antia, The role of compensatory mutations in the emergence of drug resistance, PLoS Comput. Biol., 2 (2006), 1262–1270. https://doi.org/10.1371/journal.pcbi.0020137 doi: 10.1371/journal.pcbi.0020137

|
| [24] |
D. J. Austin, R. M. Anderson, Studies of antibiotic resistance within the patient, hospitals and the community using simple mathematical models, Philos. Trans. R. Soc. London, Ser. B, 354 (1999), 721–738. https://doi.org/10.1098/rstb.1999.0425 doi: 10.1098/rstb.1999.0425

|
| [25] |
M. Jacobs, N. Grégoire, W. Couet, J. B. Bulitta, Distinguishing antimicrobial models with different resistance mechanisms via population pharmacodynamic modeling, PLoS Comput. Biol., 12 (2016), 1–19. https://doi.org/10.1371/journal.pcbi.1004782 doi: 10.1371/journal.pcbi.1004782

|
| [26] |
M. Lipsitch, B. R. Levin, The population dynamics of antimicrobial chemotherapy, Antimicrob. Agents Chemother., 41 (1997), 363–373. https://doi.org/10.1128/aac.41.2.363 doi: 10.1128/aac.41.2.363

|
| [27] |
M. Nikolaou, V. H. Tam, A new modeling approach to the effect of antimicrobial agents on heterogeneous microbial populations, J. Math. Biol., 52 (2006), 154–182. https://doi.org/10.1007/s00285-005-0350-6 doi: 10.1007/s00285-005-0350-6

|
| [28] |
K. Paterson, A. Hoyle, G. Ochoa, C. Baker-Austin, N. G. Taylor, Optimising antibiotic usage to treat bacterial infections, Sci. Rep., 6 (2016), 1–10. https://doi.org/10.1038/srep37853 doi: 10.1038/srep37853

|
| [29] | P. Macheras, A. Iliadis, Modeling in Biopharmaceutics, Pharmacokinetics, and Pharmacodynamics: Homogeneous and Heterogeneous Approaches, Springer Cham, New York, 2006. http://doi.org/10.1007/978-3-319-27598-7 |
| [30] | W. Otero, M. Gómez, L. Otero, A. Trespalacios, Helicobacter pylori: cómo se trata en el 2018?, Rev. Gastroenterol. Peru., 38 (2018), 54–63. |
| [31] |
A. Handel, E. Margolis, B. R. Levin, Exploring the role of the immune response in preventing antibiotic resistance, J. Theor. Biol., 256 (2008), 655–662. https://doi.org/10.1016/j.jtbi.2008.10.025 doi: 10.1016/j.jtbi.2008.10.025

|
| [32] |
G. E. Wang, J. M. Trevor, Q. Jiang, D. E. Taylor, Spontaneous mutations that confer antibiotic resistance in Helicobacter pylori, Antimicrob. Agents Chemother., 45 (2001), 727–733. https://doi.org/10.1128/aac.45.3.727-733.2001 doi: 10.1128/aac.45.3.727-733.2001

|
| [33] |
J. Faghri, F. Poursina, S. Moghim, H. Z. Esfahani, B. N. Esfahani, H. Fazeli, et al., Morphological and bactericidal effects of different antibiotics on Helicobacter pylori, Jundishapur J. Microbiol., 7 (2014), 1–6. https://doi.org/10.5812/jjm.8704 doi: 10.5812/jjm.8704

|
| [34] |
S. Fujimura, S. Kato, T. Kawamura, A. Watanabe, In vitro activity of rifampicin against Helicobacter pylori isolated from children and adults, J. Antimicrob. Chemother., 49 (2002), 541–543. https://doi.org/10.1093/jac/49.3.541 doi: 10.1093/jac/49.3.541

|
| [35] |
E. Begg, R. Robson, D. A. Saunders, G. G. Graham, R. C. Buttimore, A. M. Neill, et al., The pharmacokinetics of oral fleroxacin and ciprofloxacin in plasma and sputum during acute and chronic dosing, Br. J. Clin. Pharmacol., 49 (2000), 32–38. https://doi.org/10.1046/j.1365-2125.2000.00105.x doi: 10.1046/j.1365-2125.2000.00105.x

|
| [36] |
D. Mainz, K. Borner, P. Koeppe, J. Kotwas, H. Lode, Pharmacokinetics of lansoprazole, amoxicillin and clarithromycin after simultaneous and single administration, J. Antimicrob. Chemother., 50 (2002), 699–706. https://doi.org/10.1093/jac/dkf172 doi: 10.1093/jac/dkf172

|
| [37] | R. Mejías-Luque, M. Gerhard, Immune Evasion Strategies and Persistence of Helicobacter Pylori, Springer International Publishing, New York, 2017. https://doi.org/10.1007/978-3-319-50520-63 |
| [38] |
A. Karkhah, S. Ebrahimpour, M. Rostamtabar, V. Koppolu, S. Darvish, V. K. R. Vasigala, et al., Helicobacter pylori evasion strategies of the host innate and adaptive immune responses to survive and develop gastrointestinal diseases, Microbiol. Res., 218 (2019), 49–57. https://doi.org/10.1016/j.micres.2018.09.011 doi: 10.1016/j.micres.2018.09.011

|
| Parameter | Definition | Value | Reference |
| βs | Reproductive rate of the population As | 16.66 day−1 | [11] |
| βr | Reproductive rate of the population Ar | 9.996 day−1 | Hypothesis |
| βg | Reproductive rate of immune cells G (lymphocytes T) | 0.6 day−1 | [18] |
| N | Carrying capacity of the gastric epithelium | 2.1 × 103 bact | [11] |
| ω | Lymphocyte recruitment capacity T | 1 cel/bact | Hypothesis |
| ˉq1 | Maximum rate of elimination due to antibiotic effect c1 | 36 day−1 | [31] |
| ˉq2 | Maximum rate of elimination due to antibiotic effect c2 | 36 day−1 | [31] |
| ˉq3 | Maximum rate of elimination due to antibiotic effect c3 | 36 day−1 | [31] |
| q1 | Mutation rate due to antibiotic exposure of RIF | 6.6 × 10−8 ml/(mg⋅day) | [32] |
| q2 | Mutation rate due to antibiotic exposure of CIP | 3.8 × 10−8 ml/(mg⋅day) | [32] |
| q3 | Mutation rate due to antibiotic exposure of CLT | 3 × 10−9ml/(mg⋅day) | [32] |
| ˉλ1 | Antibiotic concentration when reached ¯q1/2 | 0.00025 mg/ml | [31] |
| ˉλ2 | Antibiotic concentration when reached ¯q2/2 | 0.00025 mg/ml | [31] |
| ˉλ3 | Antibiotic concentration when reached ¯qi/2 | 0.00025 mg/ml | [31] |
| ˉσ | Mutation rate by plasmid transfer | 1 × 10−5 (bact⋅ day)−1 | Hypothesis |
| ˉφ | Rate of bacterial elimination by immune cells | 6 ×10 −6 (cell⋅ day)−1 | [19] |
| μs | Natural death rate of the population As | 0.0037 day−1 | [33] |
| μr | Natural death rate of the population Ar | 0.0037 day−1 | [33] |
| δ | Rate of detachment of bacteria from the gastric epithelium | 0.5 day−1 | [11] |
| α1 | Constant of proportion increased concentration of RIF | 0.96 | [13] |
| α2 | Constant of proportion increased concentration of CIP | 0.45 | Hypothesis |
| α2 | Constant of proportion increased concentration of CLT | 0.35 | Hypothesis |
| K1 | Antibiotic saturation concentration RIF | 0.0012 mg/(ml⋅day) | [34] |
| K2 | Antibiotic saturation concentration CIP | 0.0025 mg/(ml⋅day) | [35] |
| K3 | Antibiotic saturation concentration CLT | 2.77 mg/(ml⋅day) | [36] |
| Parameter | Definition | Value | Reference |
| βs | Reproductive rate of the population As | 16.66 day−1 | [11] |
| βr | Reproductive rate of the population Ar | 9.996 day−1 | Hypothesis |
| βg | Reproductive rate of immune cells G (lymphocytes T) | 0.6 day−1 | [18] |
| N | Carrying capacity of the gastric epithelium | 2.1 × 103 bact | [11] |
| ω | Lymphocyte recruitment capacity T | 1 cel/bact | Hypothesis |
| ˉq1 | Maximum rate of elimination due to antibiotic effect c1 | 36 day−1 | [31] |
| ˉq2 | Maximum rate of elimination due to antibiotic effect c2 | 36 day−1 | [31] |
| ˉq3 | Maximum rate of elimination due to antibiotic effect c3 | 36 day−1 | [31] |
| q1 | Mutation rate due to antibiotic exposure of RIF | 6.6 × 10−8 ml/(mg⋅day) | [32] |
| q2 | Mutation rate due to antibiotic exposure of CIP | 3.8 × 10−8 ml/(mg⋅day) | [32] |
| q3 | Mutation rate due to antibiotic exposure of CLT | 3 × 10−9ml/(mg⋅day) | [32] |
| ˉλ1 | Antibiotic concentration when reached ¯q1/2 | 0.00025 mg/ml | [31] |
| ˉλ2 | Antibiotic concentration when reached ¯q2/2 | 0.00025 mg/ml | [31] |
| ˉλ3 | Antibiotic concentration when reached ¯qi/2 | 0.00025 mg/ml | [31] |
| ˉσ | Mutation rate by plasmid transfer | 1 × 10−5 (bact⋅ day)−1 | Hypothesis |
| ˉφ | Rate of bacterial elimination by immune cells | 6 ×10 −6 (cell⋅ day)−1 | [19] |
| μs | Natural death rate of the population As | 0.0037 day−1 | [33] |
| μr | Natural death rate of the population Ar | 0.0037 day−1 | [33] |
| δ | Rate of detachment of bacteria from the gastric epithelium | 0.5 day−1 | [11] |
| α1 | Constant of proportion increased concentration of RIF | 0.96 | [13] |
| α2 | Constant of proportion increased concentration of CIP | 0.45 | Hypothesis |
| α2 | Constant of proportion increased concentration of CLT | 0.35 | Hypothesis |
| K1 | Antibiotic saturation concentration RIF | 0.0012 mg/(ml⋅day) | [34] |
| K2 | Antibiotic saturation concentration CIP | 0.0025 mg/(ml⋅day) | [35] |
| K3 | Antibiotic saturation concentration CLT | 2.77 mg/(ml⋅day) | [36] |