The effect of PrEP uptake and adherence on the spread of HIV in the presence of casual and long-term partnerships

1.   Introduction

The Center for Disease Control (CDC) estimates that over 1 million adults and adolescents in the USA are currently living with HIV. Gay, bisexual, and other men who have sex with men are the population most affected by HIV. In 2018, $86 \%$ of the 37,832 new HIV diagnoses were among males, while gay and bisexual men, in particular, accounted for $69\%$ ^[1,2]. In 2019 the U.S. Department of Health and Human Services (HHS) proposed the Ending the HIV Epidemic: A Plan for America initiative ^[3] to end the HIV epidemic in the United States within 10 years. This initiative will leverage critical scientific advances in HIV prevention, diagnosis, treatment, and care by coordinating the highly successful programs, resources, and infrastructure of many HHS agencies and offices.

Although HIV testing and promotion of condom use will always be core strategies for reducing risk, a more radical approach is needed for people at high risk who do not have HIV and whose condom use is inconsistent. One such approach is encouraging the use of antiretroviral pre-exposure prophylaxis (PrEP), the FDA-approved daily oral medication regimen, such as Truvada (approved in 2012) or Descovy (approved in 2019), designed to protect people from HIV infection. To qualify for PrEP, a person must be HIV-negative, sexually active, and either 1) infrequently use condoms during sex with one or more partners of either positive or unknown HIV status who are known to be at substantial risk of HIV infection or 2) have had a sexually transmitted infection (STI) with syphilis, gonorrhea, or chlamydia within the past 6 months ^[4]. In the U.S., the CDC estimates that more than one million people (1,232,000 ^[1]) are at sufficient risk for HIV to meet PrEP prescribing guidelines. In contrast, the recent estimate (first quarter of 2017) of people currently taking PrEP (based on pharmacy data) is approximately 120,000, making it about $10 \%$ of those who could benefit from the prophylaxis ^[2].

More than 15 trials (including iPrEx, PROUD, and IPERGAY) of oral PrEP have shown that, when taken consistently and correctly, PrEP is very effective and reduces the chances of HIV infection to near-zero ^[5,6,7]. This has led some to describe PrEP as a "game changer" for HIV prevention. The effectiveness of PrEP is closely linked to adherence - if someone taking PrEP regularly misses daily dose, their risk of HIV infection will increase substantially. It is therefore important that any program offering PrEP provides a combination package of prevention initiatives, based on an individual's circumstances - with support and advice on the importance of PrEP adherence.

In the clinical research world, researchers use the term "men who have sex with men" (MSM) to describe gay and bisexual men, transgender women, and others who were born male and who have sex with men but who may or may not identify as gay or bisexual. The CDC estimates MSM population in the USA to be over 7 million. Current guidelines and recommendations for PrEP use include MSM as one of the priority populations for PrEP implementation. In these guidelines, PrEP is indicated for MSM who are at "substantial risk" of infection, defined primarily by three behavioral criteria: unprotected anal intercourse (UAI) in HIV status-unknown monogamous partnerships, UAI outside of monogamous partnership, and anal intercourse in a known-serodiscordant (mixed HIV-status) partnership ^[4]. Although approximately $25 \%$ of HIV-uninfected MSM aged between 18 and 59 years who report past-year sex with a man meet indications for PrEP use, current PrEP treatment coverage is well below the half million who are eligible ^[8]. Understanding the impact of increased PrEP uptake on population-level HIV incidence should help the public health officials with increasing the PrEP awareness, administration, and adherence.

Mathematical models provide one approach to estimating PrEP impact, but PrEP models of MSM to date have been limited and often differ from the CDC guidelines. A variety of methods have been used to study HIV transmission dynamics in the presence of PrEP. For instance, Kim et al. ^[9] in South Korea, Punyacharoensin et al. ^[10,11] in the UK, and Li et al. ^[12] in China, used compartmental mathematical models with varying number of compartments based on the stages of disease progression, disease diagnosis and treatment. Recently Steinegger et al. ^[13] used network models to demonstrate that efficacy of PrEP determines the best strategy to reducing HIV spread, and that targeting those at highest risk is optimal only if the efficacy of PrEP is above a calculated threshold. Alternatively Jenness et al. ^[14] in the US used an agent-based model in which uniquely identifiable sexual partnership dyads were simulated and tracked over time. The findings published by all of the authors confirmed the positive impact of PrEP on the HIV dynamics. Jenness et al. ^[14] estimated the percentage of infections averted and the number of individuals needed to be treated with PrEP in order to prevent one new infection. Their results suggested that with $40 \%$ coverage of high-risk MSM and $62 \%$ high adherence among those covered, PrEP would eliminate $33 \%$ of new infections among MSM in the USA over the next 10 years. Increasing coverage and adherence jointly raises the percentage of infections averted, but reduction to the number of individuals needed to treat was associated with better adherence only. Across all levels of coverage, increasing the proportion of MSM receiving PrEP who are highly adherent will strongly affect the efficiency of PrEP: the number needed to treat could be reduced from approximately 50 with poor adherence to 20 with optimal adherence ^[14].

This work will focus on the spread of HIV with implementation of PrEP in a homogeneous (sexually-active MSM) population, where the transmission of a disease due to homosexual acts is the highest mode of infection. Unlike the data simulation models presented above, ours will be an analytic model described by the autonomous system of ordinary differential equations. This approach will allow us to understand the effect of different parameter values on the dynamics of the disease, to explore the impact of varying conditions associated with PrEP use, and to define the conditions under which the disease can be eliminated or brought to steady state. The novel feature of our model is consideration of various partnership scenarios, including casual and long-term partnerships. Among the many parameters, the presented model takes into the account rates of acquiring new partners, duration of the long partnerships, rates at which susceptibles start and stop the pre-exposure prophylaxis program, treatment adherence rate and effectiveness rate of PrEP.

A few of the recent publications have addressed some of these aspects but, as far as we are aware, none have combined all of them. Simpson and Gumel ^[15] presented a model with casual partnerships, stratifying the susceptible population using PrEP based on two levels (low and high) of treatment adherence. Silva and Torres ^[16] focused on the population of Cape Verde in the model that includes rates of initiating and defaulting on the presumably $100\%$ effective PrEP treatment and hence not allowing a possibility of disease transmission from that group. Hansson et al. ^[17] proposed a classic pair-formation model that includes steady and casual partners among the individuals categorized as sexually high active and low active. Different mixing patterns are considered but only those highly active sexually are offered PrEP. In addition, those who begin using PrEP are assumed to stay on it indefinitely, with no adherence factor present. Our work confirms that considering only casual partnerships does not provide accurate representation of the disease progression in the long run. Hence the inclusion of long-term partnerships to show their significant impact on the spread of HIV. As reported by Simpson and Gumel ^[15], we also show that adherence plays a very important role, possibly even more than increasing the PrEP uptake by itself. However, while Simpson and Gumel used two levels of compliance, our adherence parameter $q$ varies continuously between $0$ and $1$. Thus we are able to determine the level of compliance necessary to get the reproduction number $R < 1$. Hansson's et al. ^[17] approach of looking at different types or partnerships and also the level of sexual activity is interesting but the assumption of individuals never stopping the strict PrEP regime is highly unrealistic considering the data ^[1].

The model and results of this paper will be presented as follows. In Section 2 we describe the $PSI$ (PrEP-treated, susceptible, infected) model and consider three cases based on the type of partnership(s) each of them includes, calculate the corresponding rates of infection and reproduction numbers, and lastly prove the existence and global stability of equilibria under appropriate conditions. Section 3 presents numeric results, where we look at the time series of all three cases and analyze the elasticity of the reproduction number as well as the sensitivity of the model to its key parameters. In Section 4 we discuss our model and the results as well as point out the limitations and mention future work.

2.   Models

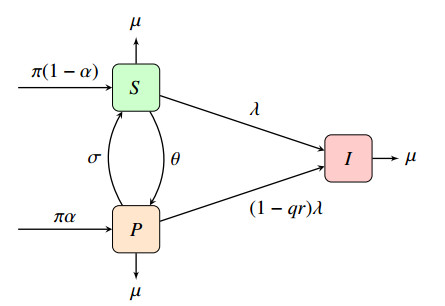
The population being modeled here consists of sexually active MSM individuals ($18$ to $65$ years old), regardless of their HIV status or qualifications for PrEP. We divide the total population, assumed to be constant $N_0$, into two susceptible groups and one infected group. The susceptible individual cannot spread the disease and is either currently taking PrEP (group $P$) or is not taking PrEP but might be a possible candidate for it (group $S$). The infected individual (group $I$) contracted HIV, and can spread the disease. There is only one infectiousness group because we do not distinguish between acute and chronic/latent phases of infection. To maintain a system that is easier to analyze, we currently do not account for differences based on race, age or other demographic factors within the population. In order to explore the possible effect of introducing PrEP to susceptible population before they become sexually active, we introduce a parameter $\alpha$.

Individuals join the sexually active population at a rate $\pi$. Assuming $\alpha$ is a proportion of those starting PrEP beforehand, the individuals enter the model (Figure 1) either through the group $P$, at a rate $\pi \alpha$, or the group $S$, at a rate $\pi (1-\alpha)$. People move from $S$ to $I$ at a rate of infection $\lambda$. However, the rate of infection at which people move from $P$ to $I$ is modulated by a factor $(1-qr)$, which represents the degree of protection of PrEP users who adhere to the treatment at the level $q$, with the treatment effectiveness $r$. In addition, the susceptible individual in $S$ who qualifies for and starts the PrEP treatment moves to $P$ at a rate of $\theta$. At the same time, the people in $P$ who stop the treatment move back to $S$ at the rate of $\sigma$. Each group can be exited due to natural death, migration, or changes in sexual behavior, at a combined removal rate $\mu$. We assume that the individuals diagnosed as HIV positive have ready access to highly effective HAART treatment. HAART treatment cannot cure HIV; it can, however, delay or prevent the onset of symptoms or progression to AIDS, thereby prolonging survival in people infected with HIV ^[18]. With that in mind, we do not consider death or other removal from population due to disease.

The equations governing the model in Figure 1 are given by

The parameters present in the Figure 1 and in the model (2.1) are listed in Table 1. Values of the rates of starting ($\theta$), stopping ($\sigma$), and adherence ($q$) to the PrEP treatment, are assumed minimal due to variability and range of values mentioned in current literature ^[2,10,16].

For the simplicity of work that follows, it is convenient to transform the model (2.1) into an equivalent model with proportions $v = \frac{P}{N_{0}}$, $s = \frac{S}{N_{0}}$, and $i = \frac{I}{N_{0}}$ denoting fractions of the classes $P$, $S$, and $I$ in the constant population ${N_{0}}$, and satisfying $v+s+i = 1$:

Due to invertibility of the transformation used, the two systems are equivalent, and the scaled model (2.2) inherits all the properties of the original model (2.1), including existence and stability of a disease-free equilibrium (DFE) $(v^{*}, s^{*}, 0) = \left(\frac{P^*}{N_0}, \frac{S^*}{N_0}, 0\right)$ and any endemic equilibria (EE) $(v^{**}, s^{**}, i^{**}) = \left(\frac{P^{**}}{N_0}, \frac{S^{**}}{N_0}, \frac{I^{**}}{N_0}\right)$.

2.1.   Partnerships

Partnerships play an important role in disease transmission of HIV. Here we consider both casual and long-term partnerships ^[19]. A casual partnership constitutes a single instance of a sexual encounter, whereas a long-term partnership consists of repeated sexual acts between the same two individuals over a longer period of time $\tau$, that represents the average long-term partnership duration. The following cases will be described and analyzed:

● Case I: Casual-only partnerships: susceptible individual of interest, X, is not in any long-term partnership but engages only in casual sexual behavior.

● Case II: Monogamous long-term partnerships: susceptible individual of interest, X, is in a monogamous long-term partnership with infected individual Y. The individual X does not engage in any casual sexual behavior outside of this partnership.

● Case Ⅲ: Non-monogamous long-term partnerships: susceptible individual of interest, X, is in a long-term partnership with infected individual Y but at the same time X may have a casual sexual encounter with another infected individual, outside of the long-term partnership.

We assume that all individuals mix randomly with constant casual and long-term partner acquisition rates. Additionally, all sexual encounters are independent of each other and since all considered partnerships are serodiscordant, no transitive transmission of infection can ever take place, meaning that the susceptible individual of interest cannot become infected due to his long-term partner's involvement in a casual partnership with another infected individual. The case of concurrent partnerships among two susceptible individuals, which would allow for transitive infectivity, is our ultimate goal and will be a subject of our future work. We further assume that the risk factors are fixed across time and do not differ among the individuals, meaning that no susceptible person has a higher chance of contracting HIV than others within the same group, at any given time. The parameters pertaining to the above cases, based on the type of partnership considered, are listed in Table 2.

A widely-studied approach of studying sexually transmitted diseases is a pair-formation model ^{[17,21,22,23]}. It captures the complex dynamics of partnership duration and infection duration but requires explicit description of every combination of characteristics within pairs. This quickly increases the number of differential equations needed to describe the dynamics. Another limitation of pair formation models is that concurrent partnerships can only be added using moment closure methods. Our goal is to overcome these limitations and propose a novel approach. In ^[19], we compared two pair formation models with a long-term partnership model. Numerical simulations showed that the long-term partnership model without concurrency (transitive infections) mimics the pair formation models. We also concluded that the corresponding reproduction numbers are comparable, and the overall dynamics of these models are almost identical, even with the low concurrency rate. A significant advantage of the long-term partnership model is that having fewer equations allows for analytic calculations in addition to numerical simulations.

2.2.   Case I: $PSI$ model with casual-only partnerships

In this case, the susceptible individual X does not have any long-term partners but engages in casual sexual acts. The infection rate from casual partners, denoted $\lambda_{z}$, follows the classic law of mass action with a zero inherent length infection contact. It assumes that the transmission rate from an infected individual in $I$ is $z \beta$, where $z$ is the rate of casual sexual encounters and $\beta$ is the transmission probability per sexual encounter with an infected individual, and is calculated as

The reproduction number is calculated using the next generation method ^[24]. In the absence of PrEP (i.e., $\sigma = \theta = \alpha = 0$), the basic reproduction number is $R_0^z = \dfrac{z \beta}{\mu}$. When PrEP is present, we obtain the threshold parameter, often referred to as a 'vaccine' reproduction number,

We use subscript $\theta$ to emphasize the role of the PrEP treatment uptake, $\theta$, in controlling the spread of the disease, and a superscript $z$ to indicate the reproduction number was calculated for the casual partnerships. It is worth noting that $R_\theta^z \leq R_0^z$. Using standard procedure we calculate the disease-free equilibrium

and, with help of Mathematica, the endemic equilibrium:

Since the effectiveness of PrEP, $r$, is approximately $95\%$ ^[3] and it is unlikely we get adherence to daily dosages, $q$, to be $100\%$, we assume that $qr\neq 1$. The unlikely case of $qr = 1$ would correspond to having a perfect vaccine.

2.2.1.   Stability of the equilibria

Before proving stability, we will show the existence and uniqueness of equilibria when $R^z > 1$. Substituting $s = 1-v-i$ into the last two equations in (2.2), gives a reduced system

It is straightforward to check that $(0, v^{*})$ from (2.5) is always a disease-free equilibrium of (2.7). The positive (endemic) equilibria in the interior of $D$ are determined by equations:

We begin our investigation of endemic equilibria for model (2.7) by considering two extreme special cases. First, suppose that $1-qr = 1$, i.e., the PrEP treatment is completely ineffective. Recall that $q$ is the level of adherence to PrEP treatment and $r$ is PrEP effectiveness, thus $qr = 0$. This reduces $R^z$ to $R_0^z = \frac{z \beta}{\mu}$. Now, with $R_0^z > 1$, $i$ asymptotically approaches $\left(1-\frac{1}{R_0^z}\right)$ and, consequently, $v$, the fraction of the population taking PrEP, approaches $\frac{\mu \alpha+\theta \frac{1}{R_0^z}}{\theta+\mu+\sigma+z \beta \left(1-\frac{1}{R_0^z}\right)}$. Here we observe the classical threshold behavior of the basic reproduction number. If instead, we suppose that $1-qr = 0$, so that the PrEP is completely effective and with full adherence, then we find one (stable) endemic equilibrium, which also exists only for $R^z > 1$.

Now we want to address the existence of endemic equilibria for $0 < 1-qr < 1$. Eliminating $v$ from the system (2.8) gives: $h(i):= Ai^{2}+Bi+C = 0$, where

Note that $h(0) = C$, $h(1) = A+B+C = -\mu[1-qr(1-\alpha)]-\frac{\mu}{z \beta} (\sigma + \mu + \theta) < 0$, and that $h$'s vertex lies to the left of $i = 1$ ($i = 1$ means that the entire population is infected) at $i = -\frac{B}{2A} < \frac{z \beta (1-qr)}{2 z \beta (1-qr)} = \frac{1}{2}$. Since an endemic equilibrium corresponds to a solution of $h(i) = 0$ on the unit interval $[0, 1]$, by examining the quadratic $h$, we can see that when $R^z > 1$ there is exactly one such $i$, indicating that there is a unique endemic equilibrium $(i^{**}, v^{**})$, as in (2.6) whenever $R^z > 1$.

We now look at the case when $R^z < 1$, which means $C < 0$. If at the same time $B < 0$ then the quadratic function has no real roots. Therefore we are left with the last case, namely $B > 0$ (i.e., $0 < -\frac{B}{2A} = \frac{1}{2}-\frac{(\mu+\theta)(1-qr)+(\mu+\sigma)}{2 z \beta(1-qr)} < \frac{1}{2}$, and abscissa of a vertex is $0 < i < 1$) and $B^2 -4AC > 0$ (i.e., $h(i)$ has two real zeros), which, together with $C < 0$, would guarantee two real solutions of $h(i) = 0$ on the unit interval $[0, 1]$. The condition $B^2 -4AC > 0$ is quadratic, but can be simplified using the condition $B > 0$. The two conditions cannot, however, be reduced to one, but can be written in terms of $z \beta$, which is linearly correlated with $R^z$. The condition $B > 0$ is satisfied when $z \beta > \mu + \theta + \dfrac{\mu+\sigma}{1-qr}$, while $B^2 -4AC > 0$ requires

Notice that as $R^z \rightarrow 1^-$, the square root in (2.10) heads to $0^+$. Using parameter values in Table 2, we see that $z \beta \approx 0.0548$, $\mu +\theta +\dfrac{\mu +\sigma}{1-qr} > 0.0428+\theta$, and, when $R^z < 1$, $qr > 0.7$, which collectively forces $\theta$ to be negative in order to satisfy condition (2.10). Therefore, we have just shown the following result.

Theorem 2.1. For the system $(2.7)$, with $R^z$ as defined previously,

1) When $R^z > 1$, there exists a unique endemic equilibrium $(i^{**}, v^{**})$.

2) When $R^z < 1$, there does not exist any endemic equilibrium.

The local stability of the DFE is analyzed using the eigenvalues of the Jacobian for the model (2.2) with the rate of infection (2.3). The three real eigenvalues are $\lambda_{1} = - \mu$, $\lambda_{2} = - (\mu +\theta + \sigma)$, and $\lambda_{3} = - \mu + z \beta \left[1- \dfrac{qr(\theta+\mu \alpha)}{\sigma +\mu +\theta}\right]$, with the first two always being negative and the third one being negative only when $\mu > z \beta \left[1- \dfrac{qr(\theta+\mu \alpha)}{\sigma +\mu +\theta}\right] = \mu R^z$. We conclude the classic result of DFE being locally stable when $R^z = \dfrac{z \beta}{\mu} \left[1- \dfrac{qr(\theta+\mu \alpha)}{\sigma +\mu +\theta}\right] < 1$ and unstable when $R^z > 1$. To prove the global stability we will use the method of Lyapunov functions but first we will state and prove few necessary and helpful results.

Lemma 2.2. The closed set $D = \lbrace (v, s, i)\in {\mathbb R}_{+}^{3} : 0 \leq v+s+i \leq 1 \rbrace$ is positively invariant with respect to model $(2.2)$.

Proof. Define $x = v+s+i$. It follows from the model (2.2) that $\dfrac{dx}{dt} = \mu - \mu x,$ which gives $x(t) = 1 - (1-x(0)) e^{-\mu t}$. Thus, $0 \leq x(t) \leq 1$ for all values of $t > 0$, if $0 \leq x(0) \leq 1$ (i.e. $x(t) \in D$ for all $t > 0$ if $x(0) \in D$). Hence, $D$ is positively invariant.

Lemma 2.3. Suppose $x_{1}, \ldots, x_{n} > 0$ and $\prod_{j = 1}^{n} x_{j} = 1$. Then

Proof. Consider the Volterra function $g(x) = x-1- \ln x$, with $g(x) \geq 0$ for all $x > 0$.

Note that

Then

Corollary 2.4. Let $(v, s, i), (\hat{v}, \hat{s}, \hat{i}) \in D$. Since $\dfrac{\hat{v}}{v} \cdot \dfrac{v}{\hat{v}} = \dfrac{\hat{s}}{s} \cdot \dfrac{s}{\hat{s}} = \dfrac{\hat{v}}{v} \cdot \dfrac{s}{\hat{s}} \cdot \dfrac{v\hat{s}}{s\hat{v}} = 1$, by Lemma 2.3,

Lemma 2.5. Given $(v, s, i), (\hat{v}, \hat{s}, \hat{i}) \in D$ such that $v+s+i = \hat{v} +\hat{s} +\hat{i}$, we have $(v-\hat{v})(s-\hat{s}) \leq 0$

Proof. We can write $(s-\hat{s}) = (\hat{v}-v)+(\hat{i}-i)$ and $(\hat{s}-s) = (v-\hat{v})+(i-\hat{i})$, then consider two cases.

If $i > \hat{i}$ then $(s-\hat{s}) < (\hat{v}-v)$ and $(v-\hat{v})(s-\hat{s}) \leq (v-\hat{v})(\hat{v}-v) = - (v-\hat{v})^2 \leq 0$.

If $i < \hat{i}$ then $(\hat{s}-s) < (v-\hat{v})$ and $(v-\hat{v})(s-\hat{s}) = -(v-\hat{v})(\hat{s}-s)\leq -(v-\hat{v})^2 \leq 0$.

Theorem 2.6. The DFE of the transformed model $(2.2)$, given by $(v^{*}, s^{*}, 0)$ in (2.5), is globally asymptotically stable in $D$ whenever $R^z \leq 1$ and $qr \neq 1$.

Proof. Define the nonlinear Lyapunov function of Goh-Volterra type ^[25,26]

with Lyapunov derivative given by

where a dot represents differentiation with respect to time. Substituting model (2.2) gives

After extensive simplifying, using the facts that $\mu(1-\alpha) + \sigma v^{*} - (\theta + \mu) s^{*} = 0$ and $\mu \alpha +\theta s^*- (\sigma +\mu) v^{*} = 0$, obtained from evaluating the equilibrium equations at $DFE$, we get

Now, considering that $i > i^* = 0$, using Lemma 2.5 together with the identity $s^{*} + (1- qr) p^{*} = 1 - \dfrac{qr(\theta+\mu \alpha)}{\sigma +\mu +\theta}$, we can write

Using the results from the Corollary 2.4 we can finally conclude that $\mathcal{\dot {L}} \leq 0$ when $R^z \leq 1$. Thus, by Lyapunov stability theorem, and LaSalle's Invariance Principle, every solution (in $D$) to the equations of the transformed model (2.2) approaches the DFE as $t\rightarrow \infty$ for $R^z \leq 1$ and $qr \neq 1$.

It follows that the use of PrEP will lead to the elimination of the disease from the community whenever $R^z \leq 1$ and $qr \neq 1$.

Theorem 2.7. The unique EE of the model $(2.2)$, given by $(v^{**}, s^{**}, i^{**})$ in $(2.6)$, is globally asymptotically stable in $D$ whenever $R^{z} > 1$ and $qr \neq 1$.

Proof. Define the non-linear Lyapunov function of Goh-Volterra type ^[25,26] (similar to the proof of Theorem 2.6)

The proof here follows the same ideas as in the proof of Theorem 2.6, where we show $\mathcal{\dot {M}} \leq 0$ using the model (2.2), identities obtained from evaluating the equilibrium equations at EE, and the results of the Corollary 2.4 and the Lemma 2.5.

Hence, by Lyapunov stability theorem, and LaSalle's Invariance Principle, every solution (in $D$) to the equations of the transformed model (2.2) approaches the unique EE as $t\rightarrow \infty$ for $R^{z} > 1$ (and $qr \neq 1$).

As evidenced above, the equilibria of the model (2.2) collide and exchange the stability when $R^z = 1$, meaning the (transcritical) bifurcation occurs at $R^z = 1$. Under certain conditions, to be determined below, this could potentially become a 'backward' (subcritical) bifurcation, which would mean the endemic equilibria exist for $R^z < 1$ as well as for $R^z > 1$. In that case, there would be some critical value of $R^z$ below $1$, where a pair of endemic equilibria would be created at a second, saddle-node type bifurcation point. We would find this bifurcation point for $R^z$, by solving $B^2-4AC = 0$ ^[27], obtained earlier using (2.9). Recalling that $C = \dfrac{\mu}{z \beta}(\mu+\theta+\sigma)(R^z -1)$, the equation $B^2-4AC = 0$ would become

which similarly to (2.10) cannot be satisfied without forcing $\theta$ to be negative.

Using the same technique as before, we could also try to identify the bifurcation point in terms of $z \beta$ by rewriting $B^2-4AC = 0$ as

However the conclusion would still be the same, namely, with feasible values of the parameters present in the model, there is no backward bifurcation and the unique endemic equilibrium exists only when $R^z > 1$.

2.3.   Case II: $PSI$ model with monogamous long-term partnerships

This case assumes that both the susceptible individual X and his infected long-term partner Y are exclusive with each other and do not engage in any sexual acts outside of their partnership. Since there are no casual sexual acts, the susceptible can only become infected through the infected long-term partner at a rate $\lambda_p$. We assume that the rate of transmission of infection within a long-term partnership with an infected individual in $I$ is $\chi$. The probability of transmission per partner depends upon the average number of contacts per partner and the mean probability of transmission per contact. Just as with the casual sexual partnership, the infected partner in $I$ can possibly infect the susceptible partner in a single sexual act, at a probability of $\beta$. In the case of long-term partnerships with infected individual, we assume that the partners mitigate the infection risk with condoms approximately $85\%$ of the time (see parameter $c_u$ in Table 2). However, the probability of an individual being fully protected also depends on the condom effectiveness $c_{eff}$ and is hence equal to $c_{eff}\cdot c_u$. If we define the reduction factor due to condom effectiveness and usage as $c = 1-c_{eff}\cdot c_u$, then the term $c \beta$ is the transmission probability per sexual contact. Consequently, the probability of not being infected in a single act is $(1- c \beta)$, and the probability of not being infected after $n$ sexual acts is $(1- c \beta)^{n}$. Here, the exponent $n = 104\tau$ reflects the number of sexual contacts over the duration of long-term partnership $\tau = 1/(b+ 2 \mu)$, with $\mu$ being the population removal rate (by death or due to ceasing sexual activity) and $b$ denoting the rate at which long-term partnerships dissolve ^[28]. In $\lambda_z$ we used the average rate of having casual encounters per year, $z$. Similarly, in $\lambda_p$ we use the rate of acquiring long-term partners per year, $p/\tau$. It is derived using the number of lifetime long-term partners $M = f/(\mu(f \tau + 1))$, defined for pair formation model by ^[19,22], where $f$ is the pair formation rate, $\tau$ is the partnership duration, and $1/\mu$ is the lifetime. Thus, the number of long-term partners per year becomes $M \mu = f/(1+f \tau)$, which is our definition for $p/\tau$. Following Kretzschmar and Heijne ^[22], parameter $p$ is a fraction of population in a long-term partnership but also describes the fraction of his lifetime that an individual is cumulatively in long-term partnerships. Therefore, the probability that the susceptible long-term partner will be infected after $n$ sexual acts with the long-term partner in $I$ is our rate of transmission $\chi = (p/\tau) \left(1- (1-c \beta)^{n} \right)$.

When deriving the rate of infection $\lambda_{p}$ from an infected partner, we assume that the infected partner has not transmitted the infection before a given time $t$. In short, the rate of infection by the fraction of infected long-term partners out of the total population is the expected value of the rate of infection due to partners initially chosen while infectious,

The probability that an infected partner, who is acquired at time $\kappa$, transmits the infection at a later time $t$, is given by the product of the following probabilities, multiplied by the rate of transmission $\chi$:

$1)$ The probability that a partner acquired at time $\kappa$ was already infected: $P(X(\kappa) \in I) = i(\kappa)$.

$2)$ The probability that a partner acquired at time $\kappa$ will still be a partner at time $t$: $P(X(t) \in Partner)$.

In our calculation, we use the definition of the expected value of a continuous random variable $X$ with range $[a, b]$ and probability distribution function $g(x)$,

We can interpret the formula for $E[X]$ as a weighted integral of the values $x$ of random variable $X$, where the weights are the probabilities $g(x)dx$. We assume that the probability (see item 2.3 above) of the partnership lasting through time $t$ can be described by a distribution function that is a decaying exponential scaled by the length of an average long-term partnership, $\tau$,

With that in mind, and remembering that $\kappa \in [- \infty, t]$, our expected value of the rate of infection is

Since we are dealing with a nonlinear and a non-local problem, it is not feasible to keep track of the number of infected individuals for all time prior to the instant $t$ at which the infection occurs. To make the calculations tractable, we will define $\lambda_{p}$ to be a linear approximation to the expected value, with $i(\kappa) \approx i(t) + i'(t)(\kappa - t)$, and $i'(t) = \lambda s(t) + (1-qr) \lambda v(t)- \mu i(t)$ directly from our ODE model (2.2), giving us

in the integrand of (2.11). In other words, we are approximating the fraction of infectious individuals $i(\kappa)$ at time $\kappa$ as the fraction of infected at time $t$ plus the fraction of infected who died $(1+ \mu \tau)i(t)$ and subtracting off the fraction of the individuals $\lambda \tau (s(t) + (1-qr) v(t))$ who became infected between times $\kappa$, when the long-term relationship began, and the current time $t$ with $\tau = t- \kappa$.

Therefore

Then the rate of infection from the infected long-term partner is

Solving the above equation explicitly for $\lambda$, we get:

As in Case Ⅰ (Section 2.2), the reproduction number is calculated using the next generation method. In the absence of PrEP (i.e., $\sigma = \theta = \alpha = 0$) we get the basic reproduction number, $R_0^p = \frac{\chi(1+\mu \tau)}{\mu(1+\chi \tau)}$. When PrEP is present, we once again obtain the so-called threshold parameter, aka.'vaccine' reproduction number,

which only makes sense (i.e., is positive) when $\sigma +\mu+\theta > qr(\theta+\mu \alpha)$. It is also straightforward to check that $R^p < 1+\frac{1}{\mu \tau}$.

The disease-free equilibrium is once again calculated to be

and, with help of Mathematica, the endemic equilibrium is

2.3.1.   Global stability of equilibria

Before we prove global stability of both equilibria we will examine the existence and uniqueness of the EE. It is again convenient to work with the simplified system, as in (2.7), but now with the rate of infection from (2.12)

It is straightforward to check that $(0, v^{*})$ from (2.14) is always a disease-free equilibrium of (2.16). The positive (endemic) equilibria in the interior of $D$ are determined by setting the right-hand sides of model (2.16) to 0 and simplifying to

Note that in order for the above to make sense we must have $\mu < \chi$, that is, the rate of population removal is less than the transmission rate from an infected long-term partner, which is always the case with our parameter values.

We begin our investigation of endemic equilibria for model (2.16) by considering two extreme special cases. First, suppose that $1-qr = 1$, i.e., the PrEP treatment is completely ineffective. This reduces $R^p$ to $R_0^p = \frac{\chi(1+\mu \tau)}{\mu(1+\chi \tau)}$. Now, if $R_0^p > 1$, then $\mu < \chi$, and $i$ approaches $\left(1-\dfrac{\mu}{\chi}\right)$ while $v$ approaches $\dfrac{\mu (\chi \alpha+\theta)}{\chi(\theta+\chi+\sigma)}$. Here we observe classical $R_0^p$ threshold behavior since endemic equilibrium does not exist if $R_0^p < 1$ (i.e., $\mu > \chi$). If instead, we suppose that $1-qr = 0$, meaning the PrEP is completely effective and with full adherence, then we find one (stable) endemic equilibrium, which exists only for $R^p > 1$:

Now we want to address the existence of endemic equilibria for $0 < 1-qr < 1$, in the realistic realm of imperfect PrEP adherence and effectiveness. Eliminating $v$ from the system (2.17) gives: $h(i):= Ai^{2}+Bi+C = 0$ where

Using series of algebraic manipulations we obtain the following helpful result.

Lemma 2.8. Given $R^p$ and $C$ as stated before, we can write $R^p -1 = \dfrac{C}{\mu [C \tau + (1+\mu \tau)(\theta+\mu+\sigma)]}$ or, equivalently, $C = \dfrac{\mu (1+\mu \tau)(\theta+\mu+\sigma)}{\frac{1}{R^p-1}-\mu \tau}$, and deduce that when ($R^p < 1$) then $C < 0$, and if $1 < R^p < 1+\frac{1}{\mu \tau}$ then $C > 0$.

The rest of the analysis is summarized in the theorem below.

Theorem 2.9. For the system $(2.16)$, with $0 < 1-qr < 1$ and $R^p$ as defined in $(2.13)$,

1) When $1 < R^p < 1+\frac{1}{\mu \tau}$., there exists a unique endemic equilibrium $(i^{**}, v^{**})$.

2) When $R^p < 1$, there does not exist any endemic equilibrium.

Proof. We start with part 1, namely the case of $1 < R^p < 1+\frac{1}{\mu \tau}$. By Lemma 2.8, $C > 0$ which, together with $A < 0$, gives $B^2-4AC > 0$. Recalling that $h(1) < 0$, we can conclude that $h$ has exactly one zero in $(0, 1)$ and therefore the system (2.16) has a unique EE when $1 < R^p < 1+\frac{1}{\mu \tau}$.

To prove part 2, we consider $R^p < 1$, and note that, from Lemma 2.8, $h(0) = C < 0$ and $h(1) = A+B+C = -\mu[\chi(1-qr)+\chi qr \alpha +\theta+\sigma+\mu] < 0$. If, in addition, we assume $\theta > \chi - \mu$, which with our parameters, translates to PrEP uptake rate $\theta$ of more that $7.2\%$, then $B < 0$. In that case it follows that $h$'s vertex at $i = -\frac{B}{2A} = -\dfrac{1}{2} \dfrac{\mu+\sigma+(\theta-\chi+\mu)(1-qr)}{\chi(1-qr)} < 0$ lies to the left of $i = 0$. Since an endemic equilibrium corresponds to a solution of $h(i) = 0$ on the unit interval $[0, 1]$, by examining the quadratic $h$, we can see that there is no such $i$. If, alternatively, we consider $\theta < \chi - \mu$, but keep $1-qr < -\frac{\mu + \sigma}{\theta-\chi+\mu}$, which with our parameters and advertised PrEP effectiveness would call for treatment adherence $q$ of at least $70\%$, then we still have vertex of $h$ to the left of $i = 0$, and hence no possible zeros in the interval $(0, 1)$.

Now we look at the case when $A < 0, \; C < 0, \; B > 0$ (i.e., $0 < -\frac{B}{2A} < \frac{1}{2}$ since $\frac{B}{A} = \frac{\mu+\sigma+(\theta+\mu)(1-qr)}{\chi(1-qr)}-1 > -1$) and $B^2 -4AC\geq0$, which would collectively indicate real solutions of $h(i) = 0$ on the unit interval $(0, 1)$ when $R^p < 1$. The condition $B^2 -4AC\geq0$ is quadratic, but can be simplified using the condition $B > 0$. The two conditions cannot, however, be reduced to one, but can be written in terms of $\chi$, which is linearly correlated with $R^p$. The condition $B > 0$ is satisfied when $\chi > \mu + \theta + \dfrac{\mu+\sigma}{1-qr}$ while $B^2 -4AC\geq0$, simplified using Lemma 2.8, requires

Notice that as $R^p \rightarrow 1^-$, the square root in (2.20) heads to $0^+$. Using parameter values in Table 2, we see that $\chi \approx 0.0883$ and $0.0428+\theta < \mu +\theta +\dfrac{\mu +\sigma}{1-qr} < 0.1553+\theta$, depending on $q$. With all that in mind, combined with the relationship in Lemma 2.8, we can conclude that even undesirably low adherence rate of $50 \%$ would force $\theta$ to be negative, in order for the condition (2.20) to be satisfied. Hence, we can now conclude that there is no endemic equilibrium $(i^{**}, v^{**})$, whenever $R^p < 1$.

The global stability proofs are very similar to the previous case with casual partnerships and hence we will omit some steps.

Theorem 2.10. The DFE of the transformed model $(2.2)$, given by $(v^{*}, s^{*}, 0)$ in (2.14), is globally asymptotically stable in $D$ whenever $R^p \leq 1$ and $qr \neq 1$.

Proof. Once again, define the nonlinear Lyapunov function of Goh-Volterra type ^[25,26]

with Lyapunov derivative $\mathcal{\dot {L}}$. Substituting model (2.2), as well as using the facts that $\mu(1-\alpha) + \sigma v^{*} - (\theta + \mu) s^{*} = 0$ and $\mu \alpha +\theta s^*- (\sigma +\mu) v^{*} = 0$, while rewriting the reproduction number (2.13) as $R^p = \dfrac{\chi(1+\mu \tau)[s^*+(1-qr)v^*]}{\mu[1+\chi \tau [s^*+(1-qr)v^*]]}$, we obtain

Finally, noticing that the rate of infection cannot be greater than the fraction of those infected (i.e. transmission factor $\frac{\chi (1+\mu \tau)i}{1+\chi \tau (s+(1-qr)v)}\leq 1$) and recalling that $\chi > \mu$, we can write

Since $R^p \leq 1$, using the results in Corollary 2.4 we can finally conclude that $\mathcal{\dot {L}} \leq 0$. Thus, by Lyapunov stability theorem, and LaSalle's Invariance Principle, every solution (in $D$) to the equations of the transformed model (2.2) approaches the DFE as $t\rightarrow \infty$ for $R^p \leq 1$ and $qr \neq 1$.

It follows that the use of PrEP will lead to the elimination of disease from the population, with presence of only long-term partnerships with infected partners, whenever $R^p \leq 1$ and $qr \neq 1$.

Theorem 2.11. The unique EE of the transformed model $(2.2)$, given by $(v^{**}, s^{**}, i^{**})$ in $(2.15)$, is globally asymptotically stable in $D$ whenever $R^{p} > 1$ and $qr \neq 1$.

Proof. The proof here is analogous to the proof of Theorem 2.7 in the casual-only case, but with rate of infection (2.12), where we define the non-linear Lyapunov function of Goh-Volterra type

and show $\mathcal{\dot {M}} \leq 0$.

As evidenced above, when $R^p = 1$ the equilibria collide and their stability is exchanged, which means that our model has the usual (transcritical) bifurcation at $R^p = 1$. Under certain conditions, to be determined below, this could potentially become a "backward" (subcritical) bifurcation, which would mean the endemic equilibria exist for $R^p < 1$ as well as for $R^p > 1$. In that case there would be some critical value of $R^p$ below $1$, where a pair of endemic equilibria would be created at a second, saddle-node type bifurcation. We would find this bifurcation point by solving $B^2-4AC = 0$ ^[27] (using expressions in (2.19)) for $R^p$. Using Lemma 2.8 and (2.19) we can write the equation $B^2-4AC = 0$ as

which, together with $R^p < 1$, would require $B^2 \mu \tau < 4\mu (1-qr)(1+\mu \tau)(\mu+\theta+\sigma)$. With the parameters in Tables 1 and 2 the above condition cannot be satisfied without forcing $\theta$ to be negative. Our conclusion is that with feasible values of the parameters present in the model, there is no backward bifurcation and the unique endemic equilibrium exists only when $1 < R^p < 1+\frac{1}{\mu \tau}$.

2.4.   Case Ⅲ: $PSI$ model with non-monogamous long-term partnerships

This case assumes that the susceptible individual of interest, X, is in a long-term partnership with infected individual, Y, but at the same time X may have a casual sexual encounter with another infected individual, outside of the long-term partnership. In essence, this is a combination of the casual only and the monogamous long-term cases of our model (2.1). It is important to note that the occurrence of infection transmission from an infected casual partner is independent of the transmission from an infected long-term partner, so the probability that a susceptible individual becomes infected is a sum of the probabilities of infection in both cases. Therefore, we can describe the rate of infection, using previously calculated rates $\lambda_{z}$ ((2.3) in casual-only case) and $\lambda_{p}^{I}$ ((2.12) in monogamous long-term case), as

Solving the above equation explicitly for $\lambda$, we obtain the rate of infection for non-monogamous long-term case

Once again, the reproduction number is calculated using next generation method and expressed as

with $R_0 = \frac{z \beta + \chi (1+\mu \tau)}{\mu(1+\chi \tau)}$ being the basic reproduction number in the absence of PrEP. The disease-free equilibrium and endemic equilibrium are calculated, respectively, as

and

2.4.1.   Global stability of equilibria (with $qr \neq 1$)

Once again, before we prove global stability of both equilibria, we will examine the existence and uniqueness of EE, all using the simplified model equations

with the rate of infection $\lambda = \dfrac{[z \beta + \chi (1+ \mu \tau)]i}{1+ \chi \tau [s + (1-qr) v]}$ derived in (2.21).

It is straightforward to check that $(0, v^{*})$ from (2.23) is always a disease-free equilibrium of (2.25). The positive (endemic) equilibria in the interior of $D$ are determined by setting the right-hand sides of (2.25) to zero and simplifying to

Note that in order for the above to make sense we must have $\mu < z \beta+\chi$, which, as in earlier cases, is satisfied with our parameter values. Since this case is a combination of Case Ⅰ (Section 2.2) and Case Ⅱ (Section 2.3), the analysis of existence and stability of equilibria is very similar to the case with monogamous long-term partnerships. Therefore, we will state the main results while omitting some details in the calculations as well as in the proofs of the theorems.

Assuming $0 < 1-qr < 1$ and eliminating $v$ from (2.26) gives $h(i):= Ai^{2}+Bi+C = 0$, where

with $h(0) = C$ and $h(1) = A+B+C = -\mu[\chi(1-qr)+\chi qr \alpha +\theta+\sigma+\mu] < 0$. Thus the number of zeros of $h$ will depend on the signs of $C$ and the discriminant.

Lemma 2.12. We can write $R_{\theta} -1 = \dfrac{(z \beta+\chi)C}{\mu [C \chi \tau + (z \beta+\chi+\mu \chi \tau)(\theta+\mu+\sigma)]}$ or, equivalently, $C = - \dfrac{(z \beta+\chi+\mu \chi \tau)(\theta+\mu+\sigma)}{\mu \chi \tau+ \frac{z\beta+\chi}{1-R_{\theta}}}$ and deduce the following:

1) If $R_{\theta} < 1$ then $C < 0$ and if $1 < R_{\theta} < 1+\frac{z\beta+\chi}{\mu \chi \tau}$ then $C > 0$.

2) When $1 < R_{\theta} < 1+\frac{z\beta+\chi}{\mu \chi \tau}$ then $h(0) > 0$ and hence, by IVT, $h(i) = 0$ has exactly one real solution in $(0, 1)$.

3) When $R_{\theta} < 1$ and $z\beta+\chi < \theta+\mu$ then

● $h(0) < 0$ and $B < 0$,

● $h$'s vertex lies to the left of $i = 0$ since $-\frac{B}{2A} < 0$,

and hence $h(i) = 0$ has no real solutions in $(0, 1)$.

4) When $R_{\theta} < 1$ and $B > 0$ then

● $h(0) = C < 0, h(1) < 0$,

● $h$'s vertex lies to the left of $i = \frac{1}{2}$ since $\frac{B}{A} = \frac{\mu+\sigma+(\theta+\mu)(1-qr)}{(z\beta+\chi)(1-qr)}-1 > -1$ and $0 < -\frac{B}{2A} < \frac{1}{2}$, and hence $h(i) = 0$ will have real solutions in $(0, 1)$ only if $B^2 -4AC > 0$. However, $B^2 -4AC > 0$ requires $z\beta+\chi \geq \mu +\theta +\dfrac{\mu +\sigma}{1-qr}+ 2\sqrt{\dfrac{(\theta +\mu+\sigma)}{(1-qr)} \left(1-\dfrac{(z\beta+\chi)R_{\theta}}{z\beta+\chi+\mu \chi \tau (1-R_{\theta})}\right)}$, which cannot be satisfied with feasible values of parameters.

Now we can state the main results that follows from the above Lemma 2.12 as well as the stability proofs in previous cases.

Theorem 2.13. For the system $(2.25)$, with $R_{\theta}$ as defined previously,

1) When $1 < R_{\theta} < 1+\frac{z\beta+\chi}{\mu \chi \tau}$, there exists a unique endemic equilibrium $(i^{**}, v^{**})$.

2) When $R_{\theta} < 1$, there does not exist any endemic equilibrium.

Theorem 2.14. The DFE of the transformed model $(2.2)$, given by $(v^{*}, s^{*}, 0)$ in $(2.23)$, is globally asymptotically stable in $D$ whenever $R_{\theta} \leq 1$ and $qr \neq 1$.

Proof. Defining the non-linear Lyapunov function of Goh-Volterra type ^[25,26]

with corresponding Lyapunov derivative, after substituting model (2.2) and extensive simplifying, using the facts that $\mu(1-\alpha) + \sigma v^{*} - (\theta + \mu) s^{*} = 0$ and $\mu \alpha +\theta s^*- (\sigma +\mu) v^{*} = 0$, and rewriting the reproduction number (2.22) as $R_{\theta} = \dfrac{[z \beta+\chi(1+\mu \tau)][s^*+(1-qr)v^*]}{\mu[1+\chi \tau [s^*+(1-qr)v^*]]}$, we obtain

Then, noticing that the rate of infection cannot be greater than the fraction of infected individuals (i.e. transmission factor $\frac{[z \beta+\chi(1+\mu \tau)]}{1+\chi \tau (s+(1-qr)v)}\leq 1$) and recalling that $z\beta+\chi > \mu$, we can write

Since $1+\chi \tau (1-R_{\theta})\geq 1$, the last term can be further simplified to give

Using the results in Corollary 2.4 we can finally conclude that $\mathcal{\dot {L}} \leq 0$. Thus, by Lyapunov stability theorem, and LaSalle's Invariance Principle, every solution (in $D$) to the equations of the transformed model (2.2) approaches the DFE as $t\rightarrow \infty$ for $R_{\theta} \leq 1$ and $qr \neq 1$.

It follows that the use of PrEP will lead to the elimination of the disease from the population with both casual and long-term partnerships with infected partners whenever $R_{\theta} \leq 1$ and $qr \neq 1$.

Theorem 2.15. The unique EE of the transformed model $(2.2)$, given by $(v^{**}, s^{**}, i^{**})$ in $(2.24)$, is globally asymptotically stable in $D$ whenever $1 < R_{\theta} < 1+\frac{z\beta+\chi}{\mu \chi \tau}$ and $qr \neq 1$.

Proof. Once again, we define the non-linear Lyapunov function of Goh-Volterra type ^[25,26]

and follow the same steps as in the proofs of Theorems 2.7 and 2.11, to conclude that $\mathcal{\dot {M}} \leq 0$. Thus, by Lyapunov stability theorem, and LaSalle's Invariance Principle, every solution (in $D$) to the equations of the transformed model (2.2) approaches the unique EE as $t\rightarrow \infty$ for $R_{\theta} > 1$ (and $qr \neq 1$).

As shown in the previous cases, here we can also conclude that with feasible values of the parameters present in the model, we observe the usual (transcritical) bifurcation at $R_{\theta} = 1$, there is no backward bifurcation, and the unique endemic equilibrium exists only when $1 < R_{\theta} < 1+\frac{z\beta+\chi}{\mu \chi \tau}$.

3.   Results

In this section, we investigate the impact of PrEP in the reduction of HIV transmission in three cases, differed based on the types of partnerships involved. We assume that the total population is a constant $N_0$, with recruitment rate $\pi = \mu N_0$ and population removal rate $\mu = 1/61$, as stated in Table 1. The initial conditions (in 10,000) are given by $P(0) = 7, S(0) = 640, I(0) = 63$ ^[1,2]. We start our numerical simulations assuming that $\alpha = 0.1$, meaning that $10\%$ of the individuals entering the population are already using PrEP, and $10\%$ of the susceptible individuals start PrEP, that is $\theta = 0.1$, with the stopping rate of $1\%$, i.e., $\sigma = 0.01$. The remaining parameters, $N_{0}$ the total population, $\mu$ the population removal rate, $\pi$ the recruitment rate, $\alpha$ the fraction of the newly recruited PrEP users, $q$ the level of adherence to PrEP treatment, $r$ the effectiveness of PrEP, $z$ the average number of casual partners per year, $\beta$ the transmission rate per one sexual act, $\tau$ the mean duration of long-term partnership, $p/\tau$ the average number of long-term partners per year, $n$ the number of sexual acts over the duration of long-term partnership, $c$ the transmission rate adjustment factor due to condom use, and $\chi$ the transmission rate from the infected long-term partner per year take on the values listed in Tables 1 and 2.

3.1.   Time series

Figure 2 illustrates the disease progression in the three cases analyzed in earlier sections: only casual partnerships (Figure 2a, b); only long-term partnerships with infected individuals (Figure 2c, d); and lastly, the combination of both (Figure 2e, f). For each of the cases, we are plotting (bold curves) the fractions of population in the three groups over time (in years) to show the long-term effect of PrEP on the number of susceptible and infected individuals, with thin lines illustrating the steady states. Solid green "" represents susceptible PrEP users (P), dashed blue "" refers to susceptibles not using PrEP (S), and dotted red "" indicates infected (Ⅰ). It is important to note that the results are based on the average number of casual partners per year $z$, total number of long-term partners $p$, mean duration of long-term partnerships $\tau$, and other parameters with values as listed in Table 2.

We observe the similar behavior in all three cases, with the susceptible group $S$ (dashed blue curve) decreasing and the infected group $I$ (dotted red curve) increasing. However, when comparing the graphs in the right column, it is evident that the time to equilibration varies significantly, with the longest being when only casual partnerships are considered and the shortest when both casual and long-term are included. On the other hand, the equilibrium value of the fraction of infected individuals (indicated by the thin dotted red lines on every graph) is the lowest in the casual-only case and roughly $50-80\%$ higher in the long-term and combined cases, respectively. This confirms the importance of considering long-term partnerships, suggesting that when long-term partnerships with infected individuals are taken into account then the effect of PrEP on curbing the spread of the disease and lowering the number of infected individuals is not as strong as when only casual partnerships are included in the model.

Another interesting observation relates to the change in the behavior of curves around the 20–30 years mark. After the relatively fast incline, the fraction of individuals using PrEP (solid green curves) peaks around the 20–30 years mark, and then starts to decline at a much slower but steady rate. At the same time, the number of infected individuals grows at an approximately constant rate. This could indicate that even if the implemented strategies of dealing with the spread of HIV produce plausible results, they might not be sufficient for the future generations.

3.2.   Uncertainty and sensitivity analysis

Uncertainty and sensitivity analysis are necessary to explore the behavior of the epidemiological models because their structural complexity comes with a high degree of uncertainty in estimating the values of many of the input parameters. Uncertainty analysis may be used to assess the variability in the outcome variable that is due to the uncertainty in estimating the values of the input parameters. A sensitivity analysis can extend an uncertainty analysis by identifying which input parameters are important (due to their estimation uncertainty) in contributing to the prediction imprecision of the outcome variable.

3.2.1.   Normalized forward sensitivity (Elasticity) of $R$

Knowledge of the relative importance of the different factors responsible for transmission is useful to determine best control measures. Initially disease transmission is related to reproduction number $R$ and sensitivity predicts which parameters have a high impact on its value. The sensitivity index of $R$ with respect to a parameter $\omega$ is $\dfrac{\partial R}{\partial \omega}$. Another measure is the elasticity index (normalized sensitivity index) that measures the relative change of $R$ with respect to $\omega$, denoted by $\mathscr{F}^{R}_{\omega}$, and defined as

The sign of the elasticity index specifies whether $R$ increases (positive sign) or decreases (negative sign) with the parameter; whereas the magnitude determines the relative importance of the parameter. If $R$ is known explicitly, then the elasticity index for each parameter can be computed explicitly, and evaluated for a given set of parameters. The magnitude of the elasticity indices depends on these parameter values, which are often only estimates.

For our model, we will focus on control parameters: the number of casual partners, $z$, rate of starting PrEP, $\theta$, rate of stopping PrEP, $\sigma$, level of adherence to PrEP regime, $q$, average number of long-term partners per year times the mean duration of long-term partnership, $p$, and the mean duration of long-term partnership, $\tau$. We use previously calculated expressions for the reproduction number $R$ in each of the three cases, as well as the values of parameters given in Table 2 as our baseline parameter values to obtain and present the results in Figure 3. Figure 3 displays the values of the normalized sensitivity indices in all three cases, for the aforementioned control parameters, and calculated assuming the baseline values listed in the Table 2, with $\theta = 0.1$ and $\sigma = 0.01$ (Figures 3a to 3c), while in Figures 3d to 3f the PrEP uptake and default rates were increased to $\theta = 0.6$ and $\sigma = 0.3$, respectively. Each index value can be thought of as a ratio of the effective change in the reproduction number with respect to the applied change in the given parameter. For example, when we look at Case Ⅲ in Figure 3c, for every $10\%$ increase in the fraction of population in long-term partnerships, $p$, the reproduction number will increase by $5.13\%$. However, it will decrease by $8.67\%$ for every $10\%$ increase in the PrEP use adherence, $q$.

We observe that in the case with only casual partnerships (Figure 3a, d), the reproduction number $R$ is very sensitive to changes in the average number of casual partners per year, $z$. However, once long-term partnerships are considered (Figure 3(b, c, e, f)), then the portion of individuals in long-term partnerships, $p$, has similar impact on the reproduction number.

When looking at all three cases, it is important to point out the commonality and significance of the difference in the impact that both PrEP uptake rate, $\theta$, and the adherence to the PrEP treatment, $q$, have on the value of $R$. The high magnitude of $q$ and very low magnitude of $\theta$ in Figures 3a to 3c might suggest that enforcing strict regime of the daily medication among those already in treatment could potentially slow down the disease progression faster than increasing the number of new PrEP users without perfect adherence. However, in Figures 3d to 3f, where we increased the PrEP uptake and default rates to $\theta = 0.6$ and $\sigma = 0.3$, respectively, we notice decrease in the magnitude of $q$, possibly indicating lower impact of adherence once the uptake rate is high enough.

3.2.2.   Global uncertainty analysis

In the deterministic model, the output is completely determined by the input parameters and structure of the model. The same input will produce the same output if the model were simulated multiple times. Therefore, the only uncertainty affecting the output is generated by input variation. Input factors for most mathematical models consist of parameters and initial conditions for independent and dependent model variables. These, however, are not always known with a sufficient degree of certainty because of natural variation, error in measurements, or simply a lack of current techniques to measure them. The purpose of uncertainty analysis is to quantify the degree of confidence in the existing experimental data and parameter estimates ^[29]. To consider the implications of our model in a more comprehensive manner, in this section we conduct global uncertainty and sensitivity analysis through Latin Hypercube Sampling (LHS) and Partial Rank Correlation Coefficients (PRCC). This enables a better understanding of the effects of parameter values on the amplification patterns we observe across our model simulations. In our analysis we include 6 model parameters and assign a uniform probability density function (pdf) to each. PRCC is usually the first step in assessing the global sensitivity of a model on the uncertainties in its parameters. The local analysis (done mainly through calculating/approximating the derivatives with respect to the parameters), such as the normalized forward sensitivity discussed earlier, provides direct information on the effect of small parameter perturbations about their nominal values, but it does not indicate the effect of concurrent, large perturbations in all model parameters (in bio-mathematics that is almost always the case). In order to calculate PRCC we simulate exactly those simultaneous large perturbations in model parameters. The PRCC provides good insight on global sensitivity, that is which parameters are most influential even if other parameters are simultaneously perturbed ^[30].

Figure 4 displays the results of PRCC analysis, where we mainly consider the parameters with PRCC values $> 0.5$ (for direct relation) or $< -0.5$ (for inverse relation) and with corresponding small p-values ($< 0.05$) as the most influential parameters for the model. The closer the PRCC value is to $\pm 1$, the more strongly the LHS parameter influences the outcome measure. The sign indicates the qualitative relationship between the input variable and the output variable. A negative sign indicates that the LHS parameter is inversely proportional to the outcome measure (fraction of infected individuals $i$ in our case). From the plots we could conclude that in our model, parameter $q$, the level of adherence to PrEP treatment, is a very likely contributor to uncertainty (PRCC values: $0.7$ to $0.79$ or $-0.7$ to $-0.79$) but it is the parameters $z$, the average number of casual partners per year, $p$, the average number of long-term partners per year times the mean duration of long-term partnership, and $\theta$, the rate of starting PrEP, that have the most important influence on the model as a whole (PRCC values: $0.8$ to $0.99$ or $-0.8$ to $-0.99$). The small p-values associated with them indicate that they are highly significant in the prediction of disease dynamics.

3.3.   PrEP uptake and adherence

Sensitivity analysis revealed the degree to which each parameter affects our model. We saw that the level of adherence $q$ to a daily regime of PrEP medication (assumed to be $90\%$ effective) and the rate $\theta$ of starting the treatment both have a significant impact on the HIV transmission dynamics. Figure 5 shows the impact of these two parameters on the value of the reproduction number $R$ in each of the three partnership scenarios, when all remaining parameters remain unchanged, with values as in Tables 1 and 2. The thicker contour line on some of the plots denotes the threshold value of reproduction number, i.e., $R = 1$. Absence of such line means that the threshold value cannot be reached with the given parameter values. We observe that when only casual partnerships are considered (Figure 5a) then regardless of the rate of starting PrEP, we can always pinpoint the rate of compliance needed to reach $R < 1$, and eventually (as seen in time series plots in Figure 2) eliminate the disease. In a population with only monogamous long-term partnerships (Figure 5b), the $10\%$ PrEP uptake rate is not enough to lower the reproduction number to $1$, regardless of the patients' compliance level. However, once we increase $\theta$ to at least $40\%$, then, as long as the adherence is near perfect (above $95\%$), the model will eventually approach the disease-free equilibrium. Lastly, when we look at the case with both casual and long-term partnerships (Figure 5c), we notice that even with maximum values of $\theta$, the rate of starting PreP, and $q$, the level of adherence, (both set to $99\%$) we cannot lower the reproduction number below unity, if the remaining parameters stay at the baseline values listed in Tables 1 and 2. In Figure 6 we explore the impact of changes in two parameters ($\alpha$, the fraction of the newly recruited PrEP users, and $r$, the effectiveness of PrEP) on the value of the reproduction number. Figure 6a shows that if all individuals enter population as PrEP users ($\alpha = 0.99$), then even perfect adherence to $90\%$ effective PrEP treatment would not be enough to eventually bring down the number of infections to $0$. However, if the effectiveness of PrEP was $95\%$ (Figure 6b) or $99\%$ (Figure 6c), then, with high enough level of compliance to the treatment, it would be possible to reach $R = 1$ at any PrEP uptake rate above $\theta = 0.45$ and $\theta = 0.25$, respectively.

Another noteworthy observation is the minimal (less than $5\%$) difference in the adherence needed to lower the reproduction number to less than $1$, when the rate of starting PrEP $\theta$ doubles. Specifically, in the casual-only case (Figure 5a), when PrEP uptake rate is $60\%$, then $82\%$ compliance is needed, and nearly the same level ($85\%$) is sufficient when only $30\%$ of susceptible individuals start the treatment. Similarly, when only long-term partnerships are present in the population (Figure 5b), then the minimal threshold adherence would be $98\%$ with $\theta$ being $0.6$. This, once again, suggests that increasing the level of compliance among those already using PrEP could possibly be a better strategy than recruiting more patients into treatment.

4.   Conclusions

In this paper, we used the deterministic $PSI$ model with casual sexual encounters and long-term partnerships to study the effects of pre-exposure prophylaxis (PrEP) on HIV transmission dynamics among MSM. We assumed that PrEP does not provide full protection but lowers the probability of becoming infected by a factor of $(1-qr)$, with $q$ and $r$ denoting treatment adherence and effectiveness, respectively. We derived the rates of infection, calculated the reproduction numbers, and proved global stability of disease-free and endemic equilibria in three different cases, based on the partnerships considered. We also addressed the uniqueness of the endemic equilibrium in each case.

Time series plots (Figure 2) provide a good overview of the differences in the disease progression among the three different cases, showing that the time to equilibration varies from 100 to 400 years. The endemic fraction of infected individuals also ranges from $42\%$, in casual-only case, to $81\%$ when both casual and long-term partnerships are taken into account.

We recognize that the presented results come with certain limitations. In our previous work ^[19] we acknowledged the differences in the levels of infectivity among those in the acute and chronic stages of infection, but in this paper we instead focused on the effects of PrEP and hence included only one infected group. In addition, when considering long-term partnerships, we only considered those with already infected individuals, leaving the case of non-monogamous long-term partnerships with initially susceptible individuals for future work. Introduction of the exclusivity parameter will allow us to study all possible partnership formation scenarios in the model but will add significant level of difficulty when calculating the corresponding rate of infection and then performing full analysis of the disease transmission.

Simpson and Gumel ^[15] indicated the possibility of backward bifurcation when PrEP is introduced to their model, even with no disease mortality. Using the techniques of Martcheva ^[27], we derived the conditions needed to investigate the existence of backward bifurcation when $R < 1$ in our model. Our continuum of the rate of PrEP adherence, rather than two distinct levels used by Simpson and Gumel ^[15], allowed us to go one step further and carefully show that the bifurcations conditions could not be satisfied within the feasible ranges of parameter values. We were able to conclude the lack of backward bifurcation in all three cases, which was also supported with the proofs of global stability of equilibria.

The rate at which susceptible individuals start using PrEP is an important aspect of the fight against the HIV, hence increasing the PrEP coverage may seem like logical intervention. However, the most common concerns among the health professionals and policy makers are the high cost of the treatment per individual and the lowered effectiveness of PrEP when daily medication regime is not strictly followed. With that in mind, proper estimates of PrEP uptake and adherence are very important. Unfortunately, the values of parameters related to PrEP use vary widely in the literature. Punyacharoensin et al. ^[11] used $0.0252$ and $2.7 \times 10^{-7}$ as the respective rates of initiating and terminating the PrEP treatment in the UK. Simpson and Gumel ^[15] assumed $0.01$ overall rate of administration and $0.005$ ($0.0001$) rate of cessation of PrEP by low-adherent (high-adherent) users in Minnesota, USA. On the other hand, in the number of different studies across USA, the PrEP discontinuation rate was observed to be $38\%$ (Hojilla et al. ^[31]) and $40\%$ (Chan et al. ^[32]). The estimates of the PrEP adherence rate in the literature also vary, with researchers assuming it to range from $20\%$ to $100\%$ ^[14,15,33], and possibly including over-reporting ^[34]. We assumed the parameter values listed in Table 1 and used our model to look closely at the effects of varying the uptake rate $\theta$ and the degree of compliance $q$ on the disease dynamics.

Our sensitivity analysis (Figure 3) shows very high impact of adherence to daily PrEP regime on the reproduction number. With the base values of $\theta = 0.1$ and $q = 0.7$, we observe that increasing $q$ by $10 \%$ decreases $R$ by $8-10 \%$, depending on the types of partnerships considered. On the other hand, increasing $\theta$ by $10 \%$ decreases $R$ less than $3 \%$. Related to that are the conclusions we made based on Figures 5 and 6 when looking for the values of parameters that would help eliminate the disease. We noticed a very small difference in the PrEP adherence needed among the users, even when the uptake rate is doubled. Our results are consistent with the work of Jenness et al. ^[14], who used agent-based model simulations to suggest that lower PrEP coverage with optimal adherence is more effective than increased coverage with poor overall adherence.

Finally, the role of long-term partnerships in the spread of incurable diseases is an important consideration in the study of disease dynamics. We showed that the disease dynamics differed depending on the types of partnerships considered in the model. Conditions that imply stability of the disease-free equilibrium are more difficult to achieve, given realistic parameter values, when long-term partnerships are considered. Previous work by Gurski et al. ^[19] compared the long-term partnership model described here to traditional partnership models that explicitly track partnerships for both HIV and HSV-2, both incurable diseases effected by long-term partnerships. The techniques presented in this paper are applicable to a wide range of incurable diseases affected by long-term partnerships.

Acknowledgments

KG was supported by the National Science Foundation (NSF) under Grant No. DMS-1814659. All authors were supported by the National Science Foundation (NSF) under Grant No. DMS-2000044.

Conflict of interest

The authors declare there is no conflict of interest.