Global stability of a pseudorabies virus model with vertical transmission

1.   Introduction

Pseudorabies virus (PRV) infection, also known as Aujeszky's disease (AD), which is caused by pseudorabies virus (PRV) or suid herpesvirus 1 (SuHV-1), can be found all over the world and is common in pigs, cattle, sheep and cats, and is a major economic threat to swine producers^[1,2,3]. It is an infection and all animals, including pigs, have frequent fevers with typical symptoms such as itching and encephalomyelitis. In particular, pigs are natural hosts and reservoirs of the pseudorabies virus. If a dog or cat contacts with the feed form of an infectious pig, Aujeszky's disease may spread. Cattle and sheep may also be infected if they are in contact with sick pigs, resulting in clinical symptoms and possible death ^[4]. The infection can also be age-dependent. Once pigs are infected with pseudorabies, the clinical symptoms vary in different age groups. For example, it will make pregnant sows appear some symptoms such as miscarriage, stillbirth, mummified fetus and infertility, whereas adult sows and boars often present with reproductive and respiratory symptoms. For the piglets within 15 days of age, the mortality rate can reach 100%, and the incidence of weaned piglets can reach 40%, and the mortality rate is about 20% ^[5]. Moreover, PRV can cause adult fat pigs growth stagnation and slow weight gain, and the virus is mainly transmitted through direct or indirect contact. Infected sows can pass to piglets through breast milk.

Pseudorabies virus (PRV) infection is extremely infectious, causing economic losses worldwide in the pig industry. It was first reported in Hungary by Aladar Aujeszky in 1902 ^[6]. Hanson ^[7] referred to the description of the disease in the U.S. in 1813 but it was not known as Aujeszky's disease until 1931. In the mid-20th century, PRV infection was more prevalent in Eastern Europe countries and the Balkans. Since the 1990s, Pseudorabies virus (PRV) infection had been controlled by PR vaccine ^[8] to a certain extent. However, a PR outbreak occurred in northern and eastern China in late 2011 ^[9]. Each outbreak of PR results in severe economic losses and has a considerable impact in the world. Therefore, Pseudorabies virus (PRV) infection has brought many researchers' attentions to study it. For example, the work in ^[1] studied the transmission characteristics of pseudorabies and the infection situation in different periods, and phylogenetic analysis was carried out in ^[8,10,11]. Among those existing results, there were few related mathematical models formulated to study the dynamics of the disease. Recently, PRV becomes more serious concerns for the health of pigs and particularly in the actual pig breeding process in China ^[12]. Pseudorabies virus is listed in an official document of the Chinese government, as a priority infectious disease that needs to be controlled and eradicated in swine breeding farms by the end of 2020 ^[13].The control and prevention of the disease thus is more urgent, and further mathematical modeling study becomes important.

Motivated by the observations above, we formulate in this paper a compartmental susceptible-exposed-infectious-treated (SEIT) model with vertical transmission according to the characters of PRV infection, and study the transmission dynamics of the disease. We first give model descriptions in Section 2. We define the basic reproduction number and investigate the dynamical behavior of the disease free equilibrium in Section 3. We study the existence and uniqueness of a disease-endemic equilibrium in Section 4. Using the Lyapunov functional method ^[14] together with the competitive system theory, we determine the global asymptotic stability of the disease-endemic equilibrium. Finally, we give brief concluding remarks to complete this paper in Section 5.

2.   Model formulation

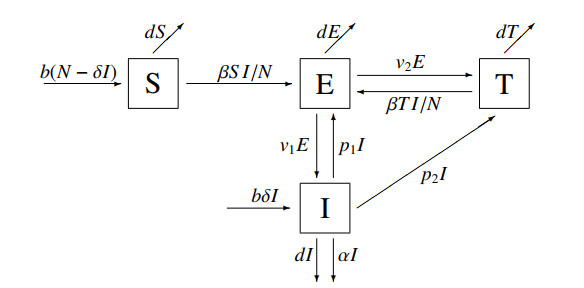
We divide the swine population into four classes, the susceptible (S), exposed (E), infectious (I) and treated (T), such that the total population size is N = S+E+I+T. When the Pseudorabies virus infection is identified, all swines with no symptoms are tested. Those tested positive carry viruses and are from the exposed class E. They are then treated. The usual treatment is injecting high immune serum antibody against pseudorabies. But it only has certain effect on suckling piglets, for adult pigs, the effect of medical treatment is not obvious, but the symptoms are temporarily relieved. An individual who after treatment can go back to the E class after contacting with infected pigs ^[15]. Thus, after the treatment, some of them in class E become infective, progressing to class I with rate $v_1$, because the treatment fails to work, and some of them in class E become partially immune, entering class T with rate $v_2$. The symptomatic infected swines in class I are also treated. After the treatment, they become asymptomatic. Some of them still carry viruses but with no immunity and thus reenter class E with fraction $p_1$, and some of them carry viruses but with partial immunity and thus enter class T with fraction $p_2$. Note that the individuals in class T has only partial immunity and thus become infected after contacting infected swines in class I.

Let the birth rate and natural death rate of the population be $b$ and $d$, respectively. Considering vertical transmission, we assume that a fraction $\delta$ of the offspring produced by infectious swines are infectious. We assume that the offspring from other swines are susceptible. Then the total infectious offspring are $b\delta I$ and the susceptible offspring are $b(N-I) + b(1-\delta)I = b(N-\delta I)$. The horizontal transmission is assumed to take the form of direct contact between the infectious swines and the susceptible or treated swines and the incidence rate $\frac{\beta SI}{N}$ or $\frac{\beta TI}{N}$ thus is of the standard mass-action form. Let $\alpha$ represent the disease-related death rate. The model dynamics are illustrated in Figure 1.

The model dynamics are described by the following differential equations together with non-negative initial conditions:

To make the system biologically meaningful, all parameters are supposed to be positive and less than 1.

Adding all four equations of system (2.1) together leads to

Let

denote the fractions of the compartments $S$, $E$, $I$, and $T$ in the population, respectively. It follows from (2.2) that

and then system (2.1) becomes

Since $x+y+z+w = 1$, the dynamics of system (2.3) are equivalently described by

Define a closed set

Then $\Omega$ is a positive invariant set with respect to system (2.4) ^[16]. We thus focus our investigation on the dynamical features of system (2.4) on $\Omega$.

3.   Dynamics of disease free equilibrium $P_0$

It is easy to see that system (2.4) always has a disease-free equilibrium, $P_0 = (1, 0, 0)$. According to ^{[17,18,19,20]}, the basic reproduction number of system (2.4) is

.

We have the following results.

Theorem 1. Consider system (2.4). If $\Re_0 < 1$, then the disease-free equilibrium (DFE) $P_0 = (1, 0, 0)$ is the unique equilibrium, which is globally asymptotically stable on $\Omega$ (i.e., the disease dies out regardless of its initial values) and if $\Re_0 > 1$, then the DFE $P_0$ is unstable.

Proof

The Jacobian matrix of system (2.4) at $P_0$ is

It follows from

where $m = p_1+p_2+b+\alpha-b\delta > 0$, $n = v_1+v_2+b > 0$ and $m+n > 0$, that the eigenvalues of $J(P_0)$ satisfy

Suppose $\Re_0 < 1$. Then $mn-v_1p_1-v_1\beta > 0$, and (3.2) ensures that all eigenvalues $\lambda_i$, $i = 1, 2, 3$, are negative. Consequently, $P_0$ is locally stable in $\Omega$.

If $\Re_0 > 1$, then $mn-v_1p_1-v_1\beta < 0$, and it follows from (3.2) that $\lambda_2$ and $\lambda_3$ are of opposite sign; that is, either $\lambda_2 > 0$, $\lambda_3 < 0$ or $\lambda_2 < 0$, $\lambda_3 > 0$. As a result, the DFE $P_0$ is unstable if $\Re_0 > 1$.

To show that the DFE is globally attractive for $\Re_0 < 1$, we consider a Lyapunov functional defined by

Then $V$ is positive and the derivative of $V$ along the solutions of system (2.4) is given by

Using the method of calculating the maximum value of multivariate function, we get that in region $\Omega$,

and then

Since $\Re_0 < 1$, $v_1\beta < mn-v_1p_1$ and thus

Recall $n = v_1+v_2+b$. Then we have $mn-v_1p_1 > \max\{v_1\beta, v_1\alpha, \alpha n\}$ when $\Re_0 < 1$. Therefore,

In addition, $\frac{dV}{dt} = 0$ if and only if $y = 0$ and $z = 0$. Moreover, $\Omega = \{P_0\}$ is the largest invariant set in $\{(x, y, z)\in\Omega|\frac{dV}{dt} = 0\}$. According to LaSalle's Invariance Principle (^[21], Chapter 2, Theorem 6.4), the DFE $P_0$ is globally asymptotically stable on $\Omega$ under the condition $\Re_0 < 1$.

4.   Dynamics of the disease-endemic equilibrium $P^{*}$

In this section, we study the existence and stability of the disease-endemic equilibrium $P^{*} = (x^{*}, y^{*}, z^{*})$ with $x^{*} > 0$, $y^{*} > 0$ and $z^{*} > 0$. Let $a_1 = \alpha(\beta-\alpha)$, $a_2 = (\alpha-\beta)m+\alpha n-v_1\beta$ and $a_3 = v_1\beta+v_1p_1-mn$. We have the following results.

Theorem 2. Suppose $\Re_0 > 1$. Then system (2.4) admits a unique disease-endemic equilibrium $P^* = (x^{*}, y^{*}, z^{*})$, where

The disease-endemic equilibrium $P^*$ is locally asymptotically stable.

Proof

The components of the disease-endemic equilibrium must satisfy the following system

Obviously, (4.1) has no solutions in the form of $(x_1, y_1, 0)$ or $(x_2, 0, z_2)$ with $x_1 > 0$, $y_1 > 0$ or $x_2 > 0$, $z_2 > 0$. In the following, we look for the solution $(x^{*}, y^{*}, z^{*})$ of (4.1) with $x^{*} > 0$, $y^{*} > 0$ and $z^{*} > 0$. It is straightforward to find that

From (4.3) and (4.4), we have

Thus

Recall $a_1 = \alpha(\beta-\alpha)$, $a_2 = (\alpha-\beta)m+\alpha n-v_1\beta$ and $a_3 = v_1\beta+v_1p_1-mn$. Then (4.6) can be rewritten as

Notice that $m = p_1+p_2+b+\alpha-b\delta > 0$ and $n = v_1+v_2+b > 0$. Then, for $\Re_0 > 1$, we have

and thus $\beta > \alpha$. Further, it follows from

that the associated discriminant of the quadratic equation $f(z^{*}) = 0$ is

Moreover, from (4.7) and (4.9), we have

and

Therefore, there is at least one positive $z^{*}$ satisfying $0 < z^{*} < 1$.

We next show the uniqueness of $z^{*}$ in the interval $(0, 1)$ in the following two cases.

$\bf (I)$ If $\Delta = 0$, direct computation yields that $z^{*} = -\frac{a_2}{2a_1} > 0$ is the unique solution of the quadratic equation (4.7).

$\bf (II)$ if $\Delta > 0$, we suppose $f(z^{*}) = 0$ admits two unequal roots $z^{*}_1$ and $z^{*}_2$. Without loss of generality, let $z^{*}_1 < z^{*}_2$. Then

If $0 < z^{*}_{1} < 1 < z^{*}_{2}$, then obviously, $z^{*}_{1}$ is the unique solution of equation (4.7) in the interval $(0, 1)$.

If $0 < z^{*}_1 < z^{*}_2 < 1$, since $a_1 > 0$ and the expression of $f(z^{*})$ in (4.7), we get both $f(0) > 0$ and $f(1) > 0$, which contradicts $f(0)\cdot f(1) < 0$. Hence, equation (4.7) possesses only one root, say $z^{*}_1$.

Based on (4.2), (4.3), and the analysis above, it follows that if $\Re_0 > 1$, system (2.4) admits a unique disease-endemic equilibrium $P^* = (x^{*}, y^{*}, z^{*})$, where

We now investigate the local stability of $P^{*}$ as follows.

Linearizing (2.4) around $P^{*} = (x^{*}, y^{*}, z^{*})$, we obtain the characteristic equation given by

where $m_1 = n+(\beta-\alpha)z^{*}$, $m_2 = -\beta-p_1+(\beta-\alpha)y^{*}+2\beta z^{*}$, $m_3 = m-2\alpha z^{*}$,

Recall that (4.8) implies $\beta > \alpha$. Then from (4.11), we have $\eta_1 = -(\beta-\alpha)z^{*}-b < 0$ and $\eta_2$ and $\eta_3$ satisfying the equation

Write $\Delta = a_2^{2}-4a_1a_3$. Then it follows from (4.9) and

that

and together with $\Re_0 > 1$

On the other hand, it follows from $y^{*} = \frac{m-\alpha z^{*}}{v_1}z^{*}$ that

Substituting ${z^{*}} = \frac{-a_2-\sqrt{\Delta}}{2a_1}$ into (4.15), we then have

since $\Delta = a_2^{2}-4a_1a_3 < a_2^{2}$ and $a_2 < 0$ which yields $-\sqrt{\Delta} > a_2$.

Hence, both $\eta_2$ and $\eta_3$ have negative real parts and thus we complete the proof of Theorem 2.

In addition to Theorem 2, we state our main result of the present section below.

Theorem 3. When $\Re_0 > 1$, if $p_{1}\geq\max\{\beta, b\}$, then the disease-endemic equilibrium $P^{*}$ of System (2.4) is globally asymptotically stable.

Inspired by ^[22,23], we use the theory of competitive systems of differential equations to prove global stability of the endemic equilibrium $P^{*}$ of system (2.4). We first state the definition of competitive systems as follows.

Let $h(x)$ be continuously differentiable and $\frac{\partial h(x)}{\partial x}$ be the Jacobian matrix of $h(x)$. If there is a diagonal matrix $H = \text{diag}(\epsilon_1, \epsilon_2, \ldots, \epsilon_n)$, where each $\epsilon_i$ is either 1 or -1 $(i = 1, 2, \ldots, n)$, such that the non-diagonal elements of $H\frac{\partial h(x)}{\partial x}H$ are non-positive for all $x\in\Omega$, then the differential equations $\frac{dx}{dt} = h(x)$ are called competitive systems ^{[21,22,24,25]}.

For system (2.4), the associated Jacobian matrix $J(x, y, z)$ is given by

Take matrix $H$ as $H = diag(-1, 1, - 1)$. Then

Let $p_{1}\geq\beta$. Then

and

By (4.17), (4.18) and $-v_1 < 0$, it is easy to obtain that the non-diagonal elements of $HJ(x, y, z)H$ are all non-positive in $\Omega$. Hence System (2.4) is a competitive system in region $\Omega$. It is known that 3-dimensional competitive systems have the Poincaré-Bendixson property ^[25,26]. Similar to ^[21,22], we have:

Lemma 4.1. Consider system (2.4). An arbitrary nonempty compact $\omega$-limit set of system (2.4), in the interior of $\Omega$, can only be a periodic solution or the endemic equilibrium $P^{*}$.

To get the global stability of the endemic equilibrium $P^*$, we state a criterion for the asymptotic stability of a non-constant periodic solution to System (2.4) as follows.

Lemma 4.2. Suppose that $\gamma = \{p(t):0\leq t\leq \omega\}$ is a non-constant periodic solution of system (2.4). If $\Re_0 > 1$, $p_{1}\geq\max\{\beta, b\}$, then $p(t)$ is asymptotically stable.

Proof

Suppose $p(t)$ is a non-constant periodic solution of system (2.4). Let $\frac{dy(t)}{dt} = \frac{\partial h(p(t))}{\partial x}y(t)$ be the linearized system of system (2.4) at $p(t)$. According to Muldowney ^[27], when the zero solution of the second compound equation $\frac{dz(t)}{dt} = \frac{\partial h(p(t))^{[2]}}{\partial x}z(t)$ is asymptotically stable, the zero solution of $\frac{dy(t)}{dt} = \frac{\partial h(p(t))}{\partial x}y(t)$ is also asymptotically stable. Therefore, in order to get the asymptotical stability of $p(t)$, we show that the zero solution of $\frac{dz(t)}{dt} = \frac{\partial h(p(t))^{[2]}}{\partial x}z(t)$ is asymptotically stable.

Write $p(t) = (\tilde{x}(t), \tilde{y}(t), \tilde{z}(t))$ and let $X = x-\tilde{x}(t)$, $Y = y-\tilde{y}(t)$ and $Z = z-\tilde{z}(t)$, then the linearized System (2.4) at $p(t)$ is

Thus the second compound matrix $J^{[2]}(x, y, z)$ of $J(x, y, z)$ is

where

Therefore, the corresponding $\frac{dz(t)}{dt} = \frac{\partial h(p(t))^{[2]}}{\partial x}z(t)$ can be expressed by

In order to show the asymptotic stability of system (4.20) around the solution zero, consider the following functional:

Then $V(X, Y, Z; \tilde{x}(t), \tilde{y}(t), \tilde{z}(t))\geq0$ for $\tilde{x}(t)$, $\tilde{y}(t)$ and $\tilde{z}(t))$ all positive periodic functions. Moreover, $V(X, Y, Z; \tilde{x}(t), \tilde{y}(t), \tilde{z}(t)) = 0$ only if $X = Y = Z = 0$. Since $V(X, Y, Z; \tilde{x}(t), \tilde{y}(t), \tilde{z}(t))$ is not continuously differentiable, similar to ^{[21,24,28,29]} or ^[30], we consider the right-upper derivative of $V(X, Y, Z; \tilde{x}(t), \tilde{y}(t), \tilde{z}(t))$ along the solution curve of System (4.20). Let $D_{+}$ denote the right-upper derivative. Since $p_{1}\geq\max\{\beta, b\}$, $\beta > \alpha$ and $0 < \tilde{x}(t) < 1$, $(\beta-\alpha)\tilde{x}(t)+b\delta < \beta\tilde{x}(t)+p_{1} < \beta+p_{1}$. Direct calculation then yields

And

In virtue of (4.22) and (4.23), we get

where

Notice that $(\tilde{x}(t), \tilde{y}(t), \tilde{z}(t))$ is the positive solution of system (2.4). Then

$\Re_0 > 1$, $p_{1}\geq\beta > \alpha$ and $0 < \tilde{z}(t) < 1$, which deduces $p_{1}-\alpha\tilde{z}(t) > 0$, and substituting (4.26) into (4.25) yields

Meanwhile, since $\tilde{w}(t) = 1-\tilde{x}(t)-\tilde{y}(t)-\tilde{z}(t)$,

Hence,

and

In view of above analysis, we have

and

which indicates that the zero solution of system (4.20) is asymptotically stable. Therefore, the non-constant periodic solution $p(t)$ of system (2.4) is asymptotically stable.

In order to present the proof of Theorem 3 by the result given in ^[31], we need the following results:

Lemma 4.3. The DFE $P_0$ of system (2.4) is the unique $\omega$-limit point of system (2.4) on the boundary of $\Omega$. If $\Re_0 > 1$, $P_0$ cannot be the $\omega$-limit point of any orbit starting in the interior of $\Omega$.

Proof When $\Re_0 < 1$, the DFE $P_0$ is the unique disease-free equilibrium of system (2.4). We say that for any $t_0\ge 0$, the trajectory $\varphi(P, t)$ ($t_0\leq t < +\infty$) is the positive half orbit of system (2.4). From Theorem 1, we know that $P_0$ is also a singular point on boundary $\Omega$ and $\Omega = \{P_0\}$. Thus, the DFE $P_0$ is the unique $\omega$-limit point of System (2.4) on the boundary of $\Omega$. When $\Re_0 > 1$, besides the disease-free equilibrium $P_0$, there is a unique disease-endemic equilibrium $P^{*}$. Since $P_0$ is unstable when $\Re_0 > 1$, $P_0$ can not be the $\omega$-limit point of any orbit starting in the interior of $\Omega$. The proof is complete.

With the aid of Lemmas 4.3, 4.4 and 4.5, we are in the position to complete the proof of Theorem 3.

Proof of Theorem 4.2

When $\Re_0 > 1$, system (2.4) admits a unique disease-endemic equilibrium $P^{*}$. The asymptotic stability of the disease-endemic equilibrium $P^{*}$ has been proved previously. Now we show that the attraction domain of $P^{*}$ is the interior of $\Omega$.

Let $U$ be the domain of attraction of $P^{*}$ in $\Omega$. From the asymptotic stability of $P^{*}$, $U$ is a nonempty open subset in $\Omega$. Otherwise, suppose $U$ is not the interior of $\Omega$. Then the boundary $\partial U$ of $U$ has a nonempty intersection with the interior of $\Omega$. We denote this intersection by $\Gamma$. Since both $U$ and $\overline{U}$ are positive invariant sets of System (2.4), $\partial U = \overline{U}-U$ and $\Gamma$ are also positive invariant sets of system (2.4). The limit set $\gamma$ of system (4.22) is contained in $\Gamma$. By Lemma 4.3, the limit set of system (2.4) can only be $P^{*}$ or periodic solution $p(t)$. Lemma 4.4 tells us that the periodic solution $p(t)$ of system (2.4) is asymptotically stable. Then $\Gamma$ is bound to attract solutions in its domain, which contradicts that of $\Gamma$ in $\partial U$. Therefore, the disease-endemic equilibrium of System (2.4) is globally asymptotically stable. This completes the proof.

Remark 1. From the result in Theorem 3 and its proof, we obtain that system (2.4) is persistent under the condition of $\Re_0 > 1$ and $p_{1}\geq\max\{\beta, b\}$ ^[32].

5.   Concluding remarks

In this paper, we formulated a susceptible-incubating-infected-treated (SEIT) mathematical model with vertical transmission for the Porcine pseudorabies infection transmission and studied the model dynamics. We defined a threshold, the basic reproduction number, $\Re_0$, and showed that the DFE $P_0$ is globally asymptotically stable and the disease will die out, regardless its initial sizes, if $\Re_0 < 1$. The DFE $P_0$ is unstable and invasion is always possible if $\Re_0 > 1$ ^[18,33]. We also showed that there is only one positive equilibrium $P^*$ in $\Omega$, which is globally asymptotically stable and the disease is persistent under the conditions $\Re_0 > 1$ and $p_{1}\geq\max\{\beta, b\}$. Furthermore, the basic reproduction number $\Re_0$ is strictly increasing with respect to the contact rate $\beta$. Therefore, isolation of infected pigs and appropriate feeding densities will facilitate the prevention and control of outbreaks of pseudorabies in pigs.

Acknowledgements

The authors gratefully acknowledge Prof. Jia Li of University of Alabama in Huntsville for his constructive suggestions and useful corrections. The authors also wish to thank the handling editor and the anonymous referees for their valuable comments and suggestions.

Conflict of interest

The authors declare no conflicts of interest in this paper.