How fast is the linear chain trick? A rigorous analysis in the context of behavioral epidemiology

1.   Introduction

It is widely known that delay equations originate dynamical systems of infinite dimension ^[1]. Their treatment in view of stability and bifurcation analyses thus poses several challenges. Then it is not a surprise that the issue still attracts the attention of many researchers after several decades of efforts. A major direction to attack the problem is undoubtedly represented by the reduction to finite dimension, either exactly or through approximation.

The recent work ^[2] represents an elegant and up-to-date reference for the first option, also useful as a starting point for the relevant branch of literature. In particular, it shows up as a modern account of the possibility of reducing a delay equation to an equivalent finite-dimensional system of Ordinary Differential Equations (ODEs). This has been well known since long for the case of delays modeled according to the Erlang distribution. In particular, the corresponding methodology originated from the pioneering work ^[3] in queueing theory and nowadays, in the context of delays, it undergoes the name of linear chain trick. The term has been probably proposed by MacDonald ^[4,5], even though the technique dates back to the late sixties ^[6,7,8], at least as far as fields like epidemiology, population dynamics and evolutionary systems in general are concerned.

When an exact reduction is not available, the study of relevant approximations through ODEs becomes central. In this sense, Breda, et al.^[9] proposes a general numerical approach to address a broad class of functional problems. Nevertheless, in the early eighties the subject was already alive. Busenberg and Travis ^[10] and Cooke and Grossman ^[11] represent important contributions from those years, with particular reference to biological models, where indeed delays emerge naturally. Therein, the linear chain trick is investigated in view of analyzing the stability of steady states (in the first) or as a way to gain insight into the pros and cons of using discrete or distributed delays in modeling (in the second).

Essentially, and on the one hand, the linear chain trick is a smart way to construct a system of ODEs equivalent to a problem with a delay modeled according to the Erlang distribution^*. The number of ODEs corresponds to the (integer) shape parameter of the latter. As this number grows, the variance of the distribution decreases and the delay values tend to concentrate around their mean value. If we let this number grow unbounded, in the limit we obtain the Dirac's delta distribution, corresponding to a problem with a single discrete delay. Thus, on the other hand, the linear chain trick can be interpreted as a mean to approach a fixed delay through a sequence of distributed delays. Under this point of view, it is natural to ask how the relevant stability properties behave, a question already central in ^[10,11], but still contemporary, see, e.g., ^[12] or ^[13] concerning the computation of the basic reproduction number.

^*Note that the linear chain trick works as the Erlang distribution is in fact a sum of independent exponential distributions.

Eventually, despite the evident interest that the literature devoted to the argument, there has been no rigorous study on the rate at which the linear chain trick makes the sequence of distributed delays converge to the limit of concentrated delay, together with the associated stability features. It is anyway worth recalling from page 169 in ^[5] that a general degree should be kept in mind when one applies the linear chain trick, this degree being indeed the number of ODEs used to "decompose" the delay. Let us point out that some effort in this direction is reported in ^[14,15] on investigating experimentally the effect of increasing the degree of approximation. As a general outcome, it is observed that on the way towards a fixed delay the chances of instability grow, mainly due to sustained oscillations.

In the works just mentioned the delay represents the infectious period of childhood viral diseases. The author addresses the study of more realistic distributions of the latter (viz. Erlang with larger shape parameter) by using the linear chain trick, therein named method of stages after the original work ^[3]. The biological field of infectious diseases and epidemics is a major area of investigation. Recently it gained even more attention, also outside the scientific community, due to the impact of vaccination strategies in modern societies as opposed to the emerging of often clamoring campaigns of vaccine hesitancy. It is not surprising then that the discipline of behavioral epidemiology arose lively, with the broad target of studying the effect of the "individual behavior as a key determinant of infection trajectories" ^[16]. Besides the two cornerstones ^[17,18] and many other contributions (see, e.g., ^{[19,20,21,22,23,24,25,26]}), d'Onofrio, et al. ^[27] is a thorough representative of this new branch of mathematical biology. In it, the authors study the effect of the so called rational exemption, the phenomenon by which parents relate the decision to whether vaccinate or not their children to the current as well as past information available on the disease. They propose to model the information variable through the Erlang distribution, even though in the end only the degenerate exponential case of fading memory is elaborated. The main focus is on the stability of the endemic equilibrium and the appearance of stable oscillations through Hopf bifurcations is demonstrated. We mention also ^[28], which is seemingly the first work in the field about distributed delays, and ^[29] on Hopf bifurcations in structured populations.

In view of the above and taking inspiration from ^[27], the current work chases two objectives.

On the one side, we aim at extending the analysis of stability of the endemic equilibrium of the SIR model studied in ^[27], investigating both the general Erlang case with varying shape parameter, as well as the limiting case of concentrated memory. The latter alone already represents a novel contribution in that the relevant analysis makes use of modern numerical methods for the stability analysis of delay systems, e.g., ^[30,31,32]. As such, it is our hope that this first attempt will open the door to further extensions towards more realistic models including even different (type and number of) delays.

On the other side, as the linear chain trick is used to deal with the general Erlang distribution, we perform a rigorous study of how the latter approaches the concentrated case by increasing its shape parameter. In particular, we analyze the behavior of the rightmost eigenvalues of the relevant variational problems, eventually proving that those of the Erlang case converge to those of the concentrated case at a linear rate in terms of the number of ODEs used to reduce the distributed delay. To the best of our knowledge, this question has never been addressed in the literature.

In addition to the contributions described above, our results confirm that when the delay distribution presents a lower variance, systems are more prone to instability. This instability shows up as a series of stability switches through couples of destabilizing/stabilizing Hopf bifurcations. In particular, as a clear outcome, we obtain that the number of these switches increases from a single one in the case of exponential distribution to possibly infinitely-many in the case of concentrated memory. We also give a rigorous argument justifying the latter result based on ^[33].

Finally, we show that the proof of linear convergence mentioned above can be extended to models described by a general system of ODEs in which there is a dependence on an "information" variable modeled through a distributed delay. Therefore, the applicability of the proposed analysis goes far beyond the SIR model used here as a prototype.

In the sequel we present in section 2 the SIR model just mentioned, analyzing the case of fading memory in section 2.1, the case of concentrated memory in section 2.2 and the general Erlang distribution in section 2.3. In section 2.4 we collect the outcome of the experimental analysis in terms of stability charts. The convergence of the linear chain trick in terms of eigenvalues is proved in section 3 for the prototype SIR model, and then it is extended in section 4. Some concluding remarks close the work in section 5.

2.   Prototype model and kernels

Following ^[27], let us consider the SIR model for a non-fatal pediatric disease in a constant homogeneously mixing population with vaccination at birth

where $\mu$ represents both the constant fertility and mortality rates, $\beta$ the constant contact rate, $\nu$ the constant recovery rate and $p:[0, +\infty)\rightarrow\mathbb{R}$ the vaccination coverage function. The latter gives the fraction of vaccinated newborns, which depends on the information about the disease available to their parents. This information is described by the map $M:[0, +\infty)\rightarrow\mathbb{R}$ given by

which considers the past values of the disease prevalence $g:[0, +\infty)\times[0, +\infty)\rightarrow\mathbb{R}$ as weighted through a memory kernel $K:[0, +\infty)\rightarrow\mathbb{R}$, non-negative and normalized as

The coverage function $p$ is assumed to be piecewise smooth and non-decreasing in $M$, so that the decision to vaccinate is directly correlated to the disease prevalence. The latter is a smooth function of both susceptible and infected individuals, assumed to be increasing in the second. Moreover, $g(S, 0) = 0$ independently of the values of $S$: In absence of infection there is indeed no information. Note that $S$, $I$, $R$ and $V$ represent fractions with respect to the total (constant) population.

The equations for $R$ and $V$ are linear inhomogeneous ODEs, so that their solution is straightforward through the variation of constants formula once $I$ and $M$ are given. Therefore, in view of investigating the relevant dynamics, it is enough to consider the reduced model

where we directly add (2.1) to the equations for $S$ and $I$.

It is not difficult to see that system (2.3) presents a unique endemic equilibrium $(\overline S, \overline I, \overline M)$ with $\overline S = (\mu+\nu)/\beta$, $\overline I$ the solution of

and $\overline M = g(\overline S, \overline I)$. Note that $\overline I$ is unique since in Eq (2.4) the left-hand side is decreasing in $I$ while the right-hand side is increasing. Moreover, and more important, the equilibrium is independent of the choice of the memory kernel $K$, at least as long as Eq (2.2) holds. The same cannot be said for its local asymptotic stability and, indeed, the focus of this work is at investigating how the choice of the memory kernel influences the latter.

To this aim, we first analyze two prototype choices, i.e., the case of fading memory

where $a > 0$ plays the role of decaying rate, and the case of concentrated memory

where $\delta$ is the Dirac's delta at $\tau > 0$. We call delay the latter, observing that it represents a fixed time instant in the past where all the information about the disease is assumed to be concentrated.

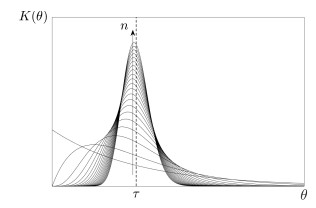
The two cases above can be seen as the extrema of a spectrum of choices, in which the information is distributed on $[0, +\infty)$ around a mean value with a certain variance. In this rispect, we take into consideration also the kernel

where

is the Erlang distribution, i.e., a Gamma distribution with integer shape parameter $n\in\mathbb{N}\setminus\{0\}$ and rate parameter $a > 0$. In particular, ${\rm Erl}_{n, a}$ has mean value $n/a$ and variance $n/a^{2}$, so that by fixing

we end up with a mean value $\tau$ and variance $\tau^{2}/n$. As anticipated, by letting $n = 1$ we recover exactly the case of fading memory Eq (2.5), while by letting $n\rightarrow\infty$ we obtain the case of concentrated memory Eq (2.6), see Figure 1.

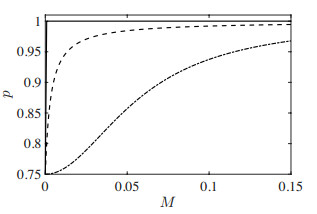
As far as the coverage function is concerned, in the sequel we initially fix

with the specific choice

In (2.10) the constant $p_{0}\in(0, 1)$ represents the fixed fraction of population that vaccinate their children independently of the available information $M$, while the function $p_{1}:[0, +\infty)\rightarrow\mathbb{R}$ portrays the concept of rational exemption (vaccinate less/more with more/less immune individuals) page 304, note 1 in ^[27]. With (2.11) $p$ is piecewise smooth with slope $c > 0$ in the first part and it reaches the saturation value $1-p_{0}$ for larger values of $M$. Other choices are considered in section 2.4.

Similarly, as for the disease prevalence, we perform most of the analysis by choosing

for $k$ some positive constant^†.

^†This choice is motivated by the aim of reproducing the results of ^[27]. Note, however, that the general setting discussed in section 4 includes also the choice $g(S, I) = kSI$, as well as more general ones

In the following sections, keeping the choices above, we investigate the local asymptotic stability of the endemic equilibrium $(\overline S, \overline I, \overline M)$ for varying $\tau$ (and possibly $c$) with either Eq (2.5) in section 2.1, Eq (2.6) in section 2.2 and Eq (2.7) in section 2.3.

Remark 2.1. Condition (2.9) is implicitly assumed in the sequel, even when not explicitly used.

2.1.   Fading memory

Let us consider the choice (2.5) and rewrite the third of system (2.3) as

By differentiating the latter system (2.3) reduces to the system of $3$ ODEs

The local asymptotic stability of the endemic equilibrium $(\overline S, \overline I, \overline M)$ is analyzed in ^[27] by resorting to the Routh-Hurwitz criterion as applied to the matrix associated to the relevant linearization, i.e.,

where $g_{S}$ and $g_{I}$ denote the partial derivatives of $g$ with respect to $S$ and $I$, respectively. Here, instead, we compute the eigenvalues of matrix (2.13) in view of generalizing this approach in the forthcoming sections: A rightmost eigenvalue with negative real part guarantees asymptotic stability, otherwise any eigenvalue in the right-half of $\mathbb{C}$ determines instability.

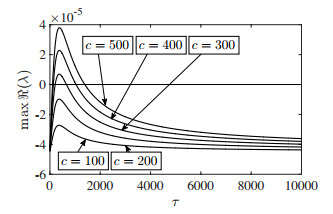
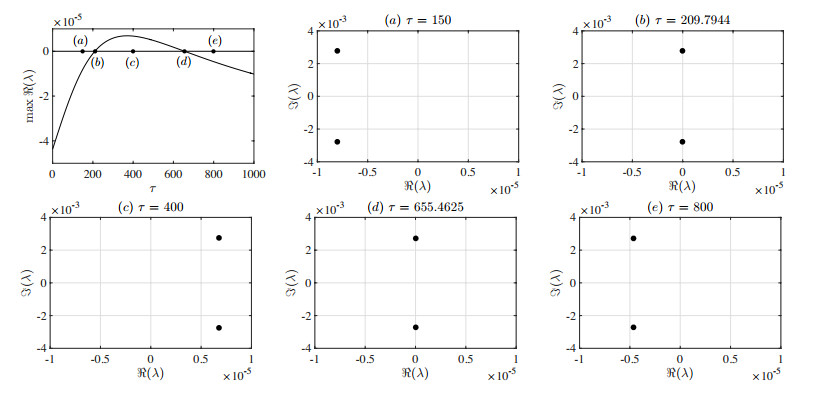
Figure 2 reproduces in this sense the same results of Figure 1 in ^[27] for the choices (2.10), (2.11) and (2.12), and for the values of the concerned parameters as in Table 1 (which depict measles in a low-mortality population ^[27]). Let us highlight that for sufficiently large $c$ at most one instability interval occurs in the domain of $\tau$ (recall Eq (2.9)). This is originated by a couple of Hopf bifurcations, the first destabilizing and the other stabilizing, Figure 3. In the latter, the eigenvalues are computed by standard routines for matrix eigenvalues (specifically, eig in Matlab) and the bifurcation values for the delay $\tau$ are found by standard nonlinear solvers (specifically, fzero in Matlab).

2.2.   Concentrated memory

Let us consider now the choice Eq (2.6), by which model (2.3) reduces to

System (2.14) is made of $2$ ODEs coupled to an algebraic equation with delay. This makes the corresponding dynamical system infinite-dimensional, with state space a set of functions defined on the delay interval $[-\tau, 0]$. For this and the following related issues we refer to ^[34]. Alternatively, one can substitute the third equation for $M$ into the first one, obtaining a more conventional DDE for $S$ coupled to the ODE for $I$, for which we refer to ^[32] as far as the following is concerned. Anyway we feel free to use one formulation or the other depending on the convenience from time to time.

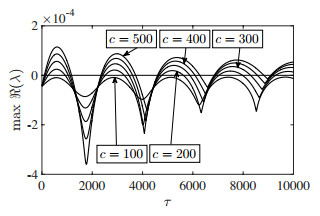
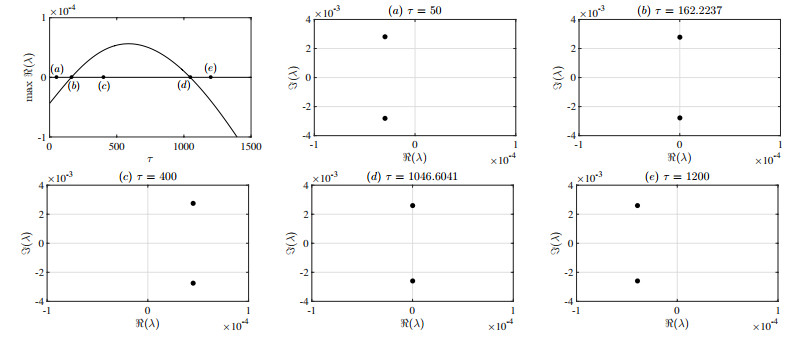
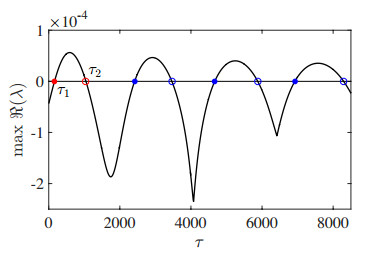
The endemic equilibrium $(\overline S, \overline I, \overline M)$ of system (2.14) remains unchanged, although the analysis of its local asymptotic stability is far less trivial due to the infinite dimension. The principle of linearized stability still holding, the problem reduces to determine the spectrum of suitable linear operators associated to the linearized system. These are either the semigroup of solution operators or its infinitesimal generator. Of course, numerical approximation is needed, as they are operators on Banach spaces of functions. In this regard, we rely on the pseudospectral methods in either ^[35] or ^[32] depending on the chosen formulation, both furnishing accurate approximations of the rightmost eigenvalue, which is the stability determining one. The results are illustrated in Figure 4, which is the analogous of Figure 2 but for Eq (2.6) replacing Eq (2.5). Now infinitely-many intervals of instability can appear, always due to Hopf bifurcations, Figure 5 (the analogous of Figure 3). A rigorous argument behind this claim is given next.

Let us resume from ^[33] the concepts of kernel and offspring sets, introduced therein for linear autonomous systems with delay. Let us stress that this kernel has nothing to deal with the memory kernel: To avoid confusion we use italic fonts when dealing with the former. We anticipate from Eq (3.8) in section 3 that the characteristic equation associated to the linearized version of system (2.14) contains the complex exponential $e^{-\lambda\tau}$, a well-known fact indeed for systems with a discrete delay $\tau$. Nontrivial conjugated roots on the imaginary axis, say $\lambda = \pm\beta{\rm i}$, make the exponential periodic in $\beta\tau$. Given $\beta$, let us define the kernel set

This in turn generates the offspring set

Therefore any value in the kernel set gives rise to a periodic sequence of delay values in the relevant offspring set. Note however that one has to compute only the kernel set, since the offspring set follows automatically. In the specific case (2.14), for any given value of $c$ over a certain threshold, there are just two values of $\beta$ giving rise to Hopf bifurcations, one destabilizing and one stabilizing. Correspondingly we can find the relevant kernel sets, each of which consists of only a single delay value. As a convention, in the sequel we use the index $1$ for the delay value $\tau_{1}$ originating the destabilizing Hopf bifurcation and the index $2$ for the delay value $\tau_{2}$ originating the stabilizing Hopf bifurcation. These two values of $\tau$ correspond to the first two crossings of the horizontal axis in Figure 4. All the other crossings are obtained as offspring sets, and are indeed periodically distributed along the delay axis with period $2\pi/\beta$. Let us observe anyway that the instability intervals created by the two sequences of $\tau$ values may merge or disappear at some points, given that the period $2\pi/\beta$ changes with $\beta$. Eventually, we remark that this theoretical argument is validated experimentally with rather high accuracy, see Table 2 and Figure 6. In Table 2 exact means computed as $\tau+2\pi j/\beta$ once $\beta$ and $\tau$ are computed for the kernel set.

2.3.   Erlang distribution and the linear chain trick

Let us consider now the choice Eq (2.7) and define the auxiliary variables

Clearly $Z_{n}(t) = M(t)$, while differentiation allows to transform system (2.3) into the system of $n+2$ ODEs

This procedure is known as linear chain trick, as already anticipated and discussed in the Introduction.

The endemic equilibrium is now $(\overline S, \overline I, \overline M, \ldots, \overline M)$: It differs just in the presence of the auxiliary components which, being all equal to the information compartment, do not bring any novelty in. By proceeding as in section 2.1, we compute the eigenvalues of the matrix of the linearized system, i.e.,

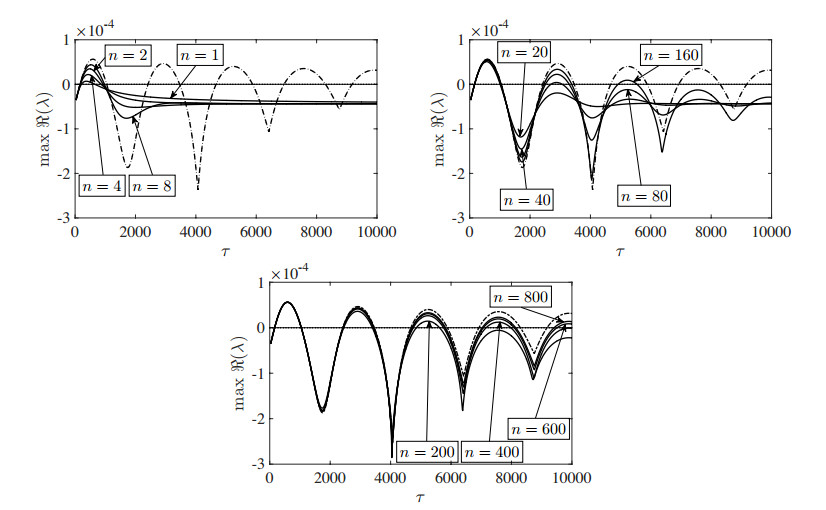
in $\mathbb{R}^{(n+2)\times(n+2)}$. Figure 7 shows the analogous results of Figures 2 and 4. It emerges clear that the curve representing the real part of the rightmost eigenvalue(s) of matrix (2.16) gets close to that relevant to the case of concentrated memory as $n$ increases: Indeed, more and more instability intervals due to Hopf bifurcations appear in the direction of increasing $\tau$ as long as $n$ grows. We omit to include the analogous of Figures 3 and 5 since qualitatively unchanged. We instead show in Figure 8 the values of $\tau$ for varying $n$ corresponding respectively to the first (destabilizing) and the second (stabilizing) Hopf bifurcations. Some of these values are provided in Table 3 for reference.

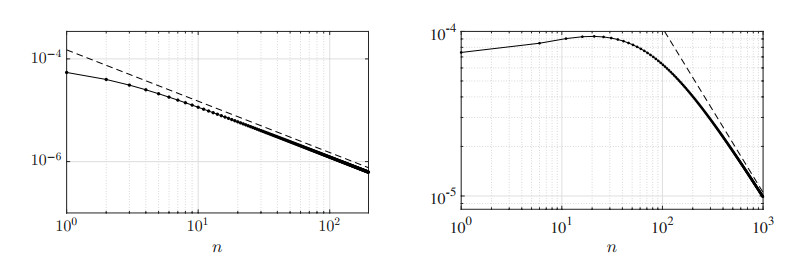
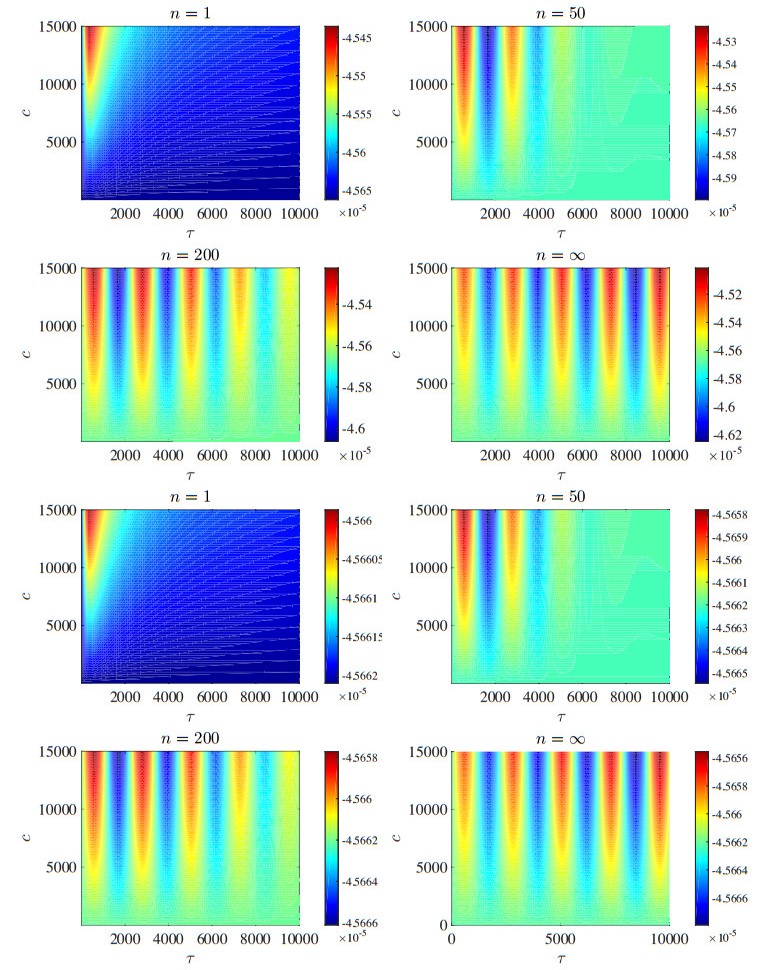
Although we leave a detailed investigation of this behavior to section 3, let us anticipate that, experimentally, we find that the difference between the real part of the rightmost eigenvalue(s) of cases (2.6) and (2.7) for fixed values of $\tau$ is $O(1/n)$, Figure 9. In section 3, as a major contribution of the present work, we rigorously show that this is indeed the case.

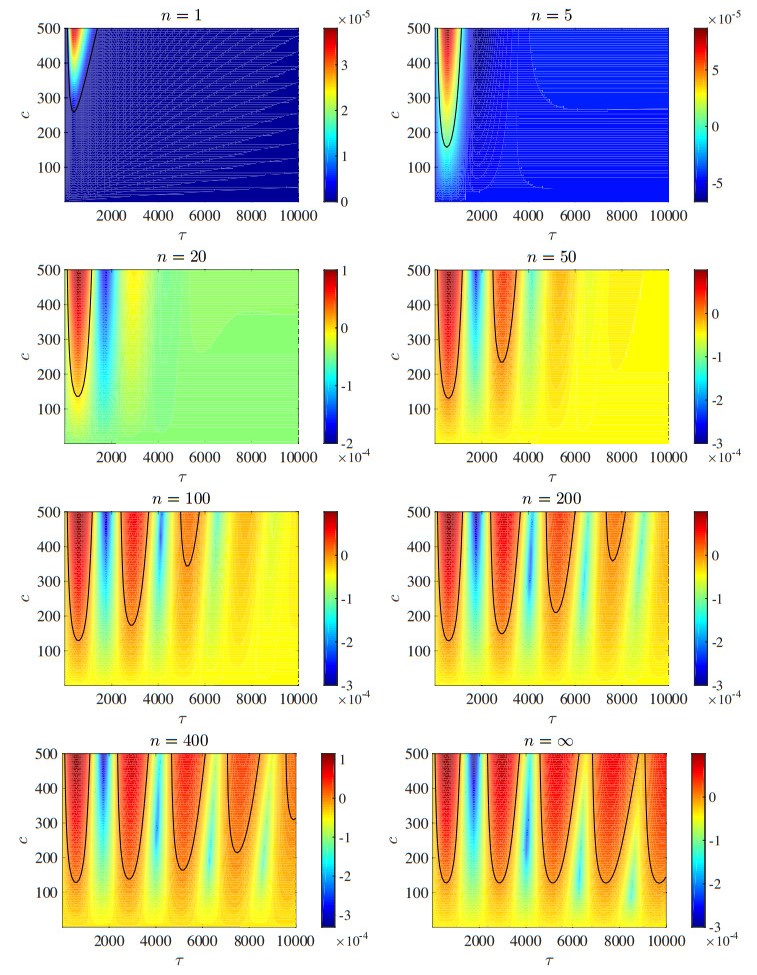
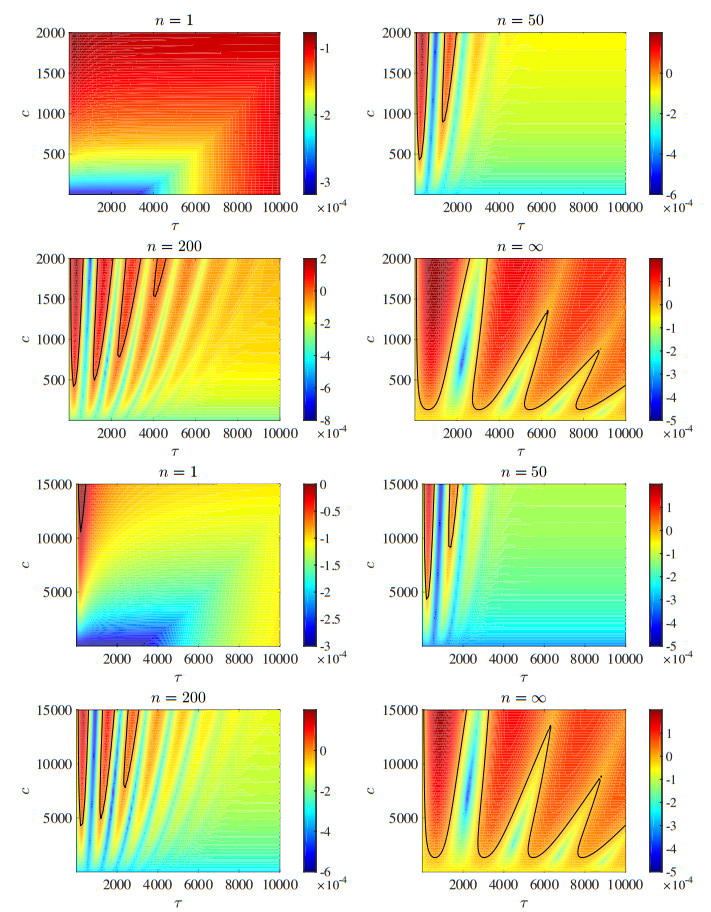
2.4.   Stability charts and other coverage functions

To give a panorama of the situation described at the end of the preceding section, we illustrate in Figure 10 a sketch of the variation of the stability properties of the endemic equilibrium in the $(\tau, c)$-plane as $n$ increases from $1$ to $\infty$, i.e., passing from the case of fading memory Eq (2.5) ($n = 1$, top-left panel) to that of concentrated memory Eq (2.6) ($n = \infty$, bottom-right-panel) through the cases of Erlang distributions Eq (2.7) (intermediate panels). The obtained stability boundaries (through contour in Matlab) denote the presence of so-called stability lobes. In particular, there is only one such lobe for $n = 1$, while more and more lobes appear as $n$ grows, leading to a possibly infinite series of lobes for $n = \infty$. Below these lobes the endemic equilibrium is asymptotically stable, above it becomes unstable in favor of a limit cycle. The latter is stable, at least in proximity of the boundary of the lobe (recall that eigenvalues provide local results). Of course, the stability boundaries represent loci of Hopf bifurcations.

Below we report the results of the same analysis as carried out for different choices of the coverage function $p$ and of the disease prevalence $g$. As for the former and with reference to Eq (2.10), we use the functions of the examples in [27, section 6], i.e., besides Eq (2.11), we consider both the Michaelis-Menten type coverage

and the Holling-type $2$ coverage

where $c_{1}$, $c_{2}$, $d_{1}$ and $d_{2}$ are positive constants. In all cases, $p_{1}$ is (piecewise) smooth and increasing in $M$, $p_{1}(0) = 0$ and $0\leq p_{1}(M)\leq0.99-p_{0}$ ($= c_{i}/d_{i}$, $i = 1, 2$, see [27, section 6]), with an S-shaped profile portraying a slow increase at low levels of $M$ followed by a rapid increase towards saturation. The latter takes into account for the fraction of population that is never reached by vaccination [27, section 2]. Examples of these profiles are given in Figure 11 for $c_{1} = c_{2} = c$, $d_{1} = d_{2} = d$ and $c/d = 1-p_{0}$ with $c = 300$. As for $g$, instead, besides the choice (2.12), we consider also

Figure 12 illustrates the stability charts and boundaries for the choice (2.17) and both cases (2.12) and (2.19) in the same guise of Figure 10, just limiting the choice of values of $n$ to the set $\{1, 50,200, \infty\}$, given that the results are qualitatively unchanged. Figure 13 is the same but for Eq (2.18): Again, the quality of the results is unchanged. The values of the parameters are those described above for Figure 11, except for $c$ which is now varying.

3.   From fading to concentrated memory

In section 2.3 we have seen that by using Eq (2.7) and increasing $n$ starting from $1$, more and more instability intervals due to Hopf bifurcations appear, possibly becoming infinitely-many in the limit as $n\rightarrow\infty$. Here we study the behavior of the relevant rightmost eigenvalues, showing that they converge to those of Eq (2.6) linearly with respect to $n$, i.e., their difference decreases as $O(1/n)$. We thus provide the theoretical confirmation to the experimental results illustrated in Figure 9. Then, in section 4, we show that these results easily extend to models far more general than system (2.3).

The following analysis of convergence is based on the characteristic equations relevant to systems (2.14) and (2.15). The corresponding characteristic functions are compared by applying Rouché's Theorem on zeros of holomorphic functions (see, e.g., ^[36]). By following the arguments used in ^[31], we eventually show that the difference between the eigenvalues of the intermediate case and those of the concentrated case is $O(1/n)$, thus proving also their coincidence in the limit as $n\rightarrow\infty$.

Let us start from the matrix matrix (2.16) at the right-hand side of the linearization of system (2.15) around the endemic equilibrium. The associated characteristic function is

By applying the Laplace rule along the first row we get

Equivalently,

where

and

are analytic functions. Eventually, let us write

for

Now let us look for the characteristic function of the model with concentrated memory, i.e., (2.14). The system linearized at the nontrivial equilibrium $(\overline S, \overline I, \overline M)$ reads

Let $X: = \mathcal{C}([-\tau, 0];\mathbb{R}^3)$ be the state space of the corresponding dynamical system. With reference to ^[34], the associated infinitesimal generator is the linear unbounded operator $\mathcal A:\mathcal{D}(\mathcal{A})\subseteq X\to X$ defined as $\mathcal{A}\varphi = \varphi'$ with domain

for

Since $\lambda\in\sigma(\mathcal A)$ if and only if there exists $\varphi\in\mathcal{D}(\mathcal{A})\setminus\{0\}$ such that $\mathcal A\varphi = \lambda\varphi$, it follows that $\varphi$ satisfies

The unique solution has the form $\varphi(\theta) = e^{\lambda\theta}\varphi(0)$, so that

Therefore, the characteristic function turns out to be

for

coming from Eqs (3.6) and (3.7). Then, by applying Laplace rule along the first row and by using Eqs (3.2) and (3.3), we get

In order to study how $h_{n}$ in Eq (3.1) approaches $h_{\infty}$ in Eq (3.8) as $n\rightarrow\infty$ we need to evaluate their difference for varying $n$. However, thanks to the following lemma, we compare $\overline h_{n}$ in Eq (3.5) with $h_{\infty}$.

Lemma 3.1. If

then $h_{n}(\lambda) = 0\ \Leftrightarrow\ \overline h_{n}(\lambda) = 0$.

Proof. It is enough to observe that condition (3.9) guarantees $f_{2}(-a)\neq0$, so that Eq (3.1) ensures that $\lambda = -a$ cannot be a characteristic root of $h_{n}$. The thesis follows from Eq (3.4). Note that condition (3.9) is satisfied generically when Eq (2.9) holds, given that $n$ is integer.

The following lemmas provide all the ingredients necessary to prove the final convergence result. We denote $\overline B(\lambda, \rho)$ the closed ball in $\mathbb{C}$ of center $\lambda$ and radius $\rho$.

Lemma 3.2 (see Lemma 3.5 in ^[31]). Let $\lambda^{\ast}$ be a zero of $h_{\infty}$ with algebraic multiplicity $m$. Then there exists $\rho_{1} = \rho_{1}(\lambda^{\ast}) > 0$ and $C_{1} = C_{1}(\lambda^{\ast}) > 0$ such that for all $\lambda\in \overline B(\lambda^{\ast}, \rho_{1})\setminus\{\lambda^{\ast}\}$

Proof. By considering the Taylor series of $h_{\infty}(\lambda)$ around $\lambda^{\ast}$ and by taking into account the multiplicity $m$ we obtain $h_{\infty}(\lambda) = h_{\infty}^{(m)}(\lambda^{\ast})(\lambda-\lambda^{\ast})^{m}/m!+O\left(|\lambda-\lambda^{\ast}|^{m+1}\right)$ with $h_{\infty}^{(m)}(\lambda^{\ast})\neq0$. Then $\lim_{\lambda\to\lambda^{\ast}}|h_{\infty}(\lambda)|/|\lambda-\lambda^{\ast}|^{m} = |h_{\infty}^{(m)}(\lambda^{\ast})|m!$. Let us set $C_{1}': = |h_{\infty}^{(m)}(\lambda^{\ast})|/m!$. Since $C_{1}' > 0$, there exists $\rho_{1} > 0$ and $C_{1} > 0$, both depending on $\lambda^{\ast}$, such that, for all $\lambda\in \overline B(\lambda^{\ast}, \rho_{1})\setminus\{\lambda^{\ast}\}$, $|h_{\infty}(\lambda)|/|\lambda-\lambda^{\ast}|^{m} > C_{1}$.

Lemma 3.3. Let $\lambda^{\ast}\in\mathbb{C}$ and $\rho_{0} > 0$. Then there exists $C_{0} = C_{0}(\lambda^{\ast}, \rho_{0}) > 0$ such that for all $\lambda\in \overline B(\lambda^{\ast}, \rho_{0})$ and all $n\in\mathbb{N}\setminus\{0\}$

Proof. Let us fix $z\in\mathbb{C}$ and consider the initial value problem

whose unique solution is $y(t) = e^{zt}$. The proof is based on analyzing the error committed by solving (3.10) with the explicit Euler method with step $h = 1/n$, $n\in\mathbb{N}\setminus\{0\}$. Let $y_{i}$ be the relevant approximation of $y(t_{i})$, $t_{i} = ih$, $i = 1, \dots, n$, and let $y_{0} = y(0)$. The method reads $y_{i+1} = (1+hz)y_{i}$, $i = 0, \dots, n-1$, with $y_{0} = 1$. The local truncation error is $\varepsilon_{i+1}: = (1+hz)y(t_{i})-y(t_{i+1})$, $i = 0, \dots, n-1$, and the second-order Taylor expansion of $y(t_{i+1})$ with Lagrange remainder gives

for some $\xi_{i}\in(t_{i}, t_{i+1})$. The global truncation error at $t_{n} = 1$ follows as

Since $e_{0} = y(0)-y_{0} = 0$, we get $e_{n} = \sum_{i = 0}^{n-1}(1+hz)^{i} \varepsilon_{n-i}$. Then the triangle inequality gives $|e_{n}|\leq\max_{i = 1, \dots, n}|\varepsilon_{i}|\sum_{i = 0}^{n-1}(1+h|z|)^{i}$. The first factor at the right-hand side above is bounded as

As for the second factor we get

thanks to the (left) rectangular quadrature formula for the function $e^{|z|t}$ in $t\in[0, 1]$ with quadrature points $t_{i}$, $i = 0, \dots, n-1$. Therefore $|e_{n}|\leq C'_{0}h$ holds for $C'_{0} = C'_{0}(z): = \frac{1}{2}(e^{|z|}-1)|z|\max\{1, e^{\Re z}\}$. We conclude that $|(1+hz)^{n}-e^{z}| = |e_{n}|\leq C'_{0}/n$ and the thesis follows by choosing $z = \lambda\tau$ and $C_{0} = C_{0}(\lambda^{\ast}, \rho_{0}): = \max_{\lambda\in \overline B(\lambda^{\ast}, \rho_{0})}C'_{0}(\lambda\tau)$.

Lemma 3.4. Let $\lambda^{\ast}\in\mathbb{C}$ and $\rho_{0} > 0$. Then there exists $C_{2} = C_{2}(\lambda^{\ast}, \rho_{0}) > 0$ such that for all $\lambda\in \overline B(\lambda^{\ast}, \rho_{0})$ and all $n\in\mathbb{N}\setminus\{0\}$

Proof. Thanks to Lemma 3.3 there exists $C_{0} = C_{0}(\lambda^{\ast}, \rho_{0}) > 0$ such that $\left(1+\lambda\tau/n\right)^{n} = e^{\lambda\tau}+\gamma(n)$ with $\gamma(n)$ such that $|\gamma(n)|\leq C_{0}/n$. Then $[(1+\lambda\tau/n)^{n}]^{-1} = [e^{\lambda\tau}+\gamma(n)]^{-1} = e^{-\lambda\tau}-e^{-\lambda\tau}\gamma(n)+O(|\gamma(n)|^{2})$ follows by a second-order Taylor expansion. Thus, for all $\lambda\in \overline B(\lambda^{\ast}, \rho_{0})$, $|(1+\lambda\tau/n)^{-n}-e^{-\lambda\tau}|\leq C'_{2}/n$, where $C'_{2}: = C_{0}\cdot\max_{\lambda\in \overline B(\lambda^{\ast}, \rho_{0})}|e^{-\lambda\tau}|$. Now, by Eqs (3.5) and (3.8), we have $|\overline h_{n}(\lambda)-h_{\infty}(\lambda)|\leq\max_{\lambda\in \overline B(\lambda^{\ast}, \rho_{0})}|f_{2}(\lambda)|\cdot|(1+\lambda\tau/n)^{-n}-e^{-\lambda\tau}|$ and the thesis follows by choosing $C_{2} = C_{2}(\lambda^{\ast}, \rho_{0}): = C'_{2}\cdot\max_{\lambda\in \overline B(\lambda^{\ast}, \rho_{0})}|f_{2}(\lambda)|$.

Eventually, we state and prove the convergence of the eigenvalues of $A_{n}$ to those of $\mathcal A$ in terms of zeros of $h_{n}$ and $h_{\infty}$, respectively.

Theorem 3.5 (see Theorem 3.6 in ^[31]). Let $\lambda^{\ast}$ be a zero of $h_{\infty}$ with algebraic multiplicity $m$ and $r > 0$ be such that $\lambda^{\ast}$ is the only zero of $h_{\infty}$ in $\overline B(\lambda^{\ast}, r)$. Then there exists $n^{\ast}\in\mathbb{N}\setminus\{0\}$ sufficiently large such that $h_{n^{\ast}}$ has exactly $m$ zeros $\lambda_{n^{\ast}, 1}, \dots, \lambda_{n^{\ast}, m}$ (counted with multiplicities) in $\overline B(\lambda^{\ast}, r)$ and

with $\rho(n^{\ast}) = O((1/n^{\ast})^{1/m})$.

Proof. Thanks to Lemma 3.2 there exist $\rho_{1} = \rho_{1}(\lambda^{\ast})$ and $C_{1} = C_{1}(\lambda^{\ast}, \rho_{1}) > 0$ such that, for all $\lambda\in \overline B(\lambda^{\ast}, \rho_{1})\setminus\{\lambda^{\ast}\}$, $|h_{\infty}(\lambda)| > C_{1}|\lambda-\lambda^{\ast}|^{m}$. We can assume $\rho_{1} < r$ without loss of generality. Let us define $\rho(n): = [C_{2}/(C_{1}n)]^{1/m}$ for $C_{2}$ as in Lemma 3.4 with $\rho_{0} = \rho_{1}$. Since $\rho(n)\to0$ as $n\to\infty$, there exists $n^{\ast}$ sufficiently large such that $\rho(n^{\ast}) < \rho_{1}$. Then

follows by taking $\lambda\in \overline B(\lambda^{\ast}, \rho_{1})$ such that $|\lambda-\lambda^{\ast}| = \rho(n^{\ast})$. Since both $\overline h_{n}$ and $h_{\infty}$ are holomorphic in $\overline B(\lambda^{\ast}, \rho_{1})$, Rouché's Theorem (see, e.g., ^[36]) ensures that they have the same number of zeros in $\overline B(\lambda^{\ast}, \rho(n^{\ast}))$ counted with multiplicities. The thesis follows by Lemma 3.1.

Remark 3.6. The linear chain trick can be interpreted as a way to approximate a constant delay $\tau$ through a sequence of time steps of constant size $h: = \tau/n = 1/a$. If one thinks about the finite difference scheme corresponding to explicit Euler with step $h$, the bidiagonal matrix of entries $1/h = a$ and $-1/h = -a$ arises naturally, compare with matrix (2.16) or matrix (4.2) below. This translates then into the Taylor's truncation of the exponential function, on which the given convergence proof is indeed based.

4.   A general framework

It is not difficult to realize that the results of the preceding section are independent of the specific model at hands (in our case (2.3)), and thus they can be extended to the much more general modeling setting

as we illustrate next. Above, for $d$ some positive integer, $f:\mathbb{R}^{d+1}\rightarrow\mathbb{R}^{d}$ and $g:\mathbb{R}^{d}\rightarrow\mathbb{R}$ are smooth. Moreover, we assume the existence of a nontrivial equilibrium $(\overline x, \overline M)\in\mathbb{R}^{d+1}$, i.e., $f(\overline x, \overline M) = 0$ for $\overline M = g(\overline x)$. Note that, beyond population models, this setting includes also economic models with time delay, see, e.g., ^[37,38].

Following section 2.3, for $K$ in Eq (2.7) we apply the linear chain trick to obtain the system of $d+n$ ODEs

Linearizing around the nontrivial equilibrium $(\overline x, \overline M)$ gives a linear system with matrix

where the entries have the appropriate dimension. In order to recover the characteristic function it is convenient to partition the characteristic matrix as

with blocks

We can assume the block $D$ to be nonsingular, i.e., $\lambda\neq-a$, in parallel with Lemma 3.2. Therefore its inverse reads

and we can compute the Schur complement

The Schur determinant identity gives then the characteristic function as

where

As for $K$ in Eq (2.6), i.e., in the concentrated case, following section 3 we arrive at the linear delay system

whose characteristic matrix reads

By using the Schur complement of $1$ we obtain the characteristic function as

Now we can apply all the results of section 3, ending up with the same Theorem 3.5 through Lemmas 3.2, 3.3 and 3.4. The latter, in particular, is proved along the same lines just by noting that the determinant is a continuously differentiable function of its argument, so that there exists a constant $C = C(\lambda^{\ast}, \rho_{0})$ such that $|\overline h_{n}(\lambda)-h_{\infty}(\lambda)|\leq C|(1+\lambda\tau/n)^{-n}-e^{-\lambda\tau}|$.

5.   Conclusions

In this paper we extended the stability analysis of ^[27] concerning an SIR model with vaccination at birth, in which the decision to vaccinate depends on the information on the disease. Indeed, we passed from the case of fading memory treated therein to that of concentrated memory through the Erlang distribution with varying shape parameter. The Erlang case is dealt with by using the linear chain trick. We obtained stability charts where it emerges clearly how the number of instability intervals along the delay axis increases to possibly infinitely-many, concluding that delay distributions with lower variance augment the chances of sustained oscillations.

In parallel, we gave a rigorous proof of the linear rate (in terms of the shape parameter) at which the Erlang distribution approaches the Dirac's delta. This is done by analyzing the convergence of the eigenvalues of the variational problems obtained by linearizing the original models around their endemic equilibrium. Moreover, this analysis is showed to be more general than that of the case of the concerned SIR framework.

The above outcomes would not have been obtained without resorting to recent techniques for treating equations with delays, e.g., ^[30,31,32]. We hope that in the future this could serve as a basis to analyze other models involving more or different delays. This would represent indeed an opportunity in view of the many possible directions to extend the modeling of the information term. In particular, it is plan of the authors and colleagues to tackle more realistic memory kernels. Examples can be multimodal distributions, or distributions with unconstrained variance (recall Eq (2.9)), as well as laws of power type or Gaussian-derived kernels. Of course, also going beyond the stability of the endemic equilibrium should be considered, and in this regard we remark that efficient techniques are already available to analyze the stability of periodic behaviors of systems with delays ^[39,40], as well as a more complete bifurcation analysis ^[9].

Acknowledgments

The authors wish to express their gratitude to Bruno Buonomo, Alberto d'Onofrio and Piero Manfredi for several priceless discussions on the subject, which definitely contributed to the draft of this work. AA and DB are members of INdAM Research group GNCS. AA is supported by the PhD program in Computer Science, Mathematics and Physics, University of Udine; DB is supported by the INdAM GNCS project "Approssimazione numerica di problemi di evoluzione: aspetti deterministici e stocastici" (2018) and by the project PSD_2015_2017_DIMA_PRID_2017_ZANOLIN "SIDIA – SIstemi DInamici e Applicazioni" (UNIUD).

Conflict of interest

All authors declare no conflicts of interest in this paper.