Global well-posedness and pattern formations of the immune system induced by chemotaxis

1.   Introduction

Chemotaxis is a directed movement of biological individuals in response to a chemical signal. It is well-known that the chemotaxis can significantly affect the immune system (see ^[1,2]). To be more specific, during the immune process, a chemical which is called chemokine is secreted by the immune cell at sites of inflammation. Then, eukaryotic cells sense the gradient of chemokines by a polarized distribution of receptors, and they move toward relatively high concentrations of the chemical (chemoattraction), or in the opposite direction (chemorepulsion). Thus, chemotaxis seems to be a key contribution to the spatial properties of the solutions to immune systems, such as pattern formations or stabilization.

The immune system is regulated by various immune cells and dysregulation of the immune system is associated with some kinds of diseases. Immunodeficiency occurs when the immune response is less active, whereas hypersensitivity to the immune response is associated with many allergic diseases (see ^[3,4]). There have been several results to analyze the dynamics by using a mathematical model (see ^[5,6,7,8,9]). However, due to many variables and their complex coupling, it is not easy to understand the mechanism mathematically.

In this regard, Lee et al. ^[10] proposed a simplified PDE system involving only three main factors; antigens, chemokines and immune cells. The modelling is motivated by the pioneer work of Keller and Segel ^[11], which studies the aggregation of cellular slime mold toward a higher concentration of a chemical signal. Lee et al. obtained the stability and instability conditions for the uniform steady states and provided numerical observations. In this paper, we investigate the following reaction-diffusion-advection system introduced in ^[10]

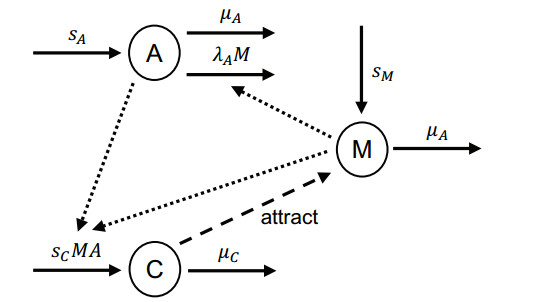
where $\Omega$ is a smoothly bounded domain in $\mathbb{R}^n$, $n = 1, 2$. The unknowns $A$, $C$, and $M$ represent the concentration of antigens, the concentration of chemokines, and the density of immune cells, respectively. Each equation of (1.1) contains a uniform diffusion with a constant coefficient and natural degradation with a constant decay rate. The constant antigen source $s_A > 0$ represents the persistent infection. Since immune cells are produced in bone marrow and circulated throughout the body, we also consider the source of $M$ as a positive constant $s_M > 0$. During the immune process, immune cells and antigens are consumed by regulation and phagocytosis, which are denoted by $\lambda_M MA$ and $\lambda_A MA$, respectively. On the other hand, $s_CMA$ indicates that chemokines are secreted by immune cells depending on the mass of antigens. The chemosensitivity $\chi > 0$ in the advection term contributes to the movement of immune cells toward the gradient of chemokines. For the reader's convenience, we provide Figure 1 introduced in ^[10], which shows interactions between $A$, $C$ and $M$.

We supplement this system with the conditions of nonnegative initial values such that for $p > n$,

and with the homogeneous Neumann boundary conditions

where $\nu$ denotes the outward normal vector to the boundary $\partial \Omega$.

The aim of this work is to verify the global solvability of (1.1)–(1.3) and show the occurrence of pattern formations. The rest of this paper is organized as follows. Section 2 is devoted to show the global existence and uniqueness of classical solutions. In the one-dimensional setting, the existence can be shown without any restriction on $\chi$ or initial conditions. However, in the case of two dimensions, due to the similarity to the minimal Keller-Segel model, the existence can be obtained under a restriction that depends on the initial conditions and coefficients. One of the main theorems (Theorem 2.1) will be followed by some Lemmas and a priori estimates. In Section 3, we present the stability of nonconstant steady states and existence of periodic orbits. Numerical results are given in Section 4. We close the paper in Section 5 with discussions and conclusions.

Throughout this paper, $c$ denotes a positive generic constant which may differ from line to line.

2.   Global existence

In this section, we prove the existence of classical solutions to (1.1). Looking at the first equation of (1.1), we can see that the nonlinear phagocytosis effect $-\lambda_A MA$, due to its negative sign, does not play any role in the blow-up of $A$ and thus $A$ is uniformly bounded in time unless $s_A$ is singular. From the second equation of (1.1), the production of chemokines can not exceed a linear proportional to $M$, and we thereby find a similar structure to the Keller-Segel model. Similarly to $-\lambda_A MA$, the nonlinear regulation $-\lambda_M MA$ in the third equation of (1.1) can not be a crucial obstacle to guarantee the boundedness of $M$. In general, the qualitative properties of the solutions to the minimal Keller-Segel model like boundedness or blow-up phenomena highly depend on the spatial dimension (see ^{[12,13,14,15,16,17]}). For this reason, we shall provide the proofs for each dimension.

2.1.   Preliminaries

First, we introduce some useful estimates related to the heat semigroup (see ^[18,17]).

Lemma 2.1. Let $\{e^{\Delta t}\}_{t\geq0}$ be the heat semigroup in a bounded domain with the homogeneous Neumann boundary condition and let $\lambda_1 > 0$ be the first positive eigenvalue of the Laplace operator $-\Delta$. Then, for any $1\leq q \leq p \leq \infty$, there exists $c = c(p, q, \Omega) > 0$ such that

for all $w\in L^q (\Omega)$;

for all $w\in L^q (\Omega)$.

Next, we assert the local existence of solutions to (1.1) and boundedness of $L^1$-norm. Due to the presence of reaction terms, the total mass is not conservative. But we can still obtain the uniform boundedness of the total mass in time.

Lemma 2.2. Let $\Omega$ be a smooth bounded domain of $\mathbb{R}^n$, $n\geq1$. For any $(A_0, C_0, M_0)$ satisfying (1.2), we have:

(1) There exists a maximal time of existence $T_{\max} > 0$ such that the system (1.1) with (1.3) has a unique nonnegative classical solution satisfying

(2) If $T_{\max} < \infty$, then we have

(3) There exists a positive constant $C_1$ such that

In particular, we have

(4) There exists a positive constant $C_2$ such that

Proof. We let $U = (M, C, A)$ and rewrite (1.1) with (1.2), (1.3) as

where

The real parts of eigenvalues of $A(U)$ are all positive and hence (2.8) is uniformly parabolic. Then, by Amman's well-established parabolic theory introduced in [19, Theorem 7.3] (see also see ^[20,21] for similar approaches), we obtain the local existence, uniqueness of solutions fulfilling (2.3) and blow-up criterion (2.4). The maximum principle ensures the nonnegativity of the solution. More precisely, we observe that the first and third component of $F(U)$ are nonnegative, due to $s_M, s_A > 0$, when $M = 0$, $A = 0$. Then, the nonnegative initial values $(A_0, M_0)$ imply that $(A, M)$ is also nonnegative. From the nonnegativity of $(A, M)$ and the initial value $C_0$, we obtain the nonnegativity of $C$. To show (2.5), we multiply the first equation, the third equation of (1.1) by $s_C$ and the second equation by $\lambda_A+\lambda_M$, respectively, and add them up. Then, integrating the result over $\Omega$ gives

Letting $s_C \int_\Omega A(\cdot, t) + (\lambda_A+\lambda_M) \int_\Omega C(\cdot, t) + s_C \int_\Omega M(\cdot, t) : = y(t)$, we infer from (2.9) that there exist positive constants $c_1$, $c_2$ such that

which guarantees the uniform boundedness (2.5). As to (2.6), we integrate the third equation of (1.1) over $\Omega$ to obtain

Solving the ordinary differential inequality (2.10) with $M_0$, we obtain (2.6). For the last, we consider the following parabolic auxiliary problem for the equation of $A$

Now, we apply (2.1) to the Duhamel formulation of (2.11) as

Then, we have

By the standard comparison principle for parabolic equation (see ^[22]), we obtain

This completes the proof.

2.2.   One dimensional case

In this subsection, we consider an one-dimensional problem. In this case, gradient estimate of $C$ is essential to show the global existence.

Lemma 2.3. Let $n = 1$ and $(A, C, M)$ be a classical solution of (1.1) in $\Omega \times (0, T_{\max})$. Then, we have

where the positive constant $c$ is independent of $T_{\max}$.

Proof. We apply the estimates of Lemma 2.1 to the Duhamel formulation of second equation of (1.1) as the following equation

Using (2.1), (2.6) and (2.7), we deduce from (2.14) that for any $t\in(0, T_{\max})$

where $c$ is independent of $t$ and $\lambda_1$ is the first positive Neumann eigenvalue of the Laplace operator $-\Delta$ on $\Omega$. Since the two integral terms in (2.15) are uniformly bounded in $t$, this completes the proof.

The boundedness of $\|M\|_{L^p}$ follows from (2.13).

Lemma 2.4. Let $n = 1$, $p > 1$ and $(A, C, M)$ be a classical solution of (1.1) in $\Omega \times (0, T_{\max})$. Then, we have

where the positive constant $c$ depends on $p$.

Proof. Testing the last equation of (1.1) by $M^{p-1}$ for any $p > 1$, we have

Using (2.13), the Gagliardo-Nirenberg inequality, and Hölder's inequality, we compute

where $c_3$ and $c_4$ are positive constants independent of $p$. Combining (2.17) and (2.18), we see that

where $c_5 = c_4 + 1$. Note from the Gagliardo-Nirenberg inequality and (2.6) that

holds for some positive constants $c_6, c_7, c_8$ and $\theta_1 = \frac{p/2-1/2}{p/2+1/2}\in(0, 1)$. Plugging (2.20) into (2.19), we obtain

where $c_9 = (p-1)s_M^p |\Omega| + \frac{2D_M(p-1)}{p}$. Since $\frac{1}{\theta_1} > 1$, by a standard ODE comparison, we conclude that

where the positive constant $c$ depends on $p$.

By the application of bootstrap arguments, we prove the uniform boundedness of $A$, $C$ and $M$ as desired.

Lemma 2.5. Let $n = 1$ and $(A, C, M)$ be a classical solution of (1.1) in $\Omega \times (0, T_{\max})$. Then, we have

where the positive constant $c$ is independent of $T_{\max}$.

Proof. Let $0 < T < T_{\max}$. The boudnedness of $A$ for $t\in(0, T)$ is a direct consequence of (2.7). As to the estimate of $C$, applying the estimates of Lemma 2.1 to (2.14) with (2.7) and (2.16), we have for any $p > 1$

where $c$ is independent of $T$. Now, we apply the Moser-Alikakos iterative technique ^[23] to show the boundedness of $M$. Adding $p^3(p-1)\int_{\Omega}M^p dx$ to the both sides of (2.19), we have

where $c_{10} = c_5 +1$. Interpolation inequality entails

where $c_{11}$ is a positive constant independent of $p$. Therefore, (2.21) turns into

We integrate (2.22) in time to obtain

where $c_{12}$ is a positive constant independent of $p$. We define

Thus, we rewrite (2.23) as

where $c_{13}$ is a positive constant independent of $p$. Taking $p = 2^i$, $i = 1, 2, \cdots,$ we have

where $c_{14} = c_{13} 2^{4\sum_{j = 1}^{\infty}\frac{j}{2^{j}}}$. Letting $i\rightarrow \infty$, we have

where $c_{14}$ is independent of $t$. Since $T < T_{\max}$ is arbitrary, we complete the proof.

2.3.   Two dimensional case

In this subsection, we deal with the case of two spatial dimensions. First, we derive the uniform boundedness of $\| M \log M\|_{L^1(\Omega)}$ and $\|\nabla C\|_{L^2(\Omega)}$under a smallness condition on $M_1$. When the total mass of $M$ is conserved, a Lyapunov functional is a helpful tool to prove the global existence (see ^[15]). However, due to reaction terms, the construction of a Lyapunov functional for this problem is very challenging. Instead, we use the Poincare inequality and the Cauchy-Schwarz inequality.

Lemma 2.6. Let $n = 2$ and $(A, C, M)$ be a classical solution of (1.1) in $\Omega \times (0, T_{\max})$. Then, for a sufficiently small $M_1$, we have

where the positive constant $c$ is independent of $T_{\max}$.

Proof. Testing the third equation of (1.1) by $\log M$, the integration by parts implies

where we used Young's inequality. Using (2.7), we find that there exists a positive constant $c_{15} > 0$ such that

Thus, (2.25) turns into

where we used the inequality $x - \log x > 0$ for $x > 0$. On the other hand, we test the second equation of (1.1) by $-\Delta C$ to obtain

Combining (2.26) and (2.27), we have

Adding $(2\mu_C - \mu_M)\int_\Omega M\log M$ to the both sides of (2.28), we obtain

If $\mu_M \leq 2\mu_C$, then (2.29) turns into

For the other case $\mu_M > 2\mu_C$, due to the positive uniform bound of $-x\log x$ for $x > 0$, we find a positive constant $c_{16}$ such that

Now letting $M_{ave}(t): = \frac{1}{|\Omega|}\int_\Omega M(\cdot, t)$, the Poincare inequality gives

where $c_\Omega$ is a positive constant satisfying

By the Cauchy-Schwarz inequality, we deduce from (2.32) that

Plugging (2.33) into (2.30) or (2.31), it follows from (2.6) that

for some $c_{17}, c_{18} > 0$. Note that $c_{17}$ depends on $\chi$ and it is independent of $M_1$, whereas $c_{18}$ depends on $M_1$. Therefore, if $M_1$ is sufficiently small so that $M_1^2 \leq \frac{D_M}{C_{17}}$, then (2.31) ends up with

Solving this inequality directly, we completes the proof.

Thanks to the work done by Bellomo et al. ^[24], the boundedness of $\int_\Omega M \log M$ and $\int_\Omega |\nabla C|^2$ are sufficient to obtain the global existence.

Lemma 2.7. Let $n = 2$ and $(A, C, M)$ be a classical solution of (1.1) in $\Omega \times (0, T_{\max})$. Then, for the same assumption on $M_1$ as in Lemma 2.6, we have

where the positive constant $c$ is independent of $T_{\max}$.

Proof. Detailed proofs can be found in [24,Lemma 3.3].

Now, we are in position to prove our first main theorem which gives the existence of a global-in-time classical solution to (1.1) for $n = 1, 2$.

Theorem 2.1. Let $\Omega$ be a smooth bounded domain of $\mathbb{R}^n$. If $n = 1$ or $M_1$ is sufficiently small for $n = 2$, then, the system (1.1)–(1.3) possesses a unique global-in-time nonnegative uniformly bounded classical solution $(A, C, M)$ in $\Omega \times (0, \infty)$ such that

Proof. Suppose that $T_{\max} < \infty$. According to Lemma 2.5 and Lemma 2.7, there exists $c > 0$ such that

where $c$ is independent of $T_{\max}$. This is contrary to Theorem 2.2 which implies $T_{\max} = \infty$. We complete the proof.

3.   Stability and bifurcation

In this section, we analyze the bifurcation of the system (1.1). For simplicity, we consider the one-dimensional case :

where the domain length $L$ is a positive constant. Recalling the work in ^[10], we find that the system (1.1) has the unique positive equilibrium $(\mkern 1.5mu\overline{\mkern-1.5mu{A}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{C}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{M}\mkern-1.5mu}\mkern 1.5mu)$ such that

where

We the following functions spaces:

From the equilibrium (3.2), we can rewrite the system (3.1) in the following abstract form:

where $z(x, t) = (a, c, m) : = (A - \mkern 1.5mu\overline{\mkern-1.5mu{A}\mkern-1.5mu}\mkern 1.5mu, C - \mkern 1.5mu\overline{\mkern-1.5mu{C}\mkern-1.5mu}\mkern 1.5mu, M - \mkern 1.5mu\overline{\mkern-1.5mu{M}\mkern-1.5mu}\mkern 1.5mu)$, and $\mathcal{L}_\chi : H_1 \rightarrow H$, $G_\chi : H_1 \rightarrow H$ satisfy

To obtain the principle of exchanging stability, we focus on the linearized system of (3.3)

Now, we express $z = (a, c, m)$ as

and then the linearized system (3.4) is equivalent to the following eigenvalue problem:

where $\mathcal{M}_k$ is a $3 \times 3$ matrix such that

The principle of exchanging stability is determined by the sign of eigenvalues of each $\mathcal{M}_k$, and we have the following proposition (see [10, Lemma 1]).

Proposition 3.1. The equilibrium $(\mkern 1.5mu\overline{\mkern-1.5mu{A}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{C}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{M}\mkern-1.5mu}\mkern 1.5mu)$ of (3.1) is locally asymptotically stable if $\chi < \chi_c = \min_{k \geq 1} \{\chi_k^S, \chi_k^H\}$ and it is unstable if $\chi > \chi_c$, where

with

Proof. Let $\Lambda_k^1$, $\Lambda_k^2$, and $\Lambda_k^3$ be eigenvalues of $\mathcal{M}_k$. By the Routh-Hurwitz criterion, $\text{Re}\Lambda_k^i < 0$ for all $k = 1, 2, 3, \cdots$ and $j = 1, 2, 3$ if and only if

where

Then, one can easily check that (3.9) completes the proof. The details can be found in [10,Lemma 1].

3.1.   Pitchfork bifurcation

In this section, we examine the nonconstant steady state solution to (3.1) when $\chi_c = \min_{k \geq 1}\chi_k^S < \min_{k \geq 1} \chi_k^H$. Then, there exists $k_0\geq1$ such that $\chi_{k_0}^S = \chi_c$. Let $\Lambda_k^1(\chi)$, $\Lambda_k^2(\chi)$ and $\Lambda_k^3(\chi)$ be the eigenvalues of $\mathcal{M}_k$ with $\text{Re}\Lambda_k^1(\chi) \geq \text{Re}\Lambda_k^2(\chi) \geq \text{Re}\Lambda_k^3(\chi)$. Then, $\Lambda_{k_0}^1(\chi)$ is the first real eigenvalue of (3.1) which changes its stability at $\chi = \chi_c$, i.e., we have

By Proposition 3.1, the system (3.1) bifurcates from the equilibrium $(\mkern 1.5mu\overline{\mkern-1.5mu{A}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{C}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{M}\mkern-1.5mu}\mkern 1.5mu)$ to another steady state solution as $\chi$ increases passing through $\chi_c$. Before we state the theorem of steady state bifurcation below, we introduce the following parameter $K_3$:

where

and $\psi(x) = (\psi_1(x), \psi_2(x), \psi_3(x)) \in H_1$ satisfies

with

Theorem 3.1. Let $\chi_{k_0}^S = \min_{k \in \mathbb{N}} \chi_k^S < \min_{k \in \mathbb{N}} \chi_k^H$ for some $k_0\in\mathbb{N}$, and let $K_3$ be given as in (3.11). Suppose that $\chi > 0$ satisfies $\chi > \chi_{k_0}^S$. If $K_3 > 0$, then there exist two bifurcated solutions $z^\chi_{\pm} = (a^\chi, c^\chi, m^\chi)^T$ to (3.1), which are attractors. Moreover, $z^\chi_{\pm}$ can be expressed as

where $\xi_{k_0}^1$ is given as in (3.13). And if $K_3 \leq 0$, then there are no bifurcated solutions.

Proof. We use a similar method introduced in [25,Theorem 4.2] based on the center manifold theory (see e.g., ^[26]). Let $\Phi$ be the center manifold function of the equation (3.3) at $\chi = \chi_c$. Since $\mathcal{M}_{k_0}|_{\chi = \chi_c}$ has a simple zero eigenvalue with the eigenvector $\xi_{k_0}^1$ in (3.14), we can express $z$ as

and the equation (3.3) is decomposed as the following:

where $P_1 : H \rightarrow \text{span}\{z_{k_0}^1 \} \subset H$ and $P_2: H \rightarrow \text{span}\{z_{k_0}^1 \}^\perp$ are the natural projections. Then the bifurcation type of the equation (3.3) completely depends on the first equation of (3.15). Let $z_{k_0}^{1*} = \xi_{k_0}^{1*} \cos \frac{k_0 \pi x}{L}$, where $\xi_{k_0}^{1*}$ is the eigenvector of $\mathcal{M}_{k_0}^*|{\chi = \chi_c}$ corresponding to the zero eigenvalue. Taking the $H$-inner product to the both sides of the first equation of (3.15) by $z_{k_0}^{1*}$, we can get the following equation:

where $(\cdot, \cdot)$ denotes the $H$-inner product. Since we consider $\chi$ near $\chi_{k_0}^S$, $G_\chi$ can be approximated by $G_{\chi_{k_0}^S}$. Due to the form of $G_{\chi_{k_0}^S}$ and $\Phi(yz_{k_0}^1) = O(y^2)$ (see ^[26]), we can express $g$ as

Direct calculations yield that

which has the factor $\int_0^L \cos^3 \frac{k_0 \pi x}{L} dx = 0$. To calculate $K_3$, we let

with $u = (u_1, u_2, u_3)^T$ and $v = (v_1, v_2, v_3)^T$. Then, we can write $G_{\chi_{k_0}^S}(z) = G_2(z, z)$. Since $\Phi(yz_{k_0}^1) = O(y^2)$, we have

and, with the aid of Theorem A.1.1 in ^[26], $\Phi$ satisfies $\mathcal{L}_\chi \Phi = - P_2 G_{\chi_{k_0}^S}(y z_{k_0}^1)$. Note that $G_{\chi_{k_0}^S}(yz_{k_0}^1) \in \text{span}\{z_{k_0}^1 \}^\perp = \{w \in H|(w, z_{k_0}^{1*}) = 0 \}$ because $\int_0^L \cos^3 \frac{k_0 \pi x}{L} dx = 0$. Therefore, $\psi$ satisfies (3.12) and we have

which is calculated as in (3.11). Hence, the system (3.1) has a pitchfork type bifurcation and we complete the proof as desired.

3.2.   Hopf bifurcation

In this subsection, we consider the case $\chi_c = \min_{k \geq 1}\chi_k^H < \min_{k \geq 1} \chi_k^S$, which may give rise to the existence of periodic solutions. Let $k_1$ be the positive integer satisfying $\chi_{k_1} = \chi_c$. Then, there exists at least one eigenmode $k$ such that $\chi_k^H < \chi_k^S$. Recalling from Lemma 1 in ^[10], we calculate the characteristic polynomial of $\mathcal{M}_k$ as $\Lambda^3 + P_k \Lambda^2 + (Q_{k, 0} - \chi Q_{k, 1})\Lambda + (R_{k, 0} - \chi R_{k, 1})$ with $P_k$, $Q_{k, 0}$, $Q_{k, 1}$, $R_{k, 0}$ and $R_{k, 1}$ given in (3.8). By the Routh-Hurwitz criterion, for a such mode $k$ with $\chi_k^H < \chi_k^S$ and the choice of $\chi = \chi_k^H$, $\mathcal{M}_k$ has two pure imaginary and one negative eigenvalues:

To obtain the existence of the Hopf bifurcation, we apply the bifurcation theory from ^[27] and we check the transversality condition. The similar proof can be found in [28,Theorem 3.1].

Theorem 3.2. Let $\min_{k \in \mathbb{N}} \chi_k^H < \min_{k \in \mathbb{N}} \chi_k^S$. For each $k \in \mathbb{N}$, we suppose that $0 < \chi_k^H < \chi_k^S$ and $\chi_j^H \neq \chi_k^H$ for any $j \neq k$, $j\in\mathbb{N}$. Then, there exist $\delta > 0$ and a unique one-parameter family of nontrivial periodic orbits $\rho_k(s) = \left(z_k(s, x, t), T_k(s), \chi_k(s)\right) : s \in (-\delta, \delta) \rightarrow C^3(\mathbb{R}, H_1) \times \mathbb{R}^+ \times \mathbb{R}$ satisfying $\left(z_k(0, x, t), T_k(0), \chi_k(0)\right) = \left(0, \frac{2\pi}{\zeta_k}, \chi_k^H\right)$ and

such that $(z_k(s), \chi_k(s))$ is a nontrivial solution of (3.3) and $z_k(s)$ is periodic with period $T_k(s) \approx \frac{2\pi}{\zeta_k}$ where $\zeta_k = \sqrt{Q_{k, 0} - \chi_k^H Q_{k, 1}}$ and $\xi_k^{1, 2}$ are the eigenvectors of $\mathcal{M}_k|_{\chi = \chi_k^H}$ corresponding to $\Lambda_k^{1, 2}(\chi_k^H)$. Moreover, $\rho_k(s_1) \neq \rho_k(s_2)$ for all $s_1 \neq s_2$, $s_1, s_2 \in (-\delta, \delta)$ and all nontrivial periodic solutions of (3.3) around $(0, \chi_k^H)$ must be on the orbit $\rho_k(s)$ in the sense that, if (3.3) has a periodic solution $\tilde{z}(x, t)$ with period $T$ for some $\chi \in \mathbb{R}$ around $\rho_k(s)$ such that for small $\epsilon > 0$ $|\chi - \chi_k^H| < \epsilon$, $|T-2 \pi/ \zeta_k | < \epsilon$ and $max_{ t > 0, x \in [0, L] } |\tilde{z}(x, t)| < \epsilon$, then there exist numbers $s \in (-\delta, \delta)$ and some $\theta > 0$ such that $(T, \chi) = (T_k(s), \chi_k(s))$ and $\tilde{z}(x, t) = z_k(s, x, t+ \theta)$.

Proof. The proof is based on Theorem 1.11 in ^[27]. Consider the case of an eigenmode $k\in \mathbb{N}$ with $\chi_k^H < \chi_k^S$. Since the diffusion coefficients $D_A$, $D_C$ and $D_M$ are all positive, the system (3.3) is normally parabolic. Also since $\chi_k^H \neq \chi_j^H$ for all $k \neq j$, $k, j \in \mathbb{N}$, the matrix $\mathcal{M}_k|_{\chi = \chi_k^H}$ has no eigenvalues of the form $iN \zeta_k$ for $N \in \mathbb{Z} - \{-1, 1\}$, and by the Routh-Hurwitz criterion, 0 is not an eigenvalue of $\mathcal{M}_k|_{\chi = \chi_k^H}$.

Let $\Lambda_k^{1, 2}(\chi) = \eta(\chi) \pm i \zeta(\chi)$ and $\Lambda_k^3(\chi)$ be the eigenvalues of $\mathcal{M}_k$ with $\chi$ around $\chi_k^H$. To complete the proof, we check the following transversality condition

By the relation between the roots and coefficients of the caracteristic equation of $\mathcal{M}_k$, we obtain that

Differentiating the above equations with respect to $\chi$, we obtain that

and

Since $\eta(\chi_k^H) = 0$ and $\Lambda_k^3(\chi_k^H) = - P_k$, we solve (3.21) with $\chi = \chi_k^H$ to obtain

so that $\eta'(\chi_k^H) = - \frac{1}{2} \Lambda_k^3{'}(\chi_k^H) > 0$. This completes the proof.

4.   Numerical simulations

In this section, we provide numerical examples of stable and time-periodic solution to the system (3.1) for the one dimensional case. We use the upwind finite volume scheme introduced in ^[29,30]. The parameter sets are given in Table 1 introduced in ^[10]. Since the model is simplified, it is not easy to find all the parameters estimated from the experiments. The diffusion coefficients and decay/death rates are usually known (see ^[31,9] and references therein). For example, the diffusion coefficient $D_M$ is estimated in a range of $10^{-11}$–$10^{-7} cm^2/h$ (see ^[32]). In this work, we choose $D_M = 5\times 10^{-7}cm^2/h$ in the range. We choose domain length $L = \text{(half of some integers)} \times 0.005m$, which is relevant to contain a sufficient number of cells considering the size of the cells.

4.1.   Nonconstant stable steady states

By direct computations with (3.2) and Proposition 1, we obtain a positive constant equilibrium $(\mkern 1.5mu\overline{\mkern-1.5mu{A}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{C}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{M}\mkern-1.5mu}\mkern 1.5mu) \approx (1.86 \times 10^{-2}, 1.93 \times 10^{-5}, 2.59 \times 10^{-1})$ and $Q_{k, 0}R_{k, 1} > Q_{k, 1}R_{k, 0}$ for all $k \in \mathbb{N}$, which implies that $\chi_k^S < \chi_k^H$ for all $k \in \mathbb{N}$.

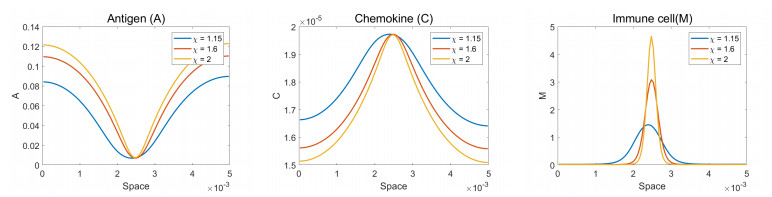
First we observe the chemotactic effect in a fixed domain length $L = 0.005$ with varying $\chi$. In this case, we have $\min_{k \in \mathbb{N}}\chi_k^S = \chi_2^S \approx 1.097$. Thus, if we choose $\chi > 1.097$, then the system bifurcates from the equilibrium to another stable steady state solution. In Figure 2, we illustrate steady state solutions of $A$, $C$ and $M$ with $\chi$ taken to be 1.15, 1.6 and 2. We see that $A$ has an interior spike, and $C$ and $M$ have boundary layers on each boundary. As $\chi$ increases, the solutions become more aggregated.

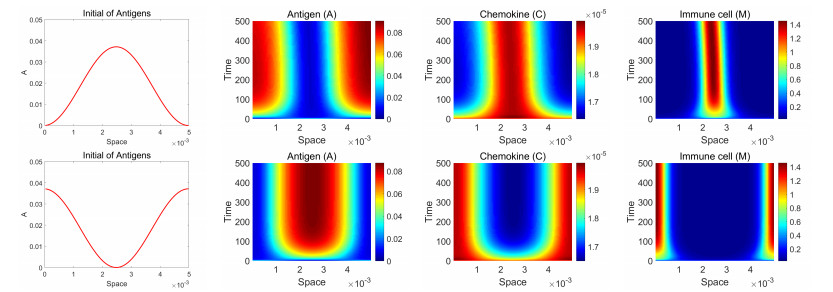
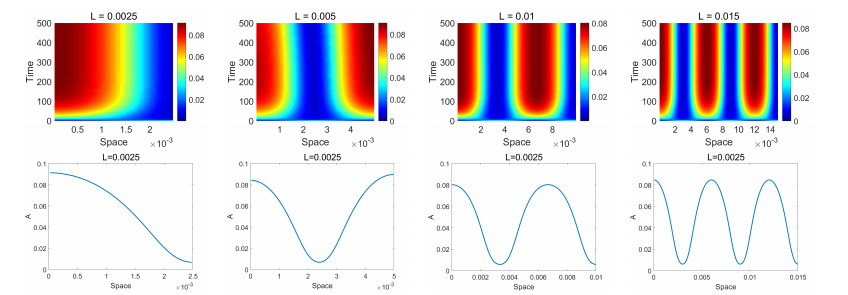
In Figure 3, there are two steady state solutions with different structures. Theorem 3.1 indicates that the system (3.1) has two bifurcated stable steady solutions in case of $\chi_c = \min_{k \in \mathbb{N}}\chi_k^S < \min_{k \in \mathbb{N}}\chi_k^S$. Figure 3 shows that the structure of bifurcated solutions depends on the initial condition. Figure 4 illustrates the simulation in several cases of domain lengths, $L = 0.0025, \; 0.005, \; 0.01, \; 0.015$, and for each case, $\chi = 1.2, \; 1.15, \; 1.07, \; 1.065$ are chosen. We see from Table 2 that the stable steady solutions have the profile $\cos \frac{k_0 \pi x}{L}$ when $\chi$ is slightly bigger than $\chi_{k_0}^S = \min_{k \in \mathbb{N}}\chi_k^S$. These numerical results in Figure 3 and 4 agree with the theoretical results of Theorem 3.1.

4.2.   Time-periodic solutions

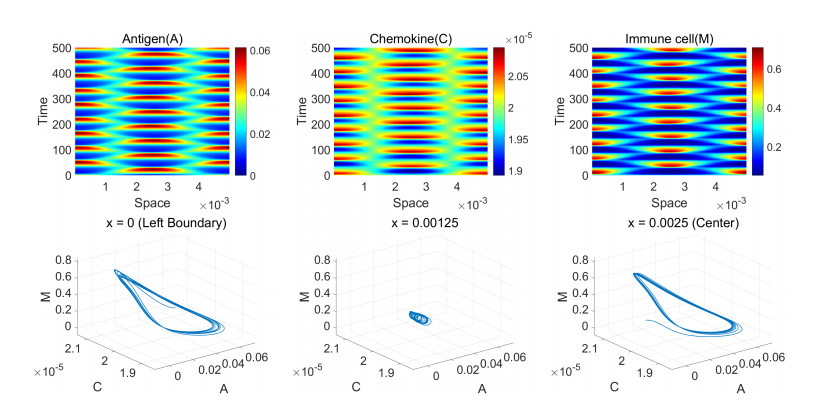
From Table 1, we find the positive constant equilibrium $(\mkern 1.5mu\overline{\mkern-1.5mu{A}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{C}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{M}\mkern-1.5mu}\mkern 1.5mu) = (2.00 \times 10^{-2}, 2.00 \times 10^{-5}, 2.50 \times 10^{-1})$ and $\min_{k \in \mathbb{N}}\chi_k^H \approx 1.04 < \min_{k \in \mathbb{N}}\chi_k^S \approx 14$. In this case, by Theorem (3.2), the system (3.1) posseses time-periodic solutions.

Figure 5 illustrates time-periodic solutions to (3.1) with parameters of Table 1 and $L = 0.005$ when $\chi = 1.085$ is chosen slightly bigger than $\min_{k \in \mathbb{N}} \chi_k^H = \chi_2^H \approx 1.08$. Letting $\zeta_k(\chi) = \sqrt{Q_{k, 0} - \chi Q_{k, 1}}$, we compute the period of the solution as $T = \frac{2 \pi}{\zeta_k(\chi_2^H)} \approx 49.2$. Figure 6 shows the spatial profile of time periodic solutions featuring $\cos \frac{k_1 \pi x}{L}$, where $k_1 = \text{argmin}_{k \in \mathbb{N}}\chi_k^H$ for varying domain size $L = 0.0025, \; 0.005, \; 0.01, \; 0.0125$. Then, $k_1$ and $\chi_{k_1}^H = \min_{k \in \mathbb{N}}\chi_k^H$ are given in Table 3.

5.   Conclusions and discussions

In this paper, we investigate the global solvability and bifurcation dynamics of the system (1.1) with the boundary condition (1.3) introduced in ^[10]. The system (1.1) has a minimal type of chemotactic sensitivity, i.e., constant $\chi = \text{const}$. Due to a similar structure to the classical Keller-Segel model (see ^[11]), the global solvability of the problem depends on the dimension. In the one dimensional case, the global existence and uniform boundedness of solutions can be proved for any $\chi > 0$. However, in the two dimensional case, the global solvability of this model is obtained under smallness assumptions (see ^[15] for Keller-Segel model case).

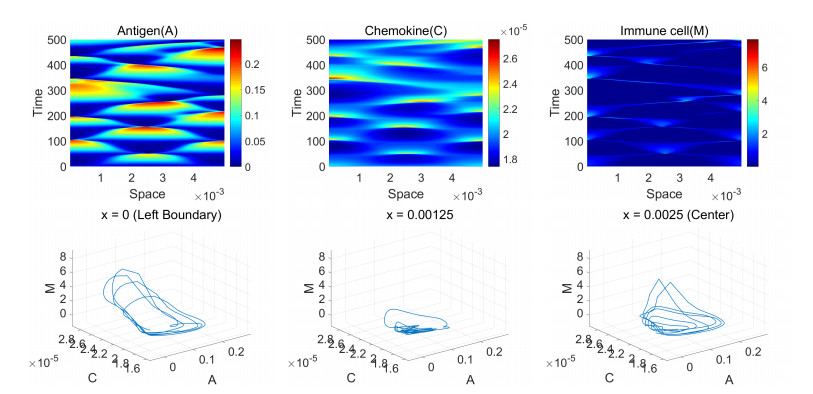
In view of the stability analysis, it is known that the system has a single positive constant equilibrium $(\mkern 1.5mu\overline{\mkern-1.5mu{A}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{C}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{M}\mkern-1.5mu}\mkern 1.5mu)$ described in (3.2) and there exists a threshold $\chi_c = min_{k \in \mathbb{N}} \{\chi_k^S, \chi_k^H\}$ of $\chi$ such that the equilibrium $(\mkern 1.5mu\overline{\mkern-1.5mu{A}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{C}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{M}\mkern-1.5mu}\mkern 1.5mu)$ is asymptotically stable when $\chi < \chi_c$ and unstable when $\chi > \chi_c$ (see ^[10]). This study goes further from the work in ^[10] by means of local bifurcation theory. As $\chi$ increases passing through the threshold value $\chi_c$, the equilibrium $(\mkern 1.5mu\overline{\mkern-1.5mu{A}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{C}\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu{M}\mkern-1.5mu}\mkern 1.5mu)$ becomes unstable and two different type bifurcated solutions can occur; If $\chi_{k_0}^S < \chi_k^H$ for all $k \in \mathbb{N}$, then there exist nonconstant steady states whose structure depends on initial values, and if $\chi_{k_1}^H < \chi_k^S$ for all $k \in \mathbb{N}$, then we obtain time-periodic solutions. Moreover, we obtain the information of wave modes of bifurcated solutions in both cases. However, in Hopf bifurcation case, the information of wave modes is local which means that the solution can have different dynamics from the form of (3.18) when $\chi$ is much bigger than $\chi_c = \chi_{k_1}^H$. We see this dynamics, via the example illustrated in Figure 7. The global bifurcation will be investigated in the future.

Acknowledgments

Authors greatly appreciate valuable comments and suggestions of the anonymous reviewer of this paper. H. J. Hwang was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF- 2017R1E1A1A03070105 and NRF-2019R1A5A1028324). Changwook Yoon was supported by National Research Foundation of Korea (NRF) grants funded by the Korea government (MSIP) (NRF-2017R1E1A1A03070652 and NRF-2017R1D1A1B03031035).

Conflict of interest

The authors declare that they have no competing interests.