1. Introduction
The importance of the housing market to the wider economy has been well documented in empirical research with a number of studies noting,
inter alia, its substantive contribution to private sector wealth, dominance over the stock market in determining household consumption decisions, central role within the macroeconomy and close relationship with economic fundamentals (Brueckner, 1997; Holly and Jones, 1997; Gallin, 2006; Goetzmann, 1993; Goodhart and Hoffman, 2007; Bayer et al., 2010; Costello et al., 2011; Case et al., 2013; Han, 2013). As a consequence, the behaviour of housing markets and the properties of house prices have received much attention. In recent years, one element of this research has considered whether housing displays the risk-return characteristics predicted for other financial assets by standard finance theory. A feature of this literature is the repeated discussion of the existence of a counterintuitive negative risk-return relationship within housing markets (Dolde and Tirtiroglu, 1997; Morley and Thomas, 2011; Han, 2013; Lin and Fuerst, 2014). Clearly this runs contrary to the positive risk-return relationship depicted by theoretical finance where higher risk is compensated by higher returns.
The contribution of the present paper to the existing literature is twofold. First, previous research is extended by producing the first findings on this issue for the highly topical London housing submarket. Second, an explicit investigation is provided of the extent to which decisions regarding empirical design impact upon inferences concerning risk and return in housing markets. More precisely, the present research considers the influence of the components of empirical design upon the subsequent inferences drawn by investigators when examining the relationship between risk, as measured by volatility, and returns. Consequently, it is examined how the significant negative relationship which has featured so prominently in the literature is dependent upon stances taken with regard to decisions on variable definition, sample selection, optimisation methods, dynamic specification, regional disaggregation and modelling techniques. Interestingly the results of the current analysis show that while negative risk-return relationships are observed for an empirical design with very specific options selected for the sample, modelling technique and approach to dynamic specification employed, a more thorough analysis produces mixed findings.
To achieve its objectives, this paper will proceed as follows. In Section 2 a selected review of the literature on the analysis of volatility and risk in housing markets is presented. The various components of the empirical design employed to examine risk and return in the present analysis are provided in Section 3, with the empirical results from this analysis presented in Section 4. Section 5 provides some concluding remarks.
2. Literature Review
In this section a selected review of the literature in relation to the analysis of volatility and risk in housing markets is provided. Considering these two issues in turn, house price volatility has received much attention in the empirical literature for a number of years, as illustrated by, Foster and Van Order (1984), Crawford and Rosenblatt (1995), Dolde and Tirtiroglu (1997), Crawford and Fratantoni (2003), Miller and Peng (2006), Miles(2008, 2011), Miller and Pandher (2008), Morley and Thomas (2011) and Barros et al. (2015). However, while a wealth of empirical studies have emerged examining volatility, the development of theoretical explanations for its presence have received less attention with the inertia-based explanation of Case and Shiller(1988, 1989, 1990) and Wheaton's (2015) decomposition of volatility into demand-and supply-side factors being notable exceptions to this. Inspection of the empirical literature examining volatility shows the use of the autoregressive conditional heteroskedasticity (ARCH) model and its various extensions to feature prominently. Interestingly, it can be seen that their use has produced conflicting results. As an illustration of this, while Dolde and Tirtiroglu (1997), Crawford and Fratantoni (2003) and Miles (2008) present evidence of volatility in house prices for the USA, the results of Miller and Peng (2006) are less supportive. Similarly, the results of Miles (2011) suggest an element of volatility in UK house prices with just over half of the regions considered providing evidence of significant volatility, the evidence provided by Lin and Fuerst (2014) is more compelling for Canada.
With regard to 'risk', a number of differing perspectives have been adopted in the literature to consider its both is presence and its impact. Portfolio risk management provides the motivation for both Huang et al. (2016) and Zhou and Gao (2012). While Huang et al. (2016) consider the management of risk via diversification in real estate investment trust (REIT)-housing and stocks-housing portfolios, Zhou and Gao (2012) employ copula-based methods to explore risk management in real estate securities. A further alternative consideration of the role of risk in housing markets is provided by Tsang et al. (2016) where stochastic dominance analysis is employed to examine the impact of risk on housing purchase decisions in the Hong Kong market. Additional research more closely related to the present analysis is provided by Domian et al. (2015) where two specifications of CAPM are employed to consider the risk-return relationship across Metropolitan Statistical Areas (MSAs) in the USA using the Case-Shiller house price index. Extending the analysis to include leverage and liquidity risks, Domian et al. (2015) provide evidence of geographical variation across MSAs with counter-cyclical behaviour noted in some areas such as cities in Californian contasting with the higher levels of risk noted in, for example, New York. However, the literature on the risk-return relationship in housing is dominant by the use of ARCH-based models which are employed in the current analysis. Specific examples of this include Dolde and Tirtiroglu (1997), Morley and Thomas(2011, 2016), Lin and Fuerst (2014) and Lee (2017). As noted by Han (2013) and in the studies above, a negative relationship between risk and returns has been noted in this literature. This variation in the sign of the risk-return relationship and its possible dependence on the nature of the approach adopted towards modelling provides the motivation for the current study. To explore this issue and provide an extension to the existing literature, the current analysis explicitly considers the impact of variations in the empirical design of econometric framework upon the results obtained with regard to the risk-return relationship.
3. Risk-return and the Housing Market
In this section the structure, or components, of the empirical analysis are outlined. The material is structured via consideration of the decisions made concerning variable definition, sample selection, modelling techniques and dynamic specification when undertaking an analysis of risk and return. Typically these decisions and assumptions are implicit (or unrecognised) when performing empirical analysis. In contrast, the present research makes explicit the alternative options available to investigators in the process of moving from an initial hypothesis of interest motivating empirical analysis to the testable framework from which inferences are drawn.
3.1. Data
To consider the nature of risk and return within housing markets, an obvious issue to consider concerns the actual series to be examined. In the present analysis, the London housing market is considered. The London housing market is a highly topical example receiving frequent attention within both academia and the media, and hence an attractive choice. The specific series considered herein are those for the 32 boroughs of London plus the aggregate London series. The house price data considered are monthly, seasonally adjusted observations on average house prices in the over the period January 1995 to December 2015.* While the London submarket has been examined recently by Abbott and De Vita (2012), the data set employed in the present analysis differs from that employed in their examination of housing market convergence. First, the aggregate London price series considered here was not considered by Abbott and De Vita (2012). Second, the 32 boroughs of London are considered herein without the addition of the City of London local authority district.† Third, in a further departure from the previous study, the house price series are considered in nominal terms as well as in real (inflation adjusted) terms following deflation using the consumer price index. Consideration of both nominal and real data recognises the common use of real data in analysis of risk and return, along with the argument within the economics literature that decision making is often undertaken by consideration of nominal values (Shafir et al., 1997). ‡ Fourth, the sample considered differs from that employed by Abbott and De Vita (2012) as it is observed at a monthly, rather than quarterly frequency, with this higher frequency allowing an improved analysis of volatility. Finally, seasonally adjusted, rather than unadjusted, observations are considered for a sample which starts a year earlier and finishes over 6 years later than that of Abbott and De Vita (2012). As a result, the current analysis considers a sample of 252 observations compared to 54 in Abbott and De Vita (2012). Therefore, despite initially appearing similar, the data in the current analysis differ markedly from those in Abbott and De Vita (2012) due to sample span, number of observations, frequency, seasonal adjustment, aggregation and the nominal/real measurement dichotomy. Importantly, the presence of these options illustrates the relevance of the issue of empirical design discussed later in this paper.
*The data set is available from http://landregistry.data.gov.uk/app/hpi. The 32 boroughs are: Barking, Barnet, Bexley, Brent, Bromley, Camden, Croydon, Ealing, Enfield, Greenwich, Hackney, Hammersmith & Fulham, Haringey, Harrow, Havering, Hillingdon, Hounslow, Islington, Kensington and Chelsea, Kingston upon Thames, Lambeth, Lewisham, Merton, Newham, Redbridge, Richmond upon Thames, Southwark, Sutton, Tower Hamlets, Waltham Forest, Wandsworth, City of Westminster. The aggregate series is denoted simply as London.
†Abbott and DeVita (2012) include the City of London in their analysis. While this is a local authority district within the Greater London, it is a very different in nature to the boroughs of London. In addition, data for the City of London are not available for the preferred frequency considered herein.
‡The CPI series was obtained from the Office of National Statistics (https://www.ons.gov.uk/)
Denoting the natural logarithms of the house price series as pt, house price returns are calculated as their difference rt=Δpt. § The use of changes in house prices to measure returns to housing is an issue that warrants some discussion.¶ This issue can be illustrated via consideration of the work of Bayer et al. (2010) where the return to housing is given as a combination of house price changes plus rental income. However, while this has a clear justification, the literature is dominated by studies measuring returns as house price changes without the inclusion of rental income. Examples of studies adopting this approach include the works of Dolde and Tirtiroglu (2002), Miller and Peng (2006), Morley and Thomas(2011, 2016). In light of the prevalence of the use of house price changes as a measure of returns, this approach will be adopted in the present study to allow consideration of the returns to purely holding housing as an asset or, alternatively expressed, the returns to owner occupation.‖
§Examination of the order of integration of the returns series (both nominal and real) using the Im et al. (2001) panel unit root test resulted in rejection of the null. Hence the returns series are all treated as stationary processes. Further details are available from the authors upon request.
¶We are grateful to the editor and an anonymous referee for raising the issue of measuring returns.
‖As noted, the measurement of returns has been extended by Bayer et al. (2010) to include rental income. Interestingly while this has a positive impact upon the level of returns, factors such as renovation costs and mortgage payments which have a negative impact are not considered.
The use of house price data for London in both disaggregated and aggregate form and in both nominal and real terms reflects clear decisions in the design of the empirical analysis undertaken in the current analysis. These variable-related assumptions or decisions are denoted here as Vi. Similarly, options available concerning decisions on the sample employed can be denoted as Si. Within the present analysis, the full or maximum sample available is considered as a starting point for the empirical analysis. However, to explore the sample dependence of inferences drawn, rolling samples are considered also. To include a relatively large number of observations in each of the rolling samples examined, the 251 observations of the full effective sample are employed to create an additional 72 samples containing 180 observations.** Via the use of these rolling samples, robustness of results across alternative sampling periods is explored.
**The full sample from January 1995 to December 2015 contains 252 observations. Following creation of a first difference to generate returns, this is reduced to 251. The 72 rolling samples of 180 observations are then given as Feb 1995 to Jan 2010, Mar 1995 to Feb 2010 through to Jan 2001 to Dec 2015.
3.2. Alternative modelling techniques
The prediction of a positive relationship between the returns on an asset and its associated risk is a standard feature of financial theory. However, as noted by Han (2013), a negative relationship between risk and returns has been noted repeatedly in the housing market literature (Dolde and Tirtiroglu, 1997;
Morley and Thomas, 2011; Lin and Fuerst, 2014). When considering the examination of risk-return relationships, an obvious and typically employed model to utilise is the GARCH-M specification (Engle et al., 1987). With returns on house prices denoted as rt, a standard GARCH(1, 1)-M model can be expressed as follows:
|
rt=μ+δσt+utut∼(0,σ2t)
|
(1)
|
|
σ2t=ϕ0+ϕ1u2t−1+ϕ2σ2t−1
|
(2)
|
Application of (1)-(2) allows examination of the risk-return relationship via the coefficient δ attached to the conditional standard deviation term (σt) in the mean equation. Although this specification is commonly applied in the literature, as has been noted by Scruggs (1998), variations on this model can be considered in terms of the specification of both the mean and variance equations. With regard to the variance equation, an obvious alternative to consider is the exponential GARCH (EGARCH) model of Nelson (1991). In addition to allowing a broader coverage of behaviour to capture potential asymmetric responses, the EGARCH model is attractive to practitioners as it does not require consideration of non-negativity constraints associated with the {ϕ1,ϕ2} parameters in the GARCH model of (2) above. The benefits of the EGARCH specification are apparent in its widespread adoption in the literature with Miller and Peng (2006), Lee (2009), Miles (2011), Morley and Thomas(2011, 2016) and Lin and Fuerst (2014) all employing this model. Extension of the GARCH-M model of (1)-(2) to consider an analogous EGARCH(1, 1)-M specification results in the model below:
|
rt=μ+δσt+utut∼(0,σ2t)
|
(3)
|
|
log(σ2t)=γ0+γ1log(σ2t−1)+γ2|ut−1σt−1|+γ3(ut−1σt−1)
|
(4)
|
To allow for the heavy, or thick, tails observed in financial series, the above models are estimated using the generalised error distribution (GED) for the error ut. In addition to allowing for heavy-tailed errors, use of the GED affords flexibility in the analysis conducted via unrestricted estimation of its underlying shape parameter (ν) for every model considered. Hence the degree of thickness of the tails of the error distribution can be tailored to the series, with movement from the Normal distribution (ν=2) to heavier tailed processes (ν<2) arising due to the estimation of smaller values for the shape parameter. Following the above discussion, the options available for these model-related components of the empirical design are denoted as Mi.
3.3. Dynamic specification
With regard to the specification of the mean equations in (1) and (3), these static expressions can be expanded to include a dynamic structure as noted by Scruggs (1998). Inclusion of an autoregressive component results in the GARCH(1, 1)-M specification of (5)-(6):
|
rt=μ+δσt+p∑i=1λirt−i+utut∼(0,σ2t)
|
(5)
|
|
σ2t=ϕ0+ϕ1u2t−1+ϕ2σ2t−1
|
(6)
|
and the EGARCH(1, 1)-M model of (7)-(8):
|
rt=μ+δσt+p∑i=1λirt−i+utut∼(0,σ2t)
|
(7)
|
|
log(σ2t)=γ0+γ1log(σ2t−1)+γ2|ut−1σt−1|+γ3(ut−1σt−1)
|
(8)
|
Estimated risk-return coefficients (ˆδ) can then be drawn from models employing alternative lag structures, or values of p. Investigators could consider the risk-return coefficients obtained from the static models discussed above (ˆδ0) or the maximum and minimum values (ˆδmax,ˆδmin) observed to be statistically significant across a range of values of p. Alternatively, a more typical approach is to consider coefficients obtained from models employing an optimised value of p, with the Akaike Information Criterion (AIC) frequently utilised as the means of selecting the optimum lag length. These coefficients are denoted herein as ˆδAIC with the optimum lag length defined as that generating the minimum value of the AIC, with the AIC specified as:
where ℓ and T denote the log-likelihood and sample size respectively. In light of the monthly frequency of the data considered in the present analysis, lags from a maximum value of p=12 down to a minimum of no lags (p=0) are considered herein. Continuing the above notation, these options or alternative possibilities concerning dynamic specification can be denoted as Di.
3.4. Empirical design components
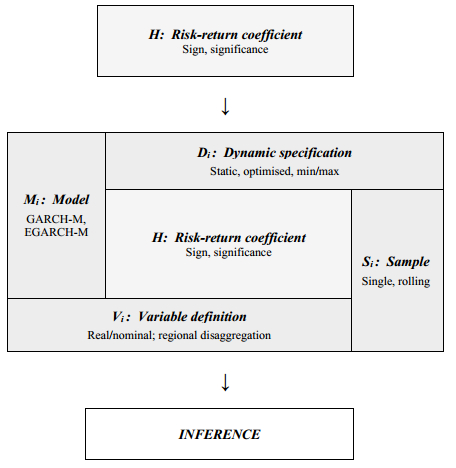
When considering the risk-return relationship via the use of (E)GARCH-M models, the parameter of interest is the risk coefficient in the relevant mean equation. The two issues of importance concerning this coefficient are its significance so as to determine whether a significant relationship exists and, if so, whether it is positive, as predicted by theory, or whether it is negative. However, as the above discussion in this section has made explicit, a series of decisions are required to structure the subsequent empirical analysis to permit testing of this hypothesis and inferences to be drawn. This movement from the initial focus upon the risk-return coefficient through to inference upon its nature is summarised in Figure One below. As this illustration depicts, the hypothesis of interest (H) providing the motivation for empirical analysis is surrounded by assumptions and decisions relating to variable selection and definition (Vi), sample selection (Si), the models employed (Mi) and dynamic specification (Di). It is argued that as a result of being embedded within these surrounding assumptions/options, any resulting inferences will be dependent upon not just the truth or falsity of the underlying hypothesis of interest, but also the impact of the decisions relating to {Vi,Si,Mi,Di}. Recognition of this 'jointness of testing' as a result of moving from an initial hypothesis to a composite testable form is present in the philosophy of science, particularly in relation to the Duhem-Quine thesis and the (im)plausibility of 'crucial experiments' allowing the evaluation of hypothesis of interest in isolation from surrounding factors.†† This issue has been considered in the economics literature also where Cross (1982) provides a theoretical analysis and discussion of the auxiliary assumptions associated with the empirical examination of monetarism. In the present study this form of analysis is extended to provide an empirical evaluation of the impact of variation in empirical design in relation to a very topical issue. As a result of this detailed consideration, the robustness of risk-return inferences is explored rather than consider a specific, single analysis.
††See Harding (1976) for a very readable collection of essays concerning the Duhem-Quine thesis.
4. Results
The results obtained from estimation of the GARCH(1, 1)-M and EGARCH(1, 1)-M models over the full sample are presented in Tables One and Two. As a result of the use of two models, alternative options for Mi are considered. Similarly, the use of both nominal and real returns for 33 regions (32 boroughs plus the aggregate London series) provides results for alternative Vi. Further to this, the tabulated results present a variety of risk-return coefficients obtained from alternative approaches to dynamic specification (Di). In particular, statistically significant (at the 5% level) estimated risk-return coefficients from static models (ˆδ0), obtained from AIC optimisation of the lag length (ˆδAIC) and the maximum and minimum values obtained across alternative lag specifications (ˆδmax,ˆδmin) are provided to evaluate the impact of variations in Di. While Tables One and Two allow examination of the impact of variation in {Vi,Mi,Di}, the results are generated using the full sample available and hence reflect use of a single value for Si. In recognition of this, further results are presented in Tables Three and Four where rolling samples are employed to consider the impact of variations in Si. These full sample and rolling sample results are considered in turn below.
Table 1. Risk-return coefficients: Nominal returns.
|
GARCH(1, 1)-M |
EGARCH(1, 1)-M |
| Borough |
ˆδ0 |
ˆδAIC |
ˆδmax |
ˆδmin |
ˆδ0 |
ˆδAIC |
ˆδmax |
ˆδmin |
| Barking |
−0.33 |
0.15 |
− |
− |
−3.03a |
0.18 |
−1.24 |
−3.03 |
| Barnet |
−0.56b |
0.67 |
−0.56 |
−0.56 |
−3.88a |
−21.21 |
−3.88 |
−11.89 |
| Bexley |
−0.23 |
−0.77 |
− |
− |
−3.45a |
−4.46b |
−1.41 |
−4.46 |
| Brent |
−0.30 |
0.11 |
− |
− |
4.62a |
0.10 |
7.59 |
−9.43 |
| Bromley |
−0.08 |
0.52 |
− |
− |
−4.08a |
0.22 |
49.62 |
−31.17 |
| Camden |
−0.11 |
−0.49 |
− |
− |
−3.58a |
−0.36 |
−3.58 |
−5.57 |
| Croydon |
0.03 |
0.22 |
− |
− |
−4.83a |
0.62 |
−2.06 |
−5.22 |
| Ealing |
−0.77b |
0.20 |
−0.77 |
−0.77 |
−3.46a |
−0.10 |
3.87 |
−3.46 |
| Enfield |
−0.02 |
0.40 |
− |
− |
−3.05a |
25.40 |
−0.96 |
−3.05 |
| Greenwich |
−0.57 |
−0.93 |
− |
− |
−3.19a |
−0.10 |
−3.19 |
−3.19 |
| Hackney |
−0.49 |
−0.16 |
− |
− |
−3.30a |
−0.98 |
−3.30 |
−44.60 |
| Hm & Ful |
−0.23 |
8.58 |
− |
− |
−3.51a |
1.74a |
24.50 |
−3.51 |
| Haringey |
−0.72b |
−0.39 |
−0.72 |
−0.72 |
−2.74a |
4.88a |
4.88 |
−2.81 |
| Harrow |
−0.10 |
−0.22 |
− |
− |
−2.99a |
−0.20 |
0.64 |
−4.23 |
| Havering |
−0.14 |
8.29 |
− |
− |
−3.07a |
1.10b |
11.40 |
−6.05 |
| Hillingdon |
−0.62b |
−0.60 |
−0.62 |
−0.62 |
−2.62a |
−1.00 |
0.50 |
−10.05 |
| Hounslow |
−0.15 |
−0.54 |
− |
− |
−2.53a |
−17.83b |
3.08 |
−24.57 |
| Islington |
−0.06 |
0.35 |
− |
− |
3.76a |
−8.76a |
3.76 |
−12.92 |
| Kensington |
−0.78b |
−0.53 |
−0.78 |
−0.78 |
−2.72a |
−0.53 |
−0.78 |
−2.72 |
| Kingston |
−0.16 |
0.02 |
− |
− |
−0.06 |
0.23 |
− |
− |
| Lambeth |
−0.18 |
0.51 |
3.76 |
3.76 |
4.59a |
0.45 |
4.59 |
0.96 |
| Lewisham |
0.19 |
−0.37 |
−1.67 |
−1.67 |
−3.21a |
−4.31 |
−1.86 |
−22.43 |
| Merton |
−1.10a |
−1.12 |
−1.10 |
−1.10 |
−3.25a |
−1.54 |
−0.76 |
−11.28 |
| Newham |
0.00 |
−0.04 |
− |
− |
−0.03 |
−11.98a |
−5.05 |
−27.98 |
| Redbridge |
−0.20 |
−0.35 |
− |
− |
−2.81a |
−11.43 |
−0.63 |
−2.81 |
| Richmond |
0.12 |
−0.21 |
− |
− |
−4.33a |
−0.09 |
−4.11 |
−4.33 |
| Southwark |
−0.45 |
0.19 |
3.21 |
3.21 |
−3.36a |
0.86a |
0.90 |
−3.36 |
| Sutton |
0.20 |
−0.11 |
− |
− |
−4.82a |
−0.23a |
41.25 |
−4.82 |
| Tower Ham |
−0.81a |
−1.14 |
−0.81 |
−0.81 |
−2.14a |
−1.46 |
−2.14 |
−9.73 |
| Walt For |
−0.08 |
−0.52 |
− |
− |
−4.37a |
−0.28 |
−4.37 |
−35.67 |
| Wandsworth |
−0.30 |
0.00 |
− |
− |
−6.02a |
−0.10 |
−1.11 |
−6.02 |
| Westminster |
−0.89a |
−0.89b |
−0.89 |
−0.95 |
−3.11a |
3.13 |
325.21 |
−17.90 |
| London |
−0.81a |
−0.36 |
−0.64 |
−0.81 |
−4.57a |
−0.26 |
−4.57 |
−9.02 |
| Notes: The above figures are the static mean equation, AIC optimised, maximum and minimum risk-return coefficients obtained from the GARCH-M and EGARCH-M specifications for nominal house returns. Significance at the 5% and 1% levels are denoted by a and b respectively. |
Table 2. Risk-return coefficients: Real returns.
|
GARCH(1, 1)-M |
EGARCH(1, 1)-M |
| Borough |
ˆδ0 |
ˆδAIC |
ˆδmax |
ˆδmin |
ˆδ0 |
ˆδAIC |
ˆδmax |
ˆδmin |
| Barking |
−0.48 |
0.21 |
− |
− |
−3.02a |
0.05 |
−1.07 |
−7.55 |
| Barnet |
−1.04a |
−166.15 |
−1.04 |
−1.04 |
−3.41a |
24.60a |
24.60 |
−4.39 |
| Bexley |
−3.30a |
0.49 |
−1.30 |
−3.30 |
−3.57a |
−6.92 |
−3.57 |
−4.46 |
| Brent |
−0.54 |
−0.09 |
− |
− |
−2.53a |
−22.20a |
−2.53 |
−22.20 |
| Bromley |
−0.39 |
−1.15 |
− |
− |
−4.08a |
58.69a |
58.69 |
−4.08 |
| Camden |
−0.16 |
0.28 |
− |
− |
−3.32a |
1.28 |
−3.32 |
−44.45 |
| Croydon |
−0.15 |
−0.97 |
− |
− |
−4.05a |
−22.60 |
13.78 |
−4.05 |
| Ealing |
−1.36a |
15.39 |
−0.99 |
−1.36 |
−3.32a |
6.86a |
6.86 |
−14.57 |
| Enfield |
−0.89a |
42.03 |
−0.89 |
−0.89 |
−2.83a |
−2.23a |
4.70 |
−2.83 |
| Greenwich |
−0.69 |
−1.37 |
−1.10 |
−1.10 |
−3.13a |
13.67a |
37.93 |
−32.41 |
| Hackney |
−0.42 |
−41.64 |
− |
− |
−3.83a |
−3.16a |
−3.16 |
−5.49 |
| Ham & Ful |
−0.35 |
−0.35 |
− |
− |
−3.22a |
4.01 |
−3.16 |
−25.01 |
| Haringey |
−0.73b |
−0.82 |
−0.73 |
−0.73 |
−2.84a |
16.89a |
16.89 |
−14.52 |
| Harrow |
−0.13 |
−0.02 |
− |
− |
−3.24a |
−0.94 |
−2.47 |
−4.60 |
| Havering |
−1.75a |
−1.04b |
−1.04 |
−1.75 |
−3.16a |
−6.34a |
2.35 |
−11.82 |
| Hillingdon |
−1.03a |
−0.09 |
−0.75 |
−1.03 |
−2.46a |
−18.81a |
66.56 |
−18.81 |
| Hounslow |
−0.11 |
0.03 |
−2.08 |
−2.08 |
3.27a |
−43.10a |
3.27 |
−43.10 |
| Islington |
0.00 |
−0.12 |
− |
− |
7.12a |
−23.43a |
7.12 |
−23.43 |
| Kensington |
−0.84 |
−0.22 |
− |
− |
−2.66a |
−0.42 |
−2.51 |
−7.19 |
| Kingston |
−0.30 |
−0.23 |
− |
− |
−3.59a |
0.54 |
2.99 |
−3.59 |
| Lambeth |
−0.36 |
0.85 |
− |
− |
−8.85a |
25.88 |
−8.85 |
−8.85 |
| Lewisham |
0.07 |
−0.57 |
−1.73 |
−1.73 |
0.13 |
39.25a |
58.49 |
−9.22 |
| Merton |
−1.18a |
−1.35 |
−1.18 |
−1.18 |
−3.28a |
−31.42a |
−3.28 |
−31.42 |
| Newham |
0.00 |
−0.01 |
− |
− |
−0.08 |
−0.02 |
−52.65 |
−52.65 |
| Redbridge |
−1.58a |
−0.29 |
−1.58 |
−1.58 |
−3.04a |
−0.32 |
−1.54 |
−9.27 |
| Richmond |
−0.43 |
−0.63 |
− |
− |
−3.92a |
−0.13 |
−2.82 |
−12.98 |
| Southwark |
−0.46 |
0.24 |
− |
− |
6.78a |
71.93a |
71.93 |
0.84 |
| Sutton |
−0.06 |
226.50 |
− |
− |
4.97a |
−16.62a |
18.34 |
−16.62 |
| Tower Ham |
−1.12a |
0.02 |
−1.12 |
−1.12 |
−2.38a |
−0.23 |
−2.38 |
−22.89 |
| Walt For |
−0.12 |
−0.06 |
− |
− |
−4.23a |
−0.01 |
−4.23 |
−6.71 |
| Wandsworth |
−0.46b |
0.25 |
−0.46 |
−0.46 |
−4.98a |
0.59a |
0.59 |
−4.98 |
| Westminster |
−0.85a |
−0.71 |
−0.59 |
−0.85 |
−2.37a |
−0.90 |
8.51 |
−3.81 |
| London |
−1.14a |
−0.61 |
−0.79 |
−1.14 |
−6.76a |
−0.15 |
−6.76 |
−6.76 |
| Notes: The above figures are the static mean equation, AIC optimised, maximum and minimum risk-return coefficients obtained from GARCH-M and EGARCH-M specifications for real house returns. Significance at the 5% and 1% levels are denoted by a and b respectively. |
Table 3. Rolling sample risk-return analysis: Nominal returns.
| Borough |
ˆδAIC |
CAIC |
CALL |
|
max |
min |
+ve |
−ve |
total |
+ve |
−ve |
| Barking |
0.65 |
−6.13 |
19 |
3 |
22 |
56 |
100 |
| Barnet |
10.14 |
−19.61 |
25 |
17 |
42 |
40 |
96 |
| Bexley |
0.56 |
−9.57 |
3 |
19 |
22 |
6 |
100 |
| Brent |
0.72 |
−1.12 |
14 |
1 |
15 |
44 |
99 |
| Bromley |
1.71 |
−32.01 |
58 |
11 |
69 |
90 |
79 |
| Camden |
−0.71 |
−1.33 |
0 |
22 |
22 |
1 |
100 |
| Croydon |
9.83 |
−6.16 |
13 |
14 |
26 |
42 |
82 |
| Ealing |
17.03 |
−6.81 |
40 |
3 |
43 |
79 |
97 |
| Enfield |
13.64 |
1.90 |
21 |
0 |
21 |
74 |
88 |
| Greenwich |
4.61 |
−40.68 |
14 |
14 |
28 |
43 |
100 |
| Hackney |
1.96 |
−6.05 |
47 |
4 |
51 |
60 |
100 |
| Ham & Ful |
26.10 |
−0.97 |
14 |
4 |
18 |
75 |
100 |
| Haringey |
53.86 |
0.49 |
26 |
0 |
26 |
78 |
99 |
| Harrow |
0.88 |
−7.70 |
31 |
6 |
36 |
83 |
100 |
| Havering |
15.57 |
−14.33 |
7 |
4 |
11 |
44 |
90 |
| Hillingdon |
0.98 |
−6.20 |
10 |
24 |
33 |
43 |
100 |
| Hounslow |
0.99 |
−8.71 |
3 |
18 |
21 |
21 |
100 |
| Islington |
6.54 |
−20.06 |
67 |
8 |
75 |
88 |
97 |
| Kensington |
− |
− |
0 |
0 |
0 |
3 |
96 |
| Kingston |
37.36 |
2.54 |
36 |
0 |
36 |
58 |
99 |
| Lambeth |
2.26 |
0.53 |
82 |
0 |
82 |
97 |
63 |
| Lewisham |
21.83 |
−62.64 |
6 |
92 |
97 |
39 |
100 |
| Merton |
−1.63 |
−18.57 |
0 |
51 |
51 |
28 |
100 |
| Newham |
0.79 |
−0.89 |
4 |
3 |
7 |
29 |
89 |
| Redbridge |
−4.51 |
−24.16 |
0 |
31 |
31 |
0 |
100 |
| Richmond |
−1.72 |
−6.20 |
0 |
17 |
17 |
0 |
100 |
| Southwark |
1.09 |
−11.18 |
13 |
1 |
14 |
25 |
92 |
| Sutton |
57.17 |
−84.19 |
19 |
17 |
36 |
54 |
100 |
| Tower Ham |
−1.72 |
−12.63 |
0 |
26 |
26 |
1 |
100 |
| Walt For |
−0.69 |
−41.02 |
0 |
33 |
33 |
38 |
82 |
| Wandsworth |
6.16 |
−0.40 |
6 |
1 |
7 |
17 |
99 |
| Westminster |
−1.44 |
−4.51 |
0 |
26 |
26 |
40 |
93 |
| London |
0.76 |
−7.49 |
1 |
4 |
6 |
1 |
99 |
| Notes: The first two columns of figures provide maximum and minimum values of the ˆδAIC significant at the 5% level over 72 rolling samples. CAIC is the percentage of samples generating significant ˆδAIC values with the percentage of negative and positive values along with the total percentage reported. CALL provides the percentage of samples generating significant ˆδ values with the percentages for both positive and negative coefficients provided. |
4.1. Full sample results
Turning to the results for the GARCH(1, 1)-M model in Tables One and Two, there is evidence of a significant, negative risk-return relationship for a number of series examined. More precisely, there are 9 (13) series for which the static model produces a significant coefficient for nominal (real) returns respectively. In contrast, results obtained from use of AIC optimisation depict a single significant risk-return coefficient for both the nominal and real series. Hence, alternative decisions on both Vi and Di influence the extent of the derivation of significant results. In terms of Vi, real returns produce a greater number of significant results than nominal returns, and (in)significance varies widely across regions. Similarly, the influence of decisions concerning Di is apparent via the difference in findings for coefficients from static and AIC optimised models. However, the extent of the detection of significant findings is relatively low given 33 series are examined, as is reflected in the small number of instances in which significant (at the 5% level) ˆδmax and ˆδmin coefficients are observed across the full set of lag lengths considered.
Considering the results for the EGARCH(1, 1)-M model, a vast increase in significant results for the static model is apparent with nominal and real returns producing 29 and 27 significant negative coefficients respectively. In addition, nominal and real returns generate 2 and 4 significant positive coefficients respectively for the static model. Consequently, variation in Mi via the movement from GARCH-M to EGARCH-M has a substantial impact upon the detection of significant risk-return relationships and leads also to the introduction of positive coefficient estimates to the analysis. Turning to the results for the AIC optimised coefficients, the nominal (real) series produce 4 (6) positive coefficients and 5 (9) negative coefficients. This represents a far more balanced outcome than that observed for the static model. The issue of the sign of the risk-return coefficient is more apparent when considering {ˆδmax,ˆδmin} for the EGARCH(1, 1)-M model where only one series fails to produce significant coefficients when considering nominal and real returns. Interestingly, these latter results show with regard to the sign of the risk-return coefficient, 31 (33) series produce negative coefficients for the nominal (real) series, while 14 (17) series produce positive coefficients. This range of outcomes for the EGARCH model compared to the GARCH specification, along with the variation in results observed under use of AIC optimisation and static models illustrates clearly the impact of Mi and Di upon inferences. While the use of nominal or real has an influence upon results derived, with a greater number of significant findings observed for the latter, the impact of Vi upon inferences is most apparent in terms of the effects of disaggregation, with widespread variation observed for the alternative series examined. In summary, these findings display a variation in sign and significance which indicates the counterintuitive negative risk-return relationship depicted by static EGARCH-M models is far less prevalent when alternative decisions are made concerning dynamic specification and modelling technique within the empirical design.
4.2. Rolling sample results
To explore the impact of the selected sample period upon inferences and whether the conclusions drawn from Tables One and Two are dependent upon the use of the specific full sample available, the EGARCH(1, 1)-M is estimated over 72 rolling samples of 180 observations. The results obtained from this analysis are presented in Tables Three and Four below. For each of the series considered, the maximum and minimum statistically significant values for the ˆδAIC across these 72 samples are reported. This provides information on the variation in, or range of, results arising from consideration of different samples. Further information on this variation is provided by CAIC which presents the percentage of samples for which statistically significant values of the ˆδAIC are observed (under the heading 'total') and their sign (under the headings 'positive' and 'negative'). To illustrate these results, consider the findings in Table Three for the first series (Barking). It can be seen that significant values of ˆδAIC from 0.65 down to −6.13 are observed across the 72 samples, and that while 19% of samples return significant positive ˆδAIC values and 3% return significant negative values, the ˆδAIC is insignificant for the remaining 78% of samples. As the ˆδAIC denotes the optimised value of ˆδ according to the AIC across 13 alternative lag lengths (p=0,1,...,12), further significant values of ˆδ are potentially available within each sample across the 12 other (non-optimal) lag lengths considered. In recognition of this, CALL is reported to provide information on the percentage of samples producing significant positive and negative values of ˆδ.
Considering the results in Tables Three and Four, 28 (31) regions produce negative values of ˆδAIC for nominal (real) returns, while 25 (30) regions produce positive values. These figures are clearly very similar in terms of the extent of negative/positive values. With regard to the percentages of samples for each series where the ˆδAIC was negative/positive, this is again balanced with an average of 14% (23%) of samples returning negative values and 18% (23%) producing positive values for nominal (real) returns. Therefore, the extension of the analysis to consider alternative sample periods has resulted in both increased detection of significant risk-return relationships using the AIC and evidence of its variability with a positive relationship being more frequent than a negative relationship. The results for CALL, where the percentage of significant values of δ are reported across all lag lengths considered over the 72 samples, show that nearly all samples return significant negative coefficients, with the percentages being 95% and 96% respectively for nominal and real returns. In contrast, on average less than half the samples return significant positive coefficients, with the average number of samples being 42% for both nominal and real returns. Therefore, while consideration of all available significant risk-return coefficient results in a prevalence of counterintuitive negative values, inspection of coefficients obtained from optimisation of the lag length leads to a relatively balanced finding in terms of negative and positive values.
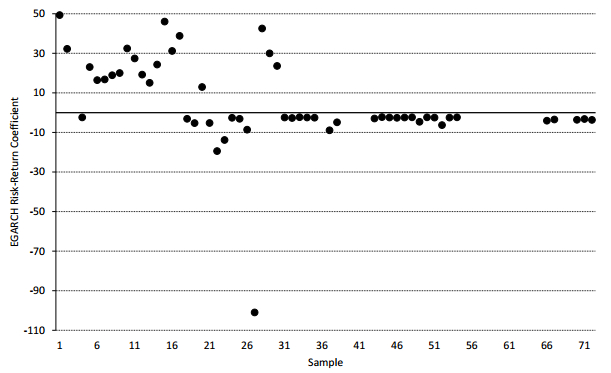
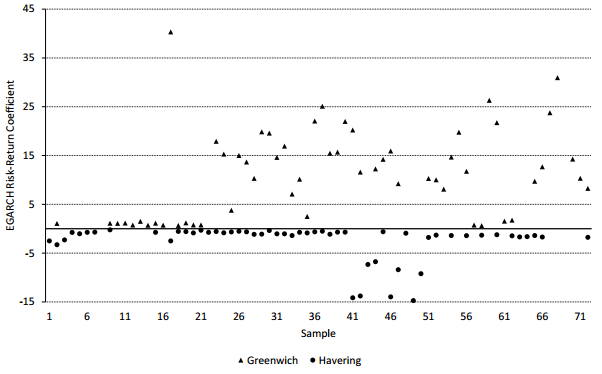
The above findings illustrate the variation in results concerning risk and return in the housing market due to alternative decisions regarding the use of models, variables, dynamic specification and samples. These findings have illustrated the empirical relevance of the jointness of hypothesis testing as depicted in Figure One. More specifically, the analysis has made explicit the dependence of the often cited counterintuitive finding of a negative risk-return relationship upon the approach taken to empirical design. While the full sample results for EGARCH-M model show the prevalence of negative coefficients, results observed for AIC optimisation and rolling samples do not support this finding. To illustrate further the variability of results across alternative samples and series (that is, alternative Si and Vi), Figures Two and Three present the significant ˆδAIC values for three London boroughs using the EGARCH(1, 1)-M model. In Figure Two, the values of the ˆδAIC for real house prices for Waltham Forest are plotted. To ease consideration of the crucial issue of the sign of the coefficient, a line at zero is included for the horizontal axis. From inspection of this graph, it can be seen that the first half of the 72 rolling samples are dominated by positive estimated coefficients while the second half of the samples does not return anything but negative values. As a consequence, variability in results is apparent when just the decision regarding samples is allowed to vary and decisions on the model, dynamic specification and variable are held constant. Such variation when just 1 factor is variable (and 3 are not), is compelling evidence against a certainty in the nature of the risk-return relationship. Similarly, to illustrate variability across alternative variables, Figure Three depicts analogous results for real house prices in Greenwich and Havering. In this instance, variation across series is illustrated as the former region generates positive ˆδAIC values only, while the latter has negative values only. In summary, Figures Two and Three present variability within series and across series respectively.
5. Concluding Remarks
The above analysis has provided a detailed examination of the risk-return relationship in the London housing market. In addition to providing the first findings within the literature for this issue, the analysis contains a more general message relating to the impact of decisions concerning empirical design upon risk-return inferences. The results provided indicate that while the counterintuitive negative risk-return relationship discussed frequently in the literature does arise, this is most prevalent when very specific decisions are taken with regard to models, dynamic specification and sample periods. In contrast to this, a more flexible and more preferred approach involving optimisation results in the generation of mixed results where a relatively balanced number of positive and negative findings are apparent. The analysis therefore provides a clear message concerning the impact of typically implicit and overlooked decisions on empirical design upon inferences. An obvious future line of research would involve a meta-analysis to consider the linkages between empirical design and inferences in previous research and hence a broader evaluation of the impact of design upon the robustness of conclusions relating to the risk-return relationship.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: