On the determination of first-mode stress intensity factors and T-stress in a continuous functionally graded beam using digital image correlation method

1.   Introduction

Multi-attribute decision making (MADM) is the mandatory circumstance for decision science. Its purpose is to differentiate probably the most specific alternative within feasible alternatives. The person making the decision needs to evaluate a given choice through various types of evaluation conditions, such as numbers, intervals, etc. However, it is difficult for one person in several circumstances since there are various uncertainties within the data, pick out the suitable one due to lack of expertise or infraction. Thus, to measure such risks and check the process, a wide family of theories was presented. First, Zadeh developed the concept of a fuzzy set (FS) ^[1] to solve those problems that contain uncertainty and ambiguity. In some cases, we must carefully consider membership as a non-membership value in the proper representation of objects that cannot be processed by FS. To overcome these difficulties, Atanassov proposed intuitionistic fuzzy sets (IFS) ^[2]. Many other theories had been developed, such as cubic IFS ^[3], interval-valued IFS ^[4], linguistic interval-valued IFS ^[5], etc. used by researchers. Recently, Alcantud et al. ^[6] presented the strategy to aggregate an infinite sequence of IFS; they also developed the scores and accuracy functions for temporal IFS and used the proposed functions for decision making. Thoroughly the theories mentioned above, substance are considered by experts, and the sum of their two memberships and non-membership values cannot exceed one.

Atanassov's intuitionistic fuzzy set only deals with insufficient data due to membership and non-membership values, but IFS cannot deal with incompatible and imprecise information. Molodtsov ^[7] proposed a general mathematical tool to deal with uncertain, ambiguous, and undefined substances, called soft sets (SS). Maji et al. ^[8] proposed the concept of a fuzzy soft set (FSS) by combining FS and SS. Ali et al. ^[9] presented different types of parameter reduction for bipolar FSS and established a novel decision-making methodology. Maji et al. proposed an intuitionistic fuzzy soft set (IFSS) with basic operations and properties ^[10]. Yang et al. ^[11] introduced the concept of interval-valued fuzzy soft sets (IVFSS) with operations and proved some important results by combining IVFS and SS, and they also used the developed concepts for decision-making. Akram et al. ^[12] proposed some novel hybrid structures, such as intuitionistic fuzzy n-soft sets, n-soft rough intuitionistic fuzzy sets as well as intuitionistic fuzzy n-soft rough sets and studied their desirable features. Additionally, they developed a decision-making method based on the developed structure to resolve the decision-making problem. Gerstenkorn and Mafiko ^[13] established a method for functionally measuring the interrelationship of IFS. Now, this method is called correlation and has developed characteristic coefficients.

Correlation plays an important role in statistics and engineering. The combined relationship of two variables can be used to estimate the interdependence of two variables through correlation analysis. Although probabilistic methods have been applied to various practical engineering problems, there are still some obstacles in probability strategies. For example, the probability of the process depends on the large amount of data collected, which is random. However, large complex systems have many vague uncertainties, so it is difficult to obtain accurate probability events. Therefore, due to limited quantitative information, results based on probability theory do not always provide useful information for experts. Also, in practical applications, sometimes there is not enough data to properly process standard statistical data. Due to the obstacles mentioned above, results based on probability theory are not always available to experts. Therefore, probabilistic methods are usually insufficient to resolve such inherent uncertainties in the data. Many researchers have proposed and suggested different methodologies to solve problems that contain uncertainty ^{[1,2,3,4,5,6]}. To measure the relationship between fuzzy numbers, Yu ^[14] established the correlation coefficient (CC) of fuzzy numbers. Chiang and Lin ^[15] discussed the fuzzy correlation of fuzzy data by implementing the subsequent strategies for conventional statistics; they gained the formula of fuzzy CC, which is enlightened in the fuzzy set.

Garg ^[16] developed an MCDM method based on weighted cosine similarity measures in an IFS environment and used the proposed technique for pattern identification and clinical diagnosis. Garg and Kumar ^[17] proposed some new similarity measures to measure the relative strength of IFS. They also compiled the number of connections for the set-pair analysis (SPA) and developed some new similarity and weighted similarity measures based on the specified SPA. Garg and Rani ^[18] extended the IFS technique to complex IFS (CIFS) and developed CC and WCC in the CIFS environment. Hung and Wu ^[19] proposed the center of gravity method to calculate the CC of IFS and extended the proposed method to IVIFS. Bustince and Burillo ^[20] introduced IVIFS and CC's correlation and proved the decomposition theorem about IVIFS. Hong ^[21] and Mitchell ^[22] also established CC for IFS and IVIFS, respectively. Garg and Arora introduced related metrics on IFSS and built the TOPSIS technique on the developed related measures ^[23]. Huang and Guo ^[24] established an improved CC based on IFS with their properties, and they also developed the IVIFS coefficient. Singh et al. ^[25] proposed one-parametric and two-parametric summaries of CC on IFS and applied the proposed technique to multi-attribute group decision-making problems.

Hwang and Yoon ^[26] developed the TOPSIS to solve decision-making problems. Using the TOPSIS method easily obtains the minimum distance from a positive ideal solution, which supports electing the finest alternative. After the TOPSIS method was invented, many researchers used the TOPSIS method for decision-making and extended this method to fuzzy and intuitionistic fuzzy environments ^{[27,28,29,30,31,32,33,34]}. Akram et al. ^[35] extended the TOPSIS technique to m-polar hesitant fuzzy TOPSIS for multi-criteria group decision making (MCGDM). Garg and Arora ^[36] developed a generalized version of the intuitionistic Fuzzy soft set (IFSS) with weighted average and geometric aggregation operators and constructed a decision-making technique to solve the problem in an intuitionistic fuzzy environment. Zhang et al. ^[37] established the TOPSIS-WAA method under covering based fuzzy rough set and based on MCDM; they designed a ranking structure in finite fuzzy covering approximation space (FCAS). Jiang et al. ^[38] described a unique method for grappling the MADM problem by mixing the developed model of rough set and the VIKOR method under the finite FCAS environment. They applied the developed method to choose the most appropriate drug for those who are victims of the ailment with Alzheimer's disease. The entropy measurement and the idea of the TOPSIS method based on CC were developed by using complex q-order neighbor pairs of fuzzy information and used well-established techniques for decision-making ^[39]. Many researchers have presented several models to deal with MCDM, MADM, and MCGDM problems, including PROMETHEE-EDAS methods ^[40], three-way decisions ^[41,42], CVPIFRS ^[43], and IF-TOPSIS ^[44] based on CIFRS models, etc.

Smarandache ^[45] extended the concept of soft sets to hypersoft sets (HSS) by replacing function F of one parameter with a multi-parameter (sub-attributes) function defined on the cartesian product of n different attributes. The established HSS is more flexible than soft sets and more suitable for decision-making environments. He also presented the further extension of HSS, such as crisp HSS, fuzzy HSS, intuitionistic fuzzy HSS, neutrosophic HSS, and plithogenic HSS. Nowadays, the HSS theory and its extensions rapidly progress, many researchers developed different operators and properties based on HSS and its extensions ^[46,47,48]. Abdel-Basset et al. ^[49] plithogenic set theory was used to eliminate uncertainty and evaluate the manufacturing industry's financial performance. Then, they used the VIKOR and TOPSIS methods to determine the weight of the financial ratio using the AHP method to achieve this goal. Abdel-Basset et al. ^[50] presented an effective combination of plithogenic aggregate operations and quality feature deployment procedures. The advantage of this combination is to improve accuracy, as a result, summarizes the decision-makers.

In this research, the TOPSIS technique is extended to IFHSS information, and the mechanism is based on IFHSNs assumptions. To measure the degree of dependency on IFHSS, we proposed a new CC on IFHSS and studied some properties of the developed CC. To achieve the goal accurately, the given TOPSIS technique can be extended to solve the multi-attribute decision-making (MADM) problem. In this study, our main goal is to introduce a novel CC under the IFHSS information and develop the TOPSIS method of IFHSS based on the proposed CC. To solve MADM problems based on the extended TOPSIS approach, develop an algorithm, and check the validity of the proposed technique with a numerical illustration. The correlation measures are given that IFHSS has been considered for the pairs of IFHSSs, which will be used to compute the interrelation as well as the scope of dependence between the elements. Because the existing IFS and IFSS are special cases of IFHSS, the measures that have been formulated are more general than the current measures. CC retains the linear relationship between under-considered elements. To find the general closeness coefficient, the researchers used the basic TOPSIS method, similarity measure, and distance. Meanwhile, in our developed method, CC can be used to calculate the closeness coefficient.

The rest of this article is organized as follows. In Section 2, we remembered some basic definitions, such as SS, HSS, and IFHSS, which will be used to construct this article's structure. In Section 3, we proposed the correlation and informational energies of IFHSS and developed CC and WCC and their properties by using the correlation and informational energies. Section 4 introduces the intuitionistic fuzzy hypersoft weighted average (IFHSWA) and intuitionistic fuzzy hypersoft weighted geometric (IFHSWG) operators with their decision-making approach. An extended TOPSIS technique based on CC in the IFHSS environment is proposed, and an algorithm is developed based on the proposed TOPSIS method to solve the MADM problem, and a numerical description is given in Section 5. Furthermore, we use some existing techniques to present comparative studies between our proposed methods. Likewise, present the advantages, naivety, flexibility as well as effectiveness of the planned algorithms. We organized a brief discussion and a comparative analysis of the recommended approach and the existing techniques in Section 6.

2.   Preliminaries

In this section, we recollect some basic definitions that help build the structure of the following manuscript such as soft set, hypersoft set, fuzzy hypersoft set, and intuitionistic fuzzy hypersoft set.

Definition 2.1. ^[7] Let $\mathcal{U}$ be the universal set and $\mathcal{E}$ be the set of attributes concerning $\mathcal{U}$. Let $\mathcal{P}\left(\mathcal{U}\right)$ be the power set of $\mathcal{U}$ and $\mathcal{A}\subseteq \mathcal{E}$. A pair ($\mathcal{F}, \mathcal{A}$) is called a soft set over $\mathcal{U}$ and its mapping is given as

It is also defined as:

Definition 2.2. ^[8] $\mathcal{F}\left(\mathcal{U}\right)$ be a collection of all fuzzy subsets over $\mathcal{U}$ and $\mathcal{E}$ be a set of attributes. Let $\mathcal{A}$ $\subseteq$ $\mathcal{E}$, then a pair ($\mathcal{F}, \mathcal{A}$) is called FSS over $\mathcal{U}$, where $\mathcal{F}$ is a mapping such as $\mathcal{F}$: $\mathcal{A}$ $\to$ 𝘍$\left(\mathcal{U}\right)$.

Definition 2.3. ^[45] Let $\mathcal{U}$ be a universe of discourse and $\mathcal{P}$($\mathcal{U}$) be a power set of $\mathcal{U}$ and $k$ = {${k}_{1}$, ${k}_{2}$, ${k}_{3}$, ..., ${k}_{n}$}, (n ≥ 1) be a set of attributes and set ${K}_{i}$ a set of corresponding sub-attributes of ${k}_{i}$ respectively with ${K}_{i}$ ∩ ${K}_{j}$ = φ for 𝑛 ≥ 1 for each 𝑖, 𝑗 𝜖 {1, 2, 3 … 𝑛} and 𝑖 ≠ 𝑗. Assume ${K}_{1}$ × ${K}_{2}$ × ${K}_{3}$× … × ${K}_{n}$ = $\stackrel{⃛}{\mathcal{A}}$ = $\left\{{a}_{1h}\times {a}_{2k}\times \cdots \times {a}_{nl}\right\}$ be a collection of multi-attributes, where 1 $\le$ $h$ $\le$ $\alpha$, 1 $\le$ $k$ $\le$ $\beta$, and 1 $\le$ $l$ $\le$ $\gamma$, and $\alpha$, $\beta$, and $\gamma$ $\in$ ℕ. Then the pair ($\mathcal{F}$, ${K}_{1}$ × ${K}_{2}$ × ${K}_{3}$× … × ${K}_{n}$ = $\stackrel{⃛}{\mathcal{A}}$) is said to be HSS over $\mathcal{U}$ and its mapping is defined as

$\mathcal{F}$: ${K}_{1}$ × ${K}_{2}$ × ${K}_{3}$× … × ${K}_{n}$ = $\stackrel{⃛}{\mathcal{A}}$ $\to \mathcal{P}$($\mathcal{U}$).

It is also defined as

Definition 2.4. ^[45] Let $\mathcal{U}$ be a universe of discourse and $\mathcal{P}$($\mathcal{U}$) be a power set of $\mathcal{U}$ and $k$ = {${k}_{1}$, ${k}_{2}$, ${k}_{3}$, ..., ${k}_{n}$}, (n ≥ 1) be a set of attributes and set ${K}_{i}$ a set of corresponding sub-attributes of ${k}_{i}$ respectively with ${K}_{i}$ ∩ ${K}_{j}$ = φ for 𝑛 ≥ 1 for each 𝑖, 𝑗 𝜖 {1, 2, 3 … 𝑛} and 𝑖 ≠ 𝑗. Assume ${K}_{1}$ × ${K}_{2}$ × ${K}_{3}$× … × ${K}_{n}$ = $\stackrel{⃛}{\mathcal{A}}$ = $\left\{{a}_{1h}\times {a}_{2k}\times \cdots \times {a}_{nl}\right\}$ be a collection of sub-attributes, where 1 $\le$ $h$ $\le$ $\alpha$, 1 $\le$ $k$ $\le$ $\beta$, and 1 $\le$ $l$ $\le$ $\gamma$, and $\alpha$, $\beta$, and $\gamma$ $\in$ ℕ and ${\mathbb{F}}^{\mathcal{U}}$ be a collection of all fuzzy subsets over $\mathcal{U}$. Then the pair ($\mathcal{F}$, ${K}_{1}$ × ${K}_{2}$ × ${K}_{3}$× … × ${K}_{n}$ = $\stackrel{⃛}{\mathcal{A}}$) is said to be FHSS over $\mathcal{U}$ and its mapping is defined as

It is also defined as

Example 2.1. Consider the universe of discourse $\mathcal{U}$ = $\left\{{\delta }_{1}, {\delta }_{2}\right\}$ and 𝔏 = $\left\{{ \ell }_{1} = Teaching \ methdology, { \ell }_{2} = Subjects, { \ell }_{3} = Classes\right\}$ be a collection of attributes with following their corresponding sub-attribute values are given as teaching methodology = ${L}_{1}$ = $\left\{{a}_{11} = project \ base, {a}_{12} = class \ discussion\right\}$, Subjects = ${L}_{2}$ = $\{{a}_{21} = Mathematics, {a}_{22} = Computer \ Science, \mathit{a}_{23} = Statistics \}$, and Classes = $\mathit{L}_{3}$ = $\{ \mathit{a}_{31} = Masters, \mathit{a}_{32} = Doctorol \}$.

Let $\stackrel{⃛}{\mathcal{A}}$ = ${L}_{1}$ × ${L}_{2}$ × ${L}_{3}$ be a set of attributes

$\stackrel{⃛}{\mathcal{A}}$ = ${L}_{1}$ × ${L}_{2}$ × ${L}_{3}$ = $\left\{{a}_{11}, {a}_{12}\right\}$ $\times$ $\left\{{a}_{21}, {a}_{22}, {a}_{23}\right\}$ $\times$ $\left\{{a}_{31}, {a}_{32}\right\}$

= $\left\{\begin{array}{c}\left({a}_{11}, {a}_{21}, {a}_{31}\right), \left({a}_{11}, {a}_{21}, {a}_{32}\right), \left({a}_{11}, {a}_{22}, {a}_{31}\right), \left({a}_{11}, {a}_{22}, {a}_{32}\right), \left({a}_{11}, {a}_{23}, {a}_{31}\right), \left({a}_{11}, {a}_{23}, {a}_{32}\right), \\ \left({a}_{12}, {a}_{21}, {a}_{31}\right), \left({a}_{12}, {a}_{21}, {a}_{32}\right), \left({a}_{12}, {a}_{22}, {a}_{31}\right), \left({a}_{12}, {a}_{22}, {a}_{32}\right), \left({a}_{12}, {a}_{23}, {a}_{31}\right), \left({a}_{12}, {a}_{23}, {a}_{32}\right), \end{array}\right\}$

$\stackrel{⃛}{\mathcal{A}}$ = $\left\{{\stackrel{ˇ}{a}}_{1}, {\stackrel{ˇ}{a}}_{2}, {\stackrel{ˇ}{a}}_{3}, {\stackrel{ˇ}{a}}_{4}, {\stackrel{ˇ}{a}}_{5}, {\stackrel{ˇ}{a}}_{6}, {\stackrel{ˇ}{a}}_{7}, {\stackrel{ˇ}{a}}_{8}, {\stackrel{ˇ}{a}}_{9}, {\stackrel{ˇ}{a}}_{10}, {\stackrel{ˇ}{a}}_{11}, {\stackrel{ˇ}{a}}_{12}\right\}$

Then the FHSS over $\mathcal{U}$ is given as follows:

Definition 2.5. ^[45] Let $\mathcal{U}$ be a universe of discourse and $\mathcal{P}$($\mathcal{U}$) be a power set of $\mathcal{U}$ and $k$ = {${k}_{1}$, ${k}_{2}$, ${k}_{3}$, ..., ${k}_{n}$}, (n ≥ 1) be a set of attributes and set ${K}_{i}$ a set of corresponding sub-attributes of ${k}_{i}$ respectively with ${K}_{i}$ ∩ ${K}_{j}$ = φ for 𝑛 ≥ 1 for each 𝑖, 𝑗 𝜖 {1, 2, 3 … 𝑛} and 𝑖 ≠ 𝑗. Assume ${K}_{1}$ × ${K}_{2}$ × ${K}_{3}$× … × ${K}_{n}$ = $\stackrel{⃛}{\mathcal{A}}$ = $\left\{{a}_{1h}\times {a}_{2k}\times \cdots \times {a}_{nl}\right\}$ be a collection of sub-attributes, where 1 $\le$ $h$ $\le$ $\alpha$, 1 $\le$ $k$ $\le$ $\beta$, and 1 $\le$ $l$ $\le$ $\gamma$, and $\alpha$, $\beta$, and $\gamma$ $\in$ ℕ and $IF{S}^{\mathcal{U}}$ be a collection of all intuitionistic fuzzy subsets over $\mathcal{U}$. Then the pair ($\mathcal{F}$, ${K}_{1}$ × ${K}_{2}$ × ${K}_{3}$× … × ${K}_{n}$ = $\stackrel{⃛}{\mathcal{A}}$) is said to be IFHSS over $\mathcal{U},$ and its mapping is defined as

It is also defined as

Where ${\mathcal{F}}_{\stackrel{⃛}{\mathcal{A}}}\left(\stackrel{ˇ}{a}\right)$ = $\left\{〈\delta , {\sigma }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right), {\tau }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right)〉: \delta \in \mathcal{U}\right\}$, where ${\sigma }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right)$ and ${\tau }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right)$ represents the membership and non-membership values of the attributes such as ${\sigma }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right)$, ${\tau }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right)$ $\in \left[0, 1\right]$, and 0 $\le$ ${\sigma }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right)$ + ${\tau }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right)$ $\le$ 1.

Simply an intuitionistic fuzzy hypersoft number (IFHSN) can be expressed as $\mathcal{F}$ = $\left\{\left({\sigma }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right), \ {\tau }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right)\right)\right\}$, where 0 $\le {\sigma }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right)+{\tau }_{\mathcal{F}\left(\stackrel{ˇ}{a}\right)}\left(\delta \right)\le$ 1.

Example 2.2. Consider the universe of discourse $\mathcal{U}$ = $\left\{{\delta }_{1}, {\delta }_{2}\right\}$ and 𝔏 = $\left\{{ \ell }_{1} = Teaching \ methdology, { \ell }_{2} = Subjects, { \ell }_{3} = Classes\right\}$ be a collection of attributes with following their corresponding attribute values are given as teaching methodology = ${L}_{1}$ = $\{{a}_{11} = project \ base, \mathit{a}_{12} = class \ discussion \}$ Subjects = $\mathit{L}_{2}$ = $\{ \mathit{a}_{21} = Mathematics, \mathit{a}_{22} = Computer \ Science, \mathit{a}_{23} = Statistics \}$, and Classes = $\mathit{L}_{3}$ = $\{ \mathit{a}_{31} = Masters, \mathit{a}_{32} = Doctorol \}$.

Let $\stackrel{⃛}{\mathcal{A}}$ = ${L}_{1}$ × ${L}_{2}$ × ${L}_{3}$ be a set of attributes

$\stackrel{⃛}{\mathcal{A}}$ = ${L}_{1}$ × ${L}_{2}$ × ${L}_{3}$ = $\left\{{a}_{11}, {a}_{12}\right\}$ $\times$ $\left\{{a}_{21}, {a}_{22}, {a}_{23}\right\}$ $\times$ $\left\{{a}_{31}, {a}_{32}\right\}$

= $\left\{\begin{array}{c}\left({a}_{11}, {a}_{21}, {a}_{31}\right), \left({a}_{11}, {a}_{21}, {a}_{32}\right), \left({a}_{11}, {a}_{22}, {a}_{31}\right), \left({a}_{11}, {a}_{22}, {a}_{32}\right), \left({a}_{11}, {a}_{23}, {a}_{31}\right), \left({a}_{11}, {a}_{23}, {a}_{32}\right), \\ \left({a}_{12}, {a}_{21}, {a}_{31}\right), \left({a}_{12}, {a}_{21}, {a}_{32}\right), \left({a}_{12}, {a}_{22}, {a}_{31}\right), \left({a}_{12}, {a}_{22}, {a}_{32}\right), \left({a}_{12}, {a}_{23}, {a}_{31}\right), \left({a}_{12}, {a}_{23}, {a}_{32}\right), \end{array}\right\}$

$\stackrel{⃛}{\mathcal{A}}$ = $\left\{{\stackrel{ˇ}{a}}_{1}, {\stackrel{ˇ}{a}}_{2}, {\stackrel{ˇ}{a}}_{3}, {\stackrel{ˇ}{a}}_{4}, {\stackrel{ˇ}{a}}_{5}, {\stackrel{ˇ}{a}}_{6}, {\stackrel{ˇ}{a}}_{7}, {\stackrel{ˇ}{a}}_{8}, {\stackrel{ˇ}{a}}_{9}, {\stackrel{ˇ}{a}}_{10}, {\stackrel{ˇ}{a}}_{11}, {\stackrel{ˇ}{a}}_{12}\right\}$

Then the IFHSS over $\mathcal{U}$ is given as follows:

3.   Correlation coefficient for intuitionistic fuzzy hypersoft set

In this section, the concept of correlation coefficient and weighted correlation coefficient on IFHSS is proposed with some basic properties.

Definition 3.1. Let $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{ }\mathcal{U}\right\}$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{ }\mathcal{U}\right\}$ be two IFHSSs defined over a universe of discourse $\mathcal{U}$. Then, their intuitionistic informational energies of $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ can be described as follows:

Definition 3.2. Let $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{ }\mathcal{U}\right\}$ be two IFHSSs defined over a universe of discourse $\mathcal{U}$. Then, their correlation measure between $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ can be described as follows:

Proposition 3.1. Let $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ be two IFHSSs and ${\mathcal{C}}_{IF\mathit{H}SS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ be a correlation between them, then the following properties hold.

1) ${\mathcal{C}}_{IF\boldsymbol{H}SS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\left)\right)$ = ${\mathrm{Ϛ}}_{IFHSS}(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$

2) ${\mathcal{C}}_{IFHSS}(\left(\mathcal{G}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ = ${\mathrm{Ϛ}}_{IFHSS}(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$

Proof. The proof is trivial.

Definition 3.3. Let $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{ }\mathcal{U}\right\}$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{ }\mathcal{U}\right\}$ be two IFHSSs, then correlation coefficient between them given as ${\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ and expressed as follows:

${\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ =

Proposition 3.2. Let $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ be two IFHSSs, then CC between them satisfies the following properties

1) 0 $\le$ ${\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ $\le$ 1

2) ${\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ = ${\delta }_{IFHSS}(\left(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\right), \left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right))$

3) If $\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right)$ = $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$, that is $\forall$ $i$, $k$, ${\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right) = {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)$, and ${\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right) = {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)$, then ${\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ = 1.

Proof 1. ${\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ $\ge$ 0 is trivial, here we only need to prove that ${\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ $\le$ 1.

From Eq 3.3, we have

By using Cauchy-Schwarz inequality

Therefore, ${{\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \ \stackrel{⃛}{\mathfrak{B}}\left)\right)}^{2}$ $\le {\mathrm{Ϛ}}_{IFHSS}(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})\times {\mathrm{Ϛ}}_{IFHSS}(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$. Hence, by using Definition 3.4, we have

${\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ $\le$ 1. So, 0 $\le$ ${\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ $\le$ 1.

Proof 2. The proof is obvious.

Proof 3. From Eq 3.5, we have

As we know that

${\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right) = {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)$, and ${\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right) = {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)$ $\forall$ $i$, $k$. We get

${\delta }_{IFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ = 1

Thus, prove the required result.

Definition 3.4. Let $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{ }\mathcal{U}\right\}$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{ }\mathcal{U}\right\}$ be two IFHSSs. Then, their correlation coefficient is given as ${\delta }_{IFHSS}^{1}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ and defined as follows:

Proposition 3.3. Let $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{ }\mathcal{U}\right\}$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ be two IFHSSs. Then, CC between them satisfies the following properties

1) 0 $\le$ ${\delta }_{IFHSS}^{1}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ $\le$ 1

2) ${\delta }_{IFHSS}^{1}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ = ${\delta }_{IFHSS}^{1}(\left(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\right), \left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right))$

3) If $\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right)$ = $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$, that is $\forall$ $i$, $k$, ${\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right) = {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)$, and ${\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right) = {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)$, then ${\delta }_{IFHSS}^{1}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ $=$ 1.

Proof. Similar to Proposition 3.2.

In this era, it is very necessary to consider the weights of IFHSS in practical applications. Whenever the decision-maker adjusts different weights for each alternative in the universe of discourse, the decision may be different. Consequently, it's particularly significant to plan the weight before decision making. Let $\Omega$ = ${\left\{{\Omega }_{1}, \ {\Omega }_{2}, \ {\Omega }_{3}, \dots , \ {\Omega }_{m}\right\}}^{T}$ be a weight vector for experts such as ${\Omega }_{k}$ $>$ 0, $\sum _{k = 1}^{m}{\Omega }_{k}$ = 1 and γ = ${\left\{{\mathrm{\gamma }}_{1}, \ {\mathrm{\gamma }}_{2}, \ {\mathrm{\gamma }}_{3}, \dots , \ {\mathrm{\gamma }}_{n}\right\}}^{T}$ be a weight vector for parameters such as ${\mathrm{\gamma }}_{i}$ $>$ 0, $\sum _{i = 1}^{n}{\mathrm{\gamma }}_{i}$ = 1. In the following, we develop the WCC between IFHSS by extending Definitions 3.3, 3.4.

Definition 3.5. Let $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ be two IFHSSs. Then, their weighted correlation coefficient is given as ${\delta }_{WIFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ and defined as follows:

Definition 3.6. Let $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ be two IFHSSs. Then, their weighted correlation coefficient is given as ${\delta }_{WIFHSS}^{1}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ and defined as follows:

If we consider $\Omega$ = {$\frac{1}{m}$, $\frac{1}{m}$, …, $\frac{1}{m}$} and $\mathrm{\gamma }$ = {$\frac{1}{n}$, $\frac{1}{n}$, …, $\frac{1}{n}$}, then ${\delta }_{WIFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ and ${\delta }_{WIFHSS}^{1}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ are reduced to ${\delta }_{WIFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ and ${\delta }_{WIFHSS}^{1}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ respectively.

Proposition 3.4. Let $(\mathcal{F}, \stackrel{⃛}{\mathcal{A}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ and $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$ = $\left\{\left({\delta }_{i}, {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right), {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)\right) ⎸{\delta }_{i}\in \mathcal{U}\right\}$ be two IFHSSs. Then, CC between them satisfies the following properties

1) 0 $\le$ ${\delta }_{WIFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ $\le$ 1

2) ${\delta }_{WIFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ = ${\delta }_{WIFHSS}(\left(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\right), \left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right))$

3) If $\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right)$ = $(\mathcal{G}, \stackrel{⃛}{\mathfrak{B}})$, that is $\forall$ $i$, $k$, ${\sigma }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right) = {\sigma }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)$, and ${\tau }_{\mathcal{F}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right) = {\tau }_{\mathcal{G}\left({\stackrel{ˇ}{a}}_{k}\right)}\left({\delta }_{i}\right)$, then ${\delta }_{WIFHSS}(\left(\mathcal{F}, \stackrel{⃛}{\mathcal{A}}\right), \ (\mathcal{G}, \stackrel{⃛}{\mathfrak{B}}\left)\right)$ $=$ 1.

Proof. Similar to Proposition 3.2.

4.   Aggregation operators for intuitionistic fuzzy hypersoft sets

In this section, intuitionistic fuzzy hypersoft weighted average and intuitionistic fuzzy hypersoft weighted geometric operators for IFHSSs are presented. We also develop the decision-making approach based on the proposed operators.

4.1.   Operational laws for IFHSNs

Definition 4.1.1. Let ${\mathfrak{J}}_{e}$ = $\left(\sigma , \ \tau \right)$, ${\mathfrak{J}}_{{e}_{11}}$ = $\left({\sigma }_{11}, \ {\tau }_{11}\right)$, and ${\mathfrak{J}}_{{e}_{12}}$ = $\left({\sigma }_{12}, \ {\tau }_{12}\right)$ be three IFHSNs and $\alpha$ be a positive real number, by algebraic norms, we have

1) ${\mathfrak{J}}_{{e}_{11}}\oplus$ ${\mathfrak{J}}_{{e}_{12}}$ = $\left\langle { {\sigma }_{11}+{\sigma }_{12}-{\sigma }_{11}{\sigma }_{12}, {\tau }_{11}{\tau }_{12} } \right\rangle$

2) ${\mathfrak{J}}_{{e}_{11}}\otimes {\mathfrak{J}}_{{e}_{12}}$ = $\left\langle { {\sigma }_{11}{\sigma }_{12}, {\tau }_{11}+{\tau }_{12}-{\tau }_{11}{\tau }_{12} } \right\rangle$

3) $\alpha {\mathfrak{J}}_{e}$ = $\left\langle { \left[1-{\left(1-\sigma \right)}^{\alpha }, {\left(\tau \right)}^{\alpha }\right] } \right\rangle$

4) ${\mathfrak{J}}_{e}^{\alpha }$ = $\left\langle { \left[{\left(\sigma \right)}^{\alpha }, 1-{\left(1-\tau \right)}^{\alpha }\right] } \right\rangle$

Some averaging and geometric aggregation operators for IFHSSs have been defined based on the above laws for the collection of IFHSNs $∆$.

Definition 4.1.2. Let ${\mathfrak{J}}_{{e}_{ij}}$ = $\left\langle { {\sigma }_{ij}, \ {\tau }_{ij} } \right\rangle$ be an IFHSN, ${\mathrm{\Omega }}_{i}$ and ${\mathrm{\gamma }}_{j}$ are weight vector for expert's and sub-attributes of selected parameters respectively with given conditions ${\mathrm{\Omega }}_{i}$ $>$ 0, $\sum _{i = 1}^{n}{\mathrm{\Omega }}_{i}$ = 1, ${\mathrm{\gamma }}_{j}$ $>$ 0, $\sum _{ j = 1}^{m}{\mathrm{\gamma }}_{j}$ = 1. Then IFHSWA operator is defined as

IFHSWA: ${∆}^{n}$ $\to$ $∆$ defined as follows

Theorem 4.1.1. Let ${\mathfrak{J}}_{{e}_{ij}}$ = $\left\langle { {\sigma }_{ij}, \ {\tau }_{ij} } \right\rangle$ be an IFHSNs, where $\left(i \ = \ 1, \ 2, \dots , \ n, and \ j = \ 1, \ 2, \dots , \ m\right)$, the aggregated value is also an IFHSN, such as

Proof. Similar to Theorem 3.1 ^[51].

Example 4.1.1. Let $\mathcal{U}$ = {${\delta }_{1}$, ${\delta }_{2}$, ${\delta }_{3}$, ${\delta }_{4}$} be a set of decision-makers with weights ${\mathrm{\Omega }}_{i}$ = ${\left(0.35, \ 0.25, \ 0.10, \ 0.30\right)}^{T}$, who are going to describe the qualities of a school under the defined set of attributes 𝔏 = $\left\{{e}_{1} = envoirnment, {e}_{2} = security\right\}$ and their corresponding sub-attributes ${e}_{1}$ = $\left\{{e}_{11} = \mathrm{g}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}\mathrm{r}\mathrm{y}, {e}_{12} = \mathrm{a} \ \mathrm{g}\mathrm{o}\mathrm{o}\mathrm{d} \ \mathrm{s}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m} \ \mathrm{o}\mathrm{f} \ \mathrm{c}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g}\right\}$, ${e}_{2}$ = $\left\{{e}_{21} = \mathrm{s}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y} \ \mathrm{g}\mathrm{u}\mathrm{a}\mathrm{r}\mathrm{d}\mathrm{s}, {e}_{22} = \mathrm{c}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{\text{'}}\mathrm{s}\right\}$. ${\mathfrak{L}}^{\text{'}}$ = ${e}_1$ × ${e}_2$ be a set of sub-attributes such as ${\mathfrak{L}}^{\text{'}}$ = ${e_1}$ × ${e_2}$ = $\{\mathit{e}_{11} , \mathit{e}_{12} \}$ $\times$ $\{ \mathit{e}_{21} , \mathit{e}_{22} \}$ = $\left\{\begin{array}{c}\left({e}_{11}, {e}_{21}\right), \left({e}_{11}, {e}_{22}\right), \left({e}_{12}, {e}_{21}\right), \left({e}_{12}, {e}_{22}\right)\end{array}\right\}$, ${\mathfrak{L}}^{\text{'}}$ = $\left\{{\stackrel{ˇ}{a}}_{1}, {\stackrel{ˇ}{a}}_{2}, {\stackrel{ˇ}{a}}_{3}, {\stackrel{ˇ}{a}}_{4}\right\}$ be a set of all multi sub-attributes with weights ${\mathrm{\gamma }}_{j}$ = ${\left(0.3, 0.4, 0.1, 0.2\right)}^{T}$. The assumed rating values of the experts for each sub-attribute in the form of IFHSNs $\left(\mathfrak{J}, \mathfrak{ }{\mathfrak{L}}^{\text{'}}\right)$ = ${\left\langle { {\sigma }_{ij}, {\tau }_{ij} } \right\rangle }_{4\times 4}$ given as follows

By using Eq 4.2,

Definition 4.1.3. Let ${\mathfrak{J}}_{{e}_{ij}}$ = $\left\langle { {\sigma }_{ij}, \ {\tau }_{ij} } \right\rangle$ be an IFHSN, ${\mathrm{\Omega }}_{i}$ and ${\mathrm{\gamma }}_{j}$ are weight vector for expert's and sub-attributes of selected parameters respectively with given conditions ${\mathrm{\Omega }}_{i}$ $>$ 0, $\sum _{i = 1}^{n}{\mathrm{\Omega }}_{i}$ = 1, ${\mathrm{\gamma }}_{j}$ $>$ 0, $\sum _{ j = 1}^{m}{\mathrm{\gamma }}_{j}$ = 1, then IFHSWG operator is defined as

Theorem 4.1.2. By using the IFHSWG operator, the obtained value is also an IFHSN and given as follows

Proof. Similar to Theorem 3.2 ^[51].

Definition 4.1.4. Let ${\mathfrak{J}}_{{e}_{ij}}$ = $⟨{\sigma }_{ij}, \ {\tau }_{ij}⟩$ be an IFHSN. Then, the score function under the IFHSS environment is defined as follows:

Example 4.1.2. Reconsider Example 4.1.1.

By using Eq 4.4, we have

$IFHSWG\left({\mathfrak{J}}_{{e}_{11}}, {\mathfrak{J}}_{{e}_{12}}, \dots , {\mathfrak{J}}_{{e}_{44}}\right)$ = $⟨.3567, .4002⟩$

4.2.   Decision-making approach based on proposed operators

An MADM approach is presented here based on the proposed operators and described the numerical examples for showing their efficiency.

4.2.1.   Proposed approach

Consider $\mathrm{\aleph }$ = $\left\{{\mathrm{\aleph }}^{1}, \ {\mathrm{\aleph }}^{2}, \ {\mathrm{\aleph }}^{3}, \dots , \ {\mathrm{\aleph }}^{s}\right\}$ and $\mathcal{U}$ = $\left\{{\delta }_{1}, \ {\delta }_{2}, \ {\delta }_{3}, \dots , \ {\delta }_{n}\right\}$ are set of $s$ alternatives $n$ experts respectively, the weights of experts is given as $\mathrm{\Omega }$ = ${\left({\mathrm{\Omega }}_{1}, \ {\mathrm{\Omega }}_{1}, \dots , \ {\mathrm{\Omega }}_{n}\right)}^{T}$ and ${\mathrm{\Omega }}_{i}>$0, $\sum _{i = 1}^{n}{\mathrm{\Omega }}_{i}$ = 1. Let $\mathfrak{L}$ = $\left\{{a}_{1}, \ {a}_{2}, \dots , \ {a}_{m}\right\}$ be a set of attributes and ${\mathfrak{L}}^{\text{'}}$ = $\left\{\left({a}_{1\rho }\times {a}_{2\rho }\times \dots \times {a}_{m\rho }\right) \mathrm{f}\mathrm{o}\mathrm{r} \ \mathrm{a}\mathrm{l}\mathrm{l} \rho \in \left\{1, 2, \dots , t\right\} \right\}$ be a collection of their corresponding sub-attributes, with weights γ = ${\left({\mathrm{\gamma }}_{1}, \ {\mathrm{\gamma }}_{2}, \ {\mathrm{\gamma }}_{3}, \dots , \ {\mathrm{\gamma }}_{\rho }\right)}^{T}$ such as ${\mathrm{\gamma }}_{\rho }$ $>$ 0, $\sum _{\rho = 1}^{t}{\mathrm{\gamma }}_{\rho }$ = 1. The elements in the collection of sub-attributes are multi-valued; for the sake of convenience, the elements of ${\mathfrak{L}}^{\text{'}}$ can be expressed as ${\mathfrak{L}}^{\text{'}}$ = $\left\{{\stackrel{ˇ}{a}}_{\partial }:\partial \in \left\{1, 2, \dots , k\right\}\right\}$. Experts give their preferences for each alternative in term of IFHSNs, such as ${\mathcal{L}}_{ij}^{\left(z\right)}$ = $\left({\sigma }_{ij}^{\left(z\right)}, \ {\tau }_{ij}^{\left(z\right)}\right)$, where 0 $\le$ ${\sigma }_{ij}^{\left(z\right)}, {\tau }_{ij}^{\left(z\right)}$ $\le$ 1 and ${\sigma }_{ij}^{\left(z\right)}+{\tau }_{ij}^{\left(z\right)}$ $\le$ 1 for all $i$, $j$ are given in Tables 1–4. Construct the aggregated IFHSNs ${∆}_{k}$, based on the expert's preference values for each alternative by using IFHSWG and IFHSWA operators. Finally, utilize the ranking of the alternatives based on the score function.

4.2.2.   Algorithm 1

Step 1. Develop the Intuitionistic fuzzy hypersoft matrix for each alternative.

Step 2. Aggregate the IFHSNs for each alternative into a collective decision matrix ${∆}_{k}$ by using the IFHSWA or IFHSWG operators.

Step 3. Compute the score values ${∆}_{k}$ for each alternative by using Eq 4.5.

Step 4. Choose the alternative with the maximum score value.

Step 5. Analyze the ranking.

5.   TOPSIS approach on IFHSS based on the correlation coefficient for solving DM problems

TOPSIS is one of the traditional approaches to deal with MADM complications. It is used to sort the priority order of feasible choices and use the most suitable choice by considering complete information. Using a collective assessment of a group of professionals, the results' overall credibility can be expanded in the decision-making process due to the increase in the sub-attribute of the given parameters. The TOPSIS technique under the IHFSS environment explains the uncertainty in real-world problems more effectively than the existing IFSs model. In this section, we will develop a mechanism for dealing with the complexities of decision-making by expanding the TOPSIS approach according to the rules of correlation coefficients under IFHSS Information. Hwang and Yoon ^[26] developed the TOPSIS approach and used it to encourage the evaluation of positive and negative ideal solutions to decision-making issues. Using the TOPSIS method, we can find the best alternatives with minimum and maximum PIS and NIS distances, respectively. TOPSIS technique proves that correlation measures are used to distinguish positive ideals from negative ideals by selecting rankings. In most cases, researchers use the TOPSIS method to discover closeness coefficients with different distance types and comparable measures. The TOPSIS technique with the correlation coefficient is more suitable for finding the closeness coefficient than distance and similarity measures. Because the correlation measure retains the linear relationship between the factors considered. By using the developed CC, an algorithm based on the TOPSIS method will be introduced to select the most suitable option.

5.1.   Algorithm 2. TOPSIS method based on CC for IFHSS to solve MADM problem

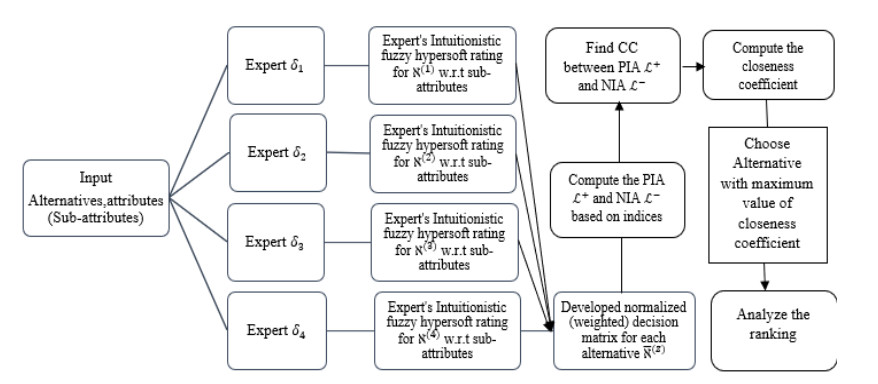
Assume a set of "$\mathrm{s}$" alternatives such as $\mathrm{\aleph }$ = $\left\{{\mathrm{\aleph }}^{1}, \ {\mathrm{\aleph }}^{2}, \ {\mathrm{\aleph }}^{3}, \dots , \ {\mathrm{\aleph }}^{\mathrm{s}}\right\}$ for assessment under the team of experts $\mathcal{U}$ = $\left\{{\mathrm{\delta }}_{1}, \ {\mathrm{\delta }}_{2}, \ {\mathrm{\delta }}_{3}, \dots , \ {\mathrm{\delta }}_{\mathrm{n}}\right\}$ with weights $\mathrm{\Omega }$ = ${\left({\mathrm{\Omega }}_{1}, \ {\mathrm{\Omega }}_{1}, \dots , \ {\mathrm{\Omega }}_{\mathrm{n}}\right)}^{\mathrm{T}}$ and ${\mathrm{\Omega }}_{\mathrm{i}}>$0, $\sum _{\mathrm{i} = 1}^{\mathrm{n}}{\mathrm{\Omega }}_{\mathrm{i}}$ = 1. Let $\mathfrak{L}$ = $\left\{{\mathrm{a}}_{1}, \ {\mathrm{a}}_{2}, \dots , \ {\mathrm{a}}_{\mathrm{m}}\right\}$ be a set of attributes and ${\mathfrak{L}}^{\mathrm{\text{'}}}$ = $\left\{\left({\mathrm{a}}_{1\mathrm{\rho }}\times {\mathrm{a}}_{2\mathrm{\rho }}\times \dots \times {\mathrm{a}}_{\mathrm{m}\mathrm{\rho }}\right) \ \mathrm{f}\mathrm{o}\mathrm{r} \ \mathrm{a}\mathrm{l}\mathrm{l} \ \mathrm{\rho }\in \left\{1, \ 2, \dots , \ \mathrm{t}\right\} \ \right\}$ be a collection of their corresponding sub-attributes, with weights γ = ${\left({\mathrm{\gamma }}_{1\mathrm{\rho }}, \ {\mathrm{\gamma }}_{2\mathrm{\rho }}, \ {\mathrm{\gamma }}_{3\mathrm{\rho }}, \dots , \ {\mathrm{\gamma }}_{\mathrm{m}\mathrm{\rho }}\right)}^{\mathrm{T}}$ such as ${\mathrm{\gamma }}_{\mathrm{\rho }}$ $>$ 0, $\sum _{\mathrm{\rho } = 1}^{\mathrm{t}}{\mathrm{\gamma }}_{\mathrm{\rho }}$ = 1. The elements in the collection of sub-attributes are multi-valued; for the sake of convenience, the elements of ${\mathfrak{L}}^{\mathrm{\text{'}}}$ can be expressed as ${\mathfrak{L}}^{\mathrm{\text{'}}}$ = $\left\{{\stackrel{ˇ}{\mathrm{a}}}_{\partial }:\partial \in \left\{1, \ 2, \ \dots , \mathrm{k}\right\}\right\}$. The team of experts {${\mathrm{\delta }}_{\mathrm{i}}$: $\mathrm{i}$ = 1, 2, …, $\mathrm{n}$} evaluate the alternatives {${\mathrm{\aleph }}^{\left(\mathrm{z}\right)}$: $\mathrm{z}$ = 1, 2, …, $\mathrm{s}$} under the considered sub-attributes {${\stackrel{ˇ}{\mathrm{a}}}_{\partial }$: $\partial$ = 1, 2, …, $\mathrm{k}$} given in the form of IFHSNs such as ${\mathcal{L}}_{\mathrm{i}\mathrm{j}}^{\left(\mathrm{z}\right)}$ = $\left({\rm{ \mathsf{ σ} }}_{\mathrm{i}\mathrm{j}}^{\left(\mathrm{z}\right)}, \ {\rm{ \mathsf{ τ} }}_{\mathrm{i}\mathrm{j}}^{\left(\mathrm{z}\right)}\right)$, where 0 $\le$ ${\rm{ \mathsf{ σ} }}_{\mathrm{i}\mathrm{j}}^{\left(\mathrm{z}\right)}, {\rm{ \mathsf{ τ} }}_{\mathrm{i}\mathrm{j}}^{\left(\mathrm{z}\right)}$ $\le$ 1 and ${\rm{ \mathsf{ σ} }}_{\mathrm{i}\mathrm{j}}^{\left(\mathrm{z}\right)}+{\rm{ \mathsf{ τ} }}_{\mathrm{i}\mathrm{j}}^{\left(\mathrm{z}\right)}$ $\le$ 1 for all $\mathrm{i}$, $\mathrm{j}$. A flowchart for the method is presented in Figure 1.

Step 1. Construct a matrix for each alternative {${\mathrm{\aleph }}^{\left(z\right)}$: $z$ = 1, 2, …, $s$} in the form of IFHSNs under-considered multi-valued sub-attributes such as follows:

Step 2. Construct the weighted decision matrix for each alternative ${\stackrel{-}{\mathrm{\aleph }}}^{\left(z\right)}$ = ${\left({\stackrel{-}{\mathcal{L}}}_{ij}^{\left(z\right)}\right)}_{n\times \partial }$, where

Here ${\mathrm{\Omega }}_{i}$ and ${\mathrm{\gamma }}_{j}$ are the weights for the ${i}^{th}$ expert and ${j}^{th}$ sub-attribute respectively.

Step 3. Find the indices ${ \hbar }_{ij}$ = arg ${max}_{z}\left\{{\theta }_{ij}^{\left(z\right)}\right\}$ and ${g}_{ij}$ = arg ${min}_{z}\left\{{\theta }_{ij}^{\left(z\right)}\right\}$ for each expert ${\delta }_{i}$ and sub-attribute ${\stackrel{ˇ}{a}}_{j}$ from CC matrices, and determine the PIA and NIA based on indices such as follows:

and

Step 4. Compute the CC between each alternative of weighted decision matrices ${\stackrel{-}{\mathrm{\aleph }}}^{\left(z\right)}$ and PIA ${\mathcal{L}}^{+}$ such as follows:

Step 5. Compute the CC between each alternative of weighted decision matrix ${\stackrel{-}{\mathrm{\aleph }}}^{\left(z\right)}$ and NIA ${\mathcal{L}}^{-}$ such as follows:

Step 6. The closeness coefficient for each alternative can be found as follows:

Where $\mathcal{K}\left({\stackrel{-}{\mathrm{\aleph }}}^{\left(z\right)}, {\mathcal{L}}^{-}\right)$ = 1 $-$ ${q}^{\left(z\right)}$ and $\mathcal{K}\left({\stackrel{-}{\mathrm{\aleph }}}^{\left(z\right)}, {\mathcal{L}}^{+}\right)$ = 1 $-$ ${p}^{\left(z\right)}$.

Step 7. Choose the alternative with a maximum value of closeness coefficient

Step 8. Analyze the ranking of the alternatives.

The graphical representation of the above-presented algorithm can be seen in Figure 1.

5.2.   Application of proposed TOPSIS technique and aggregation operators for decision making

A university requires the appointment of a teacher. After a preliminary review, there are still four candidates (alternatives) that need further evaluation, such as $\mathrm{\aleph }$ = $\left\{{\mathrm{\aleph }}^{1}, \ {\mathrm{\aleph }}^{2}, \ {\mathrm{\aleph }}^{3}, \ {\mathrm{\aleph }}^{4}\right\}$. The president of the university chooses a team of four experts $\mathcal{U}$ = $\left\{{\delta }_{1}, {\delta }_{2}, {\delta }_{3}, {\delta }_{4}\right\}$ having weights ${\left(0.2 0.3, 0.4, 0.1\right)}^{T}$ to evaluate the remaining alternatives. The team of experts decides the criteria (attributes) for the selection of teacher such as 𝔏 = $\{{ \ell }_{1} = \mathrm{P}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}, { \ell }_{2} = \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{s}, { \ell }_{3} = \mathrm{Q}\mathrm{u}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \}$ be a collection of attributes and their corresponding sub-attribute are given as Publications = ${ \ell }_{1}$ = $\left\{{a}_{11} = more \ than \ 10, {a}_{12} = less \ than \ 10\right\}$, Subjects = ${ \ell }_{2}$ = $\{{a}_{21} = Mathematics, \mathit{a}_{22} = Computer \ Science \}$, and Qualification = $\mathit{ \ell }_3$ = $\{ \mathit{a}_{31} = Masters, \mathit{a}_{32} = Doctorol \}$. Let ${\mathfrak{L}}^{\text{'}}$ = ${ \ell }_{1}$ × ${ \ell } _{2}$ × ${ \ell } _{3}$ be a set of sub-attributes

${\mathfrak{L}}^{\text{'}}$ = $\left\{{\stackrel{ˇ}{a}}_{1}, {\stackrel{ˇ}{a}}_{2}, {\stackrel{ˇ}{a}}_{3}, {\stackrel{ˇ}{a}}_{4}, {\stackrel{ˇ}{a}}_{5}, {\stackrel{ˇ}{a}}_{6}, {\stackrel{ˇ}{a}}_{7}, {\stackrel{ˇ}{a}}_{8}\right\}$ be a set of all multi sub-attributes with weights ${\left(0.12, 0.18, \mathrm{0.1, 0.15}, 0.05, 0.22, 0.08, 0.1\right)}^{T}$. Each expert will evaluate each alternative's ratings in the form of IFHSNs under the considered multi-valued sub-attributes. The developed method to find the best alternative is as follows.

Step 1. Develop the decision matrices for each alternative under defined multi sub-attributes according to each decision-maker's ratings in terms of IFHSNs.

Step 2. Construct the weighted decision matrix for each alternative ${\stackrel{-}{\mathrm{\aleph }}}^{\left(z\right)}$ = ${\left({\stackrel{-}{\mathcal{L}}}_{ij}^{\left(z\right)}\right)}_{n\times \partial }$ given in Tables 5–8, such as follows:

Step 3. Determine the PIA and NIA based on indices by using Eqs 5.2 and 5.3 such as follows:

Step 4. Compute the CC between ${\stackrel{-}{\bf{\aleph }}}^{\left(\bf{z}\right)}$ and PIA ${\mathcal{L}}^{+}$ by using Eq 5.4, given as ${p}^{\left(1\right)}$ = .99915, ${p}^{\left(2\right)}$ = .99811, ${p}^{\left(3\right)}$ = .99746, ${p}^{\left(4\right)}$ = .99787.

Step 5. Compute the CC between ${\stackrel{-}{\bf{\aleph }}}^{\left(\bf{z}\right)}$ and NIA ${\mathcal{L}}^{-}$ by using Eq 5.5, given as ${q}^{\left(1\right)}$ = .99742, ${q}^{\left(2\right)}$ = .99806, ${q}^{\left(3\right)}$ = .99870, ${q}^{\left(4\right)}$ = .99870.

Step 6. Compute the closeness coefficient by using Eq 5.6.

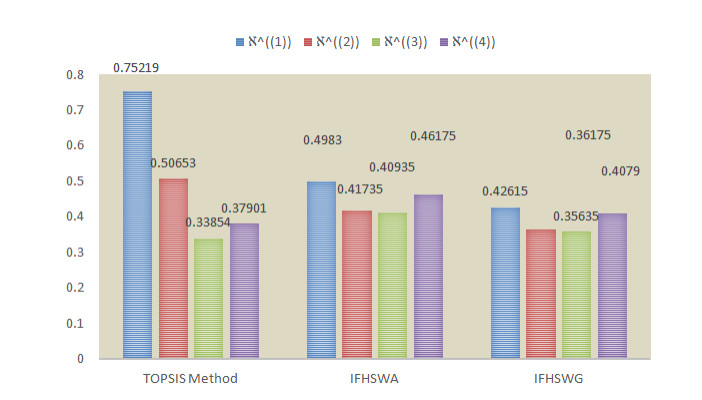
${\mathcal{R}}^{\left(1\right)}$ = .75219, ${\mathcal{R}}^{\left(2\right)}$ = .50653, ${\mathcal{R}}^{\left(3\right)}$ = .33854, and ${\mathcal{R}}^{\left(4\right)}$ = .37901.

Step 7. Choose the alternative with maximum closeness coefficient ${\mathcal{R}}^{\left(1\right)}$ = .75219, so ${\mathrm{\aleph }}^{\left(1\right)}$ be the best alternative.

Step 8. Analyze the ranking of the alternatives, we can see ${\mathcal{R}}^{\left(1\right)}$ $>$ ${\mathcal{R}}^{\left(2\right)}>{\mathcal{R}}^{\left(4\right)}$ $>$ ${\mathcal{R}}^{\left(3\right)}$, so the ranking of the alternatives is ${\mathrm{\aleph }}^{\left(1\right)}$ $>$ ${\mathrm{\aleph }}^{\left(2\right)}>{\mathrm{\aleph }}^{\left(4\right)}$ $>$ ${\mathrm{\aleph }}^{\left(3\right)}$.

Graphical representation of the ranking of the alternatives can be seen in Figure 2.

5.3.   Selection of best alternative by using proposed IFHSWA operator

Step 1. The experts will evaluate the condition in the case of IFHSNs; there are just four alternatives; sub-attributes and a summary of their scores given in Tables 1–4.

Step 2. Experts' opinions on each alternative are summarized by using Eq 4.2. Therefore, we get

${∆}_{1}$ = $⟨.4296, .5670⟩$, ${∆}_{2}$ = $⟨.4956, .3391⟩$, ${∆}_{3}$ = $⟨.3303, .4884⟩$, and ${∆}_{4}$ = $⟨.3547, .5695⟩$.

Step 3. Score values by using Equation 4.5 for each alternative.

$\mathbb{S}\left({∆}_{1}\right)$ = .4983, $\mathbb{S}\left({∆}_{2}\right)$ = .41735, $\mathbb{S}\left({∆}_{3}\right)$ = .40935, and $\mathbb{S}\left({∆}_{4}\right)$ = .46175.

Step 4. Therefore, the ranking of the alternatives is as follows $\mathbb{S}\left({∆}_{1}\right)$ $>$ $\mathbb{S}\left({∆}_{4}\right)$ $>$ $\mathbb{S}\left({∆}_{2}\right)$ $>$ $\mathbb{S}\left({∆}_{3}\right)$. So, ${\mathrm{\aleph }}^{\left(1\right)}$ $>$ ${\mathrm{\aleph }}^{\left(4\right)}>{\mathrm{\aleph }}^{\left(2\right)}$ $>$ ${\mathrm{\aleph }}^{\left(3\right)}$, hence, the alternative ${\mathrm{\aleph }}^{\left(1\right)}$ is the most suitable alternative.

5.4.   Selection of best alternative by using proposed IFHSWG operator

Step 1. The experts will evaluate the condition in the case of IFHSNs; there are just four alternatives; sub-attributes and a summary of their scores given in Tables 1–4.

Step 2. Experts' opinions on each alternative are summarized by using Eq 4.4. Therefore, we get

${∆}_{1}$ = $⟨.3144, .5379⟩$, ${∆}_{2}$ = $⟨.2815, .4420⟩$, ${∆}_{3}$ = $⟨.2904, .4223⟩$, and ${∆}_{4}$ = $⟨.2713, .5445⟩$.

Step 3. Score values by using Eq 4.5 for each alternative.

$\mathbb{S}\left({∆}_{1}\right)$ = .42615, $\mathbb{S}\left({∆}_{2}\right)$ = .36175, $\mathbb{S}\left({∆}_{3}\right)$ = .35635, and $\mathbb{S}\left({∆}_{4}\right)$ = .40790.

Step 4. Therefore, the ranking of the alternatives is as follows $\mathbb{S}\left({∆}_{1}\right)$ $>$ $\mathbb{S}\left({∆}_{4}\right)$ $>$ $\mathbb{S}\left({∆}_{2}\right)$ $>$ $\mathbb{S}\left({∆}_{3}\right)$. So, ${\mathrm{\aleph }}^{\left(1\right)}$ $>$ ${\mathrm{\aleph }}^{\left(4\right)}>{\mathrm{\aleph }}^{\left(2\right)}$ $>$ ${\mathrm{\aleph }}^{\left(3\right)}$, hence, the alternative ${\mathrm{\aleph }}^{\left(1\right)}$ is the most suitable alternative.

6.   Discussion and comparative analysis

In the following section, we will discuss the effectiveness, naivety, flexibility, and advantages of the proposed methods and algorithms. We also conducted a brief comparative analysis of the following: suggested methods and existing methods.

6.1.   Advantages and flexibility of proposed approach

The recommended techniques are practical and applicable to all forms of input data. Here we introduce two novel algorithms based on IHFSS; TOPSIS; the other is IFHSWA and IFHSWG. Both algorithms are practical and can provide the best results in MADM problems. The recommended algorithms are simple and easy to understand, can deepen the understanding, and apply to many types of choices and measures. Both algorithms are flexible and easy to change to suit different situations, input, and output. There are subtle differences between the suggested methods' rankings because different techniques have different ranking methods so that they can be affordable according to their considerations.

6.2.   Superiority of the proposed method

Through this research and comparative analysis, we have concluded that the proposed methods' results are more general than prevailing techniques. However, in the decision-making process, compared with the existing decision-making methods, it contains more information to deal with the data's uncertainty. Moreover, many of FS's mixed structure has become a special case of IFHSS, add some suitable conditions. In it, the information related to the object can be expressed more accurately and empirically, so it is a convenient tool for combining inaccurate and uncertain information in the decision-making process. Therefore, our proposed method is effective, flexible, simple, and superior to other hybrid structures of fuzzy sets.

6.3.   Comparative analysis

By using the technique of Zadeh ^[1], we deal with the true information of the alternatives, but this method cannot deal with falsity objects and multi sub-attributes of the alternatives. By utilizing the Xu et al. ^[52] and Zhang et al. ^[53] methodologies, we cannot deal with the alternatives' multi-sub-attribute information. But our proposed method can easily solve these obstacles and provide more effective results for the MADM problem. Instead of this, our developed method is an advanced technique that can handle alternatives with multi-sub-attributes information. A comparison can be seen in the above-listed Table 9. However, on the other hand, the methodology we have established deals with the truthiness and falsity of alternatives with multi sub-attributes. Therefore, the technique we developed is more efficient and can provide better results for decision-makers through a variety of information comparative to existing techniques.

7.   Conclusion

The investigated study utilizes the IFHSS to address the insufficient, ambiguous, and inconsistent data by considering membership degree and non-membership degree over the parameters' set. The novel concept of CC and WCC under the IFHSS environment with their properties are proposed in the present research. Based on the developed correlation measures, an extended TOPSIS method has been introduced by considering the set of attributes with their corresponding sub-attributes and the decision-makers. We also developed the correlation indices to find the PIA and NIA. To find the ranking of the alternatives, we define the closeness coefficient under the established TOPSIS method. Moreover, the IFHSWA and IFHSWG operators also defined and presented the decision-making techniques based on developed operators. Finally, a numerical illustration has been described to solve the MADM problem by using the proposed TOPSIS method and other developed techniques. Furthermore, A comparative analysis is presented to verify the validity and demonstration of the proposed method. Finally, based on the results obtained, it is concluded that the suggested techniques showed higher stability and practicality for decision-makers in the decision-making process. In the future, we plan to extend our work to (i) CC for multipolar Intuitionistic fuzzy hypersoft set, (ii) CC for the interval-valued intuitionistic fuzzy hypersoft set, and (iii) CC for the multipolar interval-valued intuitionistic fuzzy hypersoft set.

Acknowledgments

This research is partially supported by a grant from the National Natural Science Foundation of China (11971384).

Conflict of interest

The authors declare no conflict of interest.