1. Introduction

In recent years, particle assemblies, as exemplified in Figure 1, have gained increased attention due to the needs for new generation of materials with tailored physical and mechanical properties ^[1,2,3,4]. Opposing to the conventional materials, their deformation mechanisms can be tuned for specific purposes or they lead to the level of desired porosity for cell colonization and deliver biological signals via molecule adsorption or encapsulation ^[5,6,7,8].

Common assembly process follows positioning of randomly aligned particles to the desired configuration, which is known as optical trapping in the literature ^[6,10]. For moving particles and accomplishing the process, optical forces exerted by laser beams are preferred because of their precise manipulation without mechanical contact ^[9]. Pick and place methods, which are conventionally based on operator's decision and feedback, are used ^[1,11]. However, manual decision and feedback methods are usually cumbersome in consideration to time and lack of expertise ^[9]. Therefore, in the present article, an efficient automated path planning method is proposed and simulations related to the method are reported. The method uses optimal permutation based on particle paths and finds non-overlapping paths by using Monte-Carlo simulations for minimal cost flow as explained in the following section in detail. It is believed that the present investigations contribute to the current efforts in particle sorting, trapping and assembling in the areas of micro-manufacturing, microfluidics, regenerative medicine and biotechnology.

---

2. Materials and Methods

---

2.1. An Assignment Problem: Euclidean Bipartite Matching

In the present study, an assignment problem, to be specific Euclidean bipartite matching problem, is investigated so as to minimize the total length of the paths during particle positioning and assembly. In this type of problem, the particles in the initial configuration, denoted with p, and final configurations, denoted with q, with the set length of N have one-to-one correspondence. The cost function for particle paths is defined through Euclidean distance of each particle between the initial and final configurations, which results in N × N cost matrix considering each possible particle match between initial and final configurations. Then, the minimal cost flow is calculated via the optimal permutation based on the total Euclidean distance of particles ^[12,13,14]. Mathematically speaking,

$T = \min \sum\limits_\Pi {{\bf{d}}\left( {p,q} \right)}$

(1)

for which d is the Euclidean distance function for two points, T is the total Euclidean distance and $\Pi$ is the permutations for one-to-one correspondence. Under these circumstances, there should be only one matching pair for each p and q, otherwise, one-to-one correspondence is violated. It is also noteworthy that non-overlapping condition of the paths should be satisfied for an optimal solution.

---

2.2. Monte-Carlo Simulations for Minimal Cost Flow

In order to solve the problem given in Eq. (1), a cost flow matrix is formed where the aim is to find a flow of minimal total cost from the particle set in the initial configuration to the assembled particle set, such that

$\left[ {\begin{array}{*{20}{c}} {{\bf{d}}\left( {{p_1},{q_1}} \right)}&{{\bf{d}}\left( {{p_1},{q_2}} \right)}& \cdots &{{\bf{d}}\left( {{p_1},{q_n}} \right)}\\ {{\bf{d}}\left( {{p_2},{q_1}} \right)}& \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots \\ {{\bf{d}}\left( {{p_n},{q_1}} \right)}& \cdots & \cdots &{{\bf{d}}\left( {{p_n},{q_n}} \right)} \end{array}} \right].$

(2)

Thereafter, Monte-Carlo simulations are carried out by random choice of elements from each row. Here, one-to-one correspondence is provided by selecting a column not used previously in each new row. Otherwise, for instance, two or more particles in the initial configuration may end up with having a same particle match in the final configuration, which is not physically possible. This random but constrained element selection is followed by finding and sorting the permutations giving the non-overlapping paths with the minimal total Euclidean distance.

---

3. Results and Discussion

---

3.1. Global Minimum Versus Local Minima

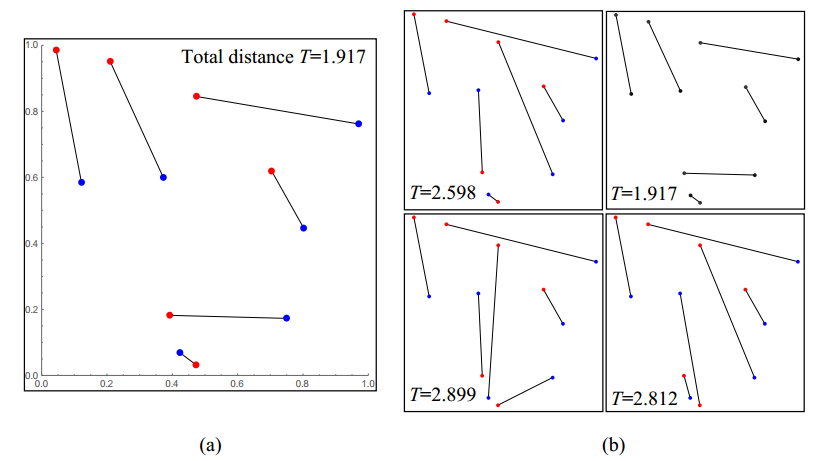
For comparing the global minimum and local minima of the problem, two sets of random points with same size N = 6, were generated in a domain of $\Omega = \left[ {0, 1} \right] \times \left[ {0, 1} \right]$. In order to obtain the global minimum, all the possible permutations were checked, which provides one-to-one correspondence and minimizes the total Euclidean distance. It is noteworthy that for the global minimum, path overlapping constraint seems to be redundant. Similarly, Monte-Carlo simulations were run on an Intel i7 (2.6 GHz) and 8 GB RAM to determine the local minima for the same problem. Figure 2 depicts the paths, minimized total distances T and computation times t for the problems.

---

3.2. Infinitesimal Particle Assemblies

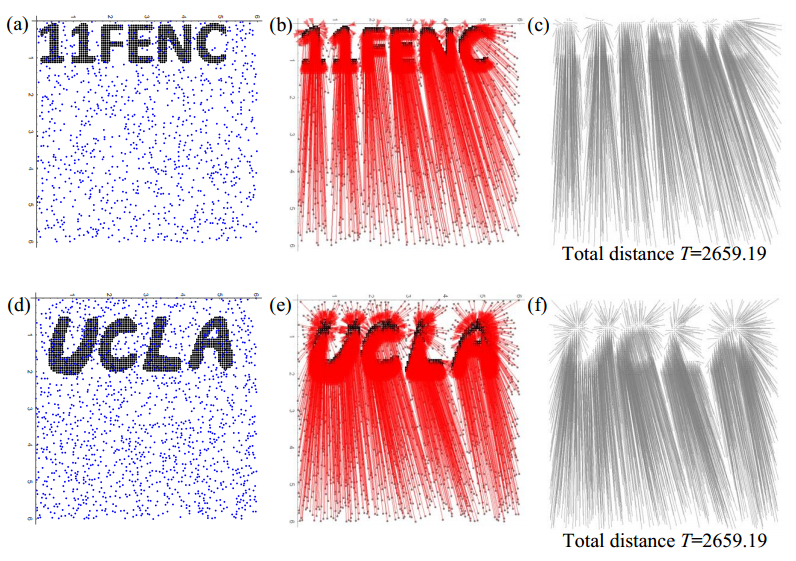
The algorithm was extended to form particle assemblies, for which various figures were separated to their morphological components following the image processing procedures provided in the literature ^[15]. In these case studies, the particles were assumed to be infinitesimal for the sake of bipartite matching. First, symbol with one morphological component (hand written E) and one with two morphological components (computer generated A) were studied in $\Omega = \left[ {0, 7.5} \right] \times \left[ {0, 7.5} \right]$. Here, morphological component refers to an array in which each pixel of image is replaced by an integer index representing the connected foreground image component in which the pixel lies ^[16,17]. In order to form the assembly, a hologram was generated, i.e., blue regions depicted in Figure 3(a) and 3(c), then number of particles N was computed. Then, these N particles were randomly selected from the uniformly distributed set in the given Ω. Finally, the algorithm was implemented to determine the particle paths between the randomly selected and assembled particles of the hologram, as depicted in Figure 3.

In addition to this, number and letter combinations including one (computer generated 11FENC) and multi (hand written UCLA) morphological components were also illustrated in Figure 4.

---

3.3. Real-sized Particle Assemblies

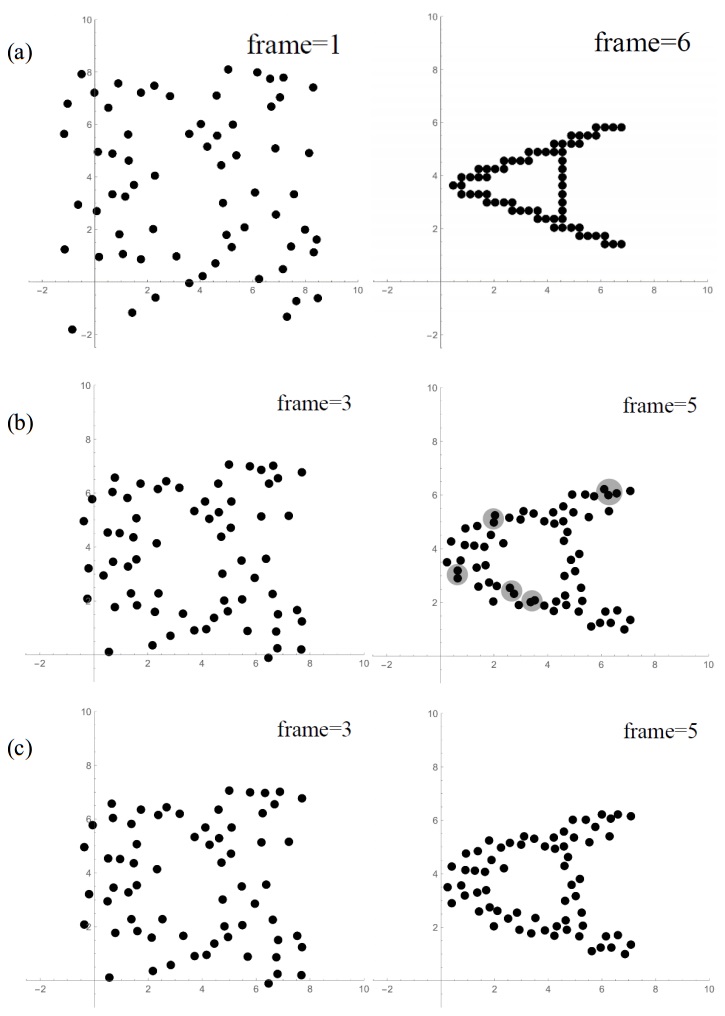
In addition to infinitesimal particles, path-planning algorithm was further improved for real-sized particle assemblies. Similar to the present bipartite matching algorithm, this novel approach uses Monte-Carlo simulations to detect the colliding particle matches and then swap their target destinations in the final configuration. Thus, a solution is sought after iteratively in order to prevent particle collisions. For this purpose, first, the bipartite matching algorithm was used to define the paths and motions of the particles. Then, motion frames were iteratively checked to plan the path in a realistic manner. In Figure 5, an illustration of the path planning and corrections due to collisions of particles with radius of 0.315 are depicted, for which 6 frames were analyzed in total.

---

4. Conclusions

In the present study, an assignment problem, to be specific Euclidean bipartite matching problem, is investigated so as to minimize the total length of the paths during particle positioning and assembly. For this problem, a cost matrix is generated for the possible matches between initial (random selection) and final (assembly) configurations of the particles. Thereafter, Monte-Carlo simulations are carried out with constrained element selection based on non-overlapping particle paths and sorted with the minimal total Euclidean distance. The results show that proposed method works reasonably for particle assemblies with several components. However, further improvements include clever iteration strategies for determining the global minimum, e.g., combination of Monte-Carlo simulations with available combinatorial optimization algorithms, further developments in path planning of real-sized particle assemblies for complicated geometries, and generation of three dimensional particle assemblies with optimal paths by using the same methodology.

---

Acknowledgments

A.K. gratefully acknowledges the financial support of Tekniikan edistämissäätiö TES through Foundations' Post Doc Pool, Finland.

---

Conflict of Interest

There is no conflict of interest.

---