1. Introduction
The global trend of miniaturization in modern semiconductor manufacturing continues to stimulate new applications of spectroscopic ellipsometry (SE). For instance, the presence of electrically active defects in thin oxide layers of semiconductor devices limits their performance and reliability. In recent years, a few papers were dedicated to application of spectroscopic ellipsometry to diagnose and characterize charge trapping defects in thin dielectric film stacks [1,2,3,4,5,6,7,8,9,10]. Indeed, spectroscopic ellipsometry, as well-established and widely used in-line characterization technique in semiconductor volume manufacturing, can provide one of the ways to monitor noninvasively the presence of dislocations and defects in large densities during semiconductor device fabrication.
Meanwhile, SE has an indirect nature and requires appropriate modeling analysis to interpret optical measurements and extract useful information. In particular, this analysis demands a suitable optical model consisted of the optical properties of materials (the complex refractive index N = n + ik or the dielectric function ε = ε1 + iε2) and thickness (or other topographic parameters) of each layer for a structure under investigation. In the simplest case, tabulated data for the n&k's of each layer can be used as inputs for the optical model. On the one hand, this assumption may seem natural and advantageous since it does not overcomplicate the model. However, in practice, even relatively small deviations in material optical properties (from nominal model inputs) due to process condition variations may significantly affect the measurement results. Moreover, the material optical properties might be unknown a priori and need to be determined during characterization. In that situation, when the optical constants are not really “constant”, i.e., fixed and invariable, and/or not established beforehand, modeling or parameterization of the material n&k's becomes an absolute necessity [11,12,13] and for this purpose many analytical physics-based and Kramers-Kronig consistent expressions (models) have been developed which describe various types of materials—amorphous and crystalline semiconductors and dielectrics, metals, organic films, optical metamaterials, etc.
However, in some cases current parametric models cannot be used adequately since they do not account for discrete absorption features below the bandgap which can be associated with defects or film structural changes [1,5,7,14,15]. Instead, one can use so-called “point-by-point data inversion” method (also known as “direct data inversion” or “exact numerical inversion”) to represent the dielectric function. In a point-by-point inversion procedure the n&k's dependency on each other at different wavelengths is disregarded, all variables in the optical model are fixed except the n&k values for analyzable material at each wavelength λ (or ε1 and ε2, i.e., the real and imaginary part of the dielectric function at each photon energy E) and values for n and k at each wavelength are calculated from the measured ellipsometric parameters Psi (Ψ) and Delta (Δ). Obviously, the point-by-point method should be used with great caution. First of all, the correct initial model must be used for such direct data inversion, i.e., all other parameters, except the n&k values for the material under study, need to be known with high accuracy, otherwise those modeling errors can lead to unphysical dispersion or discontinuities in the optical constants. Moreover, existing measurement noise will be directly translated into extracted n&k values. Even more importantly, the method does not enforce Kramers-Kronig consistency between the real and imaginary part of the obtained optical constants (or, dielectric function) and, therefore, can result in unphysical shape of the (n, k)-curve in the considered spectral range. Of course, this approach is not appropriate for all applications and the physics-based oscillator models with physically meaningful parameters should still be preferable since they can provide further insights into other important material properties such as composition, phase structure, doping, stress, uniformity, electrical properties, etc.
Almost 20 years ago, Jellison, Jr. and Modine suggested new optical function parameterization, namely so-called Tauc-Lorentz (TL) oscillator model [16], which quickly became very popular parameterization for the dielectric functions of amorphous semiconductors and dielectrics. Original version of the model was proposed for single interband transition, i.e., the imaginary part of the dielectric function ε2 near the band edge was expressed as single TL oscillator:
|
ε2(E)={AE0C(E−Eg)2(E2−E20)2+C2E21E,E>Eg,0,E≤Eg,
|
(1) |
where
Eg is the bandgap of the material,
A is the oscillator amplitude,
E0 is the energy (position) of the Lorentz peak, and
C is the broadening parameter. Nevertheless, very often in practice it is necessary to generalize the model for a case of multiple TL oscillators to describe more accurately the optical properties of various materials. But more often than not these multi-oscillator implementations incorporate
different band-gap parameters
Eg and, therefore, violate a physicality of the dispersion model which assumes a uniqueness requirement for the band-gap value.
Here we apply a modified Tauc-Lorentz dispersion model with common band-gap parameter Eg and possibility to represent reasonably the absorption features below the bandgap. We illustrate our approach with a few examples of the dielectric function parameterization. These examples have been selected for their relevance to some practical circumstances in material characterization for modern technological applications. We expect that this approach will increase the accuracy of estimation of the optical functions to meet the needs in many practical situations in the microelectronic industry.
2. Model Description
A well-known problem with the application of the TL model to thin films is that it explicitly neglects the absorption below Eg, i.e., ε2(E) = 0 for E ≤ Eg, which makes the modeling of the optical spectra for some materials in the vicinity of the absorption edge problematic [15]. Typically, the sub-band absorption is modeled by combining the exponential Urbach tail
|
ε2(E)=E1Eexp{E−EtEu}(0<E≤Et),
|
(2) |
where
Et denotes the demarcation energy between the Urbach tail transitions and the interband transitions and
Eu is the so-called Urbach energy, representing the width of tail states in the forbidden gap, with the TL oscillator
[17,18,19,20]. In some cases, this approach demonstrated an improved description of the optical dielectric response for the materials such as, for example, high-
κ dielectric films
[15,21,22], hydrogenated amorphous silicon nitride (a-SiN
x:H) films
[23] and titanium dioxide (TiO
2) thin films
[24,25]. However, the absorption below the band gap often does not correspond to the Urbach tail and the simple combination of Eq. (2) with the TL oscillator(s) is insufficient. In our approach, the imaginary part of dielectric function
ε2 includes not only the TL oscillator(s) with
E0j >
Eg but also an ensemble of free/unbounded Lorentz and/or Gaussian oscillators. Importantly, the band-gap parameter
Eg is set to be the same for all TL oscillators. Thus, the imaginary part of the dielectric function
ε2 in TLLG model is defined as follows:
|
ε2(E)=GT(E)Lb(E)+Lf(E)+Gf(E),
|
(3) |
where
GT(
E) in the first term represents the Tauc gap function
|
GT(E)={(E−Eg)2E2,E>Eg,0,E≤Eg,
|
(4) |
Lb(
E) and
Lf (
E) are set as the sum of the bounded or free/unbounded Lorentz oscillators
|
L(b,f)(E)=∑jAjE0jC2jE(E2−E20j)2+C2jE2,
|
(5) |
where
E0j <
Eg for free/unbounded Lorentz oscillators, and
Gf (
E) is the set of the Gaussian oscillators
[26,27]
|
Gf(E)=∑jAj{exp[−(E−E0jCj)2]−exp[−(E+E0jCj)2]}
|
(6) |
(the Gaussian oscillators can be placed below as well as above
Eg).
The real part of the dielectric function ε1 for the TLLG oscillator model is obtained by the Kramers-Kronig integration of the ε2 function described by Eq. (3):
|
ε1(E)=ε∞+2πP∫∞Egξε2(ξ)ξ2−E2dξ,
|
(7) |
where
ε∞ represents the value of real part of the dielectric function
ε at infinite energy and it is an additional fitting parameter in the oscillator model, the
P stands for the Cauchy principal part of the integral. The TLLG model is implemented in OLSA (Off-Line Spectral Analysis), a software package for the development and optimization of film dispersion models, available from KLA-Tencor Corporation (Milpitas, CA, U.S.A.).
3. Results and Discussion
3.1. Interfacial defects in SiO2 layer
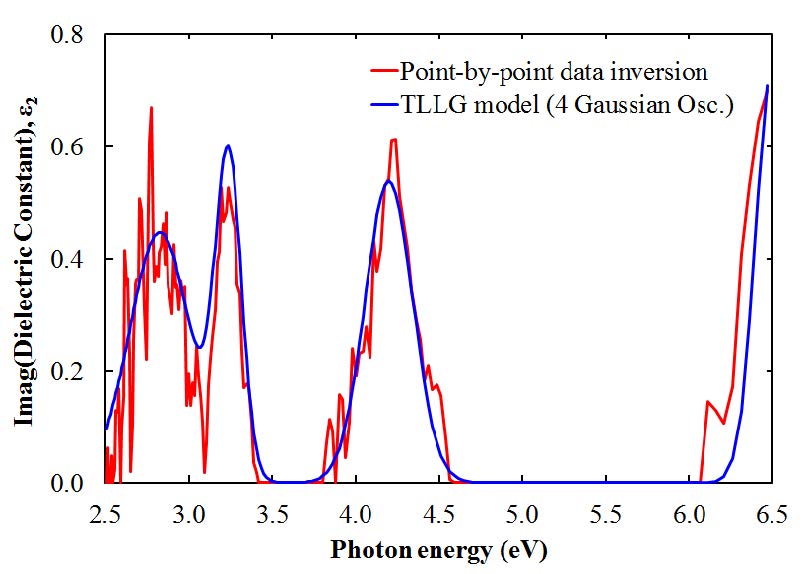
Figure 1 shows the imaginary part of the dielectric function ε2 for ~20 Å thick gate oxide and its parameterization by the TLLG model with four Gaussian oscillators (no TL oscillators was used in that case since the oxide’s optical absorption edge is outside our measurement range). These results were obtained from ex situ spectroscopic ellipsometry measurements performed at room temperature using research-grade rotating-compensator spectroscopic ellipsometer M-2000® from J.A. Woollam Co., Inc. in the spectral region of 192-1678 nm (0.74-6.47 eV) at several angles of incidence (50-75°). All ellipsometric measured data were analyzed using the wavelength point-by-point extraction procedure as well as the TLLG oscillator model which results in four sub-bandgap discrete absorption features with Gaussian line shapes located at 2.82, 3.24, 4.20, and 6.50 eV (Table 1). First absorption peak corresponds to a localized defect in Si/SiO2 film system which has been observed first by Price et al. [7] and most likely associated with a positively charged oxygen vacancy. Two other absorption features nearly coincide with the energies of critical points E0' and E2 of silicon (E0'~3.30 eV, E2~4.25 eV [28]; E0'~3.320 eV, E2~4.270 eV, E1'~5.317 eV [29]; E0~3.316 eV, E2~4.248 eV [30]). It is believed that the appearance of these absorption bands can be associated with inaccuracy of the model used for point-by-point data inversion [3]. The absorption band at ~6.5 eV has been previously detected [31,32,33] and attributed to a Si-Si-Si structure, an oxygen-deficiency related defect, in the oxide film.
Table 1. TLLG model parameters for ~ 20 Å thick gate oxide.
| Model parameter | Gaussian Oscillator # |
| 1 | 2 | 3 | 4 |
| A (d.u.)* | 0.4467 | 0.5651 | 0.5385 | 0.7485 |
| E0 (eV) | 2.8249 | 3.2371 | 4.1995 | 6.5034 |
| C (eV) | 0.2594 | 0.1115 | 0.2029 | 0.1441 |
| *the abbreviation for dimensionless units |
No prominent absorption features at 3.6 eV and 3.9 eV, observed in Ref. 7, as well as absorption peak at 4.75 eV, detected in Ref. 9 for the Si/SiO2 stack, were observed in this study. Absence of those absorption features may be explained by many factors such as different substrate surface conditions or quality of the gate oxide layer.
3.2. Sub-bandgap absorption features in hafnium oxide (HfO2) and hafnium aluminate (HfAlO)
Hf-based high-κ dielectric oxides are widely employed for a variety of applications (a replacement for SiO2 as a gate insulator, transparent optical coatings with tunable electrical conductivity, high-κ dielectrics in capacitors, insulating barriers in tunnel junctions, planar waveguides and as an etch-stop layer for phase-shifting masks, etc.) in microelectronic, photovoltaic and optoelectronic industries. Multiple studies on the hafnium dioxide HfO2 optical properties have reported the presence of an absorption feature 0.2-0.3 eV below the optical band-gap energy Eg and attributed this feature to the hafnium dioxide crystallinity or, in particular, to monoclinic phase of HfO2 [1,2,8,14,15,34,35,36,37,38,39,40,41]. Similar sub-bandgap absorption feature has been also reported for atomic-layer-deposited (ALD) aluminum oxide Al2O3 [42].
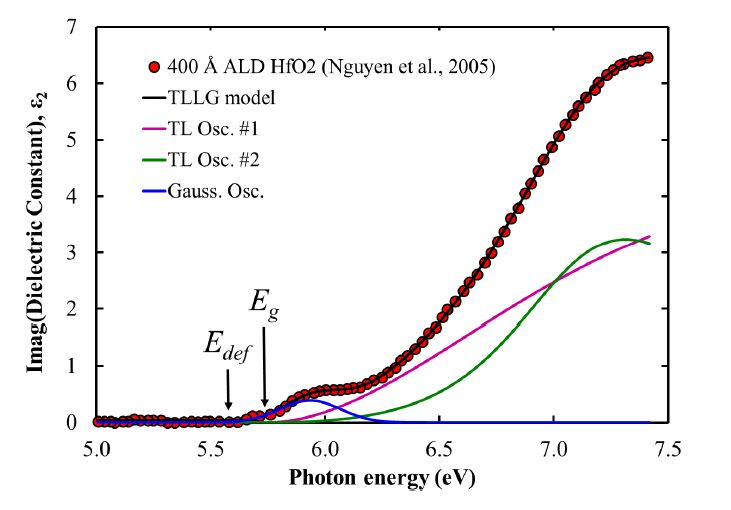
Nguyen et al. [2] determined the energy parameters for high-quality HfO2 and HfSiO films from vacuum-ultraviolet SE data by plotting the empirical expression (n(E)α(E)E)1/2 versus E and linearly extrapolating it to (n(E)α(E)E)1/2 = 0 (the Tauc plot method), where n, α, and E are the index of refraction, the absorption coefficient, and the photon energy, respectively. The dielectric function ε was extracted by inverting the ellipsometric data at each wavelength (“point-by-point data inversion”). For the 400 Å thick ALD HfO2 the following values have been obtained: Eg = 5.80 ± 0.05 eV and Edef = 5.60 eV, where Edef is the “defect” feature energy (herein, the appearance of the sub-bandgap absorption feature).
We applied the TLLG model to fit ε2 spectrum extracted by Nguyen et al. [2]. Figure 2 shows the imaginary part of the HfO2 dielectric function ε2 and its parameterization by combination of two TL oscillators with Gaussian function. Table 2 summarizes the best-fit parameters for the 400 Å thick HfO2 film. The TLLG model gives the following energy parameters: Eg = 5.74 eV, Edef = 5.57 eV. The value of energy bandgap parameter obtained from the TLLG model is similar to that from the Tauc plot method (as already pointed out by Di et al. [43] for the case of ordinary TL model). Thus, the TLLG model adequately describes the sub-band absorption features observed in HfO2 thin films in contrast to Refs. 15, 38 where this specific shape absorption has been incorrectly associated with the exponential Urbach tail (as it was also previously noted by Franta et al. [44]).
Table 2. TLLG model parameters for 400 Å thick HfO2 film.
| Model parameter | Oscillator Type |
| TL #1 | TL #2 | Gaussian |
| A (eV) | 449.5 | 95.54 | 0.394 (d.u.) |
| E0 (eV) | 6.140 | 7.131 | 5.935 |
| C (eV) | 4.601 | 1.226 | 0.312 |
| Eg (eV) | 5.741 | 5.741 | n/a |
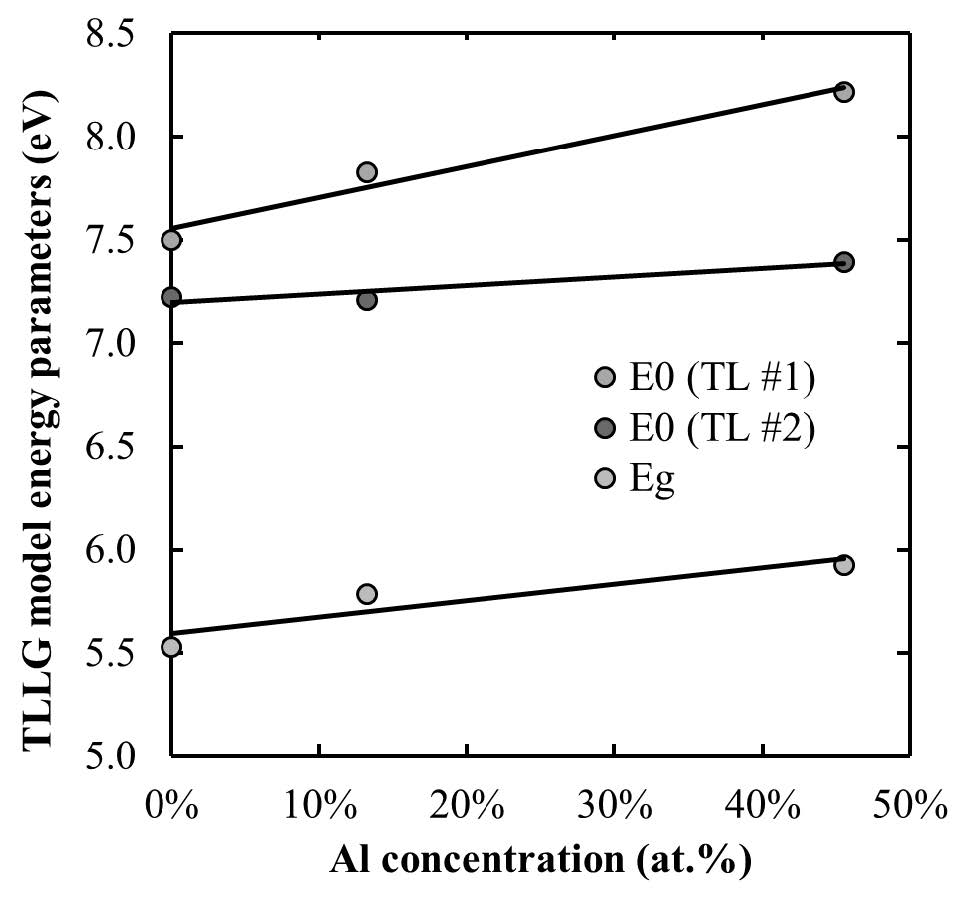
Moreover, our results show a correlation between not only the energy band gap but also the bounded oscillators positions (E0j), obtained from the TLLG model, to other important material properties such as composition, phase structure, doping, stress, etc. As an example, we applied the model to fit ε2 spectrum for the hafnium aluminate (HfAlO) films with various Al concentration extracted by Nguyen et al. [45]. The best-fit parameters of TLLG model for the set of HfAlO thin films are listed in Table 3. Figure 3 shows a plot of the TLLG model energy parameters E0 for two TL oscillators as well as Eg versus the aluminium concentration for the samples of the HfAlO thin films. This relatively weak linear variation of Eg is consistent with the results reported in Ref. 46. Besides that, the position of one of the TL oscillators (first E0 in our model) also linearly depends on the aluminium content and this relation can be considered as a quantitative measure for the characterisation of the HfAlO thin films using optical spectroscopic measurements. Note that the variation in oscillator position E0 is even more pronounced than the increase in band-gap energy Eg (see Figure 3) (a little effect of Al on the band gap of HfO2 was also reported in a few papers [47,48]).
Table 3. TLLG model parameters for the samples of HfAlO thin films.
| Model parameter | Al concentration (at.%) |
| 0.0 | 13.2 | 45.5 |
| ATL1 (eV) | 113.7 | 92.88 | 52.01 |
| ATL2 (eV) | 24.34 | 31.32 | 28.91 |
| AG (d.u.) | 0.274 | 0.286 | 0.273 |
| E0 TL1 (eV) | 7.50 | 7.83 | 8.22 |
| E0 TL2 (eV) | 7.22 | 7.21 | 7.39 |
| E0 G (eV) | 5.84 | 6.24 | 6.36 |
| CTL1 (eV) | 4.83 | 4.06 | 2.83 |
| CTL2 (eV) | 1.14 | 1.74 | 1.61 |
| CG (eV) | 0.648 | 0.818 | 0.809 |
| Eg (eV) | 5.53 | 5.79 | 5.93 |
3.3. Modeling of the UOx dielectric function near the optical absorption edge
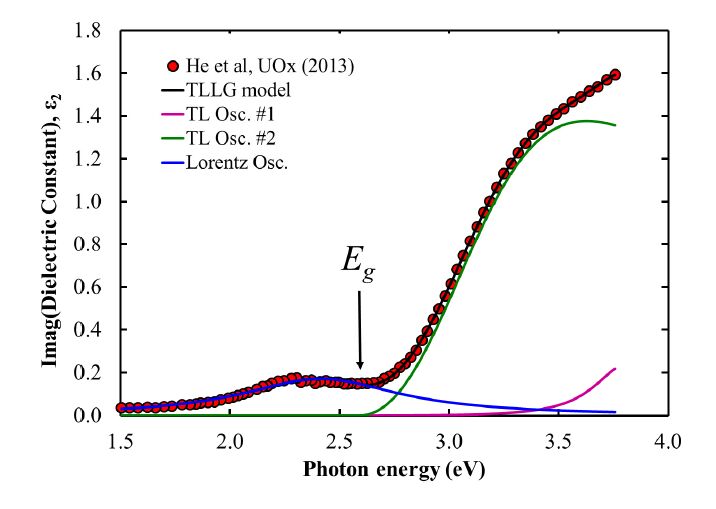
Uranium oxides are not only used in nuclear industry but due to their interesting electronic and electro-optical properties have been studied for other potential applications which include manufacturing of highly reflective multilayer mirrors for the extreme ultraviolet region, photo-anodes in photoelectrochemical cells for solar-assisted hydrogen production, efficient solar cells and fabrication of certain active electronic devices (a Schottky diode and a bipolar p-n-p transistor) [49,50,51]. The optical properties of the uranium oxide films deposited by magnetron sputtering were determined over different spectral ranges by spectroscopic ellipsometry in Refs. 52, 53. The UOx dielectric functions in these references were obtained by applying the Drude-Lorentz model [52] and point-by-point data inversion [53] (the latter uses six different methods of the band gap determination based on linear extrapolation of various functional dependences for ε2 and the absorption coefficient α).
Here we used the TLLG model to fit ε2 spectrum extracted by He et al. [53]. A combination of two TL oscillators with common Eg and Lorentz function was used to fit the UOx optical properties (Figure 4). Table 4 summarizes the best-fit parameters for ~1000 Å thick UOx film. Using the TLLG model, the value of energy bandgap parameter was determined to be Eg = 2.59 eV which is slightly smaller than the value obtained by the Tauc plot method (Eg = 2.64 ± 0.02 eV, Ref. 53) and very close to the band-gap energy of 2.61 eV determined in Ref. 54 for α-UO3, the α-phase of uranium trioxide, a “non-traditional” semiconducting material. Note that the Lorentz function worked better than Gaussian one in fitting the broad sub-band feature below bandgap Eg.
Table 4. TLLG model parameters for ~1000 Å thick UOx film.
| Model parameter | Oscillator Type |
| TL #1 | TL #2 | Lorentz |
| A (eV) | 0.937 | 41.30 | 0.170 (d.u.) |
| E0 (eV) | 3.805 | 3.105 | 2.454 |
| C (eV) | 0.396 | 1.456 | 0.888 |
| Eg (eV) | 2.590 | 2.590 | n/a |
4. Conclusion
The physics-based parameterization of the dielectric functions of various materials is one of the most commonly used approaches in current optical metrology, in particularly, in spectroscopic ellipsometry. The reason is that a broad range of important material properties can be characterized based on physically meaningful parameters of the optical model for the dielectric function. One of the most widely used for amorphous materials is the Tauc-Lorentz oscillator model which, however, is not always correctly implemented and also explicitly neglects the absorption below the bandgap. In this paper, a modified Tauc-Lorentz dispersion model with common band-gap parameter Eg and possibility to represent reasonably the absorption features below the bandgap was applied to dielectric function parameterization near the optical absorption edge and sub-bandgap absorption features in the Si/SiO2 film system as well as in hafnium dioxide HfO2 and uranium oxide UOx thin films. The model is flexible enough to adequately portray the dielectric functions for a wide variety of materials. This should facilitate the study of process-induced defects and/or interface states in thin dielectric films as well as electronic excitations in thin organic films via spectroscopic measurements. The most obvious improvement of the proposed model would be replacement of separate unbounded Lorentz and Gaussian oscillators by a generalized Gauss-Lorentz dispersion model in which the oscillator broadening varies smoothly between Lorentzian and Gaussian types via adjustment of an additional shape parameter.
Acknowledgments
The authors wish to acknowledge support and collaboration among GLOBALFOUNDRIES and KLA-Tencor Corp.
Conflict of Interest
The authors declare that there are no conflicts of interest related to this study.









 DownLoad:
DownLoad: