Citation: Jing Chen, Ben J. Hanson, Melissa A. Pasquinelli. Molecular Dynamics Simulations for Predicting Surface Wetting[J]. AIMS Materials Science, 2014, 1(2): 121-131. doi: 10.3934/matersci.2014.2.121
| [1] | Samaneh Nasiri, Michael Zaiser . Rupture of graphene sheets with randomly distributed defects. AIMS Materials Science, 2016, 3(4): 1340-1349. doi: 10.3934/matersci.2016.4.1340 |
| [2] | Roman Koleňák, Igor Kostolný . Investigation of microstructure and wettability of selected lead-free solders for higher application temperatures. AIMS Materials Science, 2018, 5(5): 889-901. doi: 10.3934/matersci.2018.5.889 |
| [3] | Mica Grujicic, Jennifer S. Snipes, S. Ramaswami . Polyurea/Fused-silica interfacial decohesion induced by impinging tensile stress-waves. AIMS Materials Science, 2016, 3(2): 486-507. doi: 10.3934/matersci.2016.2.486 |
| [4] | Julian Konrad, Dirk Zahn . Assessing the mechanical properties of molecular materials from atomic simulation. AIMS Materials Science, 2021, 8(6): 867-880. doi: 10.3934/matersci.2021053 |
| [5] | Koufos Evan, Muralidharan Bharatram, Dutt Meenakshi . Computational Design of Multi-component Bio-Inspired Bilayer Membranes. AIMS Materials Science, 2014, 1(2): 103-120. doi: 10.3934/matersci.2014.2.103 |
| [6] | Nilesh Shahapure, Dattaji Shinde, Ajit Kelkar . Atomistic modeling and molecular dynamic simulation of polymer nanocomposites for thermal and mechanical property characterization: A review. AIMS Materials Science, 2023, 10(2): 249-287. doi: 10.3934/matersci.2023014 |
| [7] | Clara Argerich, Ruben Ibáñez, Angel León, Anaïs Barasinski, Emmanuelle Abisset-Chavanne, Francisco Chinesta . Tape surface characterization and classification in automated tape placement processability: Modeling and numerical analysis. AIMS Materials Science, 2018, 5(5): 870-888. doi: 10.3934/matersci.2018.5.870 |
| [8] | Andrzej Eilmes . Ion aggregation in complexes of alkali metal iodides and poly(ethylene oxide) or pentaglyme studied by molecular dynamics. AIMS Materials Science, 2020, 7(5): 632-649. doi: 10.3934/matersci.2020.5.632 |
| [9] | Zhimin Cao, Chenhui Xu, Caiwei Xiao, Wei Liu, Jiaohu Huang, Wenjun Zong, Junjie Zhang, Tao Sun . Molecular dynamics study of mechanical properties of HMX–PS interface. AIMS Materials Science, 2019, 6(1): 111-118. doi: 10.3934/matersci.2019.1.111 |
| [10] | Wisatre Kongcharoensuntorn, Pornpen Atorngitjawat . Influence of chlorotrifluoroethylene on crystal structure and polymer dynamics of poly(vinylidenefluoride-co-chlorotrifluoroethylene) antibacterial copolymers. AIMS Materials Science, 2023, 10(1): 164-181. doi: 10.3934/matersci.2023009 |
“Wetting” is the ability of a liquid to maintain contact with a solid surface through intermolecular interactions. In other words, wetting is the balance between adhesive and cohesive forces; cohesive forces within a liquid cause it to avoid contact with the surface by forming a spherical shape when all three phases are in equilibrium, whereas adhesive forces between the liquid and the solid surface cause the liquid to spread across the surface. If a surface of a material is attracted to a certain liquid, it is considered to be “-philic” for that substance; for example, a surface that is attracted to water is called “hydrophilic”, and attracted to oil is called “oleophilic”. However, if a surface tends to repel a certain liquid, it is considered to be “-phobic” for that substance; for example, “hydrophobic” and “oleophobic” mean that the surface repels water or oil, respectively.
Thus, the goal of this report is to survey the use of molecular dynamics (MD) simulations for investigating the wetting behavior of liquids on solid surfaces at the nanoscale by calculating both the surface tensions of solids and liquids and contact angles of liquid nanodroplets on surfaces with molecular scale roughness. This work is first put into the context of what is done experimentally via wetting models for solid surfaces interacting with liquid droplets.
The wettability of a surface is determined experimentally by placing a droplet of liquid on the surface and measuring the apparent contact angle (θ), which is defined as the angle formed between the solid/liquid interface and the tangent line of the vapor/liquid interface [1] and is depicted in Figure 1. Assuming that the liquid is water, if the apparent θ is smaller than 90˚, the surface is considered to have high wettability, or hydrophilic; larger than 90˚ is considered low wettability, or hydrophobic; and over 150˚, the surface is classified as superhydrophobic [2, 3]. These terms are defined similarly for other types of liquids.
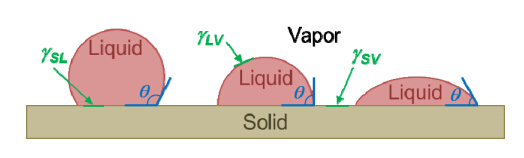 Figure 1. Wetting characteristics of a solid surface, from low wettability (left) to high wettability (right).
Figure 1. Wetting characteristics of a solid surface, from low wettability (left) to high wettability (right).
When the solid surface is perfectly flat, rigid, smooth and chemically homogenous (in other words, an ideal surface), the contact angle obtained from the droplet is called Young’s contact angle, which is related to the surface tension (g) of each substance through the following formula [4],
| γSV =γSL+γLVcosθ | (1) |
where gSV is the surface tension between the solid and gas (vapor), gSL is between solid and liquid, and gLV is between liquid and gas. In general, θ increases when γLV decreases; in other words, the lower γLV is, the easier it is for that liquid to wet the surface [5]. Thus, lowering γSV will be useful in order to obtain better hydrophobicity and even superhydrophobicity; however there is a limitation to the lowest g that a material can possess. For organic liquids with a much lower g, only decreasing g of the surface has been observed to not be enough to achieve superoleophobicity [2, 6]. Note that g for a substance is comprised of all of the different intermolecular interactions (cohesive forces) that exist within a substance, according to the Fowkes equation [7, 8],
| γ=γD+γP+γind+γH+γm | (2) |
where γD is the contribution due to dispersion (van der Waals) forces, γP is permanent dipoles, γind is induced dipoles (polarizability), γH is hydrogen bonding, and γm is metallic interactions.
Real surfaces do not exhibit perfect smoothness, rigidity, or chemical homogeneity, and thus other models have been developed to take these effects into account. One consequence is contact angle hysteresis (H) [1, 3] that occurs because there are a range of thermodynamically stable θ values (called metastable states) that may exist. H is thus defined as the difference between the maximum stable angle, called the advancing contact angle (qa), and the minimum stable angle, or the receding contact angle (qr), which are commonly measured on a sloped plane. In addition, surface roughness plays a significant role [1, 9, 10]. For example, the lotus leaf exhibits superhydrophobicity, and scanning electron microscopy (SEM) images revealed that a lotus leaf contains not only primary protuberances at the microscale but also each protuberance is comprised of secondary rough structures on its surface [11]. In terms of surface roughness, there are two types of wetting regimes. One regime is the heterogeneous wetting regime, where a gas (often air) fills the spaces created by the rough texture rather than the liquid, and thus the liquid-solid contact line also contains liquid-gas and solid-gas contacts. This regime is described by the Cassie-Baxter model, given by the following, [9]
| cosθ∗=rfcosθ+f−1 | (3) |
wherer is the ratio of the true area of the solid surface that is wet to the apparent contact area if it were perfectly smooth, and f is the fraction of the solid surface area that is wet by the liquid. The other regime is the homogeneous wetting regime, where the liquid completely fills the spaces created by the rough texture of the surface. This regime is described by the Wenzel model, which is obtained from Eq. 3 when f = 1 [12]. When θ is fixed, θ increases monotonously with f. In other words, the higher that f is, the lower that r will be. Thus, to find an optimized r is a major goal to design superhydrophobic and superoleophobic surfaces. Also, for the Wenzel model, the contact angle hysteresis will be very high, meaning that qr will be very low compared to qa [10], resulti ng in difficulties when removing a liquid from the surfaces when compared with the Cassie Baxter model, which performs much better in this aspect.
Experimentally, g of the surface can be tuned through surface modifications. For example, cotton was observed to achieve superhydrophobic and self-cleaning properties with treatment with a fluorosilane [13]. Treatment with fluorinated groups is effective for lowering g because fluorine has a small atomic radius and the largest electronegativity [14, 15, 16, 17]. Another widely used approach is to enhance the surface roughness with a fractal structure to improve the hydrophobicity of surfaces [2, 18, 19, 20]. Recently, Lee and coworkers designed and developed new anti-icing textile fabrics through the combination of lowering g and increasi ng surface roughness [6]; the results suggested that the apparent contact angle of water was 152-158˚, which also agreed with the prediction from the Cassie Baxter model, indicating that those treatments led to the fabric exhibiting superhydrophobicity.
Molecular dynamics (MD) simulations are comprised of the physical motions of atoms and molecules that are calculated by solving Newton’s equations of motion [21]. The forces are derived from the potential energy of the atoms within molecules that are comprised of both intramolecular and intermolecular forces. The intramolecular interactions are calculated based on the geometry of the molecule, such as bond energies, three body “bend angles”, and four body torsional angles, while the intramolecular interactions are a combination of van der Waals and electrostatic forces. By solving these equations at each time step, a time trajectory for a set of molecules can be calculated. MD simulations have provided a powerful tool for studying a variety of physical and mechanical properties, as this methodology provides a way to quantify the influence of atomic-scale interactions on larger scale properties. For example, MD simulations can predict surface characteristics such as wetting due to chemical modifications before applying the real treatments in the laboratory [22, 23, 24, 25].
As indicated in Figure 1 and Eq. 1, one critical interfacial property to characterize surface wetting is g. In an MD simulation, g can be calculated in several ways. One way is to calculate the excess energy between a molecular model of a surface (Esurface) and its corresponding bulk model (Ebulk), given by the following equation [26, 27, 28],
| γ=Esurface−EbulkA | (5) |
where A is the interfacial surface area of the surface. (Note that most MD simulation software outputs the energies on a per mole basis, and thus dimensional analysis may be necessary). Because the potential energy can be broken into the individual contributions due to factors such as hydrogen bonding and van der Waals interactions, MD simulations can provide additional insights into understanding g ( and thus the wettability) of a substance through the Fowkes relationship (Eq. 2), since those terms cannot be easily measured experimentally. Another way to calculate g from an MD simulation is by calculating the pressure profile using the following equation [29, 30],
| γ=12<Pzz−12(Pxx+Pyy)> | (5) |
where Pxx, Pyy and Pzz are the average pressures in the x, y and z dimensions, respectively. Finally, gSL is also directly proportional to the work of adhesion (Wadh) at the solid-liquid interface through the Dupre and Dupre-Young equations defined, respectively, as [7],
| WadhSL=γSV+γLV−γSL=γLV(1+cosθ) | (6a) |
In other words, Wadh describes the work required to separate the solid and liquid by creating unit areas of each (defined by gSV and gLV) but at the expense of the solid-liquid interface (gSL). Thus, a large positive Wadh value signifies strong adhesion between the solid and liquid, whereas a smaller positive value suggests weak adhesion; a negative value indicates repulsion, suggesting that the liquid will spontaneously separate from the solid. From an MD simulation, Wadh can be calculated from the following equation [31],
| Wadh=−EinterA=−[Etotal−(Esolid+Eliquid)]A | (7) |
The Einter term, which is the interaction energy between the solid and liquid, is calculated by first building a molecular model where the surface is completely covered with a liquid, and then calculating the total potential energy of the system (Etotal), as well as the total potential energy of the isolated solid (Esolid) and isolated liquid (Eliquid) components at a particular MD time step. This approach has been used to determine the relative differences for particular liquids interacting with surfaces based on different surface conditions such as patterning and roughness [32, 33, 34].
MD simulations have also been used to study wetting through the use of a liquid nanodroplet in contact with a surface. This technique is similar to the sessile drop technique used in physical experiments but on a different size scale. This calculation is generally done by first building a molecular model of a droplet of the liquid, and then equilibrating that droplet while it is in contact with a molecular model of a surface of interest with a particular degree of molecular surface roughness. Once a minimum energy state is achieved, the shape of the liquid is examined; if the liquid forms some sort of a spherical (or lenticular) shape, as with physical experiments, a static θ (depicted in Figure 1) may be calculated, and this value can be correlated with gSL via Eq. 1. As will be discussed below, there are some challenges with calculating θ from nanodroplets; however, these types of MD simulations have still provided some significant insights at the nanoscale on wetting characteristics that have complemented experiments.
One significant challenge with nanodroplets from MD simulations is that the conventional θ becomes ill-defined at the molecular level, even for smooth surfaces, as illustrated in Figure 2. However, different methods to approximately fit the outline of a droplet onto a spherical shape have been utilized [26, 35, 36, 37, 38, 39]. One approach is to neglect the liquid molecules that are closest to the surface, because there is frequently restructuring that occurs within the liquid molecules closest to the surface due to the strength of the interaction between the surface and the liquid; typically, this distance is 8 - 10 Å [40, 41, 42, 43]. This approach is done by physically drawing a line that is equal to the slope of the droplet just above the neglected thickness, then using this line to calculate the contact angle between the droplet and the surface. The advantage of this technique lies in its simplicity, as it only requires a liquid density profile and a way to draw a line. The disadvantage is the lack of an empiri cal method to verify the accuracy of the line placement, thus allowing for some error to enter into the calculation of θ. Considering the anisotropy of the wetting behavior, θ values are often calculated from different side views and averaged [25, 44].
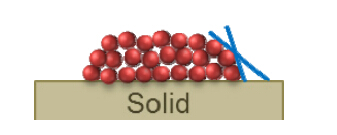 Figure 2. Depiction of the variation in the contact angle for a nanodroplet.
Figure 2. Depiction of the variation in the contact angle for a nanodroplet.
Another method that is widely used is to detect the shape of the droplet from the density profile [29, 37, 44, 45, 46]. For example, Giovambattista and coworkers [39] divided the droplet into slabs of width of 0.5 nm, separated vertically by 0.25 nm, and parallel to the surface; for each slab, they calculated the horizontal density profile. For each slab centered at the z axis, they associated a drop radius, rdrop (z), given by the distance at which the horizontal density profile falls to 0.2 g/cm3. The contact angle is obtained from the droplet profiles by fitting the curves with a quadratic function. By this method, the authors achieved smoother curves of the outline of the droplet and then measured the contact angles from it. Another method was based on a mathematical relation between the average height of the center of mass of the water droplet (<zc.m.>) and contact angle, given by the following equation [37],
| <zc.m.>=2−4/3R0(1−cosθ2+cosθ)1/33+cosθ2+cosθ | (8) |
where R0 is the radius of an isolated spherical droplet of N water molecules.
Another challenge with correlating MD simulations to experimental results is that there is no consistent methodology for the preparation of the droplet or the surface, and using different initial configurations can cause a wide disparity in the resulting values. An example of this disparity is the wide range in published values for θ of water on graphene from both experiments and simulations, which range from 29° to 115°, with the most common range reported being in the range of 84°-86° [47]. Studies have indicated that basic system parameters such as the size of the nanodroplet can have an influence on the calculated θ values. In a study of θ of water on a gold substrate, Wu and coworkers [48]determined that changing the droplet diameter from 4.5 nm to 7.5 nm resulted in a change in θ from 54° to 117°. This dependence on the droplet size makes it difficult to compare reported θ values without a consistent droplet size.
Even the formation and placement of the droplet on the surface is inconsistent among different studies. A common initial liquid configuration is to create a cubic simulation box of the liquid and , before placing the liquid in the interaction regime of the surface, allow the liquid to form a spherical shape through an MD simulation equilibration of just the liquid [39, 40, 41, 49, 50]. An alternative methodology is to equilibrate a cubic simulation cell of water at the desired temperature and pressure, and then placing this cube of water a small distance from the surface that has significantly larger dimensions [42, 51, 52, 53]; MD simulations are then applied to the combined system under the desired thermodynamic conditions for a period of time that is sufficient for enabling the cube to become a droplet interacting with the surface. Both methodologies seem to have their own advantages and disadvantages. The advantage of using the cubic liquid cell on the surface is the decrease in computational time as compared to the spherical nanodroplet on the surface. Alternatively, the advantage of using the spherical nanodroplet is that it is more representative of real world experimental conditions.
Despite these difficulties, MD simulations have provided insights at the nanoscale of what affects wetting behavior at the atomic level, like droplet size [25, 45], surface polarity [39], and surface structure [25, 26, 34]. The ability to easily make systematic small or large changes to the systems in MD simulations and to quantitatively calculate the influence of these gives an understanding of the mechanisms that govern surface wetting [25, 26, 35, 39, 54]. For example, although it is common to change the composition of the surface while keeping the nonbonded interaction parameters between the liquid and surfaced fixed, a number of studies have changed the strength of interaction between a liquid and a droplet through changing the strength of the nonbonded interaction parameters [32, 55, 56, 57]. MD simulations have also been used to examine surface properties such as surface roughness and their influence on the spreading of the nanodroplet [41, 58]. An extreme example of this modification is the formation of surfaces that are patterned with nanoscale grooves [59] or pillars [52]. The pattern can be easily modified to investigate the influence of the height and spacing of the grooves/pillars. The simulations allow for precise control of the placement of the droplet on the patterned surface, and allow for precise measurement of the extent to which the droplet penetrates the space between the groves/pillars, and thus a systematic investigation of the Wenzel versus the Cassie-Baxter models can be performed.
MD simulations have also been used to calculate the moving contact angle [40]. By applying a directional force to the liquid parallel to the surface, the droplet can be distorted similar to a droplet on an angled plane. The droplet no longer has a contact angle equal in all directions, but now has an advancing and receding contact angle. These two angles, specifically, the difference between these two angles, can be used to calculate the capillary number of the liquid with the surface; this number can be used to relate the strength of interaction between the liquid and the surface. By then removing the external force, the contact angle hysteresis may be investigated.
Finally, one adaptation of contact angle simulations with MD is its use to refine molecular mechanics force fields. For example, Jaffe and coworkers [32] used the contact angle between water and graphite to refine their existing force field parameters for carbon-water interactions. The authors began with established water (SPC/E) and carbon (continuum model) nonbonded parameters, and then they modified the cross-term nonbonded parameters between carbon and the oxygen in water to match the contact angles reported from experimental results. This example highlights the usefulness of the wettability calculations for also further improving computational results.
As technology advances, computational resources become significantly cheaper and more advanced, thus enabling the simulation of systems that are increasingly complex with less computational time. Larger droplets and surfaces could be used, negating some of the variations in droplet surface density in systems with a small number of liquid molecules. Additionally, increasingly complex computational models that account for forces such as polarization and droplet dynamics can be applied to the system and improve the accuracy and information garnered from the simulations.
By applying a force in a certain direction in simulations to mimic roll-off droplet experiments, it would be insightful to not only characterize advancing and receding contact angles, but to also quantify the amount of residue left by liquids in the process, or the robustness of the wettability [2]. In addition, as described above, the formation of a droplet on a surface is dependent on the interplay between the adhesion of the liquid with the surface and the cohesion of the liquid with itself. Typically most studies focus on the adhesion, neglecting further insight into the cohesion of the liquid and its effects. This area could be an interesting focus of future research, especially with the use of polarizable force fields. Finally, the environment of wetting in MD simulations is usually in vacuum, while in experiments they are conducted in air, and thus investigating how the wetting may be impacted by the incorporation of explicit gas molecules would be another useful future direction, especially in the context of the wetting models described by Eqs. 1-3.
This material was sponsored by the Defense Threat Reduction Agency - Joint Science and Technology Office for Chemical and Biological Defense (grant number HDTRA1-08-1-0049, HDTRA1-12-C-0048). The U.S. government is authorized to reproduce and distribute reprints for governmental purposes notwithst and ing any copyright notation thereon. DISTRIBUTION STATEMENT A. Approved for Public Release; Distribution is Unlimited. The authors would also like to thank Stephen Michielsen for the helpful discussions.
All authors declare no conflicts of interest in this paper.
| [1] | Callies M, Quere D (2005) On water repellency. Soft Matter 1(1): 55-61. |
| [2] | Tuteja A, Choi W, Ma M, et al. (2007) Designing superoleophobic surfaces. Science 318(5856):1618-1622. |
| [3] | Wang S, Jiang L (2007) Definition of superhydrophobic states. Adv Mater 19(21): 3423-3424. |
| [4] |
Young T (1805) An essay on the cohesion of fluids. Philosophical Transactions of the Royal Society of London 95: 65-87. doi: 10.1098/rstl.1805.0005

|
| [5] | 6. Lee HJ (2012) Design and development of anti-icing textile surfaces. J Mater Sci 47(13):14-5120. |
| [6] | 7. Owens DK (1970) Some thermodynamic aspects of polymer adhesion. J Appl Polym Sci 14(7):1725-1730. |
| [7] | 8. Lee HJ, Michielsen S (2006) Lotus effect: Superhydrophobicity. J Text Inst 95): 455-462. |
| [8] |
9. Cassie ABD, Baxter S (1944) Wettability of porous surfaces. T Faraday Soc 40: 0546-0550. doi: 10.1039/tf9444000546

|
| [9] | 10. Lafuma A, Quere D (2003) Superhydrophobic states. Nat Mater 2(7): 457-460. |
| [10] |
11. Ensikat HJ, Ditsche-Kuru P, Neinhuis C, et al. (2011) Superhydrophobicity in perfection: The outstanding properties of the lotus leaf. Beilstein J Nanotechno 2: 152-161. doi: 10.3762/bjnano.2.19

|
| [11] | 13. Erasmus E, Barkhuysen FA (2009) Superhydrophobic cotton by fluorosilane modification. Indian J Fibre Text 34: 377-379. |
| [12] | 14. Nishino T, Meguro M, Nakamae K, et al. (1999) The lowest surface free energy based on -CF3 alignment. Langmuir 15(13): 4321-4323. |
| [13] | 15. Tada H, Nagayama H (1995) Chemical-vapor surface modification of porous-glass with fluoroalkyl-functionalized silanes 2. resistance to water. Langmuir 11(1): -142. |
| [14] | 16. Thunemann AF (2000) Complexes of polyethyleneimine with perfluorinated carboxylic acids: Wettability of lamellar structured mesophases. Langmuir 16(2): 824-828. |
| [15] | 17. Anton D (1998) Surface-fluorinated coatings. Adv Mater 10(: 1197-1205. |
| [16] | 18. Shibuichi S, Onda T, Satoh N, et al. (1996) Super water-repellent surfaces resulting from fractal structure. J Phys Chem 100(50): 19512-19517. |
| [17] | 19. Shibuichi S, Yamamoto T, Onda T, et al. (1998) Super water- and oil-repellent surfaces resulting from fractal structure. J Colloid Interface Sci 208(1): 287-294. |
| [18] | 20. Onda T, Shibuichi S, Satoh N, et al. (1996) Super-water-repellent fractal surfaces. Langmuir12(9): 2125-2127. |
| [19] | 21. Pasquinelli MA, Yingling YG (2012) Molecular dynamics simulations of bio-nano interactions. In: Encyclopedia of Nanotechnology. Springer 1454-1463. |
| [20] | 22. Lee C, McCammon JA, Rossky PJ (1984) The structure of liquid water at an extended hydrophobic surface. J Chem Phys 80(9): 4448. |
| [21] | 23. Dimitrov DI, Milchev A, Binder K, et al. (2006) Structure of polymer brushes in cylindrical tubes: A molecular dynamics simulation. Macromol Theory Simul 15(7): 573-583. |
| [22] |
24. Dong S, Yan J, Xu N, et al. (2011) Molecular dynamics simulation on surface modification of carbon black with polyvinyl alcohol. Surf Sci 605: 868-874. doi: 10.1016/j.susc.2011.01.021

|
| [23] | 25. Hirvi JT, Pakkanen TA (2007) Wetting of nanogrooved polymer surfaces. Langmuir 14):7724-7729. |
| [24] | 26. Liu H, Li Y, Krause WE, et al. (2012) The soft-confined method for creating molecular models of amorphous polymer surfaces. J Phys Chem B 116(8): 2633. |
| [25] | 27. Bardzinski PJ (2011) Determination of the electronic band structure of the rutile polymorph of TiO2: A quantum chemical approach. Mat Sci-Poland 29(3): 223-232. |
| [26] | 28. Prathab B, Aminabhavi TM (2007) Atomistic simulations to compute surface properties of poly(N-vinyl-2-pyrrolidone) (PVP) and blends of PVP/chitosan. Langmuir 23(10): 5439-5444. |
| [27] | 29. Shi B (2006) Molecular dynamics simulation of the surface tension and contact angle of argon and water [dissertation]. University of California Los Angeles. |
| [28] | 30. Gonzalez-Melchor M (2006) Getting the surface tension from computer simulations. Front Contemp Phys 809: 240-244. |
| [29] | 31. Chauve G, Heux L, Arouini R, et al. (2005) Cellulose poly(ethylene-co-vinyl acetate) nanocomposites studied by molecular modeling and mechanical spectroscopy. Biomacromolecules 6(4): 2025-2031. |
| [30] | 32. Jaffe RL, Gonnet P, Werder T, et al. (2004) Water carbon interactions 2: Calibration of potentials using contact angle data for different interaction models. Mol Simulat 4): 205-216. |
| [31] | 33. Wang J, Kalinichev AG, Kirkpatrick RJ (2006) Effects of substrate structure and composition on the structure, dynamics, and energetics of water at mineral surfaces: A molecular dynamics modeling study. Geochim Cosmochim Ac 70(3): 562-582. |
| [32] | 34. Quddus MAAR, Rojas OJ, Pasquinelli MA (2014) Molecular dynamics simulations of the adhesion of a thin annealed film of oleic acid onto crystalline cellulose. Biomacromolecules15(4): 1476-1483. |
| [33] | 35. Fan C, Cagin T (1995) Wetting of crystalline polymer surfaces-a molecular-dynamics simulation. J Chem Phys 103(20): 9053-9061. |
| [34] | 36. Giovambattista N, Debenedetti PG, Rossky PJ (2007) Effect of surface polarity on water contact angle and interfacial hydration structure. J Phys Chem B 111(32): 9581-9587. |
| [35] | 37. Hirvi JT, Pakkanen TA (2006) Molecular dynamics simulations of water droplets on polymer surfaces. J Chem Phys 125(14): 144712-144712. |
| [36] | 38. Hautman J, Klein M (1991) Microscopic wetting phenomena. Phys Rev Lett 67(13): 1763-1766. |
| [37] | 39. Giovambattista N, Debenedetti PG, Rossky PJ (2007) Effect of surface polarity on water contact angle and interfacial hydration structure. J Phys Chem B 111(32): 9581-9587. |
| [38] | 40. Hong SD, Ha MY, Balachandar S (2009) Static and dynamic contact angles of water droplet on a solid surface using molecular dynamics simulation. J Colloid Interface Sci 339(1): 187-195. |
| [39] | 41. Park J, Ha M, Choi H, et al. (2011) A study on the contact angles of a water droplet on smooth and rough solid surfaces. J Mech Sci Technol 25(2): 323-332. |
| [40] | 42. Sergi D, Scocchi G, Ortona A (2012) Molecular dynamics simulations of the contact angle between water droplets and graphite surfaces. Fluid Phase Equilib 332(0): 173-177. |
| [41] | 43. Ohler B, Langel W (2009) Molecular dynamics simulations on the interface between titanium dioxide and water droplets: A new model for the contact angle. J Phys Chem C 113(23):10189-10197. |
| [42] | 44. Dai Z, Ling J, Huang X et al. (2011) Molecular simulation on the interactions of water with polypropylene surfaces. J Phys Chem C 115(21): 10702-10708. |
| [43] | 45. Heine DR, Grest GS, Webb EB (2005) Surface wetting of liquid nanodroplets: Droplet-size effects. Phys Rev Lett 95(10): 107801. |
| [44] | 46. Scocchi G, Sergi D, D'Angelo C, et al. (2011) Wetting and contact-line effects for spherical and cylindrical droplets on graphene layers: A comparative molecular-dynamics investigation. Phys Rev E 84: 061602. |
| [45] | 47. Mattia D (2007) Templated growth and characterization of carbon nanotubes for nanofluidic applications [dissertation]. Drexel University. |
| [46] | 48. Wu C, Kuo L, Lin S, et al. (2012) Effects of temperature, size of water droplets, and surface roughness on nanowetting properties investigated using molecular dynamics simulation. Comp Mater Sci 53(1): 25-30. |
| [47] | 49. Li H, Zeng XC (2012) Wetting and interfacial properties of water nanodroplets in contact with graphene and monolayer boron nitride sheets. ACS Nano 6(3): 2401-2409. |
| [48] | 50. Chai J, Liu S, Yang X. (2009) Molecular dynamics simulation of wetting on modified amorphous silica surface. Appl Surf Sci 255(22): 9078-9084. |
| [49] | 51. Lee SH, Rossky PJ (1994) A comparison of the structure and dynamics of liquid water at hydrophobic and hydrophilic surfaces—a molecular dynamics simulation study. J Chem Phys100(4): 3334-3345. |
| [50] | 52. Koishi T, Yasuoka K, Fujikawa S, et al. (2011) Measurement of contact-angle hysteresis for droplets on nanopillared surface and in the cassie and wenzel states: A molecular dynamics simulation study. ACS Nano 5(9): 6834-6842. |
| [51] | 53. Shi B, Dhir VK (2009) Molecular dynamics simulation of the contact angle of liquids on solid surfaces. J Chem Phys 130(3): 034705. |
| [52] | 54. Grest G, Heine D, Webb E (2006) Liquid nanodroplets spreading on chemically patterned surfaces. Langmuir 22(10): 4745-4749. |
| [53] | 55. Yu FG, De YS (2010) Molecular-dynamics simulations of droplets on a solid surface. Chinese Phys Lett 27(6): 066802. |
| [54] | 56. Wu H, Borhan A, Fichthorn K (2009) Coarse-grained interaction of a fluid with a physically-patterned solid surface: Application to nanodroplet wetting. J Low Temp Phys157(3-4): 277-295. |
| [55] | 57. Ingebrigtsen T, Toxvaerd S (2007) Contact angles of lennard-jones liquids and droplets on planar surfaces. J Phys Chem C 111(24): 8518-8523. |
| [56] |
58. Leroy F, dos Santos DJVA, Müller-Plathe F (2009) Interfacial excess free energies of solid-liquid interfaces by molecular dynamics simulation and thermodynamic integration. Macromol Rapid Comm 30: 864-870. doi: 10.1002/marc.200800746

|
| [57] | 59. Shahraz A, Borhan A, Fichthorn KA (2013) Wetting on physically patterned solid surfaces: The relevance of molecular dynamics simulations to macroscopic systems. Langmuir 29(37):11632-11639. |
| 1. | S. Mahmood Fatemi, Seyed Jamilaldin Fatemi, Current investigations in theoretical studies of nanostructure–liquid interfaces, 2020, 65, 05779073, 93, 10.1016/j.cjph.2020.02.004 | |
| 2. | Junjun Wang, Tao Li, Yifan Li, Yunrui Duan, Yanyan Jiang, Hamidreza Arandiyan, Hui Li, Wetting Transitions of Liquid Gallium Film on Nanopillar-Decorated Graphene Surfaces, 2018, 23, 1420-3049, 2407, 10.3390/molecules23102407 | |
| 3. | Rita Khanna, 2019, Chapter 1, 978-1-83880-538-8, 10.5772/intechopen.86451 | |
| 4. | Beena Rai, , Modeling self-assembly of surfactants at interfaces, 2017, 15, 22113398, 84, 10.1016/j.coche.2016.12.003 | |
| 5. | Bo Zhang, Yijin Mao, Chung-Lung Chen, Yuwen Zhang, Hybrid atomistic-continuum simulation of nucleate boiling with a domain re-decomposition method, 2017, 71, 1040-7790, 217, 10.1080/10407790.2016.1277916 | |
| 6. | Rahul Bhowmik, Rajiv J. Berry, Michael F. Durstock, Benjamin J. Leever, Prediction of the Wetting Behavior of Active and Hole-Transport Layers for Printed Flexible Electronic Devices Using Molecular Dynamics Simulations, 2017, 9, 1944-8244, 19269, 10.1021/acsami.6b14786 | |
| 7. | Emmanuel M. Gutman, Comment on “Surface elastic constants of a soft solid” by Q. Xu, R. W. Style and E. R. Dufresne, Soft Matter, 2018, 14, 916, 2022, 18, 1744-683X, 4638, 10.1039/D1SM01412A | |
| 8. | Jan Macko, Natalia Podrojková, Renata Oriňaková, Andrej Oriňak, New insights into hydrophobicity at nanostructured surfaces: Experiments and computational models, 2022, 12, 1847-9804, 184798042110623, 10.1177/18479804211062316 | |
| 9. | Sushanta K. Sethi, Sachin Kadian, Gaurav Manik, A Review of Recent Progress in Molecular Dynamics and Coarse-Grain Simulations Assisted Understanding of Wettability, 2022, 29, 1134-3060, 3059, 10.1007/s11831-021-09689-1 | |
| 10. | Ben Hanson, John Hofmann, Melissa A. Pasquinelli, Influence of Copolyester Composition on Adhesion to Soda-Lime Glass via Molecular Dynamics Simulations, 2016, 8, 1944-8244, 13583, 10.1021/acsami.6b01851 | |
| 11. | W. Song, C.Q. Li, L. Lin, Y. Chen, Research on the Mechanical and Thermal Properties of MWCNTs/CF Reinforced Epoxy Resin Matrix Composite Patch, 2013, 50, 18753892, 405, 10.1016/j.phpro.2013.11.062 | |
| 12. | Mikhail S. Polovinkin, Nikolai A. Volkov, Dmitry V. Tatyanenko, Alexander K. Shchekin, Contact angle calculations for argon and water sessile droplets on planar lyophilic and lyophobic surfaces within molecular dynamics modeling, 2024, 09277757, 134932, 10.1016/j.colsurfa.2024.134932 | |
| 13. | A.A. Semenchuk, N.D. Kondratyuk, I.V. Kopanichuk, PANDA: Predicting angle from nanoscale density analysis, 2024, 09277757, 135994, 10.1016/j.colsurfa.2024.135994 |