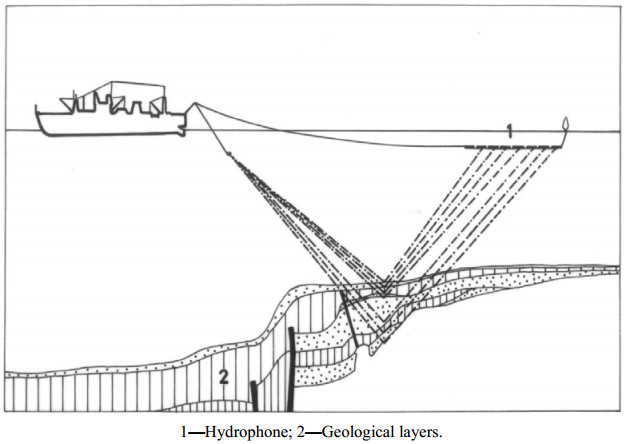
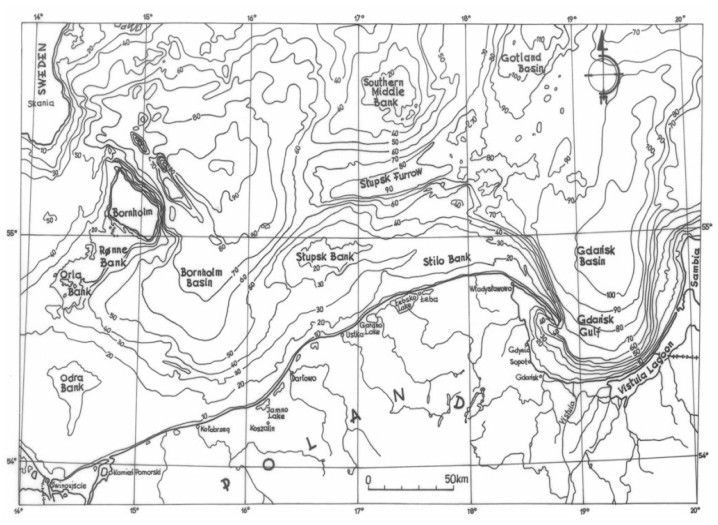
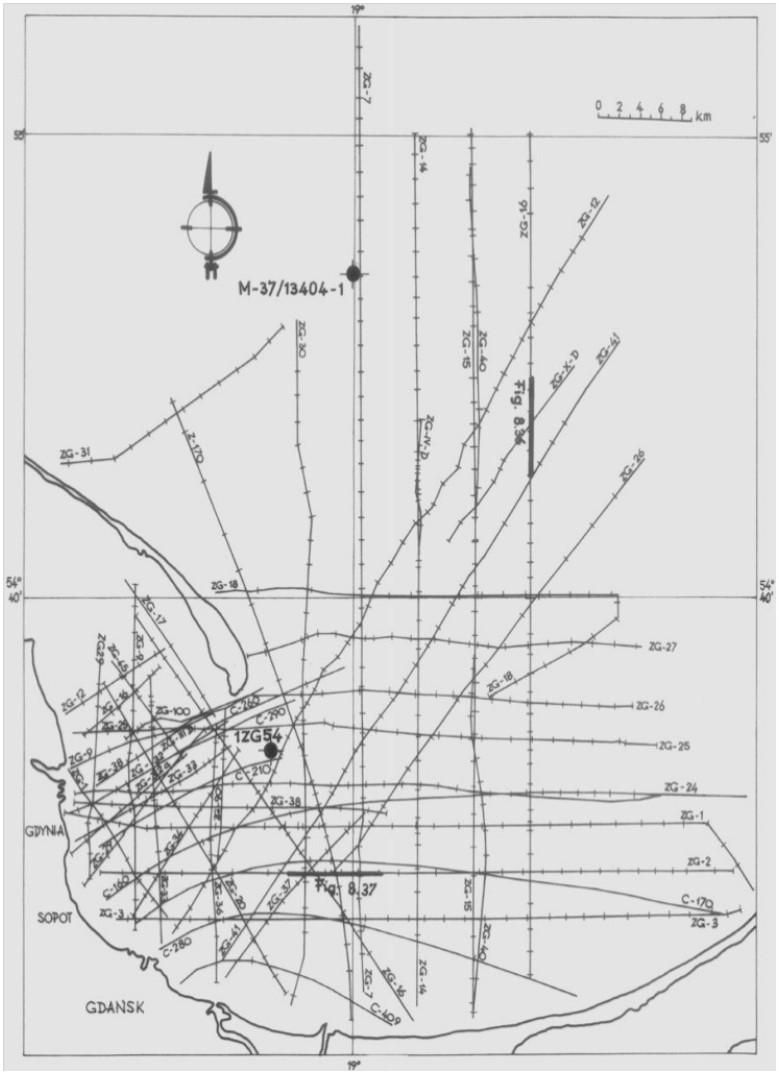
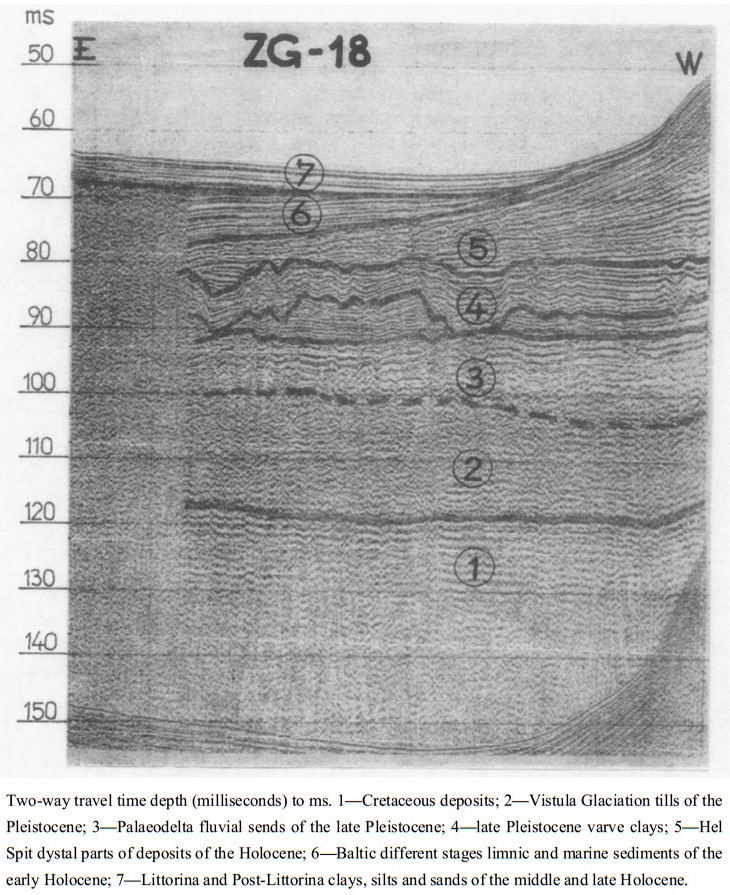
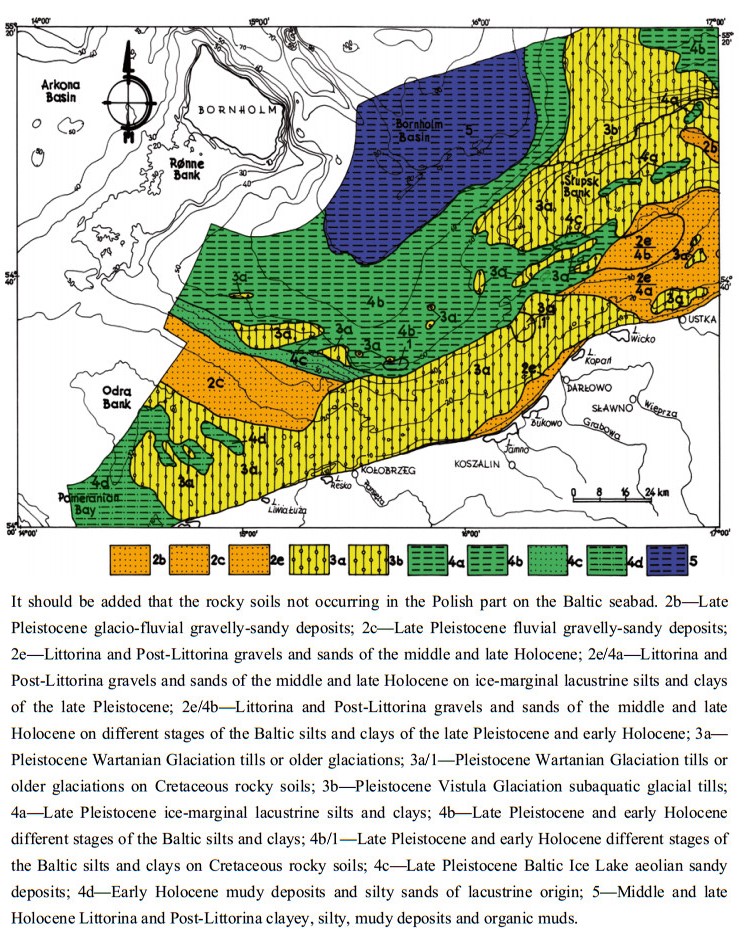
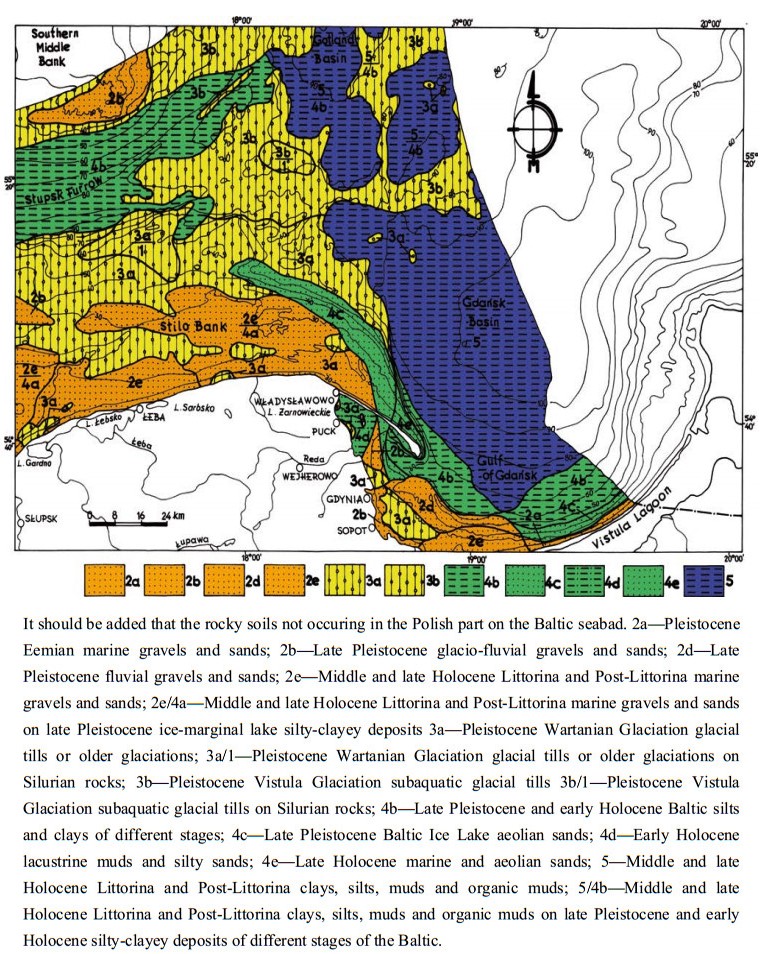
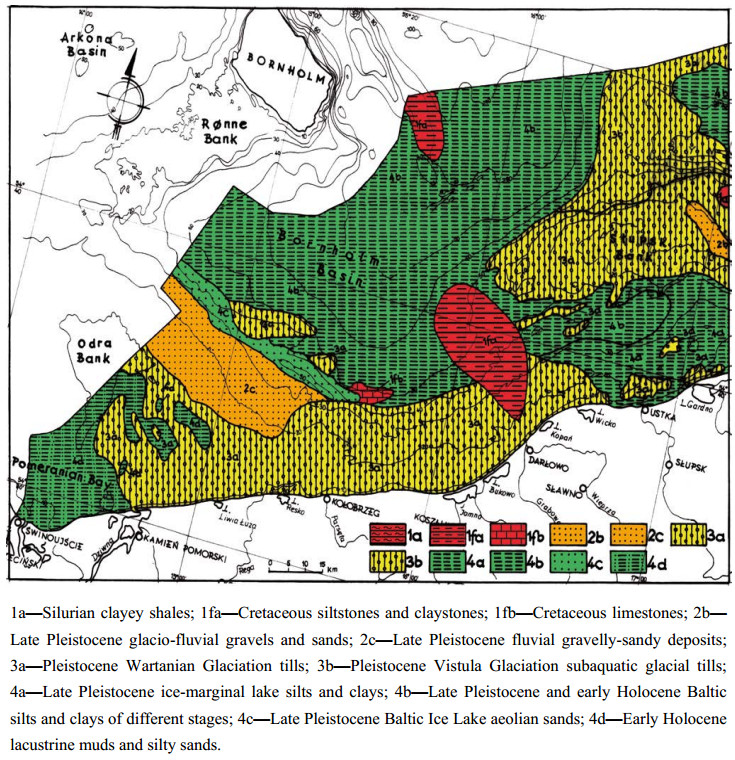
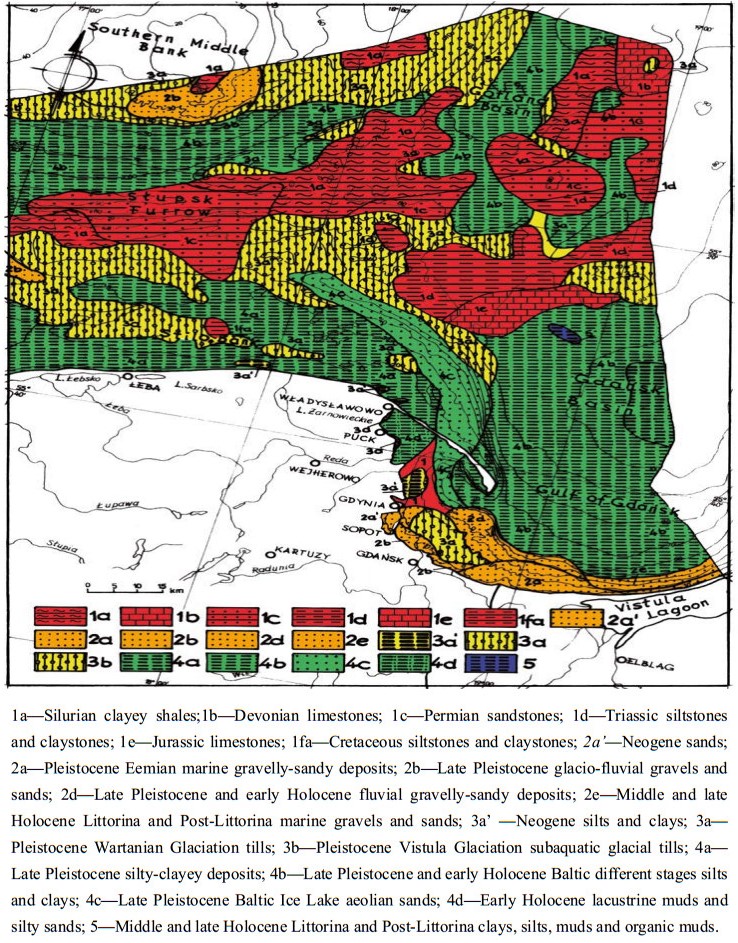
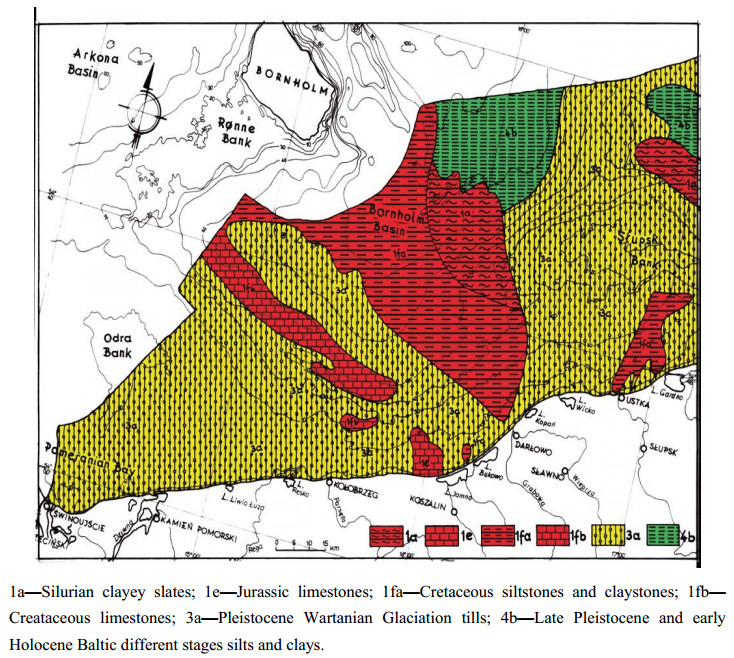
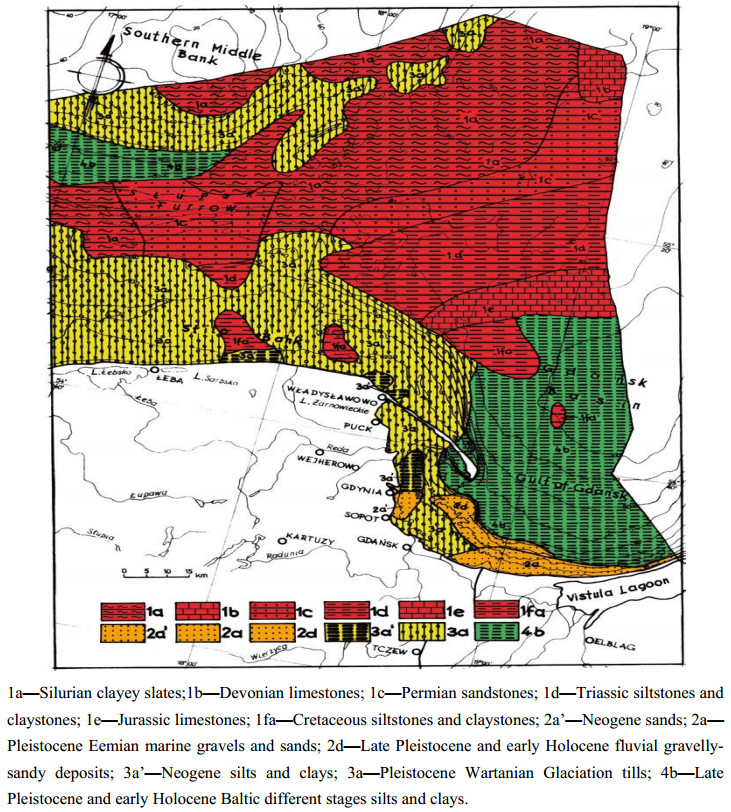
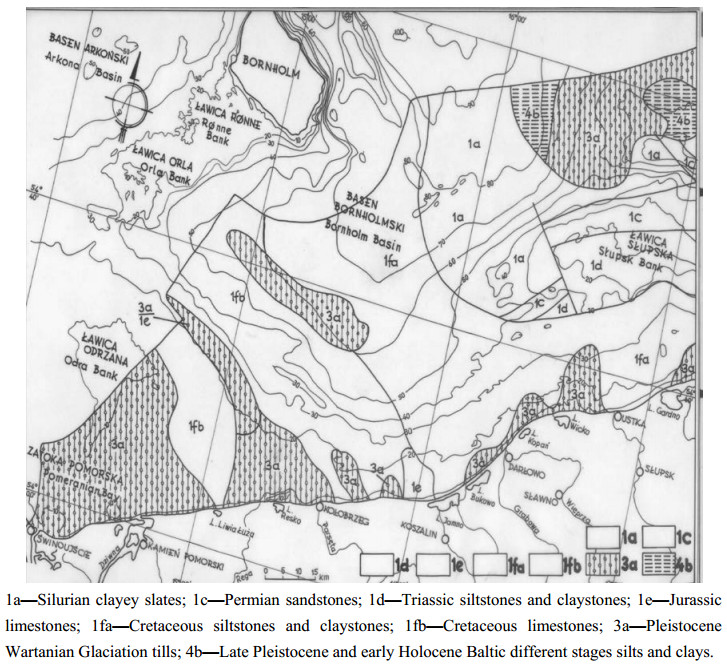
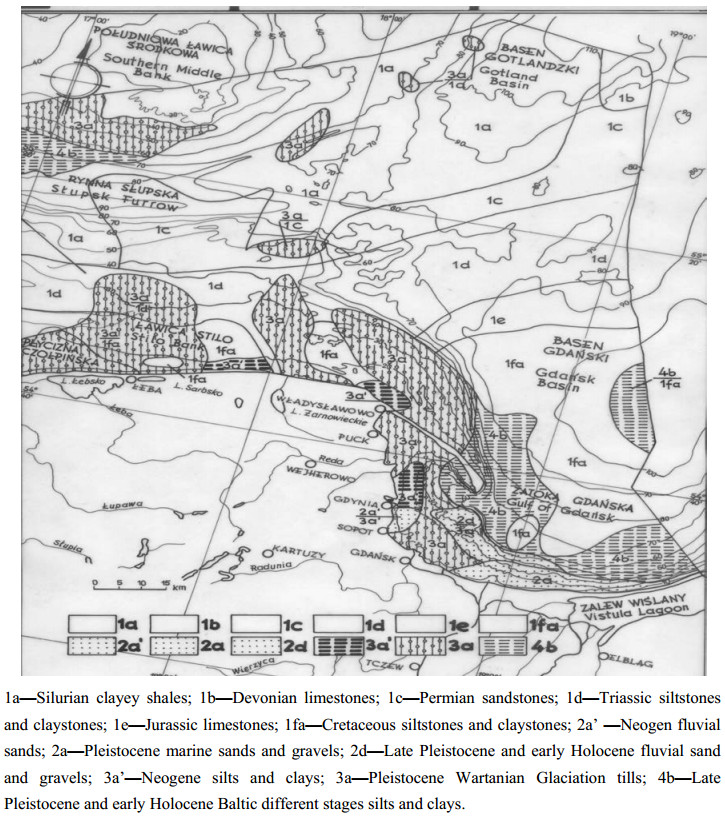
Seismic surveys are widely applied in research on the recognition of geological and geotechnical conditions of seabed and ocean floor sediments. The methodology and equipment needed to carry out shallow seismic and direct geotechnical surveys, as well as the analysis of the results based on the survey of the Polish Baltic Sea bottom, shall be presented here. The interpretation of the seismic survey results is based on the analysis of the registration of different acoustic levels, characteristics of seismo-acoustic layers, their degree of readability and slope angles of individual acoustic reflections. The author deals with the analyses of seismic reflection data and tries to understand the wave image as best as possible. Based on the seismic registrations obtained by the Geofizyka-Toruń company, the author has elaborated interpretation patterns for the Polish Baltic sediments, which are also presented here. The seismic surveys were used to construct maps of specific levels with different geotechnical conditions in the sea-bottom and at a depth of 10, 20 and 30 m below the seabed. The author presents here new results of research related to the geotechnical characteristics of the Polish Baltic substrate at a depth of 30 m below the seabed. The geotechnical map of the Polish Baltic Sea of the substrate at the depth of 30 m below the sea-bottom, as prepared by the author, is very important for building deep foundations of marine constructions, such as oil and gas exploration and production platforms. Seismic surveys allow a good degree of recognition of various geotechnical types of soils in the Polish Baltic sea-bottom, for which approximate values of characteristic geotechnical parameters have been determined.
Abbreviations: H-H inequalities: Hermite-Hadamard inequalities; i-v-ms: Interval-valued mappings; UD order: Up and down order; LR order: Left and Right order; H-H Fejér inequality: Hermite-Hadamard Fejér inequality; IA-integrable: Aumann integrable; FA-integrable: Fuzzy Aumann integrable
1.
Introduction
Numerous academics have been working to generalize and extend the classical convexity in various ways recently, and they have found new integral inequalities for this convexity that has been generalized and extended; for examples, see [1,2,3,4,5,6]. Invex functions, a helpful extension of convex functions, were first presented by Hanson [7] in 1981. The class of invex functions is identical to the class of functions whose stationary points are global minima, as demonstrated by Craven and Glover [8]. Ben-Israel and Mond [9] established the idea of preinvex functions. Preinvex functions are nonconvex functions, as is common knowledge. The study and applications of this newly defined nonconvex function in optimization theory and related domains were the subject of several research articles that were motivated by this idea, see [10,11,12].
Hermite-Hadamard (H-H) inequality, an extension of the traditional H-H inequality, was derived by Noor [13] for the preinvex functions. The idea of classical convex functions on coordinates was developed by Dragomir [14], who also illustrated H-H type inequalities for these functions. Additionally, Latif and Dragomir [15] discovered several H-H type inequalities for functions whose second-order partial derivatives in absolute value are preinvex on the coordinates and defined preinvex functions on the coordinates. Using the symmetry of the positive function, Matoka [16] proposed the class of (h1, h2)-preinvex functions on the coordinates and proved H-H and Fej'er type inequalities. See [17,18,19,20,21] for further information on preinvex functions and associated inequalities.
Moore was the first person to think about interval analysis [22]. Moore [23] conducted research on interval techniques for finding upper and lower limits on the precise values of integrals of interval-valued mappings (i-v-ms) in 1979. He also explored the integration of interval-valued mappings. In order to find effective solutions, Bhurjee and Panda [24] established a generic multi-objective fractional programming problem whose parameters in the objective functions and constraints are intervals. In order to develop KKT optimality requirements for LU-prinvex and invex optimization problems with an interval-valued objective function, Zhang et al. [25] expanded the notions of invexity and preinvexity to interval-valued mappings. For interval-valued mappings, Zhao et al. [26] established the interval double integral and provided Chebyshev type inequalities. Areas of economics, chemical engineering, beam physics, control circuitry design, global optimization, robotics, error analysis, signal processing, and computer graphics are among the practical uses of interval analysis (see [27,28,29,30,31]).
Remember that fuzzy interval-valued functions are fuzzy number valued mappings. On the other hand, Nanda and Kar [32] were the first to introduce the idea of convex fuzzy number valued mappings. In order to offer new versions of H-H and fractional type of inequalities, Khan et al. [33,34] presented h-convex fuzzy number valued mappings and (h1, h 2)-convex fuzzy number valued functions and got some by utilizing fuzzy Riemann Liouville Fractional Integrals and fuzzy Riemannian integrals, respectively. Similarly, using fuzzy order relations and fuzzy Riemann Liouville Fractional Integrals, Sana and Khan et al. [35] developed new iterations of fuzzy fractional H-H inequalities for harmonically convex fuzzy number valued mappings. We direct the readers to [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67] and the references therein for further information on extended convex functions, fuzzy intervals, and fuzzy integrals.
Zhao et al. [5,26] and Zhang et al. [49] serve as major sources of inspiration for the work in this study report. As an extension of classical convex functions, we introduce the concept of up and down λ-convex fuzzy-number valued mapping via up and down fuzzy relation and provide new H-H type fuzzy inclusions for these functions. For the result of two up and down λ-convex fuzzy-number valued mappings, we additionally give H-H type fuzzy inclusions. Moreover, we use some appropriate cases to highlight our findings. As a specific situation, the results for up and down λ-convex fuzzy-number valued mapping are included in the conclusions drawn in this study. Using fuzzy Riemann integrals, we can look at H-H type inclusions for up and down λ-convex fuzzy-number valued mapping that have fuzzy number values.
The following is how this paper is organized: We provide a few important introductions in Section 2. Moreover, Section 2 also provides the definition of up and down λ-convex fuzzy-number valued mapping and some related basic concepts. Section 3 provides an analysis of H-H type fuzzy inclusions. In addition, we provide H-H type fuzzy inclusions for the product of two up and down λ-convex fuzzy-number valued mappings. Moreover, we have proved the weighted H-H type fuzzy inclusions for up and down λ-convex fuzzy-number valued mapping. In Section 3, certain unique instances of these results are also examined. We examine the study's findings and potential directions in Section 4.
2.
Preliminaries
Let XI be the space of all closed and bounded intervals of R and w∈XI be defined by
If w∗=w∗, then w is said to be degenerate. In this article, all intervals will be non-degenerate intervals. If w∗≥0, then [w∗,w∗] is called a positive interval. The set of all positive intervals is denoted by X+I and defined as X+I={[w∗,w∗]:[w∗,w∗]∈XIandw∗≥0}.
Let ς∈R and ς⋅w be defined by
Then the Minkowski difference x−w, addition w+x and w×x for w,x∈XI are defined by
Remark 1. (ⅰ) For given [x∗,x∗],[w∗,w∗]∈XI, the relation "⊇I" defined on XI by
for all [x∗,x∗],[w∗,w∗]∈XI, it is a partial interval inclusion relation. The relation [w∗,w∗]⊇I[x∗,x∗] coincident to [w∗,w∗]⊇[x∗,x∗] on XI. It can be easily seen that "⊇I" looks like "up and down" on the real line R, so we call "⊇I" is "up and down" (or "UD" order, in short) [49].
(ⅱ) For given [x∗,x∗],[w∗,w∗]∈XI, we say that [x∗,x∗]≤I[w∗,w∗] if and only if x∗≤w∗,x∗≤w∗ or x∗≤w∗,x∗<w∗, it is an partial interval order relation. The relation [x∗,x∗]≤I[w∗,w∗] coincident to [x∗,x∗]≤[w∗,w∗] on XI. It can be easily seen that "≤I" looks like "left and right" on the real line R, so we call "≤I" is "left and right" (or "LR" order, in short) [48,49].
For [x∗,x∗],[w∗,w∗]∈XI, the Hausdorff-Pompeiu distance between intervals [x∗,x∗] and [w∗,w∗] is defined by
It is familiar fact that (XI,dH) is a complete metric space [40,46,47].
Definition 1. [39,40] A fuzzy subset L of R is distinguished by a mapping ˜w:R→[0,1] called the membership mapping of L. That is, a fuzzy subset L of R is a mapping ˜w:R→[0,1]. So for further study we have choosed this notation. We appoint E to denote the set of all fuzzy subsets of R.
Definition 2. [39,40] Given ˜w∈EC, the level sets or cut sets are given by [˜w]i={ϰ∈R|˜w(ϰ)>i} for all i∈[0,1] and by [˜w]0={ϰ∈R|˜w(ϰ)>0}. These sets are known as i-level sets or i-cut sets of ˜w.
Definition 3. [41] Let ˜w∈E. Then, ˜w is known as fuzzy number or fuzzy number if following properties are satisfied by ˜w:
(1) ˜w should be normal if there exists ϰ∈R and ˜w(ϰ)=1;
(2) ˜w should be upper semi continuous on R if for given ϰ∈R, there exist ϵ>0 there exist δ>0 such that ˜w(ϰ)−˜w(s)<ϵ for all ϰ,s∈R with |ϰ−s|<δ;
(3) ˜w should be fuzzy convex that is ˜w((1−ς)ϰ+ςs)≥min(˜w(ϰ),˜w(s)), for all ϰ,s∈R and ς∈[0,1];
(4) ˜w should be compactly supported that is cl{ς∈R|˜w(ϰ)>0} is compact.
We appoint EC to denote the set of all fuzzy numbers of R.
Proposition 1. [42] Let ˜w,˜x∈EC. Then relation "≤F" given on EC by
it is left and right order relation.
Proposition 2. [57] Let ˜w,˜x∈EC. Then relation "⊇F" given on EC by
it is up and down order relation on EC.
Remember the approaching notions, which are offered in literature. If ˜w,˜x∈EC and i∈R, then, for every i∈[0,1], the arithmetic operations are defined by
These operations follow directly from the Eqs. (2)–(4), respectively.
Theorem 1. [40] The space EC dealing with a supremum metric i.e., for ˜w,˜x∈EC
is a complete metric space, where H denote the well-known Hausdorff metric on space of intervals.
2.1. Riemann integral operators for interval and fuzzy-number valued mappings
Now we define and discuss some properties fractional integral operators of interval and fuzzy-number valued mappings.
Theorem 2. [40,41] If Υ:[τ,ϑ]⊂R→XI is an interval-valued mapping (i-v-m) satisfying that Υ(ϰ)=[Υ∗(ϰ),Υ∗(ϰ)], then Υ is Aumann integrable (IA-integrable) over [τ,ϑ] if and only if, Υ∗(ϰ) and Υ∗(ϰ) both are integrable over [τ,ϑ] such that
Definition 4. [48] Let ˜Υ:I⊂R→EC is called fuzzy-number valued mapping. Then, for every i∈[0,1], as well as i-levels define the family of i-v-ms Υi:I⊂R→XI satisfying that Υi(ϰ)=[Υ∗(ϰ,i),Υ∗(ϰ,i)] for every ϰ∈I. Here, for every i∈[0,1], the endpoint real-valued mappings Υ∗(∙,i),Υ∗(∙,i):I→R are called lower and upper mappings of Υ.
Definition 5. [48] Let ˜Υ:I⊂R→EC be a fuzzy-number valued mapping. Then ˜Υ(ϰ) is said to be continuous at ϰ∈I, if for every i∈[0,1], Υi(ϰ) is continuous if and only if, both endpoint mappings Υ∗(ϰ,i) and Υ∗(ϰ,i) are continuous at ϰ∈I.
Definition 6. [41] Let ˜Υ:[τ,ϑ]⊂R→EC is fuzzy-number valued mapping. The fuzzy Aumann integral ((FA)-integral) of ˜Υ over [τ,ϑ], denoted by (FA)∫ϑτ˜Υ(ϰ)dϰ, is defined level-wise by
where S(Υi)={Υ(.,i)→R:Υ(.,i)isintegrableandΥ(ϰ,i)∈Υi(ϰ)}, for every i∈[0,1]. ˜Υ is (FA)-integrable over [τ,ϑ] if (FA)∫ϑτ˜Υ(ϰ)dϰ∈EC.
Theorem 3. [42] Let ˜Υ:[τ,ϑ]⊂R→EC be a fuzzy-number valued mapping, as well as i-levels, define the family of i-v-ms Υi:[τ,ϑ]⊂R→XI satisfying that Υi(ϰ)=[Υ∗(ϰ,i),Υ∗(ϰ,i)] for every ϰ∈[τ,ϑ] and for every i∈[0,1]. Then ˜Υ is (FA)-integrable over [τ,ϑ] if and only if, Υ∗(ϰ,i) and Υ∗(ϰ,i) both are integrable over [τ,ϑ]. Moreover, if ˜Υ is (FA)-integrable over [τ,ϑ], then
for every i∈[0,1].
The family of all (FA)-integrable fuzzy-number valued mappings over [τ,ϑ] are denoted by FA([τ,ϑ],i).
Breckner discussed the coming emerging idea of interval-valued convexity in [43].
A i-v-m Υ:I=[τ,ϑ]→XI is called convex i-v-m if
for all ϰ,y∈[τ,ϑ],ς∈[0,1], where XI is the collection of all real valued intervals. If (17) is reversed, then Υ is called concave.
Definition 7. [32] The fuzzy-number valued mapping Υ:[τ,ϑ]→EC is called convex fuzzy-number valued mapping on [τ,ϑ] if
for all ϰ,s∈[τ,ϑ],ς∈[0,1], where ˜Υ(ϰ)≥F˜0 for all ϰ∈[τ,ϑ]. If (18) is reversed then, ˜Υ is called concave fuzzy-number valued mapping on [τ,ϑ]. ˜Υ is affine if and only if it is both convex and concave fuzzy-number valued mapping.
Definition 8. [49] The fuzzy-number valued mapping ˜Υ:[τ,ϑ]→EC is called up and down convex fuzzy-number valued mapping on [τ,ϑ] if
for all ϰ,s∈[τ,ϑ],ς∈[0,1], where ˜Υ(ϰ)≥F˜0 for all ϰ∈[τ,ϑ]. If (19) is reversed then, ˜Υ is called up and down concave fuzzy-number valued mapping on [τ,ϑ]. ˜Υ is up and down affine fuzzy-number valued mapping if and only if it is both up and down convex and, up and down concave fuzzy-number valued mapping.
Definition 9. [62] Let K be convex set and λ:[0,1]⊆K→R+ such that λ≢0. Then fuzzy-number valued mapping ˜Υ:K→EC is said to be up and down λ-convex on K if
for all ϰ,s∈K,ς∈[0,1], where ˜Υ(ϰ)≽˜0. The fuzzy-number valued mapping ˜Υ:K→EC is said to be up and down λ-concave on K if inequality (20) is reversed. Moreover, ˜Υ is known as affine up and down λ-convex fuzzy-number valued mapping on K if
for all ϰ,s∈K,ς∈[0,1], where ˜Υ(ϰ)≽˜0.
Remark 2. The up and down λ-convex fuzzy-number valued mappings have some very nice properties similar to convex fuzzy-number valued mapping,
1) if ˜Υ is up and down λ-convex fuzzy-number valued mapping, then α˜Υ is also up and down λ-convex for α≥0.
2) if ˜Υ and ˜T both are up and down λ-convex fuzzy-number valued mappings, then max(˜Υ(ϰ),˜T(ϰ)) is also up and down λ-convex fuzzy-number valued mapping.
Here, we will go through a few unique exceptional cases of up- and down-convex fuzzy-number valued mappings:
(ⅰ) If λ(ς)=ςs, then up and down λ-convex fuzzy-number valued mapping becomes up and down s-convex fuzzy-number valued mapping, that is
(ⅱ) If λ(ς)=ς, then up and down λ-convex fuzzy-number valued mapping becomes up and down convex fuzzy-number valued mapping, see [49], that is
(ⅲ) If λ(ς)≡1, then up and down λ-convex fuzzy-number valued mapping becomes up and down P-convex fuzzy-number valued mapping, that is
Note that, there are also new special cases (ⅰ) and (ⅲ) as well.
Theorem 4. [62] Let K be convex set, non-negative real valued function λ:[0,1]⊆K→R such that λ≢0 and let ˜Υ:K→EC be a fuzzy-number valued mapping, whose i-levels define the family of i-v-ms Υi:K⊂R→X+I⊂XI are given by
for all ϰ∈K and for all i∈[0,1]. Then ˜Υ is up and down λ-convex on K, if and only if, for all i∈[0,1], Υ∗(ϰ,i) is λ-convex and Υ∗(ϰ,i) is λ-concave.
Remark 3. If Υ∗(ϰ,i)=Υ∗(ϰ,i) with i=1, then up and down λ-convex fuzzy number valued function reduces to the λ-convex function.
If Υ∗(ϰ,i)=Υ∗(ϰ,i) with i=1 and λ(ς)=ςs with s∈(0,1), then up and down λ-convex fuzzy number valued function reduces to the s-convex function.
If Υ∗(ϰ,i)=Υ∗(ϰ,i) with i=1 and λ(ς)=ς with s∈(0,1), then up and down λ-convex fuzzy number valued function reduces to the convex function.
If Υ∗(ϰ,i)=Υ∗(ϰ,i) with i=1 and λ(ς)=1, then up and down λ-convex fuzzy number valued function reduces to the P-convex function.
Example 1. We consider λ(ς)=ς, for ς∈[0,1] and the fuzzy-number valued mapping ˜Υ:[0,1]→EC defined by
Then, for each i∈[0,1], we have Υi(ϰ)=[2iϰ2,(4−2i)ϰ2]. Since end point functions Υ∗(ϰ,i), Υ∗(ϰ,i) are λ-convex and λ-concave functions for each i∈[0,1], respectively. Hence ˜Υ(ϰ) is up and down λ-convex fuzzy-number valued mapping.
Definition 10. [62] Let ˜Υ:[τ,ϑ]→EC be a fuzzy-number valued mapping, whose i-levels define the family of i-v-ms Υi:[τ,ϑ]→X+C⊂XC are given by
for all \boldsymbol{\varkappa }\in [\boldsymbol{\tau }, \boldsymbol{\vartheta }] and for all \mathcal{i}\in \left[ {{\bf{0}},{\bf{1}}} \right] . Then, \widetilde {{{\boldsymbol{\varUpsilon }}}} is lower up and down \boldsymbol{\lambda } -convex ( \boldsymbol{\lambda } -concave) fuzzy-number valued mapping on [\boldsymbol{\tau }, \boldsymbol{\vartheta }], if and only if, for all \mathcal{i}\in \left[ {{\bf{0}},{\bf{1}}} \right], {{{\boldsymbol{\varUpsilon }}}}_{\mathit{*}}\left(\boldsymbol{\varkappa }, \mathcal{i}\right) is a \boldsymbol{\lambda } -convex ( \boldsymbol{\lambda } -concave) mapping and {{{\boldsymbol{\varUpsilon }}}}^{\mathit{*}}\left(\boldsymbol{\varkappa }, \boldsymbol{\lambda }\right) is a \boldsymbol{\lambda } -affine mapping.
Definition 11. [62] Let \widetilde {\mathit{\Upsilon }}:[\tau, \vartheta]\to {\mathbb{E}}_{C} be a fuzzy-number valued mapping, whose \mathcal{i} -levels define the family of i-v-ms {\mathit{\Upsilon }}_{\mathcal{i}}:[\tau, \vartheta]\to {\mathcal{X}}_{C}^{+}\subset {\mathcal{X}}_{C} are given by
for all \boldsymbol{\varkappa }\in [\boldsymbol{\tau }, \boldsymbol{\vartheta }] and for all \mathcal{i}\in \left[ {{\bf{0}},{\bf{1}}} \right] . Then, \widetilde {{{\boldsymbol{\varUpsilon }}}} is an upper up and down \boldsymbol{\lambda } -convex ( \boldsymbol{\lambda } -concave) fuzzy-number valued mapping on [\boldsymbol{\tau }, \boldsymbol{\vartheta }], if and only if, for all \mathcal{i}\in \left[ {{\bf{0}},{\bf{1}}} \right], {{{\boldsymbol{\varUpsilon }}}}_{\mathit{*}}\left(\boldsymbol{\varkappa }, \mathcal{i}\right) is an \boldsymbol{\lambda } -affine mapping and {{{\boldsymbol{\varUpsilon }}}}^{\mathit{*}}\left(\boldsymbol{\varkappa }, \mathcal{i}\right) is a \boldsymbol{\lambda } -convex ( \boldsymbol{\lambda } -concave) mapping.
Remark 4. If \boldsymbol{\lambda }\left(\mathit{\varsigma }\right) = \mathit{\varsigma } , then both concepts "up and down \boldsymbol{\lambda } -convex fuzzy-number valued mapping" and classical "convex fuzzy-number valued mapping, see [32]" behave alike when \widetilde {{\boldsymbol{\varUpsilon }}} is lower up and down convex fuzzy-number valued mapping.
Both concepts "convex interval-valued mapping, see [43]" and "left and right \lambda -convex interval-valued mapping, see [49]" are coincident when {\mathit{\Upsilon }} is lower up and down \lambda -convex fuzzy-number valued mapping with \mathcal{i} = 1 .
3.
Main results
The fuzzy Hermite-Hadamard inequalities for up and down \lambda -convex fuzzy-number valued mappings are established in this section. Additionally, several instances are provided to support the theory produced in this study's application.
Theorem 5. Let \widetilde {\mathit{\Upsilon }}:\left[\tau, \vartheta \right]\to {\mathbb{E}}_{C} be an up and down \lambda -convex fuzzy-number valued mapping with non-negative real valued function \lambda :[0, 1]\to {\mathbb{R}}^{+} and \lambda \left(\frac{1}{2}\right)\ne 0 , whose \mathcal{i} -levels define the family of i-v-ms {\mathit{\Upsilon }}_{\mathcal{i}}:\left[\tau, \vartheta \right]\subset \mathbb{R}\to {\mathcal{X}}_{I}^{+} are given by {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[{\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right), {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right)\right] for all \varkappa \in \left[\tau, \vartheta \right] and for all \mathcal{i}\in \left[0, 1\right] . If \widetilde {\mathit{\Upsilon }}\in {\mathcal{F}\mathcal{A}}_{\left(\left[\tau, \vartheta \right], \mathcal{i}\right)} , then
If \widetilde {\mathit{\Upsilon }} is up and down \lambda -concave fuzzy-number valued mapping, then (25) is reversed.
Proof. Let \widetilde {\mathit{\Upsilon }}:\left[\tau, \vartheta \right]\to {\mathbb{E}}_{C} be an up and down \lambda -convex fuzzy-number valued mapping. Then, for a, b\in \left[\tau, \vartheta \right] , we have
If \varsigma = \frac{1}{2} , then we have
Let a = \varsigma \tau +\left(1-\varsigma \right)\vartheta and b = \left(1-\varsigma \right)\tau +\varsigma \vartheta . Then, above inequality we have
Therefore, for every \mathcal{i}\in [0, 1] , we have
Then
It follows that
That is
Thus,
In a similar way as above, we have
Combining (27) and (28), we have
Hence, the required result.
Note that, by using same steps, the formula (26) can be proved with the help of up and down \lambda -concave fuzzy-number valued mapping.
Remark 5. If \lambda \left(\varsigma \right) = {\varsigma }^{s} , then Theorem 5 reduces to the result for up and down s -convex fuzzy-number valued mapping which is also new one:
If \lambda \left(\varsigma \right) = \varsigma , then Theorem 5 reduces to the result for up and down convex fuzzy-number valued mapping which is also new one:
If \lambda \left(\varsigma \right)\equiv 1 then Theorem 5 reduces to the result for up and down P -convex fuzzy-number valued mapping which is also new one:
If {\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right) = {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right) with \mathcal{i} = 1 , then Theorem 5 reduces to the result for classical \lambda -convex function, see [5]:
If {\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right)\ne {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right) with \mathcal{i} = 1 and \lambda \left(\varsigma \right) = \varsigma , then Theorem 5 reduces to the result for classical convex function, see [5]:
If {\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right) = {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right) with \mathcal{i} = 1 , then Theorem 5 reduces to the result for classical \lambda -convex function, see [64]:
If {\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right) = {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right) with \mathcal{i} = 1 and \lambda \left(\varsigma \right) = {\varsigma }^{s} , then Theorem 5 reduces to the result for classical s -convex function, see [64]:
If {\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right) = {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right) with \mathcal{i} = 1 and \lambda \left(\varsigma \right) = \varsigma , then Theorem 5 reduces to the result for classical convex function:
If {\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right) = {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right) with \mathcal{i} = 1 and \lambda \left(\varsigma \right)\equiv 1 then Theorem 5 reduces to the result for classical P -convex function:
Example 2. We consider \lambda \left(\varsigma \right) = \varsigma, for \varsigma \in \left[0, 1\right] , and the fuzzy-number valued mapping \widetilde {\mathit{\Upsilon }}:\left[\tau, \vartheta \right] = [2, 3]\to {\mathbb{E}}_{C} defined by,
Then, for each \mathcal{i}\in \left[0, \mathrm{ }1\right], we have {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[\left(1-\mathcal{i}\right)\left(2-{\varkappa }^{\frac{1}{2}}\right)+3\mathcal{i}, \left(1-\mathcal{i}\right)\left(2+{\varkappa }^{\frac{1}{2}}\right)+3\mathcal{i}\right] . Since left and right end point mappings {\mathit{\Upsilon }}_{\mathrm{*}}\left(\varkappa, \mathcal{i}\right) = \left(1-\mathcal{i}\right)\left(2-{\varkappa }^{\frac{1}{2}}\right)+3\mathcal{i}, {\mathit{\Upsilon }}^{\mathrm{*}}\left(\varkappa, \mathcal{i}\right) = \left(1-\mathcal{i}\right)\left(2+{\varkappa }^{\frac{1}{2}}\right)+3\mathcal{i} , are convex mappings for each \mathcal{i}\in [0, \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }1] , then \widetilde {\mathit{\Upsilon }}\left(\varkappa \right) is up and down convex fuzzy-number valued mapping. We clearly see that {\mathit{\Upsilon }}\in L\left(\left[\tau, \vartheta \right], {\mathbb{E}}_{C}\right) . Now computing the following
for all \mathcal{i}\in \left[0, 1\right]. That means
Similarly, it can be easily show that
for all \mathcal{i}\in \left[0, 1\right], such that
From which, we have
that is
for all \mathcal{i}\in \left[0, 1\right].
Hence,
Theorem 6. Let \widetilde {\mathit{\Upsilon }}:\left[\tau, \vartheta \right]\to {\mathbb{E}}_{C} be an up and down \lambda -convex fuzzy-number valued mapping with non-negative real valued function \lambda :[0, 1]\to {\mathbb{R}}^{+} and \lambda \left(\frac{1}{2}\right)\ne 0, whose \mathcal{i} -levels define the family of i-v-ms {\mathit{\Upsilon }}_{\mathcal{i}}:\left[\tau, \vartheta \right]\subset \mathbb{R}\to {\mathcal{X}}_{I}^{+} are given by {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[{\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right), {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right)\right] for all \varkappa \in \left[\tau, \vartheta \right] and for all \mathcal{i}\in \left[0, 1\right] . If \widetilde {\mathit{\Upsilon }}\in {\mathcal{F}\mathcal{A}}_{\left(\left[\tau, \vartheta \right], \mathcal{i}\right)} , then
where
and {⪧}_{1} = \left[{{⪧}_{1}}_{*}, {{⪧}_{1}}^{*}\right] , {⪧}_{2} = \left[{{⪧}_{2}}_{*}, {{⪧}_{2}}^{*}\right].
Proof. Take \left[\tau, \frac{\tau +\vartheta }{2}\right], we have
Therefore, for every \mathcal{i}\in [0, 1] , we have
In consequence, we obtain
That is
It follows that
In a similar way as above, we have
Combining (39) and (40), we have
By using Theorem 5, we have
Therefore, for every \mathcal{i}\in [0, 1] , we have
that is
hence, the result follows.
Example 3. We consider \lambda \left(\varsigma \right) = \varsigma, for \varsigma \in \left[0, 1\right] , and the fuzzy-number valued mapping \widetilde {\mathit{\Upsilon }}:\left[\tau, \vartheta \right] = [2, 3]\to {\mathbb{E}}_{C} defined by, {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[\left(1-\mathcal{i}\right)\left(2-{\varkappa }^{\frac{1}{2}}\right)+3\mathcal{i}, \left(1-\mathcal{i}\right)\left(2+{\varkappa }^{\frac{1}{2}}\right)+3\mathcal{i}\right], as in Example 2, then \widetilde {\mathit{\Upsilon }}\left(\varkappa \right) is \lambda -convex fuzzy-number valued mapping and satisfying (25). We have {\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right) = \left(1-\mathcal{i}\right)\left(2-{\varkappa }^{\frac{1}{2}}\right)+3\mathcal{i} and {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right) = \left(1-\mathcal{i}\right)\left(2+{\varkappa }^{\frac{1}{2}}\right)+3\mathcal{i} . We now compute the following:
Then we obtain that
Hence, Theorem 6 is verified.
The novel fuzzy Hermite-Hadamard inequalities for the product of two up and down \lambda -convex fuzzy-number valued mappings are found in the results.
Theorem 7. Let \widetilde {\mathit{\Upsilon }}, \widetilde {\mathcal{J}}:\left[\tau, \vartheta \right]\to {\mathbb{E}}_{C} be two up and down \lambda -convex fuzzy-number valued mappings with non-negative real valued functions {\lambda }_{1}, {\lambda }_{2}:[0, 1]\to {\mathbb{R}}^{+} and {\lambda }_{1}\left(\frac{1}{2}\right){\lambda }_{2}\left(\frac{1}{2}\right)\ne 0, whose \mathcal{i} -levels define the family of i-v-ms {\mathit{\Upsilon }}_{\mathcal{i}}, {\mathcal{J}}_{\mathcal{i}}:\left[\tau, \vartheta \right]\subset \mathbb{R}\to {\mathcal{X}}_{I}^{+} are given by {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[{\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right), {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right)\right] and {\mathcal{J}}_{\mathcal{i}}\left(\varkappa \right) = \left[{\mathcal{J}}_{\mathcal{*}}\left(\varkappa, \mathcal{i}\right), {\mathcal{J}}^{\mathcal{*}}\left(\varkappa, \mathcal{i}\right)\right] for all \varkappa \in \left[\tau, \vartheta \right] and for all \mathcal{i}\in \left[0, 1\right] . If \widetilde {\mathit{\Upsilon }}, \widetilde {\mathcal{J}} and \widetilde {\mathit{\Upsilon }}\otimes \widetilde {\mathcal{J}}\in {\mathcal{F}\mathcal{A}}_{\left(\left[\tau, \vartheta \right], \mathcal{i}\right)} , then
where \widetilde {\mathcal{M}}\left(\tau, \vartheta \right) = \widetilde {\mathit{\Upsilon }}\left(\tau \right)\otimes \widetilde {\mathcal{J}}\left(\tau \right) \oplus \widetilde {\mathit{\Upsilon }}\left(\vartheta \right)\otimes \widetilde {\mathcal{J}}\left(\vartheta \right), \widetilde {\mathcal{N}}\left(\tau, \vartheta \right) = \widetilde {\mathit{\Upsilon }}\left(\tau \right)\otimes \widetilde {\mathcal{J}}\left(\vartheta \right) \oplus \widetilde {\mathit{\Upsilon }}\left(\vartheta \right)\otimes \widetilde {\mathcal{J}}\left(\tau \right), and {\mathcal{M}}_{\mathcal{i}}\left(\tau, \vartheta \right) = \left[{\mathcal{M}}_{\mathcal{*}}\left(\left(\tau, \vartheta \right), \mathcal{i}\right), {\mathcal{M}}^{\mathcal{*}}\left(\left(\tau, \vartheta \right), \mathcal{i}\right)\right] and {\mathcal{N}}_{\mathcal{i}}\left(\tau, \vartheta \right) = \left[{\mathcal{N}}_{\mathcal{*}}\left(\left(\tau, \vartheta \right), \mathcal{i}\right), {\mathcal{N}}^{\mathcal{*}}\left(\left(\tau, \vartheta \right), \mathcal{i}\right)\right].
Proof. Let \widetilde {\mathit{\Upsilon }}, \widetilde {\mathcal{J}}:\left[\tau, \vartheta \right]\to {\mathbb{E}}_{C} be two up and down {\lambda }_{1} -convex and {\lambda }_{2} -convex fuzzy-number valued mappings. Then, we have
And
From the definition of up and down \lambda -convex fuzzy number valued mapping it follows that \widetilde {\mathit{\Upsilon }}\left(x\right){\begin{array}{c}\begin{array}{c}\ge \end{array}\end{array}}_{\mathbb{F}}0 and \widetilde {\mathcal{J}}\left(x\right){\begin{array}{c}\begin{array}{c}\ge \end{array}\end{array}}_{\mathbb{F}}0 , so
Integrating both sides of above inequality over [0, 1] we get
It follows that,
that is
Thus,
and the theorem has been established.
Example 4. We consider {\lambda }_{1}\left(\varsigma \right) = \varsigma, {\lambda }_{2}\left(\varsigma \right) = \varsigma, for \varsigma \in \left[0, 1\right] , and the fuzzy-number valued mappings \widetilde {\mathit{\Upsilon }}, \widetilde {\mathcal{J}}:\left[\tau, \vartheta \right] = [0, 2]\to {\mathbb{E}}_{C} defined by,
Then, for each \mathcal{i}\in \left[0, \mathrm{ }1\right], we have {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[\mathcal{i}\varkappa, (2-\mathcal{i})\varkappa \right] and {\mathcal{J}}_{\mathcal{i}}\left(\varkappa \right) = \left[\left(1-\mathcal{i}\right)\varkappa +2\mathcal{i}, \left(1-\mathcal{i}\right)\left(8-{e}^{\varkappa }\right)+2\mathcal{i}\right]. Since end point functions {\mathit{\Upsilon }}_{\mathrm{*}}\left(\varkappa, \mathcal{i}\right) = \mathcal{i}\varkappa, {\mathit{\Upsilon }}^{\mathrm{*}}\left(\varkappa, \mathcal{i}\right) = (2-\mathcal{i})\varkappa and {\mathcal{J}}_{\mathcal{*}}\left(\varkappa, \mathcal{i}\right) = \left(1-\mathcal{i}\right)\varkappa +2\mathcal{i} , {\mathcal{J}}^{\mathcal{*}}\left(\varkappa, \mathcal{i}\right) = \left(1-\mathcal{i}\right)\left(8-{e}^{\varkappa }\right)+2\mathcal{i} {\lambda }_{1}, {\lambda }_{2} -convex functions for each \mathcal{i}\in [0, \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }1] . Hence \widetilde {\mathit{\Upsilon }}, \widetilde {\mathcal{J}} both are up and down \lambda -convex fuzzy-number valued mappings. We now computing the following
for each \mathcal{i}\in \left[0, 1\right], that means
Hence, Theorem 7 is demonstrated.
Theorem 8. Let \widetilde {\mathit{\Upsilon }}, \widetilde {\mathcal{J}}:\left[\tau, \vartheta \right]\to {\mathbb{E}}_{C} be two up and down {\lambda }_{1} -convex and {\lambda }_{2} -convex fuzzy-number valued mappings with non-negative real-valued functions {\lambda }_{1}, {\lambda }_{2}:[0, 1]\to {\mathbb{R}}^{+} , respectively and {\lambda }_{1}\left(\frac{1}{2}\right){\lambda }_{2}\left(\frac{1}{2}\right)\ne 0, respectively, whose \mathcal{i} -levels define the family of i-v-ms {\mathit{\Upsilon }}_{\mathcal{i}}, {\mathcal{J}}_{\mathcal{i}}:\left[\tau, \vartheta \right]\subset \mathbb{R}\to {\mathcal{X}}_{I}^{+} are given, respectively, by {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[{\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right), {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right)\right] and {\mathcal{J}}_{\mathcal{i}}\left(\varkappa \right) = \left[{\mathcal{J}}_{\mathcal{*}}\left(\varkappa, \mathcal{i}\right), {\mathcal{J}}^{\mathcal{*}}\left(\varkappa, \mathcal{i}\right)\right] for all \varkappa \in \left[\tau, \vartheta \right] and for all \mathcal{i}\in \left[0, 1\right] . If \widetilde {\mathit{\Upsilon }}\otimes \widetilde {\mathcal{J}}\in {\mathcal{F}\mathcal{A}}_{\left(\left[\tau, \vartheta \right], \mathcal{i}\right)} , then
where \widetilde {\mathcal{M}}\left(\tau, \vartheta \right) = \widetilde {\mathit{\Upsilon }}\left(\tau \right)\otimes \widetilde {\mathcal{J}}\left(\tau \right) \oplus \widetilde {\mathit{\Upsilon }}\left(\vartheta \right)\otimes \widetilde {\mathcal{J}}\left(\vartheta \right), \widetilde {\mathcal{N}}\left(\tau, \vartheta \right) = \widetilde {\mathit{\Upsilon }}\left(\tau \right)\otimes \widetilde {\mathcal{J}}\left(\vartheta \right) \oplus \widetilde {\mathit{\Upsilon }}\left(\vartheta \right)\otimes \widetilde {\mathcal{J}}\left(\tau \right), and {\mathcal{M}}_{\mathcal{i}}\left(\tau, \vartheta \right) = \left[{\mathcal{M}}_{\mathcal{*}}\left(\left(\tau, \vartheta \right), \mathcal{i}\right), {\mathcal{M}}^{\mathcal{*}}\left(\left(\tau, \vartheta \right), \mathcal{i}\right)\right] and {\mathcal{N}}_{\mathcal{i}}\left(\tau, \vartheta \right) = \left[{\mathcal{N}}_{\mathcal{*}}\left(\left(\tau, \vartheta \right), \mathcal{i}\right), {\mathcal{N}}^{\mathcal{*}}\left(\left(\tau, \vartheta \right), \mathcal{i}\right)\right].
Proof. By hypothesis, for each \mathcal{i}\in \left[0, 1\right], we have
Integrating over \left[0, 1\right], we have
that is
hence, the required result.
Example 5. We consider {\lambda }_{1}\left(\varsigma \right) = \varsigma, {\lambda }_{2}\left(\varsigma \right) = \varsigma, for \varsigma \in \left[0, 1\right] , and the fuzzy-number valued mappings \widetilde {\mathit{\Upsilon }}, \widetilde {\mathcal{J}}:\left[\tau, \vartheta \right] = \left[0, 1\right]\to {\mathbb{E}}_{C}, as in Example 4. Then, for each \mathcal{i}\in \left[0, 1\right], we have {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[\mathcal{i}\varkappa, (2-\mathcal{i})\varkappa \right] and {\mathcal{J}}_{\mathcal{i}}\left(\varkappa \right) = \left[\left(1-\mathcal{i}\right)\varkappa +2\mathcal{i}, \left(1-\mathcal{i}\right)\left(8-{e}^{\varkappa }\right)+2\mathcal{i}\right] and, \widetilde {\mathit{\Upsilon }}\left(\varkappa \right), \widetilde {\mathcal{J}}\left(\varkappa \right) are up and down {\lambda }_{1} -convex and up and down {\lambda }_{2} -convex fuzzy-number valued mappings, respectively. We have {\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right) = \mathcal{i}\varkappa, {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right) = (2-\mathcal{i})\varkappa and {\mathcal{J}}_{\mathcal{*}}\left(\varkappa, \mathcal{i}\right) = \left(1-\mathcal{i}\right)\varkappa +2\mathcal{i} , {\mathcal{J}}^{\mathcal{*}}\left(\varkappa, \mathcal{i}\right) = \left(1-\mathcal{i}\right)\left(8-{e}^{\varkappa }\right)+2\mathcal{i} . We now computing the following
for each \mathcal{i}\in \left[0, 1\right], that means
hence, Theorem 8 is demonstrated.
The H-H Fejér inequalities for up and down \lambda -convex fuzzy number valued mappings are now presented. The second H-H Fejér inequality for up and down \lambda -convex fuzzy number valued mapping is firstly obtained.
Theorem 9. Let \widetilde {\mathit{\Upsilon }}:\left[\tau, \vartheta \right]\to {\mathbb{E}}_{C} be an up and down \lambda -convex fuzzy number valued mapping with \lambda :[0, 1]\to {\mathbb{R}}^{+} , whose \mathcal{i} -levels define the family of i-v-ms {\mathit{\Upsilon }}_{\mathcal{i}}:\left[\tau, \vartheta \right]\subset \mathbb{R}\to {\mathcal{X}}_{I}^{+} are given by {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[{\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right), {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right)\right] for all \varkappa \in \left[\tau, \vartheta \right] and for all \mathcal{i}\in \left[0, 1\right] . If \widetilde {\mathit{\Upsilon }}\in {\mathcal{F}\mathcal{R}}_{\left(\left[\tau, \vartheta \right], \mathcal{i}\right)} and \mathfrak{B}:\left[\tau, \vartheta \right]\to \mathbb{R}, \mathfrak{B}\left(\varkappa \right)\ge 0, symmetric with respect to \frac{\tau +\vartheta }{2}, then
Proof. Let \widetilde {\mathit{\Upsilon }} be an up and down \lambda -convex fuzzy number valued mapping. Then, for each \mathcal{i}\in \left[0, 1\right], we have
And
After adding (44) and (45), and integrating over \left[0, 1\right], we get
Since \mathfrak{B} is symmetric, then
Since
Then from (47), (46) we have
that is
hence
Now, generalizing the first H-H Fejér inequalities for classical convex functions and we build the first H-H Fejér inequality for up and down \lambda -convex fuzzy number valued mapping.
Theorem 10. Let \widetilde {\mathit{\Upsilon }}:\left[\tau, \vartheta \right]\to {\mathbb{E}}_{C} be an up and down \lambda -convex fuzzy number valued mapping with \lambda :[0, 1]\to {\mathbb{R}}^{+} , whose \mathcal{i} -levels define the family of i-v-ms {\mathit{\Upsilon }}_{\mathcal{i}}:\left[\tau, \vartheta \right]\subset \mathbb{R}\to {\mathcal{X}}_{I}^{+} are given by {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[{\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right), {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right)\right] for all \varkappa \in \left[\tau, \vartheta \right] and for all \mathcal{i}\in \left[0, 1\right] . If \widetilde {\mathit{\Upsilon }}\in {\mathcal{F}\mathcal{R}}_{\left(\left[\tau, \vartheta \right], \mathcal{i}\right)} and \mathfrak{B}:\left[\tau, \vartheta \right]\to \mathbb{R}, \mathfrak{B}\left(\varkappa \right)\ge 0, symmetric with respect to \frac{\tau +\vartheta }{2}, and {\int }_{\tau }^{\vartheta }\mathfrak{B}\left(\varkappa \right)d\varkappa > 0 , then
Proof. Since \widetilde {\mathit{\Upsilon }} is an up and down \lambda -convex, then for \mathcal{i}\in \left[0, 1\right], we have
Since \mathfrak{B}\left(\varsigma \tau +\left(1-\varsigma \right)\vartheta \right) = \mathfrak{B}\left(\left(1-\varsigma \right)\tau +\varsigma \vartheta \right) , then by multiplying (48) by \mathfrak{B}\left(\left(1-\varsigma \right)\tau +\varsigma \vartheta \right) and integrate it with respect to \varsigma over \left[0, 1\right], we obtain
Since
Then from (51), (50) we have
from which, we have
that is
This completes the proof.
Remark 6. From Theorem 9 and 10, we clearly see that:
If \mathfrak{B}\left(\varkappa \right) = 1 , then we acquire the inequality (25).
Let \mathcal{i} = 1 and \lambda \left(\varsigma \right) = \varsigma . Then from (43) and (48), we acquire the following inequality, see [1]:
If \widetilde {\mathit{\Upsilon }} is lower up and down convex fuzzy-number valued mapping on [\tau, \vartheta] and \lambda \left(\varsigma \right) = \varsigma, then we acquire the following coming inequality, see [33]:
If \widetilde {\mathit{\Upsilon }} is lower up and down convex fuzzy-number valued mapping on [\tau, \vartheta] with \mathcal{i} = 1 and \lambda \left(\varsigma \right) = \varsigma, then from (43) and (48) we acquire the following coming inequality, see [45]:
If \widetilde {\mathit{\Upsilon }} is lower up and down convex fuzzy-number valued mapping on [\tau, \vartheta] with \mathcal{i} = 1 and \lambda \left(\varsigma \right) = \varsigma , then from (43) and (48) we acquire the following coming inequality, see [45]:
Let \lambda \left(\varsigma \right) = \varsigma, and {\mathit{\Upsilon }}_{*}(\varkappa, \mathcal{i}) = {\mathit{\Upsilon }}^{*}(\varkappa, \mathcal{i}) with \mathcal{i} = 1 . Then from (43) and (48), we obtain following classical Fejér inequality.
Example 6. We consider \lambda \left(\varsigma \right) = \varsigma, for \varsigma \in \left[0, 1\right] , and the fuzzy-number valued mapping {\mathit{\Upsilon }}:\left[0, 2\right]\to {\mathbb{E}}_{C} defined by,
Then, for each \mathcal{i}\in \left[0, 1\right], we have {\mathit{\Upsilon }}_{\mathcal{i}}\left(\varkappa \right) = \left[\left(1-\mathcal{i}\right)\left(2-{\varkappa }^{\frac{1}{2}}\right)+\frac{3}{2}\mathcal{i}, \left(1-\mathcal{i}\right)\left(2+{\varkappa }^{\frac{1}{2}}\right)+\frac{3}{2}\mathcal{i}\right] . Since end point mappings {\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right), {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right) are convex mappings for each \mathcal{i}\in [0, 1] , then {\mathit{\Upsilon }}\left(\varkappa \right) is up and down convex fuzzy-number valued mapping. If
then \mathfrak{B}\left(2-\varkappa \right) = \mathfrak{B}\left(\varkappa \right)\ge 0 , for all \varkappa \in \left[0, 2\right] . Since {\mathit{\Upsilon }}_{*}\left(\varkappa, \mathcal{i}\right) = \left(1-\mathcal{i}\right)\left(2-{\varkappa }^{\frac{1}{2}}\right)+\frac{3}{2}\mathcal{i} and {\mathit{\Upsilon }}^{*}\left(\varkappa, \mathcal{i}\right) = \left(1-\mathcal{i}\right)\left(2+{\varkappa }^{\frac{1}{2}}\right)+\frac{3}{2}\mathcal{i} . Now we compute the following:
And
From (57) and (58), we have
\left[\frac{\mathcal{i}+5}{12}+\frac{1}{24}\left[3\pi \left(\mathcal{i}-1\right)-4\left(\mathcal{i}-4\right)\right], \frac{1}{12}\left[11-5\mathcal{i}\right]+\frac{1}{24}\left[-3\pi \mathcal{i}-4\mathcal{i}+3\pi +16\right]\right] {\supseteq }_{I}\left[\frac{1}{3}\left(4\left(1-\mathcal{i}\right)-\sqrt{2}\left(1-\mathcal{i}\right)+3\mathcal{i}\right), \frac{1}{3}\left(4\left(1-\mathcal{i}\right)+\sqrt{2}\left(1-\mathcal{i}\right)+3\mathcal{i}\right)\right], for all \mathcal{i}\in \left[0, 1\right].
Hence, Theorem 9 is verified.
For Theorem 10, we have
From (59) and (60), we have
Hence, Theorem 10 has been verified.
4.
Conclusions
In this work, the class of up and down \lambda -convex fuzzy-number valued mappings is introduced s an extension of classical convex functions and some new Hermite-Hadamard inequalities are established by means of fuzzy order relation on fuzzy-number space. Useful examples that verify the applicability of theory developed in this study are presented. We intend to use various types of up and down convex fuzzy-number valued mappings to construct fuzzy inequalities for fuzzy-number valued mappings. We hope that this concept will be helpful for other authors to pay their roles in different fields of sciences. Future work will explore fuzzy fractional integrals to study H-H type and weighted H-H type fuzzy inclusions for up and down convex fuzzy-number valued mappings.
Acknowledgments
The authors would like to thank the Rector, COMSATS University Islamabad, Islamabad, Pakistan, for providing excellent research and academic environments. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4330052DSR12 and also, the research was funded by the project ProCode-UCM (PID2019-108528RB-C22) from the Spanish Ministerio de Ciencia e Innovación.
Conflict of interest
The authors declare that they have no competing interests.


















 DownLoad:
DownLoad: