Analyzing Chebyshev polynomial-based geometric circulant matrices

1.   Introduction

Circulant matrices, a special subclass of Toeplitz matrices, exhibit a unique property where each row is a circular shift of the first row. Represented as $C = \mathrm{Circ}(c_0, c_1, \ldots, c_{n-1})$ or simply $C = \mathrm{Circ}(v)$, these matrices are fully determined by a single vector $v = (c_0, c_1, \ldots, c_{n-1})^T\in\mathbb{C}^n$. The matrix entries follow a simple rule:

This structured nature lends itself to efficient computation and manipulation, similar to other structured matrices. Although circulant matrices have been known for a long time, their detailed exploration began with Davis' monograph in 1979 ^[1]. For further insights into this matrix class, references such as ^[2,3] are valuable.

Circulant matrices exhibit various intriguing properties, particularly their diagonalization by the discrete fourier transform (DFT), which renders them important across a wide range of disciplines.

These matrices facilitate efficient computation and straightforward manipulation of eigenvectors and eigenvalues. Notably, their multiplication can be efficiently computed using the fast fourier transform (FFT) algorithm ^[4], which proves advantageous in convolution operations and solving linear systems of structured type ^{[5,6,7,8,9,10]}. Additionally, circulant matrices display favorable characteristics concerning their eigenvectors and eigenvalues (in ^[11] the eigenvalues of circulant approximations to Toeplitz matrices are used for computing the eigenvalues of specific Toeplitz matrices), closely tied to cyclic groups in abstract algebra ^[12], thereby establishing connections with group theory. Circulant matrices find applications in various fields such as number theory, time series analysis, signal processing, cryptography, and deep learning algorithms ^{[13,14,15,16,17]}. It is worth observing that $r$-circulant matrices and their block versions have been used in a numerical analysis framework for approximating shift-invariant (Toeplitz) operators also in the context of (fractional) differential equations and subdivision schemes, and in these fields $r$ is usually complex of modulus 1 (see ^{[6,7,8,9,10,18]} and references therein) or of very small but positive modulus when approximating triangular Toeplitz matrices using parallel algorithms (see ^[18] and references therein).

Moreover, circulant matrices have several generalizations and variations customized for specific applications, including skew circulant matrices, almost circulant matrices, random circulant matrices, block circulant matrices, and geometric circulant matrices, among others. Particularly, $r$-circulant matrices, denoted as $C_r = \mathrm{Circ}_r(c_0, c_1, \ldots, c_{n-1})$, have attracted significant interest in recent years. These matrices, whose entries are defined by:

besides the given vector, are also characterized by a fixed complex number $r$. They offer extensive research possibilities, especially regarding their norms, when the entries of the vector $v$ are some well-known integer sequences. This topic has received considerable attention, with numerous studies addressing these matrices; interested readers can refer to works such as ^{[7,8,9,18,19,20,21,22,23,24,25,26,27,28,29,30]} for further information.

In this paper, we examine geometric circulant matrices^* and explore their norm properties, with a focus on advancing current results.

^*We suggest the term "geometric $r-$circulant matrix" for a more descriptive characterization, though we will adhere to established notation.

2.   Background material

2.1.   Geometric circulant matrices

To distinguish between circulant matrices containing geometric sequences and geometric circulant matrices, let us formally define the latter ^[31]:

Definition 1. For $n\geqslant 2$, $v = (c_0, c_1, \ldots, c_{n-1})^T\in\mathbb{C}^n$, and $r\in\mathbb{C}$, a matrix $C_{r^*}\in\mathbb{M}_n(\mathbb{C})$, also denoted as $\mathrm{Circ}_{r^*}(c_0, c_1, \ldots, c_{n-1})$, is called a geometric circulant matrix if it has the following form:

Additionally, in ^[31], the authors determined the bounds for the spectral norms in cases where the geometric circulant matrix contains generalized Fibonacci numbers and hyper-harmonic Fibonacci numbers. In the paper ^[32], the authors defined the hyper-Horadam sequence and obtained upper and lower bounds for the spectral norm of geometric circulant matrices involving these numbers. Spectral norms of geometric circulant matrices with generalized $k-$Horadam numbers and with trigonometric functions were studied by Shi ^[26,27].

To avoid trivial cases, we always assume $r\neq 0$ in (2.1), as $r = 0$ would yield a Toeplitz upper triangular matrix. Note that the results presented herein are also applicable to ordinary circulant matrices (i.e., when $r = 1$).

The square of the Frobenius norm of the matrix $C_{r^*}$ can be expressed as:

We aim to simplify this formula, particularly when the matrix $C_{r^*}$ incorporates various integer sequences, by employing the Chebyshev polynomials of the first and second kind. Before this, let us point out the well-established inequality (as observed in ^[33]) regarding norms:

where $\|C_{r^*}\|_2$ denotes the spectral norm, i.e., $\|C_{r^*}\|_2\, = \, \max_{1\leqslant k\leqslant n}\sigma_k(C_{r^*})$, with $\sigma_k$ being the $k-$th singular value of $C_{r^*}$. Here, $\|C_{r^\ast}\|_F = \sqrt{\sum_{k = 1}^n\sigma_k^2(C_{r^\ast})}$.

2.2.   Chebyshev polynomials, $r$-circulant matrices, and their applications

In the paper ^[20], the authors established a significant connection between two important areas of applied mathematics: Chebyshev polynomials and $r$-circulant matrices, yielding compelling results. They demonstrated how utilizing Chebyshev polynomials of the first and second kind can improve existing results in the study of these matrices.

Chebyshev polynomials are fundamental across various fields due to their orthogonality and unique ability to minimize maximum approximation errors. They play a crucial role in numerical analysis, signal processing, and computational mathematics where their precision in mathematical modeling and analysis is highly effective. Comprehensive overviews of this topic can be found in books such as ^[34,35]. Their applications extend into image processing, facilitating efficient shape and texture recognition as well as image compression algorithms, thereby supporting advancements in AI systems ^[36,37]. Moreover, recent research highlights their relevance in geometric deep learning ^[38,39,40], underscoring their versatility in modern mathematical and computational contexts.

Now, let us briefly introduce the definitions that will be used. Among several equivalent definitions of these polynomials, we adopt a recursive definition. Since this paper deals with complex polynomials, we will give a brief explanation of the definition of the Chebyshev polynomials for a complex variable.

As is well-known, the mapping $\omega\mapsto\frac{1}{2}(\omega+\omega^{-1})$ is a conformal mapping from the punctured open unit disk $\{\omega\in\mathbb{C}\mid 0 < |\omega| < 1\}$ onto $\mathbb{C}\setminus[-1, 1]$. Note that $0 < |\omega| < 1$ if and only if $|\omega^{-1}| > 1$. Hence, for every $z\in\mathbb{C}\setminus[-1, 1]$, we can associate a complex number $\omega$ such that:

If $|\omega| = 1$, then $\mathrm{Im}(z) = 0$, i.e., $z = x\in[-1, 1]$ is real, and this case will be considered separately.

Definition 2. For a non-negative integer $n$ and a complex variable $z$, the Chebyshev polynomials of the first and second kind are defined as follows:

If $z\in(-\infty, -1)\cup(1, +\infty)$, then both $\omega$ and $\omega^{-1}$ are real numbers, which implies that ${\mathsf{T}}_n(z)$ and ${\mathsf{U}}_n(z)$ are also real. When $z\in[-1, 1]$, the expressions become ${\mathsf{T}}_n(z) = \cos n\theta$ and ${\mathsf{U}}_n(z) = \sin(n+1)\theta/\sin\theta$, where $\theta$ is such that $z = \cos\theta$ (see ^[34] for details). In this case, ${\mathsf{T}}_n(z)$ and ${\mathsf{U}}_n(z)$ are also real numbers. Let us first recall a result from ^[20] that will be used further.

Proposition 1. [20,Proposition 3.4.] For any $z\in\mathbb{C}\setminus[-1, 1]$, there exist real numbers $k_{\mathsf{T}}, k_{\mathsf{U}}\geqslant 1$ such that $|{\mathsf{T}}_n(z)|\geqslant k_{\mathsf{T}}^{-1}$ and $|{\mathsf{U}}_n (z)|\geqslant k_{\mathsf{U}}^{-1}$ for every non-negative integer $n$. More precisely,

$1)$ If $|z|\geqslant 1$, then $k_{\mathsf{T}} = k_{\mathsf{U}} = 1$.

$2)$ If $0 < |z| < 1$, $z = (\omega+\omega^{-1})/2$, and $|\omega| > 1$, then:

$2.1)$ $k_{\mathsf{T}} = \dfrac{2|\omega|}{|\omega|^2-1}$ for the Chebyshev polynomials of the first kind.

$2.2)$ $k_{\mathsf{U}} = \dfrac{|\omega|}{|\omega|^2-1}$ for the Chebyshev polynomials of the second kind.

For the purposes of further exposition, let $z = \frac{1}{2}(\omega+\omega^{-1})$, where $z$ is a non-zero complex number. Define two sets, $Q_1$ and $Q_2$, and two associated real numbers, $x_1$ and $x_2$:

3.   Preliminaries

For every $z\in\mathbb{C}$ and every $n\geqslant 1$, let us denote by $H_n$ and $G_n$ the following polynomials:

The following are some detailed calculations required to prove the main results. Due to their volume but straightforward nature, we will introduce appropriate notations to abbreviate them where possible.

Let $z = \frac{1}{2}(\omega+\omega^{-1})\in \mathbb{C} \setminus [-1, 1]$, where $|\omega| > 1$, and $q \in \mathbb{R}^+$. Introduce the notation:

where $P_n$ denotes either $H_n$ or $G_n$. If $x\in[-1, 1]$, then $x = \frac{1}{2}(\omega+\omega^{-1})\in[-1, 1]$ for some $\omega = e^{i\varphi},$ $\varphi\in[0, 2\pi).$ Then $|\omega| = |\omega|^{-1} = 1$, and for $q \in \mathbb{R}^+$ we denote:

Lemma 1. For $z = \frac{1}{2}(\omega + \omega^{-1}) \in \mathbb{C} \setminus [-1, 1]$, where $|\omega| > 1$ and $q \in \mathbb{R}^+$, the following holds for $i = 1, 2$:

Proof. For $i = 1$ and $q^2\notin\left\{|\omega|^2, |\omega|^{-2}\right\}$:

For $i = 1$ and $q^2 = |\omega|^2$:

Similarly, the formula applies when $i = 1$ and $q^2 = |\omega|^{-2}$. The case for $i = 2$ follows in the same manner. □

Remark 1. Note that in the second case, $q^2\in Q_2$ implies that $\omega^2|\omega|^{-2}$ and $\omega^{-2}|\omega|^2$ are real numbers. Actually, we have $\omega^2|\omega|^{-2} = \omega^{-2}|\omega|^2 = 1$, which means $Q_2 = \{1\}$ and hence $q^2 = 1$.

Lemma 2. For $x = \frac{1}{2}(\omega + \omega^{-1}) \in [-1, 1]$ and $q \in \mathbb{R}^+$, the following holds:

Proof. If $q^2\notin\{\omega^2, \, \omega^{-2}\}$, then $\omega^2 q^2 \neq 1$ and $\omega^{-2} q^2 \neq 1$. Therefore,

When $q^2\in\{\omega^2, \, \omega^{-2}\}$ and $q\neq1$, for the polynomial $H_{n, 3}$, we have $H_{n, 3}(x, q) = n+(q^{4n}-1)(q^4-1)^{-1}$. If $q^2\in\{\omega^2, \, \omega^{-2}\}$, and $q = 1$, i.e., $x\in\{-1, 1\}$, then $H_{n, 3}(x, q) = 2n$. □

Proposition 2. Suppose $z = \frac{1}{2}(\omega+\omega^{-1})$, $n\geqslant 2$, $|\omega| > 1$ (i.e., $z\in\mathbb{C}\setminus[-1, 1]$), and $q\in\mathbb{R}^+$. Then we have:

If $z = x\in[-1, 1]$ and $q\in\mathbb{R}^+$, the expressions simplify as follows:

Proof. The required results can be obtained through direct calculation. For the first sum $s_n^{\mathsf{T}}(z, q^2)$, we have:

For the second sum $s_n^{\mathsf{U}}(z, q)$, note that $(\omega-\omega^{-1})(\overline{\omega}-\overline{\omega}^{-1}) = |\omega-\omega^{-1}|^2 = 4|z^2-1|$. Therefore,

The summation formula now follows according to the introduced notations.

Consider the case when $|\omega| = 1$, i.e., when $z = x\in[-1, 1]$. For the Chebyshev polynomials of the first kind, we have:

Further calculation of the required sums involving the Chebyshev polynomials of the second kind follows a similar methodology as for the Chebyshev polynomials of the first kind, but will not be detailed here. □

Define

for $i = 1, 2$. For $z = \frac{1}{2}(\omega+\omega^{-1})\in\mathbb{C}\setminus[-1, 1]$, where $|\omega| > 1$ and $q\in\mathbb{R}^+$, we have:

The proof of (3.11) involves straightforward calculations, similar to those in Eq (3.5). Similarly, akin to those in Eq (3.6), we obtain:

Proposition 3. Suppose $z = \frac{1}{2}(\omega+\omega^{-1})$, $n\geqslant 2$, $|\omega| > 1$ (i.e., $z\in\mathbb{C}\setminus[-1, 1]$), and $q\in\mathbb{R}^+$. Then we have:

If $x\in[-1, 1]$ and $q\in\mathbb{R}^+$ the summation formulas simplify to:

The proof of the previous proposition involves straightforward computations according to the introduced notation and will be omitted. Instead, in Section 5, we illustrate how these results can be applied through examples involving some important integer sequences: Fibonacci numbers $\{{\mathsf{F}}_n\}$, Lucas numbers $\{{\mathsf{L}}_n\}$, and Pell numbers $\{{\mathsf{P}}_n\}$, which are connected to the Chebyshev polynomials as follows (see, e.g., ^{[41,42,43,44]}):

for $n\in\{0, 1, 2, \ldots\}$.

4.   Estimating spectral norms of geometric circulant matrices

In this section, we present our main results regarding the lower and upper bounds of the spectral norms of geometric circulant matrices based on previous calculations. Specifically, we investigate the norms of the matrices: $C_{\mathsf{T}} = \mathrm{Circ}_{r^{\ast}}\left({\mathsf{T}}_0(z), {\mathsf{T}}_1(z), \ldots, {\mathsf{T}}_{n-1}(z)\right)$, $C_{\mathsf{U}} = \mathrm{Circ}_{r^{\ast}}\left({\mathsf{U}}_0(z), {\mathsf{U}}_1(z), \ldots, {\mathsf{U}}_{n-1}(z)\right)$, where $n\geqslant 2$ is a positive integer and $z$ is an arbitrary non-zero complex number.

Due to the distinctive properties of the real Chebyshev polynomials compared to complex ones, we will present our main results in separate theorems.

4.1.   Frobenius norm

The Frobenius norm of these matrices can be explicitly calculated. The following theorem applies.

Theorem 1. Let $n\geqslant 2$ be an integer, $z\in\mathbb{C}\setminus[-1, 1]$ such that $z = \frac{1}{2}(\omega+\omega^{-1})$ and $|\omega| > 1$. Let $\{P_n(z)\}_{n\geqslant 0}$ and $\{Q_n(z)\}_{n\geqslant 0}$ be sequences of complex numbers such that $\left|P_k(z)\right| = \left|{\mathsf{T}}_k(z)\right|$ and $\left|Q_k(z)\right| = \left|{\mathsf{U}}_k(z)\right|$, for $k = 0, 1, \ldots, n-1$. If $C_1 = \mathrm{Circ}_{r^{\ast}}\left(P_{0}(z), P_{1}(z), \ldots, P_{n-1}(z)\right)$ and $C_2 = \mathrm{Circ}_{r^{\ast}}\left(Q_{0}(z), Q_{1}(z), \ldots, Q_{n-1}(z)\right)$, then we have:

Proof. The proof follows immediately by applying Propositions 2 and 3 to equality (2.2). □

An analogous theorem on the Frobenius norm holds for real numbers in the interval $[-1, 1]$ under slightly milder conditions. We will state this theorem for later applications in the paper.

Theorem 2. For matrices $C_3 = \mathrm{Circ}_{r^{\ast}}\left(P_{0}(x), \ldots, P_{n-1}(x)\right)$ and $C_4 = \mathrm{Circ}_{r^{\ast}}\left(Q_{0}(x), \ldots, Q_{n-1}(x)\right)$, where $n\geqslant 2$ is an integer, $x\in[-1, 1]$ is a real number, and for every $k = 0, 1, \ldots, n-1$ such that $|P_k(x)| = |{\mathsf{T}}_k(x)|$ and $|Q_k(x)| = |{\mathsf{U}}_k(x)|$, we have:

4.2.   Spectral norm estimation

When estimating the spectral norm of a matrix, an essential tool is the inequality

where $r_1(A)$ denotes the maximum row Euclidean norm of matrix $A$, and $c_1(B)$ denotes the maximum column Euclidean norm of matrix $B$. Here, $A\circ B$ denotes the Hadamard (element-wise) product of matrices $A$ and $B$. This inequality was established by Horn and Mathias ([46,Theorem 1.2.]), and we will refer to it several times.

Theorem 3. Let $x\in[-1, 1]$ be a real number, $r\ne 0$ be a complex number, $n\geqslant 2$ be an integer, and $\{P_n(x)\}_{n\geqslant 0}$ and $\{Q_n(x)\}_{n\geqslant 0}$ be sequences of real numbers such that $\left|P_k(x)\right| = \left|{\mathsf{T}}_k(x)\right|$ and $\left|Q_k(x)\right| = \left|{\mathsf{U}}_k(x)\right|$ for every $k = 0, 1, \ldots, n-1$. Define matrices $C_1 = \mathrm{Circ}_{r^{\ast}}\left(P_{0}(x), P_{1}(x), \ldots, P_{n-1}(x)\right)$ and $C_2 = \mathrm{Circ}_{r^{\ast}}\left(Q_{0}(x), Q_{1}(x), \ldots, Q_{n-1}(x)\right)$.

If $|r| > 1$, then the following inequalities hold:

If $|r| \leqslant 1$, the inequality $\textrm{(2.3)}$ is applicable.

The same estimates apply when the matrix $C_1$ is replaced by the matrix $C_2$ and when the sum $s^{\mathsf{T}}_{n}$ is replaced by $s^{\mathsf{U}}_{n}$.

Proof. To prove the inequality for the spectral norm of the matrix $C_1$ involving polynomials $P_i(x)$ related to the Chebyshev polynomials of the first kind, we will consider only the case when $|r| > 1$. Starting with the inequality derived from (2.3) and Theorem 4.2:

For the upper bound, consider the Hadamar product $C_1 = A\circ B$, where $A = \mathrm{Circ}_{r^{\ast}}\left(1, 1, \ldots, 1\right)$ and $B = \mathrm{Circ}\left(P_{0}(x), P_{1}(x), \ldots, P_{n-1}(x)\right)$:

According to (4.1), we have $\|C_1\|_2\leq\sqrt{H_n(|r|)s_{n}^{\mathsf{T}}(x, 1)}$. Combining this with the upper bound in (2.3), we obtain:

The estimation of the bounds of the norms of the matrix $C_2$, containing the Chebyshev polynomials of the second kind, follows a similar approach to the matrix $C_1$, with adjustments to the polynomials and sums used. □

Remark 2. The upper bound of the spectral norm in the previous theorem requires additional explanation. In many studies determining the upper bound of the spectral norm when $|r|\leqslant 1$, the Hadamard product of matrices $A$ and $B$, as described in the proof of Theorem 4.3, is typically considered. For these matrices, $r_1(A) = \sqrt{n}$ and $c_1(B) = \sqrt{s_{n}^{\mathsf{T}}(x, 1)}$, leading to $\|C_1\|_2\leq\sqrt{ns_{n}^{\mathsf{T}}(x, 1)}$, which holds true. However, (2.3) provides a more refined estimate due to:

since $|r|^{2n-2k}-1\leqslant 0$ for $|r|\leqslant 1$, $k\in\{0, 1, \ldots, n-1\}$, and $n\geqslant 2$.

Example 1. Consider the following geometric circulant matrices:

$A = \mathrm{Circ}_{r^\ast}({\mathsf{T}}_0(-1/3), {\mathsf{T}}_1(-1/3), {\mathsf{T}}_2(-1/3), {\mathsf{T}}_3(-1/3))$ and $B = \mathrm{Circ}_{r^\ast}({\mathsf{U}}_0(-1/3), {\mathsf{U}}_1(-1/3), {\mathsf{U}}_2(-1/3), {\mathsf{U}}_3(-1/3))$. The following table shows the lower bounds (LB), upper bounds (UB), and exact spectral norms for matrices $A$ and $B$ for different values of the complex number $r$. The lower and upper bounds (LB and UB) are obtained using Theorem 3.

Example 2. Let $C = \mathrm{Circ}_{r^\ast}({\mathsf{T}}_0(1/2), {\mathsf{T}}_1(1/2), {\mathsf{T}}_2(1/2), {\mathsf{T}}_3(1/2), {\mathsf{T}}_4(1/2))$ be a geometric circulant matrix, and let $D = \mathrm{Circ}_{r^\ast}({\mathsf{U}}_0(1/2), {\mathsf{U}}_1(1/2), {\mathsf{U}}_2(1/2), {\mathsf{U}}_3(1/2), {\mathsf{U}}_4(1/2))$, i.e.,

The obtained results are presented in the following table:

where the lower and upper bounds (LB and UB) are obtained using Theorem 3.

Theorem 4. Let $n \geqslant 2$ be an integer, and let $z \in \mathbb{C} \setminus [-1, 1]$ be such that $z = \frac{1}{2}(\omega + \omega^{-1})$ with $|\omega| > 1$. Consider sequences $\{P_n(z)\}_{n \geqslant 0}$ and $\{Q_n(z)\}_{n \geqslant 0}$ of complex numbers such that $\left|P_k(z)\right| = \left|{\mathsf{T}}_k(z)\right|$ and $\left|Q_k(z)\right| = \left|{\mathsf{U}}_k(z)\right|$ for every $k = 0, 1, \ldots, n-1$. Let $k_{\mathsf{T}} \geqslant 1$ as described in Proposition 1, and define matrices $C_3 = \mathrm{Circ}_{r^{\ast}}\left(P_{0}(z), P_{1}(z), \ldots, P_{n-1}(z)\right)$ and $C_4 = \mathrm{Circ}_{r^{\ast}}\left(Q_{0}(z), Q_{1}(z), \ldots, Q_{n-1}(z)\right)$.

If $|r| > 1$, then:

If $|r| \leqslant 1$, then the approximation $\text{(2.3)}$ is used.

These estimates also apply if $C_3$ is replaced by $C_4$, and $s^{\mathsf{T}}_n$, $\overline{s}^{\mathsf{T}}_n$, $k_{\mathsf{T}}$ are replaced by $s^{\mathsf{U}}_n$, $\overline{s}^{\mathsf{U}}_n$, $k_{\mathsf{U}}$ respectively.

Proof. The proof follows a similar structure to previous proofs, relying on Proposition 1. We will demonstrate the theorem for the matrix $C_3$ in the case when $|r| > 1$. Starting from inequality (2.3) and applying Theorem 4.1, we have:

Consider the Hadamard product $C_3 = A_1\circ B_1$, where matrices $A_1$ and $B_1$ are defined as:

According to Proposition 1, $|{\mathsf{P}}_i(z)| = |{\mathsf{T}}_i(z)| \geqslant 1/k$. Therefore,

Applying inequality (4.1), we obtain:

For the specific choice $A_2 = \mathrm{Circ}_{r^{\ast}}\left(1, 1, \ldots, 1\right)$ and $B_2 = \mathrm{Circ}\left(P_{0}(z), P_{1}(z), \ldots, P_{n-1}(z)\right)$, such that $C_3 = A_2\circ B_2$, we have:

With (2.3), this proves inequality (4.3) and concludes the proof for $C_3$. Similar arguments apply to $C_4$ by replacing $s^{\mathsf{T}}_n$, $\overline{s}^{\mathsf{T}}_n$, and $k_{\mathsf{T}}$ with $s^{\mathsf{U}}_n$, $\overline{s}^{\mathsf{U}}_n$, and $k_{\mathsf{U}}$ respectively. □

Remark 3. The same reasoning as in Remark 2 elucidates why the approximation (2.3) is applied when $|r| < 1$. Specifically, for $C_3 = A_2\circ B_2$, we find:

thus (2.3) provides a more refined estimate.

5.   Applications

The generalized $k$-Horadam sequence $\{{\mathsf{H}}_{k, n}\}_{n\in\mathbb{N}}$ is defined (see ^[45]) as follows:

where $n \geqslant 0$, $a, b\in\mathbb{R}$, and $f, g:\mathbb{R^+}\to\mathbb{R}$ are functions such that $f^2(k) + 4g(k) > 0$. For our purposes, one can take $f$ and $g$ to be integer-valued functions, and $a$ and $b$ to be non-negative integers. By varying the initial conditions, various integer sequences can be obtained, including the Fibonacci, Lucas, and Pell sequences as specific examples.

The paper ^[26] provides bounds for the spectral norms of geometric circulant matrices involving the generalized $k$-Horadam numbers. The main results are summarized in the following theorem, adapted with notation consistent with previous discussions;

Theorem 5.1. (^[26], Theorem 1) Let ${\mathsf{H}}_{r^*} = \mathrm{Circ}_{r^*}({\mathsf{H}}_{k, 0}, {\mathsf{H}}_{k, 1}, \ldots, {\mathsf{H}}_{k, n-1})$ be a geometric circulant matrix with entries given by the generalized $k$-Horadam numbers.

$1)$ If $|r| > 1$, then $\sqrt{\sum_{i = 0}^{n-1}{\mathsf{H}}_{k, i}^2}\leqslant\|{\mathsf{H}}_{r^*}\|_2\leqslant \sqrt{\frac{1-|r|^{2n}}{1-|r|^2}\sum_{i = 0}^{n-1}{\mathsf{H}}_{k, i}^2}.$

$2)$ If $|r|\leqslant1$, then $\sqrt{|r|^{2n}\sum_{i = 0}^{n-1}|r|^{-2i}{\mathsf{H}}^2_{k, i}}\leqslant\|{\mathsf{H}}_{r^*}\|_2\leqslant \sqrt{n\sum_{i = 0}^{n-1}{\mathsf{H}}_{k, i}^2}.$

The following examples provide improved estimates for the spectral norms of geometric circulant matrices with specific generalized $k$-Horadam numbers, compared to those in ^[26]. These examples refine the bounds by considering the specific structure of geometric circulant matrices involving the Chebyshev polynomials, offering more precise upper and lower bounds depending on the magnitude of $|r|$.

Example 3. [Fibonacci numbers] Let $\{{\mathsf{F}}_n\}$ denote the Fibonacci sequence, defined by

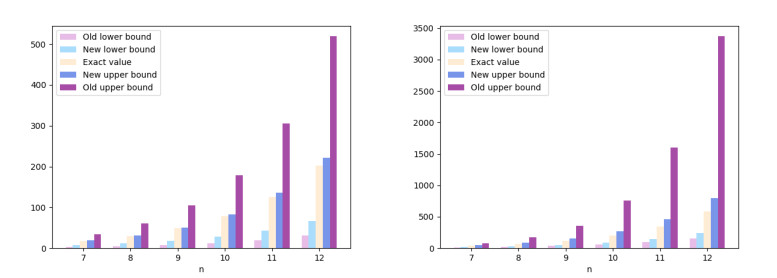
Given $z = i/2$, where $i$ is the imaginary unit, we have $\omega = \frac{1+\sqrt{5}}{2}i$, $|\omega| = \frac{1+\sqrt{5}}{2}$, $\omega|\omega|^{-1} = i$, $x_1 = \frac{\sqrt{5}}{2}$, and $x_2 = 0$. Let $C_{\mathsf{F}} = \mathrm{Circ}_{r^\ast}({\mathsf{F}}_1, {\mathsf{F}}_2, \ldots, {\mathsf{F}}_{11})$. Using the summation formula $(3.8)$ and the identity relating the Fibonacci numbers to the Chebyshev polynomials of the second kind $(3.13)$, we obtain the following results for bounds and exact values for the spectral norm of $C_{\mathsf{F}}$. The new lower bounds (LB) and new upper bounds (UB) are obtained using Theorem 4, while the old lower bounds LB and old upper bounds UB are obtained by Theorem 5.

The obtained results and improvements are illustrated in Figure 1.

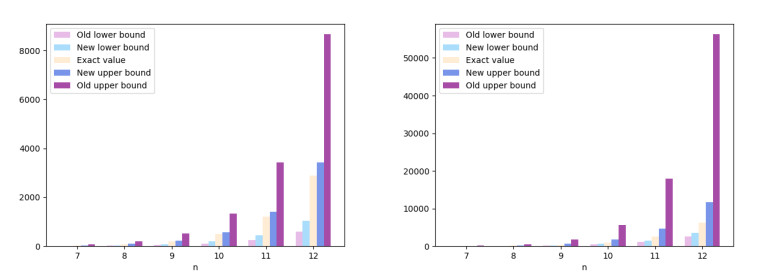
Example 4. [Lucas Numbers] Let $\{{\mathsf{L}}_n\}$ denote the Lucas sequence, defined by

As ${\mathsf{L}}_n = (2/i^n){\mathsf{T}}_n(i/2)$, similar to the previous example, with the exception of using the summation formula $(3.7)$ instead of $(3.8)$, we obtain the following bounds for the matrix $C_{\mathsf{L}} = \mathrm{Circ}_{r^\ast}({\mathsf{L}}_0, {\mathsf{L}}_1, \ldots, {\mathsf{L}}_{10})$. The same explanation for the obtained bounds applies as it did in the previous example.

The results are illustrated in Figure 2.

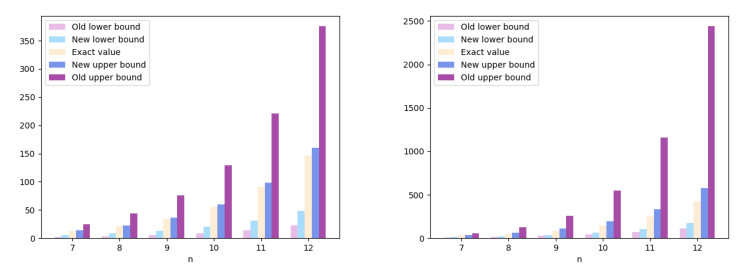
Example 5. [Pell Numbers] Let $\{{\mathsf{P}}_n\}$ denote the Pell sequence, defined by

Given $z = -i$, where $i$ is the imaginary unit, we have $\omega = 1+\sqrt{2}i$, $|\omega| = 1+\sqrt{2}$, $\omega|\omega|^{-1} = i$, $x_1 = 2\sqrt{2}$ and $x_2 = 0$. Using the summation formula $(3.8)$ and the identity $(3.13)$, for the matrix $C_{\mathsf{P}} = \mathrm{Circ}_{r^\ast}({\mathsf{P}}_0, {\mathsf{P}}_1, \ldots, {\mathsf{P}}_{10}),$ we obtain the results given in Table 5, which we illustrate with Figure 3. New lower and upper bounds (LB and UB) are derived from Theorem 4, whereas the old bounds are established through Theorem 5.

6.   Discussion

The results obtained reveal that the upper bound closely approximates the true norm value, particularly noticeable when $|r|$ is large. However, there remains potential for further enhancement of the lower bound, particularly in cases where $|r| < 1$.

7.   Conclusions

The exploration of geometric circulant matrices involving Chebyshev polynomials of the first and second kind has provided significant insights and advantages:

1) Unified Results Across Sequences. Using the properties of the Chebyshev polynomials, we have unified results across several important integer sequences, including Fibonacci, Lucas, and Pell numbers. This systematic approach provides a framework for comprehensive analysis and comparison of these sequences through their corresponding geometric circulant matrices.

2) Improved Bounds on Spectral Norms. Our method has proven effective in establishing tighter lower and upper bounds on the spectral norms of these matrices compared to previous estimates. This improvement enhances our understanding of the matrix norms involved and their implications across various applications.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We express our gratitude to the anonymous referees for their careful reading of our manuscript and their valuable suggestions, which significantly improved this paper.

Conflict of interest

All authors declare no conflicts of interest in this paper.