Estimations and optimal censoring schemes for the unified progressive hybrid gamma-mixed Rayleigh distribution

1.   Introduction

Effective control of liquid levels in storage systems is essential across various industrial processes, including chemical manufacturing, water treatment, and food processing. This task becomes particularly challenging when dealing with interacting and non-interacting tank configurations due to inherent nonlinear dynamics and complex coupling effects ^[1,2]. Maintaining precise control over fluid levels is crucial for operational safety, process efficiency, and cost reduction, necessitating advanced control strategies to manage these challenges effectively ^[3,4].

Traditional control methodologies, particularly proportional-integral (PI) and proportional-integral-derivative (PID) controllers, are widely used because of their straightforward implementation and generally adequate performance in many scenarios ^[3]. However, these controllers often fall short when addressing the nonlinear behavior and dynamic interactions characteristic of complex tank systems, leading to suboptimal performance under varying operational conditions ^[5]. To overcome these limitations, more sophisticated control techniques have been developed, including linear quadratic regulators (LQR), sliding mode control (SMC), and Wiener model-based controllers ^[6,7,8].

LQR offers optimal control by minimizing a quadratic cost function, making it suitable for systems where performance criteria can be explicitly defined in terms of state and control variables ^[9]. SMC provides robustness against parameter variations and external disturbances by driving the system states toward a predefined sliding surface ^[10]. Meanwhile, Wiener models leverage the advantages of linear control methods while approximating nonlinear dynamics, thereby providing a balance between simplicity and efficacy in handling system nonlinearities ^[11,12].

Despite the individual merits of these advanced control techniques, a comprehensive comparison of their performance in both interacting and non-interacting tank systems remains limited. Each method has its strengths and potential trade-offs depending on system characteristics and control objectives ^[13]. For instance, while PI controllers are easy to tune and implement, they may not effectively manage significant nonlinearities or dynamic coupling. LQR offers a systematic approach to optimal control but can be computationally intensive and sensitive to model accuracy. Although SMC's robustness to disturbances is advantageous, it might induce chattering in practical applications ^[14].

The aim of this paper is to evaluate each of the control algorithms for both NIS and IS. The efficacy of each control algorithm will be evaluated based on a set of performance metrics, including overshoot percentage (OS), settling time (ST), and steady-state error (SE) ^[15,16]. Through detailed modeling, controller design, and simulation, this study evaluates each controller's effectiveness under various operational conditions, including transient responses and perturbations ^[2,17].

By offering an analysis of these control strategies across different system configurations, the study provides valuable insights into their theoretical and practical implications. The findings will guide the selection of appropriate control methods based on system dynamics and desired performance outcomes, contributing to enhanced reliability and efficiency in industrial fluid storage systems ^[18,19].

The following is a description of the organization of the article. Sections 2 and 3 present an overview of the processes under study and present the dynamic models of them. Subsequently, section 4 presents a stability analysis. In sections 5 and 6, the control systems associated with the processes are designed, and the resulting simulation results are presented. In conclusion, Section 7 presents the findings of this research project.

2.   Process description

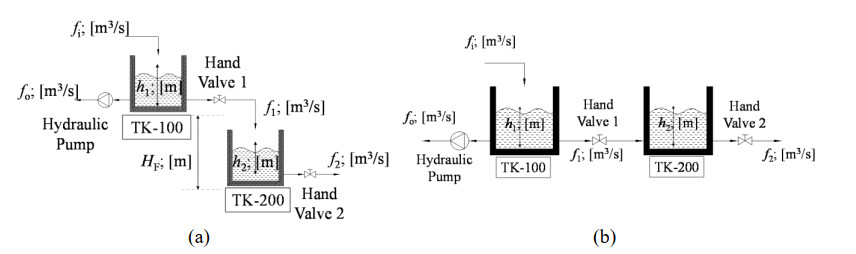
The studied process models a clean water supply plant consisting of two interconnected tanks, TK-100, and TK-200, which are configured in two distinct setups: a non-interacting system (NIS) and an interacting system (IS). The NIS configuration (see Figure 1a) arranges TK-100 and TK-200 in a cascade fashion, where each tank operates independently without influencing the other's dynamics. In contrast, the IS configuration (see Figure 1b) connects the tanks in series, allowing a dynamic interaction between them. TK-100 functions as a water accumulator, while TK-200 acts as an inertial tank, serving to mitigate fluid turbulence from TK-100 and maintain the overall system capacity ^[17].

2.1.   Tank configurations and operational dynamics

TK-100 is equipped with a loading inlet pipe and two discharge outlet pipes. The water is supplied to TK-100 via the inlet pipe at a volumetric flow rate denoted by f_i(t). This tank discharges water through two outlet pipes at flow rates f_o(t) and f₁(t), which are controlled by a hydraulic pump and hand valve (HV) 1, respectively. The hydraulic pump dynamically adjusts f_o(t) for precise flow control, whereas f₁(t) remains at a constant setting determined by HV 1.

TK-200 comprises an inlet pipe with a flow rate f₁(t) and an outlet pipe with a flow rate f₂(t), where f₂(t) is modulated by HV 2. It is crucial to note that the inlet flow rate f₁(t) of TK-200 directly corresponds to the outlet flow rate of TK-100, establishing a direct dependency between the tanks.

This dependency is a defining feature of the IS configuration, where both tanks are designed to operate at the same fluid level, facilitating a seamless interaction between them.

In the NIS configuration, TK-100 and TK-200 are separated by a fixed height H_f, ensuring that the tanks operate independently. This height differential prevents fluid from flowing from TK-200 back into TK-100, effectively decoupling their dynamic behavior.

2.2.   Process assumptions

The operation of the process is governed by the following assumptions:

• Atmospheric conditions: The entire system is assumed to be operating under standard atmospheric pressure conditions, which eliminates the need for additional pressure regulation mechanisms within the system.

• Constant temperature: The process assumes a stable ambient temperature, implying that temperature fluctuations do not affect the fluid dynamics or control parameters.

• Fixed HV openings: The openings of HV 1 and 2 are assumed to remain constant throughout the operation. This fixed setting ensures that the outlet flow rates f₁(t) and f₂(t) are only subject to changes due to the dynamics of the hydraulic pump or external disturbances.

• No backflow: There is a strict assumption of no backflow from TK-200 to TK-100, ensuring unidirectional flow through the system. This assumption simplifies the control dynamics, as it eliminates the need to account for reverse flow scenarios, particularly in the NIS configuration.

2.3.   System dynamics and control considerations

The system dynamics of both configurations are characterized by nonlinear interactions, which present unique challenges in maintaining stable fluid levels and flow rates. In the NIS setup, each tank must be independently controlled, as the absence of interaction requires precise management of individual tank dynamics to achieve the desired performance outcomes. Conversely, in the IS setup, the interaction between TK-100 and TK-200 necessitates a coordinated control strategy that accounts for the cascading effects of disturbances and the resultant impact on system stability.

TK-100's role as an accumulator introduces an inertial component to the system, where sudden changes in f_i(t) can lead to transient fluctuations that propagate through the system. This effect is especially pronounced in the IS configuration, where the interconnectedness of the tanks amplifies the influence of perturbations.

TK-200 serves as a stabilizing component, its inertial properties mitigating the turbulence introduced by TK-100. This characteristic is essential for maintaining a consistent fluid level across the system, particularly in the IS configuration, where the interdependent behavior of the tanks requires a balanced approach to control.

The study emphasizes the critical importance of selecting appropriate control methodologies to address the inherent challenges posed by these configurations. Advanced control strategies, such as PID controllers, LQR, and SMC, are evaluated for their effectiveness in managing these complex dynamics. These controllers must be adept at compensating for the nonlinearities and interaction effects characteristic of the IS setup while ensuring stable operation in the NIS configuration.

3.   Dynamic modeling of the process

The dynamic modeling of the water supply process involves establishing a mathematical representation of the system, which includes both tanks TK-100 and TK-200. The modeling is performed by applying mass conservation principles, resulting in mass balance equations for both the NIS and the IS configurations. These configurations depict how the tanks influence each other's fluid dynamics, and the equations governing these systems are derived as follows ^[17]:

3.1.   System dynamics and control considerations

For TK-100 in both configurations, the mass balance equation is expressed as:

For TK-200, the mass balance equation is represented by:

Here, ATK-100 and ATK-200 represent the cross-sectional areas of TK-100 and TK-200, respectively, measured in m². The variables f_i(t), f₁(t), and f₂(t) denote the volumetric flow rates entering and leaving the tanks, while h₁(t) and h₂(t) represent the fluid heights in TK-100 and TK-200 at time t.

3.2.   Flow rate equations for valves

According to Figure 1 and ^[17], the flow rates f₁(t) and f₂(t), which are regulated by valves, are defined for the NIS and IS configurations as follows:

For NIS:

For IS:

Here, C'_v1 and C'_v2 are the valve coefficients that account for fluid flow dynamics through the valves and are calculated as follows: C'_vx = C_vx⋅(ρ⋅g/G_f)^1/2, for x ∈ {1, 2}. In addition, C_vx is the valve discharge coefficient; ρ is the fluid density in kg/m³; g is the gravitational acceleration in m/s², and G_f is the specific gravity of the fluid.

3.3.   Nonlinear dynamic models

By substituting (3) and (4) into (1) and (2), the nonlinear dynamic models for both NIS and IS configurations are derived as follows:

For NIS:

For IS:

3.4.   Steady-state operating conditions

The steady-state operating conditions for the NIS and IS configurations can be determined by setting the derivatives in (5) and (6) to zero, resulting in the following equations:

For NIS:

For IS

where H₁^ss and H₂^ss are the steady-state fluid heights in TK-100 and TK-200, respectively. Also, F_i^ss and F_o^ss are the steady-state flow rates into and out of the system.

3.5.   Linearization of the dynamic models

To facilitate linear analysis, a Taylor series expansion is applied to linearize the nonlinear dynamic models from (6) and (7). The linearized state-space representation is given by:

Here, u(t) = [${\widehat{f}}_{\mathrm{i}}\left(t\right)$, ${\widehat{f}}_{\mathrm{o}}\left(t\right)$]^T and x(t) = [${\widehat{h}}_{1}\left(t\right)$, ${\widehat{h}}_{2}\left(t\right)$]^T are the input vector, representing deviation variables in the input flow rates, and the state vector, representing deviation variables in the fluid heights. Finally, the output vector can be defined as y(t) = x(t). Symbolically, {u(t), x(t), y(t)} ∈ ℝ².

The state-space matrices A_ss, B_ss, C_ss, and D_ss are defined for the NIS and IS configurations as follows. The matrices C_ss = I_2×2 and D_ss = 0_2×2 are identical for both configurations. The matrices A_ss, B_ss, C_ss, and D_ss represent the state, input, output, and direct transmission dynamics, respectively. Additionally, $\left\{\mathbf{A}_{\mathrm{ss}}, \mathbf{B}_{\mathrm{ss}}, \mathbf{C}_{\mathrm{ss}}, \mathbf{D}_{\mathrm{ss}}\right\} \in \mathscr{M}_{2 \times 2}$.

3.6.   State-space matrices for NIS and IS

For NIS:

For IS:

The constants K_ij (for {i, j} ∈ {1, 2}) are defined as follows: K₁₁ = 0.5∙C'_v1/sqrt(H₁^ss), K₂₁ = 0.5∙C'_v2/sqrt(H₂^ss), K₁₂ = 0.5∙C'_v1/sqrt(H₁^ss − H₂^ss), and K₂₂ = 0.5∙(C'_v1/sqrt(H₁^ss − H₂^ss) + C'_v2/sqrt(H₂^ss)).

These constants are integral to determining the system's response to perturbations and deviations from the steady state.

The presented dynamic modeling framework provides a comprehensive mathematical representation of the water supply plant's behavior under different configurations. By applying mass conservation principles, nonlinear dynamic models are derived that capture the intricate interactions within the system. The linearized models facilitate control design and analysis, providing insights into system stability and performance under various operating conditions. This approach underscores the importance of precise modeling in optimizing fluid dynamics and control strategies in industrial applications.

4.   Stability analysis

Stability analysis is a crucial aspect of understanding the dynamic behavior of systems, particularly for the NIS and IS configurations. Analyzing the stability involves examining whether a system can return to its steady state after experiencing perturbations, or if it will diverge, indicating instability. This can be assessed by evaluating the characteristic values (λ) of the state-space representations for both systems.

4.1.   State-space representation and characteristic equation

The stability analysis of the NIS and IS involves examining their state-space matrices A_ss derived from (11) and (12). The characteristic equation, which provides insights into the system's stability, is determined by solving the following determinant equation:

Here, A_ss represents the state matrix, specifically defined for NIS and IS in (10) and (11); λ represents the eigenvalues of the matrix A_ss, and I_2×2 is the 2 × 2 identity matrix.

Eigenvalues are crucial indicators of system stability. For a system to be stable, all eigenvalues must possess negative real parts, which ensures the system's natural return to equilibrium post-disturbance ^[20].

4.2.   Eigenvalue calculation for NIS and IS

Solving (12) provides the eigenvalues for both the NIS and the IS, allowing for a detailed stability analysis.

The solution of the (12) for the NIS configuration yields the following eigenvalues:

Similarly, the eigenvalues for the IS configuration are given by:

The constants α_i and β_i (i ∈ {1, 2}) are formulated to incorporate system-specific parameters, which play a pivotal role in the stability assessment. They are defined as follows:

For NIS:

For IS:

where K₁₁, K₂₁, K₁₂, and K₂₂ are predefined system parameters reflecting the characteristics of valves and fluid dynamics within the tanks. Also, A_TK-100 and A_TK-200 denote the cross-sectional areas of tanks TK-100 and TK-200, respectively, which are essential in quantifying hydraulic resistance and flow properties.

4.3.   Analysis of eigenvalues

The obtained eigenvalues from (13) and (14) provide significant insights into system stability:

• Real parts of eigenvalues: Stability is primarily indicated by the sign of the real part of λ. Negative real parts imply that the system will return to equilibrium post-disturbance.

• Imaginary parts of eigenvalues: The presence of imaginary components denotes oscillatory dynamics, with the magnitude determining oscillation frequency.

Upon solving (13) and (14) for both NIS and IS configurations, the eigenvalues λ_ij (for {i, j} ∈ {1, 2}) are determined to be real and negative under the simulation conditions. This result implies that both systems exhibit stable behavior, as they naturally tend to return to their steady state following perturbations. Such negative real eigenvalues confirm the systems' stability under normal operational conditions ^[20,21].

5.   Control system design

In this article, the design and analysis of three controllers are explored for regulating a dynamic process in two distinct configurations: NIS and IS. The first two controllers leverage linear control methodologies: a PI compensator and an LQR. The third controller employs a nonlinear control strategy, specifically a SMC. Each controller is designed to achieve optimal performance within their respective frameworks.

To facilitate the development of these designs, it is essential to have a table that classifies the type of variable related to the linear model defined in (9). Table 1 illustrates a classification by type of signal, as defined in (9), that is necessary for the successful completion of these designs.

From Table 1, it can be explained that ^[17]:

• Inputs: These are the external signals or disturbances fed into the system. For both NIS and IS, the primary inputs are the inlet flow rate f_i(t) and the setpoint h₁^*(t), which dictates the desired tank level in TK-100.

• Outputs: These are the measurable variables of interest. For NIS, the outputs are the tank level h₁(t) and the outlet flow rate f_o(t). In IS, there are additional outputs, including the tank level h₂(t).

• Manipulated variable: This is the parameter controlled by the system to achieve the desired output. In this case, λ_drive(t) is the actuation signal that influences the hydraulic pump, thereby regulating f_o(t).

• Controlled variables: These are the variables that the control system aims to regulate. For both NIS and IS, these include the tank levels h₁(t) and h₂(t) (in IS) and the outlet flow rate f_o(t).

This table summarizes the linear models' key components, focusing on the process dynamics and control objectives for both NIS and IS.

5.1.   Design of a PI compensator

The design of the PI compensator is rooted in the state-space representation provided by (9) and illustrated in Figure 2.

This model is transformed into the Laplace (s) domain under the assumption of zero initial conditions. The resulting s-domain vector representation of the process is given by:

where I is the 2 x 2 identity matrix. Here, Y(s) = [H₁(s), H₂(s)]^T and U(s) = [F_i(s), F_o(s)]^T, with {Y(s), U(s)} ∈ ₵². By using the superposition principle and analyzing (17), the expressions for H₁(s) and H₂(s) for both NIS and IS configurations are derived:

NIS and IS are defined in (18) and (19), respectively. The denominators D₁(s) and D₂(s) are given by

Moreover, the sensor-transmitter and drive dynamics are modeled as first-order systems, given by

It is important to note that the gains k_Ti are considered non-unitary, as the level measurements are typically expressed in percentage terms relative to their maximum operational heights, adhering to ISA standards ^[17].

The closed-loop transfer function for both NIS and IS, incorporating the PI compensator G_c(s) and dynamics H_s(s) and G_drive(s), is represented as:

where G_p(s) = H₁(s)/F_o(s), derived from (18). The PI compensator is designed using a first-order approximation with time delay, resulting in the following transfer function:

Applying the Ziegler-Nichols tuning method ^[17,19], the compensator's tuning parameters are determined by

5.2.   Design of an LQR

The LQR design is based on optimal control theory ^[22]. The system's state equation is expressed as $\dot{\mathbf{x}}\left(t\right) = {\mathbf{A}}_{\mathbf{s}\mathbf{s}}· \mathbf{x}\left(t\right)+{\mathbf{B}}_{\mathbf{s}\mathbf{s}}· \mathbf{u}\left(t\right)$, and the control law u(t) = −K⋅x(t) is implemented to minimize the quadratic cost function:

In this formulation, Q and R are positive definite Hermitian matrices ^[3,4]. By substituting the control law into the state equation, the optimized state-space model is obtained:

The optimal matrix K ensures the stability of the matrix (A_ss − B_ss⋅K), characterized by its eigenvalues having negative real parts.

The equation establishes the connection with the positive definite Hermitian matrix P ^[19]. By solving the time derivative, the continuous-time algebraic Riccati equation is formulated as:

The gain matrix K is subsequently computed using:

This solution stems from the minimization of the cost function J. The LQR is fundamentally a regulator, designed for systems where reference inputs are null ^[3,4]. To accommodate non-zero set points in the proposed process, the state-space model is converted from deviation to absolute variables, as follows:

The state vector x(t) = [h₁(t), h₂(t)]^T and the steady-state vector X^ss = [H₁^ss, H₂^ss]^T describe the system's behavior, with the output vector y(t) = x(t). Moreover, {x(t), X^ss, y(t)} ∈ ℝ². This leads to the control law:

where U^ss = [F_i^ss, F_o^ss]^T. The selection of Q and R matrices significantly influences the LQR's performance, as demonstrated in simulations within MATLAB™/Simulink™ environments. The block diagram of the LQR system for the NIS and the IS is illustrated in Figure 3.

5.3.   Design of an SMC

The nonlinear dynamics of the process, as defined by (5) and (6), are employed to formulate and implement an SMC for both the NIS and the IS. The primary control objective is the regulation of the fluid height h₁(t). The control strategy hinges on minimizing the error in h₁(t), defined as e_h1(t) = h₁^*(t) − h₁(t), where h₁^*(t) denotes the reference height. By incorporating e_h1(t) into the control design, the control laws can be derived, which correspond to the sliding surface. Upon manipulating (5) and (6) to express them in terms of e_h1(t), the control laws are obtained and represented as follows ^[5,6]:

For NIS:

For IS:

These equations are valid for both the NIS and IS systems ^[5]. The parameter β represents the time constant associated with the desired first-order response of the error e_h1(t). The existence of sliding mode operation necessitates that S(e_h1(t), t) = 0 ^[14,18]. To maintain this regime, the control system must ensure that dS(e_h1(t), t)/dt = 0. The actuation signal λ_drive(t) ∈ [0 %, 100 %], generated by the SMC, modulates the flow rate f_o(t) via the hydraulic pump, thereby regulating h₁(t). Although λ_drive(t) is not explicitly present in (6) and (7) (as these are derived from a pure mass balance model without direct control inputs), it must be incorporated into the sliding surface S(e_h1(t), t). This incorporation allows the SMC to modulate λ_drive(t) rapidly, driving the dynamics of h₁(t) to the desired sliding surface S(e_h1(t), t) ^[14,18].

Assuming a properly designed SMC, the steady-state drive signal λ_drive^ss can be approximated by:

For NIS:

For IS:

This approximation applies to both the NIS and IS systems, leading to modified expressions for S(e_h1(t), t). The revised forms of (34) and (35) are as follows:

For NIS:

For IS:

As previously mentioned, the existence of sliding mode operation requires that S(e_h1(t), t) = 0. Moreover, to remain within this regime, the control system must satisfy dS(e_h1(t), t)/dt = 0. Therefore, the switching law λ_drive(t) must ensure the stability of the sliding mode system, as expressed by the inequality:

From (32)−(38), and assuming the expressions (34) and (35) remain constant, the time derivatives of S(e_h1(t), t) for the NIS and IS systems are derived as follows:

For NIS:

For IS:

From (39) and (40), the following analysis can be established: if S(e_h1(t), t) ≥ 0 then dS(e_h1(t), t)/dt < 0, which implies df_o(t)/dt < 0, and thus λ_drive(t) = 0 %. Conversely, if S(e_h1(t), t) < 0, then dS(e_h1(t), t)/dt > 0, which implies df_o(t)/dt > 0, e_h1(t) < 0, and therefore λ_drive(t) = 100 %. Consequently, the switching law λ_drive(t) is defined as follows:

where ∈ [−1, 1].

The block diagram of the SMC is illustrated in Figure 4.

6.   Simulation results

The dynamic behavior of the NIS and IS was evaluated through extensive simulations utilizing the nonlinear models delineated in (6) and (7), implemented in MATLAB Simulink. The process parameters and steady-state variables, as specified in Table 2, were employed for both systems. The weighting matrices Q and R, necessary for the formulation of the LQR controller, were defined as:

All simulations were conducted over a temporal span of 2, 000 s (0.56 h), with the NIS and IS initialized from zero initial conditions. At the start of each simulation, the setpoint h₁^*(t) and the inlet flow rate f_i(t) were initialized to 75% and 30 m³/s, respectively. A step change in f_i(t) was introduced at 500 s (0.138 h), increasing the flow rate to a new steady-state value of 60 m³/s. Another step change occurred at 1, 000 s (0.28 h), where fi(t) was adjusted to its final value of 50 m³/s. Subsequently, at 1, 500 s (0.42 h), a step change in h₁^∗(t) was introduced, resulting in a new steady-state value of 90% for h₁(t). It should be recalled that, in this case, the function f_i(t) acts as a disturbance signal for both models.

As a preliminary analysis, the characterization of the dynamics of h₁(t) and h₂(t) (controlled variables) with respect to their step response can be obtained by leveraging the linear models in (9) for the NIS and IS systems. Figure 5 illustrates the characterization of the controlled variables h₁(t) and h₂(t), which can be observed through the visualization of the rise time, settling time, and steady-state value (final value). Figure 5(a) depicts the NIS, while Figure 5(b) illustrates the IS.

As depicted in Figure 5, the IS demonstrates significantly elevated values across key performance metrics, including rise time, settling time, and steady-state values. This observation indicates that the dynamic coupling between the interconnected tanks within the IS introduces additional complexity to the system's response, effectively decelerating its overall dynamics relative to the NIS. The interaction between the tanks introduces additional poles in the system's transfer function, contributing to slower transient response characteristics and prolonged stabilization times. Consequently, the IS exhibits a more sluggish response when subjected to perturbations, underscoring the impact of dynamic coupling on the system's temporal behavior. Table 3 summarizes the values of these metrics by system.

To thoroughly assess the performance of the three controllers applied to the NIS and IS, four distinct practical scenarios have been defined, each corresponding to a specific controller configuration. Cases 1, 2, and 3 pertain to the implementation of PI, LQR, and SMC controllers, respectively. The fourth scenario involves the application of the PI controller to the nonlinear plant, which is modeled by (6) and (7).

Figures 6(a) and (b), alongside Figures 8(a) and (b), present the simulation outcomes for Cases 1 and 2, focusing on the NIS and IS. The critical variables under analysis include the height and its corresponding reference value of the TK-100 [denoted as h₁(t) and h₁^*(t)], the height of the TK-200 [denoted as h₂(t) and h₂^*(t)], the inlet flow rate [denoted as f_i(t)], and the regulated outlet flow rate [denoted as f_o(t)].

Conversely, Figures 7(a) and (b), as well as Figures 9(a) and (b), illustrate the simulation results for Cases 3 and 4, also in relation to both the NIS and IS. These figures provide a comprehensive comparison of the system dynamics under different control strategies.

An in-depth analysis of Figures 6−9 culminates in the construction of Table 4. This table encapsulates the calculated figures of merit (FoMs) as delineated in Section 1, for each case and system. The FoMs are presented as a function of the perturbations induced by changes in f_i(t) and h₁^*(t), offering a rigorous evaluation of the control strategies' effectiveness under varying operational conditions.

Based on the analysis of Figures 6−9 and the data presented in Table 4, it becomes evident that the FoMs demonstrate consistent values for both NIS and IS at the initial conditions and during perturbations in h₁^∗(t). The level control maintains precise regulation across all cases, achieving negligible steady-state errors (SE). However, Cases 1 and 4 exhibit significantly higher overshoot (OS) compared to Cases 2 and 3. Notably, in Case 4, the OS exceeds 20%, which is particularly large for this type of process.

Case 2 delivers the most optimal performance, with all FoMs registering zero values except for the settling time (ST), which, while present, is minimal. Case 3, on the other hand, presents a more gradual OS, with the maximum observed at 0.138 h due to perturbations in f_i(t). This case also shows the longest ST, indicating the slowest dynamic response among the scenarios. Additionally, Case 3 exhibits a low-frequency ripple in the outlet flow rate f_o(t) at approximately 14 Hz, caused by the switching surface's influence on the driver actuation signal. This ripple effect propagates to f_o(t), potentially leading to mechanical stress on the system components, such as pipes and fittings.

Table 4, detailing the FoMs for h₁(t) in each case, corroborates these observations. The results show that Case 2 consistently outperforms the others, particularly in minimizing OS and ST. In contrast, Case 4, while maintaining negligible SE, shows the highest OS values, indicating a suboptimal response when a linear compensator is applied to the nonlinear plant.

On the other hand, nonlinear controllers play a crucial role in reducing errors in systems with complex dynamics, offering significant advantages over linear controllers ^[23]. As demonstrated in the article, nonlinear controllers, such as SMC, are better suited to manage the complexities inherent in systems with nonlinear characteristics. In the simulations conducted on both the NIS and IS, it was evident that the dynamic coupling in the IS introduced additional poles in the system's transfer function, leading to slower rise times, extended STs, and altered SE. Linear controllers, such as PI and LQR, often struggle to compensate for these complexities, resulting in significant OS and prolonged ST, particularly in the IS. Conversely, nonlinear controllers are specifically designed to address these dynamics, reducing OS and improving ST by directly managing the nonlinearities in the system.

The robustness of nonlinear controllers under disturbances is another key advantage. This work discusses the introduction of disturbances through step changes in the inlet flow rate [f_i(t)] and the reference height [h₁^*(t)]. In these scenarios, the nonlinear SMC controller demonstrated its ability to maintain control performance, albeit with a low-frequency ripple in the outlet flow rate [f_o(t)] due to the switching surface effect. While this ripple is a byproduct of the SMC's design, it did not significantly compromise the overall stability of the system. In contrast, linear controllers, particularly in the case where a PI controller was applied to the nonlinear plant, exhibited a much larger overshoot, indicating a lack of robustness when dealing with such perturbations.

Moreover, nonlinear controllers have shown a superior ability to minimize SE and improve transient response, particularly in systems where linear controllers may underperform. While the LQR controller in the simulations displayed excellent performance among the linear controllers, achieving zero SE and minimal ST, it still could not outperform the nonlinear SMC controller when it came to effectively managing nonlinearities. The SMC controller maintained system stability and controlled the dynamic response effectively, demonstrating the capability of nonlinear controllers to reduce steady-state errors and manage complex transient dynamics.

Additionally, this paper highlights the enhanced system performance provided by nonlinear controllers in complex coupled systems. The IS, with its interconnected tanks, exhibited more sluggish responses due to the dynamic coupling effects, which posed a challenge for linear controllers. The SMC controller, although introducing a slower ST, provided a controlled and predictable response, avoiding the excessive overshoot observed with the PI controller applied to the nonlinear plant.

In summary, across both NIS and IS, the dynamics of the variables illustrated in Figures 6−9 indicate that the systems maintain stability under the process disturbances. The h₁(t) level control performs optimally in Case 2, while Case 4, despite minimal SE, demonstrates the poorest control performance. This outcome aligns with expectations, given the challenges of applying a linear controller to a nonlinear system. Finally, the implementation of SMC in Case 3 introduces a switched behavior in f_o(t), which could pose risks to mechanical components, including valves, pipes, and fittings, due to the associated ripple effects.

7.   Conclusions

This study has conducted an analysis of the dynamic performance of linear and nonlinear controllers applied to a nonlinear process in both non-interactive and interactive systems. The research journey began with the detailed mathematical modeling of the process, capturing essential dynamics such as fluid levels and flow rates in tanks, which were then represented in a state-space form. This modeling revealed critical insights into the system's stability and controllability, particularly highlighting the impact of nonlinearity, especially in interactive systems, where strong coupling effects between tanks posed significant challenges to control design. These nonlinear interactions were quantified, demonstrating the potential limitations of traditional linear control methods in addressing the complex dynamics present.

In the design of controllers, the proportional-integral compensator, linear quadratic regulator, and sliding mode controller were implemented and evaluated. The proportional-integral controller, designed using the Ziegler-Nichols tuning method, proved to be a straightforward but limited control strategy. While it performed adequately in the non-interactive system, its effectiveness diminished in the interactive system due to the increased complexity and interactions within the system. It required significant tuning and showed limitations in handling model nonlinearities and disturbances. On the other hand, the linear quadratic regulator, grounded in optimal control theory, offered a more robust framework for managing state feedback. In the non-interactive system, it demonstrated commendable performance with fast response and minimal overshoot. However, in the interactive system, the linear quadratic regulator's effectiveness was compromised by the complexity of the required state-feedback gain matrix, its sensitivity to inaccuracies in the system model, and the choice of weighting matrices.

The sliding-mode controller, leveraging its robust nonlinear control approach, excelled in both the non-interactive and interactive systems. It effectively mitigated the adverse effects of nonlinearity and interaction, maintaining stability and ensuring swift convergence to the desired setpoints. The controller's inherent robustness to disturbances and model uncertainties marked it as the superior control strategy, although this came at the cost of a slightly higher control effort due to its switching mechanism. Performance evaluation across the non-interactive and interactive systems highlighted the varying effectiveness of these controllers. In the non-interactive system, the proportional-integral controller struggled with inherent nonlinearities, leading to longer settling times and notable steady-state errors. The linear quadratic regulator offered improved transient response with reduced overshoot and faster settling times, though it was sensitive to model variations. The sliding-mode controller provided the best performance, with rapid response, minimal steady-state error, and resilience to disturbances, proving its suitability for controlling nonlinear systems.

In the interactive system, the increased complexity amplified the challenges faced by linear controllers. The proportional-integral controller exhibited significant overshoot and prolonged settling times, particularly due to the interactive effects between system variables. The linear quadratic regulator, while outperforming the proportional-integral controller, still faced constraints due to the interactive nature of the system and showed sensitivity to the tuning of the weighting matrices. Conversely, the sliding-mode controller demonstrated superior performance, managing the interactions with ease, and maintaining high accuracy and stability. Its robustness was particularly evident in the face of model uncertainties and disturbances, confirming its status as the most effective controller for the interactive system.

The study also provided key technical insights for future work. The robustness of the sliding-mode controller stands out as a pivotal finding, indicating that nonlinear control strategies are better suited for complex, interactive processes. The controller's ability to manage both structured and unstructured uncertainties underscores its potential in practical applications where model precision is often a challenge. The comparison between linear and nonlinear control methods highlighted the limitations of linear approaches like proportional-integral controller and linear quadratic regulator in dealing with nonlinear dynamics and interactive effects. While the linear quadratic regulator offers a more sophisticated approach than the proportional-integral controller, it remains inherently constrained by its reliance on linear approximations of the system model, advocating for the consideration of nonlinear control methods like sliding-mode controller in similar applications.

Another important consideration is the control effort and energy consumption, where the sliding-mode controller required higher effort due to its switching nature. However, this trade-off is justified by its superior control performance. Future research could explore optimizing the sliding-mode controller to reduce control effort without compromising its robustness, potentially through adaptive sliding-mode techniques or hybrid control strategies. Additionally, given the challenges identified with both linear and nonlinear controllers, future work could investigate adaptive control strategies that dynamically adjust controller parameters in real time based on system performance. Hybrid control strategies that combine the strengths of linear and nonlinear controllers could also be explored to optimize performance across a broader range of operating conditions.

Practical implementation considerations are also crucial. While the simulation results provide a solid foundation, real-world implementation would require addressing challenges such as sensor noise, actuator limitations, and computational constraints. Experimental validation of the controllers on a physical system would be a logical next step, providing insights into the practical challenges and refining the control strategies accordingly. In summary, this study establishes that while linear controllers like proportional-integral and linear quadratic regulator can be effective in simple, non-interactive systems, they are outperformed by nonlinear strategies like the sliding-mode controller in complex, interactive systems. The sliding-mode controller's robustness, adaptability, and superior performance make it the preferred choice for controlling nonlinear processes.

Author contributions

José M. Campos-Salazar: conceptualization, software, investigation, methodology, validation, writing ‒ original draft, writing ‒ review & editing; Pablo Lecaros: conceptualization, writing ‒ original draft, writing ‒ review & editing; Rodrigo Sandoval-García: conceptualization, writing ‒ original draft, writing ‒ review & editing. All authors have read and agreed to the published version of the manuscript.

Conflict of interest

The authors declare that there is no conflict of interest in this paper.