BESS based voltage stability improvement enhancing the optimal control of real and reactive power compensation

1.   Research and development of optimization control algorithms

1.1.   Origin and development of optimal control design

The research on optimal control for nonlinear systems plays a significant role in industry and military fields. Due to the influence of the environment and the limitations of the engineering system, it is very tough to maximize or minimize the performance index of the controlled system in practical. Therefore, optimization problem is a difficult problem in current control field, and has gradually been the focus of attention. The optimal control problems of nonlinear systems are finally transformed into the solutions of Hamilton-Jacobi-Bellman (HJB) partial differential equations.

However, because the HJB equation is a nonlinear partial differential equation, it is difficult to obtain an analytical solution. Therefore, how to obtain the analytical solution of HJB equation then realize the optimization performance index of the system, is the key points to resolve the optimization issue.

In order to avoid the problems encountered in solving HJB equation, Kalman ^[1] proposed the inverse-optimal-based control method for the first time. On the basis of ^[1], Freeman and Kokotovic ^[2] studied inverse optimization control of nonlinear systems. The basic idea of inverse optimization control is not to minimize the cost function by designing the controller, but to minimize the cost function by designing the appropriate control Lyapunov function(CLF). Therefore, the solution of HJB equation comes down to seeking the CLF of the controlled system, thus avoiding the shortcoming of directly solving HJB equation.

Besides, aiming at the above problems, Bellman ^[3] proposed the theory of dynamic programming (DP). However, the issue of "dimension disaster" would be caused in the process of DP control design, that is, the complexity of space storage and computation increases exponentially with the increase of the dimension of control vectors and states. Therefore, in order to overcome the phenomenon of "dimension disaster" in the process of optimal control design, an adaptive optimal control design method combining NNs is proposed by Werbos ^[4], which is called RL or adaptive/ approximate dynamic programming (ADP). In the control field, RL can effectively solve the "dimension disaster" problem in DP. In ^[5], Werbos retrospected the classic econometric approach and proposed a robust method. In ^[6], Werbos defined a more limited design called "brain-like intelligent control", it discusses the brain as a member of intelligent control, which implies a property to be sought in future research.

1.2.   Development of optimization control algorithms

Since then, inspired by ^[4], large amounts of optimal control methods via APD have been developed, see ^[7,8]. Among them, for continuous-time (CT) systems, in offline situations, Abu-Khalaf and Lewis ^[9] presented an offline algorithm via RL to solve the optimal control issue of CT nonlinear systems. Since the offline control algorithms cannot be adopted to adjust online in real time, thus, to overcome this disadvantage, Vamvoudak and Lewis ^[10] proposed an online adaptive method via policy iteration. In ^[11], Li et al. investigated the Lyapunov stability problem for impulsive systems via event-triggered impulsive control. In ^[12], Li et al. considerd a class of nonlinear impulsive systems with delayed impulses, based on impulsive control theory and the ideas of average dwell-time (ADT), a set of Lyapunov-based sufficient conditions for globally exponential stability were obtained. However, we need to know the accurate knowledge of CT nonlinear systems in ^[9,10]. Since nonlinear systems usually contain uncertain nonlinear functions, it it difficult to acquire the analytical solution of the HJB equation.

In order to solve this problem, by choosing an appropriate cost function to reflect uncertainty regulation, the authors in ^[13] proposed a robust optimization controller design strategy based on an online strategy iterative algorithm for a class of continuous nonlinear systems with nonlinearities. Zhang et al. ^[14] designed a new data-driven robust identified optimization tracking controller via the acquired data-driven model for a kind of nonlinear CT systems.

2.   Development of the adaptive optimal control for affine nonlinear systems

2.1.   Design of optimal control for affine nonlinear systems

Consider a class of affine nonlinear system as:

where $f(x)$ and $g(x)$ are the uncertain smooth functions, which satisfy that $f(0) = 0$, $g(0) = 0$. $u$ is the control input, $x\in \textbf{R}^{n}$ is the state vector. For the above system, some adaptive optimization control strategies have been proposed.

In ^[15], for a class of affine nonlinear CT systems with unknown internal dynamics, Liu and Wang et al. developed an online method based on ADP, which constructed a critic neural network to facilitate the solution of the modified HJB equation. In ^[16], Liu et al. developed an online optimization control algorithm for CT affine nonlinear systems with infinite horizon cost. And in ^[17], Wen and Chen et al. studied an adaptive optimized tracking control method via RL algorithm and NNs.

For ^[16,17], value function is selected as:

where $r(z, u) = z^{T}(t)Q(x)z(t) + u^{T}u$ is the value function, and $Q(x) = q(x)q^{T}(x)\in \textbf{R}^{n\times n}$ is a positive definite matrix. The HJB equation is defined as:

where $V_{z}\in \textbf{R}^{n}$ is the partial gradient of $V_{z}$, $y_{d}(t)\in \textbf{R}_{n}$ is the ideal tracking trajectory, $z(t) = x(t)-y_{d}(t)$ is the tracking error. When considering the input constraint control and saturation constraints control issue, Liu and Yang developed a robust optimal adaptive optimal control method via RL for a kind of uncertain nonlinear systems. In ^[18,19], there exists a symmetric definite matrix $Q$, and the value function is selected as:

where $\varpi(u)$ is positive. For the sake of solving the constraint control issue, define $\varpi(u)$ as:

where $R = diag[r_{1}, \cdots, r_{n}]$ with $r_{i} > 0$, $(i = 1, \cdots, m)$, $\psi(\cdot)$ is a bounded one-to-one function with $|\psi(\cdot)|\leq1$, $\psi\in \textbf{R}^{m}$, $\psi^{-1} = (\psi^{-1})^{T}$, $\psi^{-1}(\upsilon/\kappa) = [\psi^{-1}(\upsilon_{1}/\kappa), \cdots, \psi^{-1}(\upsilon_{m}/\kappa)]^{T}$, $u(x)\in \Xi$, $\Xi = \{{u|u\in \textbf{R}^{m}, |u_{i}|\leq \kappa, i = 1, 2, \cdots, m}\}$, $\kappa > 0$ is a constant. Define the HJB equation and the value function as:

where $V_{x}\in \textbf{R}^{n}$ is the partial derivative of $V(x)$ with respect to $x$.

In the previous article, since there exist the unknown nonlinear functions $f(x)$ and $g(x)$, the analytic solution of the equation cannot be received when resolving the HJB equation. Because of their properties and fault tolerance, attributes of nonlinearity, adaptivity, the identified solution of the HJB equation can be obtained symmetric via NNs.

2.2.   Development of identifier-actor-critic-based optimization control

Because the system (2.1) contains unknown dynamics, we can identify the system for receiving the optimal control. In ^[20], Yang et al. presented identifier-actor-critic (IAC) structure, where the actor NN is carried out control actions, and critic NN is employed to estimated these actions, and then returns the evaluations to actor, and the dynamics of uncertain system robust dynamic can be approximate by NN identifiers. From system (2.1), we have that:

where $A\in \textbf {R}^{n\times n}$ is a certain constant matrix, $\digamma(x) = f(x)-Ax$.

A NN is applied to identify $\digamma(x)$ as follows:

where $\varepsilon_{1}(x)\in \textbf {R}^{n}$ is the NN function reestablishment error, $\sigma(x)$ is the activation function, $W_{1}^{T}\in \textbf {R}^{n\times n}$ is the NN weight. By using (2.8), (2.7) can be developed by:

The NN identifier is designed as:

where $\hat{x}\in \textbf{R}^{n}$ is the identifier NN state, $\hat{W}_{1}\in \textbf{R}^{n\times n}$ is weight estimation, and $v(t)$ is the robust feedback term.

The optimal value function can be expressed by NN as:

The optimal control can be expressed by NN as:

where $\varepsilon_{v}(\cdot)\in R$ is the function reestablishment error, $\phi(\hat{x}) = [\phi_{1}(\hat{x}), \phi_{2}(\hat{x}), \cdots, \phi_{N}(\hat{x})]^{T}\in \textbf{R}^{N}$, $\phi'(\hat{x}) = \frac{\bigtriangleup \partial \phi(\hat{x})}{\partial \hat{x}}$ and $W\in \textbf{R}^{N}$ are uncertain desired NN weights, $N$ is the number of neurons.

The critic-actor $\hat{V}(\hat{x})$ and $\hat{u}$, which can learn the optimization value function and adjust the optimization control online, is expressed as:

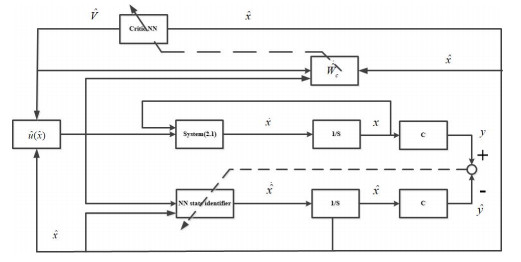
where $\hat{W}_{c}(t)\in \textbf{R}^{N}$ and $\hat{W}_{a}(t)\in \textbf{R}^{N}$ estimate the ideal weights of the critic-actor NNs. Whereas the system dynamics are estimated online by using the identification error $\tilde{x}(t) = x(t)-\hat{x}(t)$. The overall planning diagram of the control algorithm is given in Figure 1.

Besides Bhasin et al. ^[21] proposed an online adaptive solution via RL for the unbounded optimization control nonlinear systems with CT uncertain problem. The advantage of using the IAC structure is that the learning of critics, actors, and identifiers is successive and simultaneous, removing the knowledge of system drift dynamics.

However, the above proposed control design algorithm for the affine nonlinear systems cannot be used to solve the optimal control issues for unmatching condition nonlinear systems, because it cannot guarantee the optimization of each subsystem.

3.   Adaptive optimization control based on backstepping for strict nonlinear systems

3.1.   Design of optimization control based on backstepping for strict feedback nonlinear systems

The above research methods on affine nonlinear systems cannot be applied to nonlinear systems with unmatching conditions and the optimality of each subsystem can not be guaranteed. In order to solve the problem of unmatching conditions, we used the backstepping technology, which can also optimize each subsystem.

Consider the following strict feedback nonlinear systems as:

where $u$ and $y$ are the control input and output, $x$ is the state, $\bar{x_{i}} = [x_{1}, x_{2}, \cdots, x_{i}]$, is the system state vector. $f_{i}(\cdot)$ is the uncertain nonlinear function, which satisfies $f(0) = 0$.

In 1995, Kristic ^[22] firstly proposed the backstepping technology. The design idea of the backstepping algorithm is as follows: for systems that satisfy strict feedback control structures, via the backstepping algorithm, the Lyapunov function and controller are constructed in a systematic way. Then, for each subsystem, local Lyapunov function and intermediate control function are designed successively until the design of the whole controller is completed.

For the sake of solving the control issue for unmatching nonlinear systems (3.1), Wen et al. ^[23] first proposed an optimized backstepping control technology, under the backstepping framework, we can ensure that each subsystem can be optimized. Based on ^[23], for a kind of nonlinear large-scale systems with strict-feedback structure, Tong et al. ^[24] proposed the fuzzy decentralized adaptive optimal control, and used FLS to identify the uncertain nonlinear function of the systems. And in ^[25], for a quarter of the car active electric suspension systems, Li et al. addressed the output-feedback adaptive NN optimization control issue.

Because there are unknown nonlinear functions, the updating laws and learning laws designed for the above systems are very complex. In order to solve this problem, in ^[26], Wen et al. proposed a simplified RL algorithm, which generates a negative gradient of a simple positive function from the partial derivative of HJB equation, and derives a new law from the negative gradient.

Define the Hamiltonian's approximation error as:

where $V_{\hat{z}}^{*}(\hat{z})$ is the gradient of $V^{*}(\hat{z})$, $u^{*}$ is the optimal control. Since $V_{\hat{z}}^{*}(\hat{z})$ and $u^{*}$ contain the unknown part $V_{\hat{z}}^{0}(\hat{z})$, which can be approximated on a compact set by NNs as:

Since $\Theta_{V}^{*}$ is an uncertain constant vector, it is not available in practical control, RL algorithm is implemented by both critic-actor NNs.

The learning law of critic NN is designed as:

where $k_{c}$ is the critic network learning rate, $\hat{\Theta}_{Vc}(t)$ is the critic NN weight.

The learning law of actor NN is designed as:

where $k_{a}$ is the actor network learning rate, $\hat{\Theta}_{Va}(t)$ is the actor NN weight, $k_{a} > k_{c} > 0$.

In accordance with the above description, the optimal solution ${{\hat{\alpha}}}(\hat{z})$ is supposed to meet $E(t) = H(\hat{z}, u, \hat{V}_{\hat{z}}^{*})\rightarrow 0$.

If $H(\hat{z}, u, \hat{V}_{\hat{z}}^{*})$ is held and exist the unique solution, then it is equivalent to the following equation holds:

The positive definite function is designed as:

Clearly, the Eq (3.6) is the equivalent to $P(t) = 0$. Since $\frac{\partial P(t)}{\partial \hat{\Theta}_{Va}(t)} = -\frac{\partial P(t)}{{\partial \hat{\Theta}_{Vc}}(t)} = 2(\hat{\Theta}_{Va}(t)-\hat{\Theta}_{Vc}(t))$, we can get

In ^[27], for nonlinear lithium battery systems, Pei et al. addressed adaptive NN output feedback optimization control problem, and the stability of the nonlinear lithium battery is proved.

On the basis of ^[26], under the frame of backstepping control, some simplified-based adaptive optimization control algorithms have been proposed, which require construct all intermediate control functions and the actual control function of backstepping to be the optimization controls, hence, RL is performed in each subsystem (see Figure 2).

In ^[28], Wen et al. addressed optimization control method for nonlinear strict-feedback systems with unknown functions. In ^[29], for second-order unknown nonlinear multiagent systems, Lan et al. proposed a distributed time-varying optimization formation protocol based on an adaptive NN state observer. In ^[30], Xiao et al. addressed the distributed optimization containment control issue for multiple nonholonomic mobile robots differential game.

3.2.   State-constrained optimal control based on backstepping

It is worth mentioning that system states usually need to be confined within some preselected compact sets due to the physical limitations of actual systems. For real systems, in ^[31], Jiang and Lou considered the input-to-state stability (ISS) of delayed systems with bounded-delay impulses. In ^[32], for a hydraulic servo actuator (HSA) with sensor faults, Vladimir and Ljubisa investigated the mechanism for the fault estimation (FE) problem. However, methods in ^[29,30] could not solve the actual constraint problem. To solve this problem, various state-constrained control methodologies is discussed.

Aiming at strict-feedback nonlinear systems, which contain immeasurable states and internal dynamics, Li et al. ^[33] proposed an output-feedback adaptive NN optimization control design. Under the backstepping control design, there will be coupling terms or cross terms at each step, which will lead to that each subsystem is not optimal. Therefore, state constraints should be introduced to make the coupling terms bounded to ensure that each subsystem is optimal. And all the states are limited in the compact sets, that is, $|x_{i}| < k_{ci}$, where $k_{ci} > 0$.

The neoteric barrier optimization performance index functions for subsystems are designed to ensure that the system state does not violate the constraint bounds and achieves the optimization control objective, which is selected as:

where $\tau$ is the terminal time, $q(z, \alpha) = \xi log[k_{b}^{4}/(k_{b}^{4}-z^{4})]+r(\alpha)^{2}$, $\xi > 0$ is a constant, $\alpha$ is the intermediate control function, The following Hamiltonian can be derived as:

According to the algorithm presented in ^[34], for power systems with stochastic character, Li et al. designed the adaptive NN optimal tracking control to resolve the issue of state constraints and uncertain nonlinear dynamics. In ^[35], Li et al. put forward an adaptive NN optimized output-feedback control method to solve the issue of unknown nonlinear dynamics and input saturation. In ^[36], for uncertain nonlinear systems with time-varying full state constraints, input saturation and unknown control direction, Wu and Xie employed asymmetric barrier Lyapunov functions, the auxiliary subsystem and the Nussbaum gain technique.

Based on the above published works, some adaptive optimal control methods via backstepping control have also been applied to practical systems, for example, see ^[37,38]. In ^[37], Li et al. presented an adaptive NN optimized control strategy for full vehicle active suspension system. And in ^[38], Li et al. studied adaptive optimal formation control approach for second-order stochastic multi-agent system, which contains unknown nonlinear dynamics.

3.3.   Inverse optimization control based on backstepping

Based on the inverse optimization control method in ^[1], Ezal et al. ^[38] proposed a new robust backstepping inverse optimal control design, which achieved both local optimization and global inverse optimization. For a class of nonlinear uncertain strict feedback systems, Li et al. ^[39] designed adaptive fuzzy inverse optimization control by establishing an equivalent system and an auxiliary system.

System (2.1) can be rewritten as the following nonlinear system:

where $u\in \textbf{R}$ is the control input, $x$ is the state vector, $x = 0$ is the equilibrium point of system. $q(x)$ is an uncertain bounded function vector, $G(x)$ and $F(x)$ are smooth function vectors.

Define $\gamma$ is a class $K_{\infty}$ function, then the derivative of $\gamma$ exists and it is also a class $K_{\infty}$ function. An auxiliary system is constructed for the nonlinear system (2.1):

where $V(x)$ is the control Lyapunov function. $L\vartriangle V = \partial\vartriangle V/\partial x$, $L_{F}V_{n} = \partial V_{n}/\partial xF(x)$, $L_{G}V_{n} = \partial V_{n}/\partial xG(x)$.

The cost functional is selected as:

where $D$ is a set of locally bounded functions of $x$, $R(x)$ is matrix-valued function, which satisfied that $R(x) = R(x)^{T} > 0$. $E(x)$ and $l(x)$ are positive definite radially unbounded functions.

The fuzzy adaptive inverse optimization control structure is shown in Figure 3.

And in ^[40], Li et al. studied a fuzzy inverse optimization fuzzy adaptive output feedback control method based on observer for a class of nonlinear strict feedback systems. In ^[41], Lu et al. addressed a fuzzy adaptive inverse optimization control issue, and a switching inverse optimization controller is constructed by using a single parameter learning mechanism, which confirmed that the method guarantees the input-to-state stability of the control systems.

Inspired by the above theory, the inverse optimization theory is also widely applied to some practical systems. In ^[42], for vehicle active suspension system with unknown nonlinear dynamics, Li et al. designed an adaptive fuzzy inverse optimal control method via state observer. Long et al. ^[43] proposed an inverse optimal fuzzy adaptive control approach for the system of flexible spacecraft system with fault-free actuator, which is subjected to input saturation, uncertain parameter and external disturbances.

In addition, people hope the practical engineering will reach the stable in finite time, and use the less control energy when achieving the satisfactory performance indicators simultaneously. Thus, how to achieve the effective balance between control quality and control energy has become a hot research issue. In ^[44], for nonlinear impulsive systems, Li and Ho studied the problem of finite-time stability (FTS). In ^[45], Li and Yang developed the Lyapunov–Razumikhin method for finite-time stability (FTS) and finite-time contractive stability (FTCS) of time-delay systems. In ^[46], via the power integral control approach and backstepping control method, Yang designed a semi-global real finite time controller. Then, according to the basic idea of inverse optimization, an appropriate objective functional is constructed, and the constructed objective functional is minimized by adjusting the parameters of semi-global real finite time controller.

Consider the Lyapunov function as follows:

where $\bar{\omega_{1}} = \omega_{1}^{*}-\hat{\omega_{1}}$, $\hat{\omega_{1}}$ is the estimation of the unknown parameter $\omega_{1}^{*}$, $v = max\{{r_{1}, p_{1}r_{2}}\}$, $j = 1, 2, \cdots, n$, $p_{j}r_{j+1} = r_{j}+\tau$, $\upsilon = \mathop{max}\limits_{1\leq j\leq n} \{r_{j}, p_{j}r_{j+1}\}$, $j = 1, 2, \cdots, n$. $r_{j}$ and $p_{j}$ is the ratio of two positive odd numbers. $r_{1} = 1$, $\tau$ is the design parameter.

Based on ^[46], for a class of interlinked nonlinear systems with powers of positive odd rational numbers, Li et al. ^[47] developed a series of homogeneous controllers, which are capable of guaranteeing the local finite-time stability of the closed-loop systems by using the adding one power integrator approach and backstepping technique.

Most of the existing optimization finite-time control methods are limited by complicated design and updating process, which vastly affect the ideal property of optimization finite-time control. In order to solve this issue, in ^[48], Lu et al. first proposed an immediate fuzzy adaptive inverse optimization approach to receive a switching-type inverse optimization controller and a one parameter learning mechanism. The inverse optimal stabilization is solvable, and there exists a matrix-valued function $P(x)$, which satisfied that $P(x) = P(x)^{T} > 0$, then the cost function is defined as:

where $\hbar$ and its derivative $\hbar'$ are $K_{\infty}$ functions, $L(x)$ is positive functions, $u(x)$ is away from the origin in succession with $u(x) = 0$.

For a kind of robotic manipulator system, which contains uncertain dynamics and input saturation, the authors in ^[49] proposed a fixed-time trajectory tracking control approach based on RL. For the sake of guaranteeing that $e_{1}$ and $e_{2}$ convergence to diminutive neighborhood around $0$ in a uniformly bounded convergence time $T_{s}$, where $T_{s}$ stands alone with the original states. A noval nonsingular fixed-time fast terminal sliding mode is proposed as:

where $Ke_{1} = diag[{k_{e11}, k_{e12}, \cdots, k_{e1n}}]$ is a diagonal matrix. $k_{e1i}, i = 1, 2, \cdots, n$, are designed as:

where $p$ and $g$ are positive scalars with $gk > 1$ and $1/\upsilon_{1} < pk < 1$, $\alpha > 0$, $\beta > 0$, $k > 1$, $\upsilon_{1} > 1$.

Obviously, the above developed control method can effectively solve the finite/fixed-time optimal control problems and can make the minimize the cost function. Besides, in ^[50], Hu et al. considered the fixed-time stability of delayed neural networks with impulsive perturbations.

4.   Conclusions

It can be seen from this review that optimization control design for unknown nonlinear systems via RL and ADP has been diffusely studied in control area and has achieved fruitful results. The origin and the development of optimization algorithms have been introduced, the research results of optimization control of affine nonlinear systems have been summarized. Then, under the frame of backstepping control, the adaptive optimal control, finite-time inverse optimal control, constraint control have also been described for strict-feedback nonlinear systems. At the same time, we have summarized the applications development of adaptive optimization control methods. In addition, as a novel hot issue in this field, finite/fixed-time optimal control via backstepping and RL/ADP for nonlinear systems have attracted considerable attentions, both theory and practical applications also need to be further studied in the future.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant No. 61822307.

Conflict of interest

The authors declare there is no conflict of interest.