Citation: Malhar Padhee, Rajesh Karki. Bulk system reliability impacts of forced wind energy curtailment[J]. AIMS Energy, 2018, 6(3): 505-520. doi: 10.3934/energy.2018.3.505
| [1] | Solomon A. A., Michel Child, Upeksha Caldera, Christian Breyer . Exploiting wind-solar resource complementarity to reduce energy storage need. AIMS Energy, 2020, 8(5): 749-770. doi: 10.3934/energy.2020.5.749 |
| [2] | Rashid Al Badwawi, Mohammad Abusara, Tapas Mallick . Speed control of synchronous machine by changing duty cycle of DC/DC buck converter. AIMS Energy, 2015, 3(4): 728-739. doi: 10.3934/energy.2015.4.728 |
| [3] | Jiashen Teh, Ching-Ming Lai, Yu-Huei Cheng . Composite reliability evaluation for transmission network planning. AIMS Energy, 2018, 6(1): 170-186. doi: 10.3934/energy.2018.1.170 |
| [4] | Mulualem T. Yeshalem, Baseem Khan . Design of an off-grid hybrid PV/wind power system for remote mobile base station: A case study. AIMS Energy, 2017, 5(1): 96-112. doi: 10.3934/energy.2017.1.96 |
| [5] | Azevedo Joaquim, Mendonça Fábio . Small scale wind energy harvesting with maximum power tracking. AIMS Energy, 2015, 2(3): 297-315. doi: 10.3934/energy.2015.3.297 |
| [6] | Elio Chiodo, Pasquale De Falco, Luigi Pio Di Noia, Fabio Mottola . Inverse Log-logistic distribution for Extreme Wind Speed modeling: Genesis, identification and Bayes estimation. AIMS Energy, 2018, 6(6): 926-948. doi: 10.3934/energy.2018.6.926 |
| [7] | Nadwan Majeed Ali, Handri Ammari . Design of a hybrid wind-solar street lighting system to power LED lights on highway poles. AIMS Energy, 2022, 10(2): 177-190. doi: 10.3934/energy.2022010 |
| [8] | Ladislas Mutunda Kangaji, Atanda Raji, Efe Orumwense . Cutting-edge progress in offshore wind and tidal stream power technology—State-of-the-Art. AIMS Energy, 2025, 13(1): 188-230. doi: 10.3934/energy.2025007 |
| [9] | S. Vinoth John Prakash, P.K. Dhal . Cost optimization and optimal sizing of standalone biomass/diesel generator/wind turbine/solar microgrid system. AIMS Energy, 2022, 10(4): 665-694. doi: 10.3934/energy.2022032 |
| [10] | Navid Majdi Nasab, Jeff Kilby, Leila Bakhtiaryfard . Integration of wind and tidal turbines using spar buoy floating foundations. AIMS Energy, 2022, 10(6): 1165-1189. doi: 10.3934/energy.2022055 |
The utilization of conventional energy resources such as coal and fossil fuel-based resources cause environmental problems such as the greenhouse gas emissions and acid rain. Wind has become a promising alternative and is being recognized as an important energy source to offset the harmful emissions from conventional energy resources. The gradual reduction in fossil fuel reserves and rapid increase in the energy demands leading to increased societal value of wind power has resulted in considerable amount of investment in wind power technology. As a result, there has been a substantial increase in the global installed wind capacity.
As wind penetration increases to relatively large scales, it becomes important in power system planning to assess the capacity value and reliability impacts of wind resources, as well as the economic and environmental benefits from renewable energy utilization. Wind farms are generally at the top of the priority loading order, and are first dispatched to serve the load. In past scenarios where wind penetration was relatively low, all the wind energy generated were absorbed and utilized by the system. In high wind penetration scenario, however, wind energy available from a wind farm is occasionally spilled or curtailed due to the limitations in operating reserve or ramping capability of the scheduled generating units [1] and transfer capability of transmission lines [2].
References [1,2,3,4,5] analyse the various factors affecting wind power curtailment in large scale power systems. The system reliability and the wind energy benefits can be significantly reduced with the increase in wind energy spillage as there will be less energy available to the system to serve the load. Wind models developed for reliability evaluation should therefore incorporate forced wind energy curtailment. In order to develop such a wind model, important factors such as the system load level, priority loading order of the generating unit and the response rate of the generating units should be considered. References [1] and [4,5,6,7] have considered some of these important factors to quantify the wind energy curtailment in power systems. However, the incorporation of these factors in the adequacy assessment [8] of wind integrated power systems has not been considered. Other transmission related factors, such as, the wind farm interconnection location in the network, overall network configuration, line transfer capability, and capacity of the wind resource and its variability should also be incorporated in the evaluation model. Such models suited to bulk power system adequacy evaluation will be very useful to system planners in assessing the impact of wind farms on bulk system reliability, and on the economic and environmental benefits from wind energy as existing methods do not incorporate forced wind power curtailment due to these factors.
Some researchers have modeled wind power as negative load [9]. This model assumes that all wind energy generated is consumed by the load, and therefore, is not suitable for high wind penetration scenarios where wind energy curtailments occasionally occur. The proposed method models the wind energy curtailment in the first step, and then applies the negative load approach by chronologically subtracting the actual wind power consumed by the load.
With the growth in wind penetration, the wind farms are distributed at different geographical locations with different wind profiles that are correlated to a certain degree. References [10,11,12] present techniques to conduct adequacy assessment in composite power systems with multiple wind farms considering wind speed correlation. The results show that wind diversity leads to noticeable improvement in system reliability. Reference [13] shows how wind curtailments due to transmission congestions are expected to increase with wind penetration levels, and discusses the impacts of wind integration on system reliability, stability and system costs. The authors use wind capacity credit to assess the adequacy contribution of wind, which is further discussed with additional reliability metrics in [14]. Most utilities assess wind capacity value based on their contribution to generation reserves [15]. The impact on bulk-system adequacy and the curtailment due to minimum capacity and ramping constraints of committed generation has not been studied. Moreover, the combined effect of wind diversity and wind curtailments due to both transmission and generation constraints on the system reliability has not been considered by previous researchers. Further modifications are made in the proposed technique to include wind diversity in the system adequacy assessment.
This paper is organized as follows. Section 2 introduces the technique to assess the forced wind power curtailment in a power system due to generation ramping constraints. Section 3 presents the proposed bulk system reliability and wind energy benefit assessment technique considering wind energy curtailment. Section 4 illustrates the application of the proposed method in bulk system adequacy assessment of a practical power system. The results of sensitivity studies to assess the impact of wind power growth on bulk system reliability and wind energy utilization are discussed in Section 5. A technique to evaluate the system reliability and wind energy benefits considering the combined effects of forced wind curtailment and wind diversity is described in Section 6. Finally, the conclusions are presented in Section 7.
Wind power generated cannot always be absorbed by power systems with high wind penetrations due to congestion in wind power delivery lines, and limitation in ramp down rates of dispatched generating units for load transfer. An appropriate number of generating units are scheduled during an operating condition to serve the system load, such that the total scheduled capacity exceeds the load by a capacity margin known as the spinning reserve. The operating margin is conventionally determined using the "N-1" criterion [8]. This section describes an analytical technique [16] to quantify the wind power absorption capability of a power system that is constrained by the ramp rates of the generating units serving the system load.
A power system is a continuously operating system, and any given operating state is characterized by the number of generating units in operation or committed (N), the maximum continuous rating (MCR), minimum capacity level (Cmn) and ramp rate (RR) of each generating unit, the power output (Cop) of each unit and wind farm, and the system load (L) at the instant. A generating unit i operating at a capacity Copi will carry a spinning reserve Ri given by (1).
| Ri=MCRi−Copi|Copi>Cmni|N∑i=1Copi=L | (1) |
The maximum ramp down capacity RAMPmax, i of the ith unit is given by (2).
| RAMPmax,i=Copi−Cmni | (2) |
The conventional units must ramp down within an acceptable response time to utilize any wind power that will be available during the operating condition. The ramp down capacity of the ith unit in a response time T can, however be restricted by its ramp rate RRi as shown in (3).
| RAMPi={RRi∗T,RAMPmax,i≥RRi∗T)RAMPmax,i,otherwise | (3) |
The maximum wind power that can be absorbed during the operating state is equal to the total ramp down capability of the scheduled generation within the response time. This is termed as the wind power absorption capability (WPAC), and is expressed in percentage of the load served as shown in (4).
| WPAC=N∑i=1RAMPiL×100 | (4) |
The WPAC of the system will vary depending on the number and types of generating units scheduled to meet the load that varies between a minimum value and the system peak throughout the year. The following steps illustrate the process to determine the WPAC of all possible generation schedules of a power system:
1. Start the process from the minimum system load.
2. Schedule generating units from the priority loading order to meet the load using a unit commitment criterion such as the N-1. A probabilistic unit commitment criterion, such as the unit commitment risk [17] can also be used.
3. Dispatch the committed units to meet the load using an economic load dispatch, or other risk based load dispatch [18] methods.
4. Calculate the WPAC for the operating condition.
5. Add the subsequent generating unit from priority loading order to the generation schedule.
6. Determine the load served by the updated generation schedule using the selected unit commitment criterion.
7. Repeat steps 3 to 6 until the load equals the annual peak.
The WPAC of a system depends on the generation schedule. An expected WPAC (EWPAC) can be calculated for the system using (5) by multiplying the WPACi of a generation schedule by its probability Pi for all n possible generation schedules. In order to improve the evaluation accuracy, a multi-interval EWPAC can similarly be calculated for generation schedules grouped into different interval of load levels, such as high and low load.
| EWPAC=n∑i=1WPACi∗Pi | (5) |
Generating unit data such as the type, MCR, forced outage rate (FOR) [1] and bus location are the required inputs to the probabilistic models for the conventional generating units. Large thermal units or combined cycle gas turbine (CCGT) units generally reside in one or more derated states due to partial outages. Energy limited units, such as hydro units, also reside in multiple output states due to flow restrictions. Such units can be represented by multi-state Markov models [8]. The transmission lines are represented by two-state Markov models [8]. Transmission line data such as the line length, resistance, reactance, power transfer capacity, repair time and failure rates [8] are the required inputs to the probabilistic models for transmission lines. Annual reliability indices are usually computed using a load duration curve (LDC).
Hourly wind speed data is simulated using time series models developed for the particular wind sites, and are sequentially compared with the hourly load to assess the forced wind power curtailed. Reference [19] shows that an ARMA model can be used to represent the long term wind characteristics of a specific wind site. The ARMA model time series yt for the Swift Current wind site in Saskatchewan is shown in (6),
| yt=1.1772yt−1+0.1001yt−2−0.3572yt−3+0.0379yt−4+αt−0.5030αt−1−0.2924αt−2+0.1317αt−3αt∈NID(0,0.5247602) | (6) |
where, αt is a normally and independently distributed white noise with zero mean and variance of 0.5247602 at hour t. A series of yt can be generated from (6) using the values of αt randomly generated for each hour and the preceding values of y and α. The simulated hourly wind speeds can then be computed using (7).
| SWt=μt+σt⋅yt | (7) |
where, SWt is the simulated wind speed for hour t, µt is the hourly mean wind speed for hour t and σt is the hourly standard deviation of wind speed for hour t.
The hourly mean and standard deviation of the wind speed at the Swift Current wind site is obtained from Environment Canada [20]. Hourly wind speed data is simulated for 1000 yearly samples using (7). Subsequently, the hourly wind power output of the wind turbine generator (WTG) is computed using the power curve relation in (8).
| P(v)={0,0≤v<Vci(A+Bv+Cv2)Pr,Vci≤v<VrPr,Vr≤v<Vco0v≥Vco | (8) |
where, Pr is the rated capacity of the WTG, Vci is the cut-in speed, Vr is the rated speed, Vco is the cut-out speed, and the constants A, B and C depend on the values of Vci, Vr and Vco [21]. The Vci, Vr and Vco of 15 km/h, 50 km/h, and 90 km/h respectively were used in the subsequent studies.
The wind power in excess of the WPAC calculated for a load level is spilled during the operating condition, while the remainder of the wind power available at the time is utilized to serve the load. The hourly values of the wind power absorbed (WPA) from the wind farm are found using (9).
| WPA(t,int)={EWPACint∗L(t,int),WP(t)>EWPACint∗L(t,int)WP(t),otherwise. | (9) |
where, WP(t) is the wind farm power output at hour t, and L(t, int) is the load at hour t and lies in the interval, int.
A wind capacity model is created by building a discrete probability distribution of the hourly WPA values. The number of class intervals and the width of each interval in the discrete probability distribution is found using Sturges' rule [22]. The MECORE software allows a maximum of 10 wind power output states. An apportioning method is used to reduce the number of output states in the probability distribution table from 22 to 10, and create a 10-state wind power model.
The wind power is modeled as negative load in studies that do not consider transmission constraints. The chronological annual load is modified by subtracting the WPA in the corresponding hours, and averaged over s simulation years as shown in (10). The averaging is done to recognize the diurnal and seasonal variation in wind power from year to year. The modified hourly loads are sorted in a descending order to obtain the load duration curve.
| {ML(t)}t=1to8760={(1/s)SUMj=1tos(L(t)−WPA(t)j)}t=1to8760 | (10) |
This section presents the proposed method for bulk system adequacy evaluation considering forced wind power curtailment. A reliability software called MECORE [23] is used which utilizes a single load model to represent the load profile at all the load buses in the system to evaluate the annual adequacy indices. When wind power curtailment is considered in the adequacy analysis, the load profile for the buses connected to wind farms will be different from that of the other buses. MECORE can also be used to obtain annualized reliability indices by considering different load values at different buses. In this option, however, the load at each bus can only be represented by a single peak load value.
In the proposed method, the modified LDC at each of the system buses are discretized into NS number of states, and a discrete probability distribution is obtained for each load bus. The MECORE software is run NS times using different single load values for the different load buses and the annual HL II reliability indices are computed by weighting the annualized indices at every load level by the load level probability. This method can incorporate different load models to represent the loads profiles at different load buses. The annual risk index or wind energy utilization index for a particular load point collectively denoted as RLP is evaluated using (11).
| RLP=NS∑i=1Ri,LP∗pi | (11) |
where, Ri, LP denotes the reliability or energy index obtained using the single value load for load step i, and pi denotes the probability of load step i. RLP represents a basic risk index or a wind energy utilization index obtained by performing the iterative annualized analysis. The actual value of the load at each load step is calculated from the per unit value using (12) and (13) for buses with and without wind resources.
| LSi,LP∈NW=LSi,p.u.,LP×PLLP | (12) |
| LSi,LP∈W=LSi,p.u.,LP×MPLLP | (13) |
where, LSi, p.u., LP is the per unit value of the load step i, PLLP is the peak load and MPLLP is the modified peak load at the Load Point LP, and the sets W and NW respectively include all load points with and without wind power connection.
The reliability index and the wind energy utilization index for the entire bulk power system can be found by aggregating the individual load point indices using (14).
| Rsystem,annual=NL∑LP=1RLP | (14) |
where, NL represents the number of load points in the power system.
It is important to select an appropriate number of load steps or NS in (11) such that the computation is both fast and reasonably accurate. System reliability studies were conducted using the proposed HL II evaluation technique to determine the appropriate number of load steps. Starting with NS = 40, the number of load steps was decreased to 30, 20 and 15. The test system, the IEEE-RTS [24], was used for the studies. A range of studies was carried out with and without considering the transmission system, with and without considering wind integration, and at different peak load levels, in order to assess the appropriate number of load steps in the load model at different system configurations.
It was observed that with the increase in the number of load steps from 15 to 40, the values of the reliability indices decreased as the accuracy increased. However, there was an increase in the computation time as NS is increased from 15 to 40. Considering the loss of load expectation (LOLE) [8] index using the 40-step load model as the reference, the error in the LOLE values using the 30-step, 20-step and 15-step load models were 0.4%, 12.3% and 29.9% respectively. From these observations, it was concluded that a 30-step load model provides reasonable accuracy in the results with reduced computation time.
Figure 1 shows the 30-step annual LDC of the IEEE-RTS without wind power. In subsequent sections, load models were also developed considering wind curtailment with different installed wind capacities at a wind farm location.
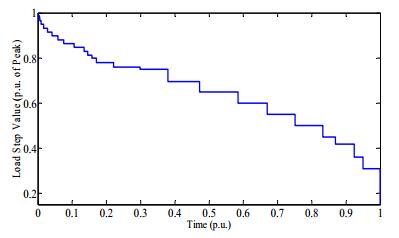 Figure 1. Annual 30-step load model of the IEEE-RTS.
Figure 1. Annual 30-step load model of the IEEE-RTS.Important indices are proposed and introduced in this section to quantify the energy and environmental benefits from wind energy utilization. The expected wind energy supplied (EWES) is obtained using (15) by aggregating the wind energy absorbed by a system at each load step in (11).
| EWES=n∑p=1(ENSp,no wind−ENSp) | (15) |
where, n is the number of periods in the year, ENSp is the total energy not supplied in period p, and ENSp, no wind is the energy not supplied when wind is excluded.
The annual expected wind energy spilled (WESP) can be calculated using (16).
| WESP=n∑p=1((CSp∑i=1(Ci×Pi))×Tp−ENSp,nowind+ENSp) | (16) |
where, CSp is the number of the discrete capacity states in the wind generation model in the period p, and Ci and Pi are the capacity and probability of the ith state, respectively.
The proposed technique for EWPAC assessment in a wind-integrated system is illustrated on the modified IEEE-RTS. Table I shows the type, location, FOR and MCR data of the generating units added to the IEEE-RTS, designated at the MRTS. The additional generating units are connected to the buses known to have relatively poor reliability. The total conventional generation capacity of the test system is 3859 MW. Ramp down rates of 35, 10 and 2 percent of ratings per minute are considered for hydro, gas and coal units respectively. The annual peak load and minimum load of the system are 3500 MW and 1787 MW respectively.
The evaluation process starts from the base load generation schedule to meet the minimum system load of 1787 MW. An operating reserve is considered to account for the loss of the largest unit. Response times between 5 to 15 minutes have been considered in [6,7] to follow wind variability with conventional unit ramping. The WPAC results for 15 minute response time are shown in Table I for the entire range of generation schedules between the annual minimum load to the system peak load. Each row of Table 1 shows the WPAC for each operating state sequentially obtained by adding one generating unit at a time, according to the priority loading order. The loads served by the each generation schedule to meet the specified operating reserve criterion are also shown.
| Unit type | Unit name | Bus number | FOR (%) | MCR (MW) |
| Hydro | H1 | 6 | 0.58 | 62 |
| H2 | 6 | 6.91 | 62 | |
| H3 | 6 | 0.29 | 62 | |
| H4 | 2 | 0.55 | 34 | |
| H5 | 2 | 1.61 | 34 | |
| H6 | 2 | 0.64 | 34 | |
| H7 | 2 | 1.14 | 34 | |
| H8 | 2 | 1.04 | 34 | |
| H9 | 2 | 1.72 | 34 | |
| H10 | 10 | 1.47 | 42 | |
| H11 | 10 | 0.30 | 42 | |
| H12 | 3 | 0.18 | 14 | |
| H13 | 3 | 0.14 | 14 | |
| H14 | 3 | 2.10 | 14 | |
| H15 | 3 | 1.38 | 14 | |
| H16 | 3 | 0.14 | 15 | |
| H17 | 3 | 0.20 | 15 | |
| H18 | 3 | 0.10 | 15 | |
| H19 | 13 | 0.09 | 85 | |
| H20 | 13 | 0.13 | 85 | |
| CCGT | CT1 | 15 | 4.50 | 260 |
| CT2 | 14 | 3.00 | 228 | |
| CT3 | 9 | 6.00 | 246 | |
| CT4 | 19 | 5.18 | 312 | |
| CT5 | 20 | 6.00 | 246 | |
| SCGT | CT6 | 16 | 2.40 | 56 |
| CT7 | 16 | 2.40 | 56 | |
| CT8 | 16 | 2.40 | 56 |
There are 30 generation schedules for the different load levels in the system shown in Table 2. The 30 schedules are grouped into high and low load intervals in this example. The system load above and below the average annual load was considered as the high load and the low load respectively. The EWAC evaluated using (5) was found to be 23% and 31% respectively for the low and high load period for a response time of 15 minutes. These values are used in a time series simulation to obtain the hourly WPA using the six years of historical wind power data from a 198 MW wind farm with the Swift Current wind data. The WPA values thus obtained were used to create the wind capacity models at the respective buses. The average modified hourly load values can be obtained from (11) for generation adequacy evaluation. The annual LDC thus created considering wind power curtailment is shown in Figure 2. This can be compared with the original annual LDC shown in Figure 1.
| No. of committed units | Total MCR (MW) | Load served (MW) | Load probability | WPAC(%) |
| 26 | 2166 | 1787 | 0.000000 | 20.12 |
| 27 | 2426 | 2047 | 0.000910 | 22.23 |
| 28 | 2654 | 2275 | 0.042223 | 23.05 |
| 29 | 2966 | 2592 | 0.225569 | 24.08 |
| 30 | 3140 | 2766 | 0.211002 | 24.64 |
| 31 | 3254 | 2880 | 0.156985 | 25.86 |
| 32 | 3316 | 2942 | 0.071397 | 27.42 |
| 33 | 3378 | 3004 | 0.055115 | 28.92 |
| 34 | 3463 | 3089 | 0.047964 | 30.87 |
| 35 | 3548 | 3174 | 0.058965 | 32.72 |
| … | … | … | … | … |
| … | … | … | … | … |
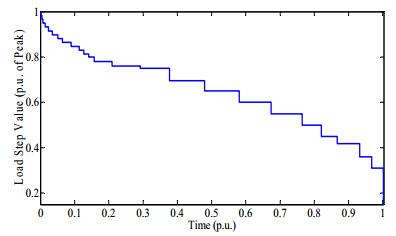 Figure 2. Modified annual 30-step load model incorporating wind curtailment from a 198 MW wind farm.
Figure 2. Modified annual 30-step load model incorporating wind curtailment from a 198 MW wind farm.A bulk system adequacy evaluation of the MRTS was carried out by considering the 198 MW wind farm with Swift Current wind regime connected to Bus 4 of the system. Table 3 shows the LOLE results obtained considering wind power curtailment due to transmission constraint and due to both generation and transmission constraints. The LOLE results are also shown for comparison at higher wind power penetration levels. It is observed from Table 3 that additional wind curtailment due to generation constraints results in an increase in LOLE for the three wind penetration levels. The difference in percent between the system LOLE values with and without considering wind curtailment due to generation constraints is 4.9%, 11.8% and 19.4% when the wind farm capacity is 198 MW, 428 MW and 728 MW, respectively. It is observed that there is a higher percentage difference between the LOLE values as the wind penetration increases. Therefore, it is important to consider wind curtailment due to both generation and transmission constraints to obtain a reasonable assessment of system reliability, especially at high wind penetration levels
| Wind farm capacity (MW) | Wind power penetration (%) | LOLE (h/yr) considering curtailments due to | |
| generation & transmission constraints | transmission constraints | ||
| 198 | 4.9 | 11.12 | 10.58 |
| 428 | 9.9 | 8.42 | 7.41 |
| 728 | 16.0 | 7.59 | 6.12 |
This section examines the impact of wind power growth on wind energy curtailments, and the resulting reliability and energy indices. It is assumed that the wind penetration in the MRTS grows from 4.9%, to 9.9%, and then to 16.0% in the following studies. The resulting installed wind capacities are 198 MW, 428 MW and 728 MW respectively. This study considers both the HL Ⅰ and HL Ⅱ evaluation to compare the impact of forced wind curtailment due to generation and transmission limitations on the system LOLE. Three cases were examined in this study considering: (1) no wind curtailment, (2) wind curtailment due to generation constraints and (3) wind curtailment due to generation and transmission constraints. The LOLE results are shown in Figure 3.
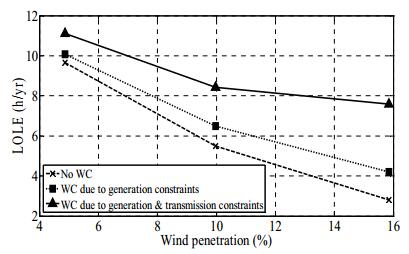 Figure 3. Reliability impact of wind growth with and without considering forced wind curtailment.
Figure 3. Reliability impact of wind growth with and without considering forced wind curtailment.It can be seen that the LOLE decreases with wind power growth for all three cases. It is observed that highly optimistic reliability evaluation results are obtained when forced wind curtailment is not considered. There is an increase in the LOLE as seen in the middle curve in Figure 3 when wind curtailment due to generation constraints is considered. The LOLE are increased by 4.4%, 16.2% and 40.2% respectively at the three wind penetration levels in increasing order. With the consideration of generation and transmission constraints in the adequacy assessment, the LOLE values increase further by 10.4%, 25.2% and 65.3% at the three wind penetration levels in increasing order, as shown by the top curve in Figure 3. The figure shows that the impact on system adequacy of forced wind curtailments increase substantially as the wind penetration grows in a power system.
The system peak load carrying capability (PLCC) was evaluated for the three cases considering a LOLE criterion of 1 hr/yr. Table 4 shows the PLCC for the three cases for the three wind power penetration levels, i.e, 198 MW, 428 MW and 728 MW. The table also shows the increase in PLCC (IPLCC) due to the addition of wind power. The IPLCC is also known as the effective load carrying capacity (ELCC) of the wind farm, and sometimes referred to as the capacity credit of the wind farm when expressed in percentage of the rated wind farm capacity. The last row in Table 4 shows the PLCC and IPLCC for Case (1) which does not consider forced wind curtailment in the evaluation. When wind curtailment from generation constraints is considered in Case (2), the IPLCC decrease by 1.2 MW, 4.2 MW and 8 MW respectively at the three wind penetration levels in the increasing order. Table 4 shows that the IPLCC are further reduced by 4.5 MW, 8.7 MW and 13.3 MW respectively at the three wind penetration levels in Case (3) when forced wind power curtailment from both the generation and transmission constraints are considered. It can be seen that there are larger reductions in wind power capacity credit values due to forced wind power curtailment at higher wind penetrations.
| Wind penetration | PLCC (MW) at | IPLCC (MW) at | |||||
| 4.9% | 9.9% | 16.0% | 4.9% | 9.9% | 16.0% | ||
| Case (3) | 2653.2 | 2665.4 | 2686.4 | 59.4 | 94.5 | 128.2 | |
| Case (2) | 2680.5 | 2702.8 | 2771.9 | 64.0 | 103.2 | 141.5 | |
| Case (1) | 2681.2 | 2705.9 | 2777.9 | 65.2 | 107.4 | 149.7 | |
The wind energy supplied (WES) and the wind energy spilled (WESP) were also evaluated to assess the impact of forced wind power curtailment on wind energy utilization as wind power penetration is increased in a system. The total expected wind energy available at the wind site for the three penetration levels are 500.0, 1167.6 and 2065.2 GWh per year in the increasing order. The WES increases with wind penetration. There is no wind energy spillage in Case (1) as wind energy curtailments are not considered. The WES and WESP in percent of the available wind energy are shown in Figure 4 for Case (2) and Case (3), respectively with increasing wind penetration. Figure 4(a) shows that the wind energy spilled increases by 0.04%, 5.00% and 11.12% of the available wind energy due to forced wind energy curtailment from generation constraints as wind penetration is increased from 198 MW, 428 MW to 728 MW respectively when only generation constraints are considered. Figure 4(b) on the other hand shows that the wind energy spilled increases by 1.88%, 16.33% and 20.32% for Case (3) when forced wind power curtailment from both the generation and transmission constraints are considered. The results obtained are specific to the test system under study. The wind energy spilled can be relatively high in systems that have generating units with slow ramping and/or high minimum capacity limits, and gusty wind profile with wind capacity concentrated at one particular geographic location causing highly correlated variations and location-specific transmission congestions. The offset in conventional fuel due to wind energy utilization results in the reduction in greenhouses gas emissions. However, the utilization of wind energy can be noticeably reduced due to forced curtailment of wind energy.
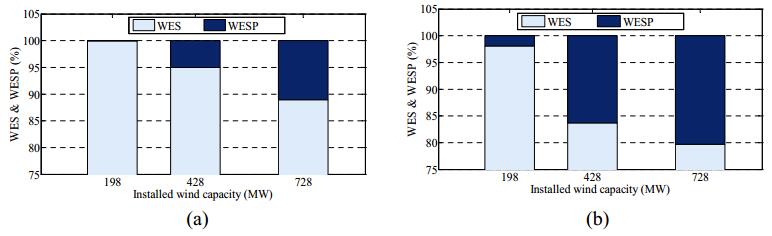 Figure 4. Impact of wind growth on the wind energy utilization considering wind curtailment due to (a) generation constraints (b) generation and transmission constraints.
Figure 4. Impact of wind growth on the wind energy utilization considering wind curtailment due to (a) generation constraints (b) generation and transmission constraints.As wind power penetration continues to increase, many power systems will be connected to multiple wind farms in diverse geographic locations. It has been discussed in Section I that wind diversity significantly effects the bulk power system reliability and wind energy utilization. This section presents a technique to incorporate wind diversity and forced wind power curtailment in bulk system reliability evaluation and wind energy utilization in power systems.
The development of the proposed technique is illustrated by considering a power system connected to two wind farms, WF1 and WF2, located at two different sites. These sites are assumed to have wind characteristics of Swift Current and Regina in the province of Saskatchewan. The wind speed characteristic of WF1 is represented by the ARMA model in (7), and that of WF2 [19] is represented by the time series, yt in (17).
| yt=0.9336yt−1+0.4506yt−2−0.5545yt−3+0.1110yt−4+αt−0.2033αt−1−0.4684αt−2+0.2301αt−3αt∈NID(0,0.4094232) | (17) |
The two sets of hourly wind speed data are simulated with correlated random numbers in order to obtain a particular correlation between the two wind sites. The generation of correlated random numbers can be achieved using different techniques. The proposed technique uses the Cholesky Decomposition [25] method, and (18) is used to generate a set of correlated random numbers.
| XC=X1⋅σ+X2⋅√1−σ2 | (18) |
where, X1 and X2 are a series of uncorrelated random numbers, σ is the desired correlation coefficient for WF2 which can be varied between 0 and 1. Series XC obtained using (18) has a correlation of σ with series X1.
The wind speed series for WF1 can be simulated using the random number series X1 in (6) and (7). The wind speed series for WF2 can be simulated using the random number series XC in (18) and (7). The hourly mean and hourly standard deviation values used for the two wind sites were obtained from Environment Canada [20]. Wind speed data for 1000 yearly samples were simulated for both the wind sites. The hourly wind power outputs for the two sites are then computed using the power curve relation in (8), and sequentially compared with the load to obtain the hourly WPA from (9) using the calculated EWPAC for the different load intervals from (5). Wind capacity models are created for the two sites by developing 10-step discrete probability distributions of the WPA values. The advantage of the technique described in this section is that both the forced wind power curtailment and diversity effects are included in the bulk system reliability evaluation. The 30-step load model shown in Figure 1 represents the load characteristics at the load buses. The load point reliability and wind energy utilization indices are computed using (11). The reliability and the wind energy utilization indices for the entire power system are found using (14).
A study was carried out on the MRTS assuming the wind farms WF1 and WF2 connected at Bus 4 and Bus 19 respectively. Three different correlation coefficients, 0, 0.38 and 0.65 were used in the following studies to investigate the impact of varying the wind diversity between the two wind farms. Three different wind penetrations were considered. The first case considers 171.6 MW Swift Current farm WF1 and 26.4 MW Regina farm WF2, with a total wind capacity of 198 MW. The second case considers adding 230 MW at WF1 increasing the total wind capacity to 428 MW. The third case considers adding 300 MW at WF2 to raise the wind capacity to 728 MW. Forced wind curtailments due to both the generation and transmission constraints were considered. Table 5 shows the system LOLE and the WES obtained considering the three different levels of wind diversity between the two wind farms considering the three wind penetration levels.
| Correlation coefficient σ | LOLE (h/yr) at wind penetration | WES (%) at wind penetration | |||||
| 4.9% | 9.9% | 16.0% | 4.9% | 9.9% | 16.0% | ||
| 0.65 | 11.09 | 7.57 | 5.39 | 99.16 | 88.55 | 85.89 | |
| 0.38 | 10.84 | 6.94 | 4.55 | 99.27 | 91.77 | 88.18 | |
| 0.00 | 10.53 | 6.20 | 3.61 | 99.42 | 94.67 | 91.06 | |
Table 5 shows that the level of system reliability and WES indices of the MRTS are the highest when there is no correlation between the wind speeds at the two wind farms. The σ between the Swift Current and Regina wind speed data is 0.38. Considering this wind diversity, the system LOLE increases to 2.9%, 10.9% and 26.0%, at the three wind penetration levels in the increasing order. If σ assumed to be 0.65, the system LOLE further increases to 5.3%, 22.1% and 49.3%. It is observed that the percentage difference between the LOLE and WES values obtained when the wind farms are independent and when the wind farms are correlated increases with the increase in wind penetration.
Table 6 compares the wind capacity credit for the above three wind penetration levels with and without considering diversity and forced wind power curtailment. The results in the first row do not incorporate wind curtailment or diversity in the evaluation, and shows that the wind CC decreases with increase in wind penetration in a power system. The results in the second row show decrease in CC when forced wind power curtailment due to both generation and transmission constraints is considered. The last row incorporates both forced wind curtailment and diversity in the evaluation. A comparison of the results in the second and the last row shows that the wind CC increases due to wind diversity.
| Case studies | CC (%) of wind farm at penetration of | ||
| 4.9% | 9.9% | 16.0% | |
| No wind curtailment, no wind diversity | 32.8 | 25.1 | 20.5 |
| Forced wind curtailment, no wind diversity | 30.0 | 22.1 | 17.6 |
| Forced wind curtailment, and wind diversity | 32.0 | 24.1 | 19.2 |
This paper proposes a probabilistic technique to evaluate forced wind power curtailment due to both the generation ramping limitations and the transmission transfer capability constraints, and to integrate the developed technique in composite generation and transmission system reliability evaluation. The presented technique utilizes a probabilistic index to quantify the wind power absorption constraints based on generating unit ramping capabilities and delivery limitations based on transmission line capabilities. The proposed method is then extended to include wind farm diversity in bulk system adequacy evaluation and in assessing the wind energy utilization. The results of studies carried out on a test system show that forced curtailment of wind power has noticeable impact on bulk system adequacy and environmental benefits at moderate penetration levels, and is therefore important to incorporate wind curtailment due to both the generation and transmission constraints to obtain a reasonable assessment of system reliability as wind penetration increases in power systems. There are larger reductions in wind power capacity credit values due to forced wind power curtailment at higher wind penetrations. As wind power penetration continues to increase, many power systems will be connected to multiple wind farms in diverse geographic locations. The proposed bulk system adequacy method that incorporates wind power diversity and forced curtailment can be useful in considering these important factors in assessing the reliability and environmental benefits contributed by wind power in large wind-integrated power systems.
All authors declare there is no conflict in this paper.
| [1] |
Burke DJ, O'Malley MJ (2011) Factors Influencing Wind Energy Curtailment. IEEE T Sust Energy 2: 185–193. doi: 10.1109/TSTE.2011.2104981

|
| [2] | Martín-Martínez S, Gómez-Lázaro E, Molina-Garcia A, et al. (2014) Impact of Wind Power Curtailments on the Spanish Power System Operation. In Proc. 2014 IEEE PES General Meeting Conference & Exposition, pp. 1–5. |
| [3] |
McKenna E, Grünewald P, Thomson M (2015) Going with the wind: temporal characteristics of potential wind curtailment in Ireland in 2020 and opportunities for demand response. IET Renew Power Gen 9: 66–77. doi: 10.1049/iet-rpg.2013.0320

|
| [4] | Karki R, Dhungana D, Shimu S, et al. (2013) Reliability evaluation incorporating the load following capability of wind generation. In Proc. 2013 26th Annual IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), pp. 1–4. |
| [5] |
Gu Y, Xie L (2014) Fast Sensitivity Analysis Approach to Assessing Congestion Induced Wind Curtailment. IEEE T Power Syst 29: 101–110. doi: 10.1109/TPWRS.2013.2282286

|
| [6] | Pierre I (2011) Flexible Generation: Backing Up Renewables. Eurelectric Renewables Action Plan, Eurelectric, Brussels, D/2011/12.105/47. |
| [7] |
Kirby B, Hirst E (1998) Generator Response to Intrahour Load Fluctuations. IEEE T Power Syst 13: 1373–1378. doi: 10.1109/59.736279

|
| [8] | Billinton R, Allan RN (1996) Reliability Evaluation of Power Systems. 2nd ed. New York: Plenum. |
| [9] |
Singh C, Lago-Gonzalez A (1985) Reliability modeling of generations systems including unconventional energy sources. IEEE T Power Appar Syst PAS-104: 1049–1055. doi: 10.1109/TPAS.1985.323455

|
| [10] |
Billinton R, Karki R, Gao Y, et al. (2012) Adequacy Assessment Considerations in Wind Integrated Power Systems. IEEE T Power Syst 27: 2297–2305. doi: 10.1109/TPWRS.2012.2205022

|
| [11] |
Billinton R, Wangdee W (2007) Reliability-Based Transmission Reinforcement Planning Associated With Large-Scale Wind Farms. IEEE T Power Syst 22: 34–41. doi: 10.1109/TPWRS.2006.889126

|
| [12] |
Billinton R, Gao Y, Karki R (2009) Composite System Adequacy Assessment Incorporating Large-Scale Wind Energy Conversion Systems Considering Wind Speed Correlation. IEEE T Power Syst 24: 1375–1382. doi: 10.1109/TPWRS.2009.2023263

|
| [13] | Holttinen H (2017) IEA Wind Task 25 - summary of experiences and studies for wind integration. Proceedings of WIW2017 workshop Vienna, 15–17. |
| [14] | Milligan M, Frew B, Ibanez E, et al. (2016) Capacity value assessments of wind power. |
| [15] | WIREs Energy Environ 6: e226. Available from: https://doi.org/10.1002/wene.226. |
| [16] | Padhee M, Karki R (2016) Reliability/Environmental Impacts of Wind Energy Curtailment due to Ramping Constraints. Int J Syst Assur Eng Manag , Springer. |
| [17] | Aminifar F, Fotuhi-Firuzabad M, Shahidehpour M (2009) Unit Commitment With Probabilistic Spinning Reserve and Interruptible Load Considerations. IEEE T Power Syst 24: 388–397. |
| [18] |
Arriagada E, Lópezet E, López M, et al, (2015) A probabilistic economic dispatch model and methodology considering renewable energy, demand and generator uncertainties. Electr Pow Syst Res 121: 325–332. doi: 10.1016/j.epsr.2014.11.018

|
| [19] |
Billinton R, Chen H, Ghajar R (1996) Time-series models for reliability evaluation of power systems including wind energy. Microelectron Reliab 36: 1253–1261. doi: 10.1016/0026-2714(95)00154-9

|
| [20] | Environment Canada, Canadian Weather Energy and Engineering Datasets (CWEEDS). Available from: ftp://ftp.tor.ec.gc.ca/Pub/ Engineering_Climate_Dataset/Canadian_Weather_ Energy_Engineering_Dataset_CWEEDS_2005/ZIPPED FILES/ENGLISH/. |
| [21] |
Billinton R, Karki R, Gao Y, et al. (2012) Adequacy Assessment Considerations in Wind Integrated Power Systems. IEEE T Power Syst 27: 2297–2305. doi: 10.1109/TPWRS.2012.2205022

|
| [22] |
Sturges HA (1926) The choice of a class interval. J Am Stat Assoc 21: 65–66. doi: 10.1080/01621459.1926.10502161

|
| [23] | Li W (1998) Installation Guide and User's Manual for the MECORE Program. |
| [24] | Subcommittee APM (1979) IEEE Reliability Test System. IEEE T Power Appar Syst 98: 2047–2054. |
| [25] |
Dhungana D, Karki R (2015) Data Constrained Adequacy Assessment for Wind Resource Planning. IEEE T Sust Energ 6: 219–227. doi: 10.1109/TSTE.2014.2364778

|
| 1. | Tarek Ibrahim, Farouk Hachem, Mohamad Ramadan, Jalal Faraj, Georges El Achkar, Mahmoud Khaled, Cooling PV panels by free and forced convections: Experiments and comparative study, 2023, 11, 2333-8334, 774, 10.3934/energy.2023038 |
| Unit type | Unit name | Bus number | FOR (%) | MCR (MW) |
| Hydro | H1 | 6 | 0.58 | 62 |
| H2 | 6 | 6.91 | 62 | |
| H3 | 6 | 0.29 | 62 | |
| H4 | 2 | 0.55 | 34 | |
| H5 | 2 | 1.61 | 34 | |
| H6 | 2 | 0.64 | 34 | |
| H7 | 2 | 1.14 | 34 | |
| H8 | 2 | 1.04 | 34 | |
| H9 | 2 | 1.72 | 34 | |
| H10 | 10 | 1.47 | 42 | |
| H11 | 10 | 0.30 | 42 | |
| H12 | 3 | 0.18 | 14 | |
| H13 | 3 | 0.14 | 14 | |
| H14 | 3 | 2.10 | 14 | |
| H15 | 3 | 1.38 | 14 | |
| H16 | 3 | 0.14 | 15 | |
| H17 | 3 | 0.20 | 15 | |
| H18 | 3 | 0.10 | 15 | |
| H19 | 13 | 0.09 | 85 | |
| H20 | 13 | 0.13 | 85 | |
| CCGT | CT1 | 15 | 4.50 | 260 |
| CT2 | 14 | 3.00 | 228 | |
| CT3 | 9 | 6.00 | 246 | |
| CT4 | 19 | 5.18 | 312 | |
| CT5 | 20 | 6.00 | 246 | |
| SCGT | CT6 | 16 | 2.40 | 56 |
| CT7 | 16 | 2.40 | 56 | |
| CT8 | 16 | 2.40 | 56 |
| No. of committed units | Total MCR (MW) | Load served (MW) | Load probability | WPAC(%) |
| 26 | 2166 | 1787 | 0.000000 | 20.12 |
| 27 | 2426 | 2047 | 0.000910 | 22.23 |
| 28 | 2654 | 2275 | 0.042223 | 23.05 |
| 29 | 2966 | 2592 | 0.225569 | 24.08 |
| 30 | 3140 | 2766 | 0.211002 | 24.64 |
| 31 | 3254 | 2880 | 0.156985 | 25.86 |
| 32 | 3316 | 2942 | 0.071397 | 27.42 |
| 33 | 3378 | 3004 | 0.055115 | 28.92 |
| 34 | 3463 | 3089 | 0.047964 | 30.87 |
| 35 | 3548 | 3174 | 0.058965 | 32.72 |
| … | … | … | … | … |
| … | … | … | … | … |
| Wind farm capacity (MW) | Wind power penetration (%) | LOLE (h/yr) considering curtailments due to | |
| generation & transmission constraints | transmission constraints | ||
| 198 | 4.9 | 11.12 | 10.58 |
| 428 | 9.9 | 8.42 | 7.41 |
| 728 | 16.0 | 7.59 | 6.12 |
| Wind penetration | PLCC (MW) at | IPLCC (MW) at | |||||
| 4.9% | 9.9% | 16.0% | 4.9% | 9.9% | 16.0% | ||
| Case (3) | 2653.2 | 2665.4 | 2686.4 | 59.4 | 94.5 | 128.2 | |
| Case (2) | 2680.5 | 2702.8 | 2771.9 | 64.0 | 103.2 | 141.5 | |
| Case (1) | 2681.2 | 2705.9 | 2777.9 | 65.2 | 107.4 | 149.7 | |
| Correlation coefficient σ | LOLE (h/yr) at wind penetration | WES (%) at wind penetration | |||||
| 4.9% | 9.9% | 16.0% | 4.9% | 9.9% | 16.0% | ||
| 0.65 | 11.09 | 7.57 | 5.39 | 99.16 | 88.55 | 85.89 | |
| 0.38 | 10.84 | 6.94 | 4.55 | 99.27 | 91.77 | 88.18 | |
| 0.00 | 10.53 | 6.20 | 3.61 | 99.42 | 94.67 | 91.06 | |
| Case studies | CC (%) of wind farm at penetration of | ||
| 4.9% | 9.9% | 16.0% | |
| No wind curtailment, no wind diversity | 32.8 | 25.1 | 20.5 |
| Forced wind curtailment, no wind diversity | 30.0 | 22.1 | 17.6 |
| Forced wind curtailment, and wind diversity | 32.0 | 24.1 | 19.2 |
| Unit type | Unit name | Bus number | FOR (%) | MCR (MW) |
| Hydro | H1 | 6 | 0.58 | 62 |
| H2 | 6 | 6.91 | 62 | |
| H3 | 6 | 0.29 | 62 | |
| H4 | 2 | 0.55 | 34 | |
| H5 | 2 | 1.61 | 34 | |
| H6 | 2 | 0.64 | 34 | |
| H7 | 2 | 1.14 | 34 | |
| H8 | 2 | 1.04 | 34 | |
| H9 | 2 | 1.72 | 34 | |
| H10 | 10 | 1.47 | 42 | |
| H11 | 10 | 0.30 | 42 | |
| H12 | 3 | 0.18 | 14 | |
| H13 | 3 | 0.14 | 14 | |
| H14 | 3 | 2.10 | 14 | |
| H15 | 3 | 1.38 | 14 | |
| H16 | 3 | 0.14 | 15 | |
| H17 | 3 | 0.20 | 15 | |
| H18 | 3 | 0.10 | 15 | |
| H19 | 13 | 0.09 | 85 | |
| H20 | 13 | 0.13 | 85 | |
| CCGT | CT1 | 15 | 4.50 | 260 |
| CT2 | 14 | 3.00 | 228 | |
| CT3 | 9 | 6.00 | 246 | |
| CT4 | 19 | 5.18 | 312 | |
| CT5 | 20 | 6.00 | 246 | |
| SCGT | CT6 | 16 | 2.40 | 56 |
| CT7 | 16 | 2.40 | 56 | |
| CT8 | 16 | 2.40 | 56 |
| No. of committed units | Total MCR (MW) | Load served (MW) | Load probability | WPAC(%) |
| 26 | 2166 | 1787 | 0.000000 | 20.12 |
| 27 | 2426 | 2047 | 0.000910 | 22.23 |
| 28 | 2654 | 2275 | 0.042223 | 23.05 |
| 29 | 2966 | 2592 | 0.225569 | 24.08 |
| 30 | 3140 | 2766 | 0.211002 | 24.64 |
| 31 | 3254 | 2880 | 0.156985 | 25.86 |
| 32 | 3316 | 2942 | 0.071397 | 27.42 |
| 33 | 3378 | 3004 | 0.055115 | 28.92 |
| 34 | 3463 | 3089 | 0.047964 | 30.87 |
| 35 | 3548 | 3174 | 0.058965 | 32.72 |
| … | … | … | … | … |
| … | … | … | … | … |
| Wind farm capacity (MW) | Wind power penetration (%) | LOLE (h/yr) considering curtailments due to | |
| generation & transmission constraints | transmission constraints | ||
| 198 | 4.9 | 11.12 | 10.58 |
| 428 | 9.9 | 8.42 | 7.41 |
| 728 | 16.0 | 7.59 | 6.12 |
| Wind penetration | PLCC (MW) at | IPLCC (MW) at | |||||
| 4.9% | 9.9% | 16.0% | 4.9% | 9.9% | 16.0% | ||
| Case (3) | 2653.2 | 2665.4 | 2686.4 | 59.4 | 94.5 | 128.2 | |
| Case (2) | 2680.5 | 2702.8 | 2771.9 | 64.0 | 103.2 | 141.5 | |
| Case (1) | 2681.2 | 2705.9 | 2777.9 | 65.2 | 107.4 | 149.7 | |
| Correlation coefficient σ | LOLE (h/yr) at wind penetration | WES (%) at wind penetration | |||||
| 4.9% | 9.9% | 16.0% | 4.9% | 9.9% | 16.0% | ||
| 0.65 | 11.09 | 7.57 | 5.39 | 99.16 | 88.55 | 85.89 | |
| 0.38 | 10.84 | 6.94 | 4.55 | 99.27 | 91.77 | 88.18 | |
| 0.00 | 10.53 | 6.20 | 3.61 | 99.42 | 94.67 | 91.06 | |
| Case studies | CC (%) of wind farm at penetration of | ||
| 4.9% | 9.9% | 16.0% | |
| No wind curtailment, no wind diversity | 32.8 | 25.1 | 20.5 |
| Forced wind curtailment, no wind diversity | 30.0 | 22.1 | 17.6 |
| Forced wind curtailment, and wind diversity | 32.0 | 24.1 | 19.2 |