Citation: Angel G. Gonzalez-Rodriguez, Manuel Burgos Payan, Jesús Riquelme Santos, Javier Serrano Gonzalez. Optimization of regular offshore wind-power plants using a non-discrete evolutionary algorithm[J]. AIMS Energy, 2017, 5(2): 173-192. doi: 10.3934/energy.2017.2.173
| [1] | John Koutroumpas, Konstantinos Koutroumpas . Optimal wind farm sitting using high-resolution digital elevation models and randomized optimization. AIMS Energy, 2015, 3(4): 505-524. doi: 10.3934/energy.2015.4.505 |
| [2] | Takvor Soukissian, Anastasios Papadopoulos, Panagiotis Skrimizeas, Flora Karathanasi, Panagiotis Axaopoulos, Evripides Avgoustoglou, Hara Kyriakidou, Christos Tsalis, Antigoni Voudouri, Flora Gofa, Petros Katsafados . Assessment of offshore wind power potential in the Aegean and Ionian Seas based on high-resolution hindcast model results. AIMS Energy, 2017, 5(2): 268-289. doi: 10.3934/energy.2017.2.268 |
| [3] | Yanting Liu, Zhe Xu, Yongjia Yu, Xingzhi Chang . A novel binary genetic differential evolution optimization algorithm for wind layout problems. AIMS Energy, 2024, 12(1): 321-349. doi: 10.3934/energy.2024016 |
| [4] | Navid Majdi Nasab, Jeff Kilby, Leila Bakhtiaryfard . Integration of wind and tidal turbines using spar buoy floating foundations. AIMS Energy, 2022, 10(6): 1165-1189. doi: 10.3934/energy.2022055 |
| [5] | Ferhat Bingol . Feasibility of large scale wind turbines for offshore gas platform installation. AIMS Energy, 2018, 6(6): 967-978. doi: 10.3934/energy.2018.6.967 |
| [6] | YingTung Chen, Kristina Knüpfer, Miguel Esteban, Tomoya Shibayama . Analysis of the impact of offshore wind power on the Japanese energy grid. AIMS Energy, 2023, 11(1): 110-134. doi: 10.3934/energy.2023006 |
| [7] | Sunimerjit Kaur, Yadwinder Singh Brar, Jaspreet Singh Dhillon . Multi-objective real-time integrated solar-wind-thermal power dispatch by using meta-heuristic technique. AIMS Energy, 2022, 10(4): 943-971. doi: 10.3934/energy.2022043 |
| [8] | Wen-Tien Tsai . Overview of wind power development over the two past decades (2000-2019) and its role in the Taiwan's energy transition and sustainable development goals. AIMS Energy, 2021, 9(2): 342-354. doi: 10.3934/energy.2021018 |
| [9] | Ladislas Mutunda Kangaji, Atanda Raji, Efe Orumwense . Cutting-edge progress in offshore wind and tidal stream power technology—State-of-the-Art. AIMS Energy, 2025, 13(1): 188-230. doi: 10.3934/energy.2025007 |
| [10] | Mohamed Hamdi, Hafez A. El Salmawy, Reda Ragab . Optimum configuration of a dispatchable hybrid renewable energy plant using artificial neural networks: Case study of Ras Ghareb, Egypt. AIMS Energy, 2023, 11(1): 171-196. doi: 10.3934/energy.2023010 |
One of the keys to success in the development of (onshore) wind energy technology was the chance to test small parks, or even isolated wind turbines. Naturally, it is true that economies of scale apply to onshore wind parks to the extent that, in regions where large suitable and available surfaces exist, only big parks have been installed. However, in marine sites, the wide availability of surface area and the high fixed costs involved, lead to intensive resource exploitation, resulting in the installation of a large concentration of wind turbines. This enforces the application of economies of scale in order to capitalize on this type of facilities, in which the companies involved usually protect their knowledge in the form of confidential data. The sluggish development of offshore wind power plants is partly due to the fact that they are still largely seen as a risky investment and are therefore employed only in countries where most of the available onshore wind resources are already being used.
In order to reduce the risk, once the area that houses the wind farm has been selected, and before undertaking a thorough study of investment feasibility, a search tool is necessary to optimize the profitability of the park over its lifespan, which is a compromise between minimizing the initial investment and maximizing the annual revenue from energy sales. These values, initial investment and annual revenue are determined by the configuration of the park: a suitable choice of this configuration directly affects the viability of the investment.
Due to the large number of variables involved in the design of an offshore wind farm, and the nonlinear influence they exert on the profitability of the park, it remains impossible to use a method of systematic search for the optimal solution. Therefore, and similar to the case of onshore wind power plants, the optimization methods does not accomplish an exhaustive search, and they fail to guarantee the optimal solution being attained. However, the problem definition, and therefore how to deal with the solution, presents significant differences with the onshore case. These distinctive differences have not been fully taken into account so far by commercial optimization applications like Resoft WindFarm or DNV GL's WindFarmer, and moreover they offer a robust but closed software where researchers cannot include their own variations.
Indeed, in the case of onshore locations, where it is possible to install smaller parks, the preferred strategy uses genetic algorithms [1] with a previous discretization of the available area. These algorithms employ a codification (genotypes) of the possible solutions, as in [2,3]. Since the grid dimension is defined and fixed prior to execution of the algorithm, the constraint of the position of the turbines to the centre of their cells impedes the assessment of the possibility of variation of these distances. When the number of turbines of the wind power plant increases, the number of possible solutions increases drastically, and hence, unless guarantees to successfully finding the optimum are relaxed, the time needed to reach the optimum increases by the same ratio.
As an alternative, in this paper we have chosen to address the previously unavoidable limitation of the field of solutions by proposing that the turbines follow a regular pattern [4]. This is coherent with the fact that, to date, most offshore wind farms are set in regular pattern layouts in order to reduce their visual impact and to ensure navigation in the area. Initially, only the rhomboid-shaped pattern is assessed, defined by a set of eight parameters whose values establish the solution to the problem.
This change in the structure of the solution has allowed using a non-discrete evolutionary algorithm. It uses continuous values for the solutions of the problem, instead of coded/discrete solutions used in genetic and discrete evolutionary algorithms, as in [5,6]. In a more advanced work, Réthoré et al [7] presents an optimization framework that can use sequential linear programming or simple genetic algorithms, but still limits the possible layout candidates to a list of fixed points inside the domain boundaries. In this work a gradient-based search is used to speed up the algorithm.
The definition of a search engine based on continuous evolutionary algorithms is a simple task, although it has not been used in wind farm layout optimization problems [1]. As a consequence, there is a set of operations necessary for the evaluation of the objective function that have not been analysed or collected in studies of wind farms: including areas with different bearing capacity, depth contours with varying foundation costs depending on the depth, and the point of transition to the coast. There is another process improvement operation, such as a local search operator based on the gradient, whose particular problematic is also presented.
The remaining sections of the paper are structured as follows. Section 2 lists the set of costs and prices used for the simulations and the sources that include them. They have been necessary for an initial approach to the required investment and its expected profitability. Section 3 explains the proposed algorithm and the necessary functions for the evaluation of the components that affect the investment profitability, which are specific for the offshore installation. It also summarizes the operators used in the proposed evolutionary algorithm, and the gradient based local search method. In Section 4, the simulation results are presented. Section 5 summarizes the presented work and outlines a set of conclusions.
At the end of the paper, an appendix is included dealing with the interpretation of level curves.
The following data have been used for the simulations, obtained from [8]. In order to establish a normalized value (€ at 2016) for each of the items, the costs were converted from the original currency to € at the rate registered in the commissioning year, and then increased according to the accumulated inflation.Such data are realistic but they cannot be considered reliable for a complete and thorough study of the cost of investment and decommissioning. However, since those costs where there is a greater unavailability are fixed costs, such as in grid connection, management, finance and administration, they are not involved in obtaining the best site.
Design and project management: 95 k€/MW.
Vessel mobilization and demobilization: 880 k€ for the lease of two vessels, located at a distance of 500 km from the holding port.
Turbine cost: 900 k€/MW. It comprises the acquisition cost (AC = 85%), the shipping and assembling (SA = 5%), and the electrical installation (EI = 10%) [9].
Foundation cost: 450 k€/MW referred to 15 m depth, with an increase of 2% per metre depth. Regarding the type of soil, the following types have been considered: zone 1, with no increase in the foundation cost; zone 2, with an increase of 30%; zone 3, with an increase of 60%; and zone 0 or forbidden areas, with a very high cost increase.
Acquisition cost of inner array cables, export cables and onshore HV cables: see subsection 2.1.
Installation cost of inner array cables and export cables: 120 €/m and 170 €/m respectively.
Excavation and installation of onshore HV cable: 400 €/m.
Offshore substation: 95 k€/MW.
Power factor compensating devices and shoreline transitions: 128 €/MVA.
Onshore substation: 60 k€/MW.
Connection to the grid: 200 k€/MW.
Operation and maintenance costs: 15 €/MWh with an annual increase of 5%.
SCADA system: 50 k€/turbine.
Decommissioning costs and residual price: 120 k€/MW.
Price of MWh and expected increase: 90€/MWh with an annual increment of ΔpMWh=4.
Table 1 has been obtained from information provided by [10] with respect to two manufacturers, designated as A and B. Original prices were given in $2007/m, and are normalized to €2006/m. These data have been used for the selection of the most suitable cable in terms of the purchase cost and the energy losses over the lifespan of the installation.
| Cross Area | Fixed losses | Variable losses | Imax | Norm. Price |
| (mm2) | (W/m) | (mW/m/A1/2) | (A) | (€2016 /m) |
| A95 | 0 | 0.714 | 380 | 128 |
| A150 | 6 | 0.435 | 430 | 192 |
| A400 | 24 | 0.192 | 680 | 321 |
| A630 | 34 | 0.123 | 780 | 481 |
| A800 | 50 | 0.086 | 900 | 506 |
| B95 | 0 | 0.833 | 260 | 384 |
| B150 | 6 | 0.500 | 360 | 417 |
| B400 | 8 | 0.172 | 640 | 514 |
| B630 | 10 | 0.111 | 790 | 535 |
| B800 | 12 | 0.086 | 900 | 616 |
A supplementary cable extension of 40 m has been added to each turbine for connections.
Table 2, lists the information for 3-core 220 kV subsea cables, and for 1-core copper cables. With regard to the subsea cable, obtained from [11], a J-tube de-rating factor of 0.88 has been applied. The data for the onshore cable (XLPE insulated, corrugated aluminium armoured cable), has been obtained from a manufacturer.
| Export cable | Onshore cable | ||||
| Voltage | Section | Capacity | Norm. Cost | Capacity | Norm. Cost |
| (kV) | (mm2) | (MVA) | (€2016 /m) | (MVA) | (€2016/m) |
| 220 | 500 | 250 | 844 | 273 | 232.8 |
| 220 | 630 | 273 | 946 | 297 | 266.0 |
| 220 | 800 | 295 | 1061 | 314 | 299.3 |
| 220 | 1000 | 314 | 1214 | 348 | 367.3 |
The ultimate goal of this article is to provide the knowledge necessary to program a complete algorithm to obtain the optimal layout of an offshore wind power plant. As a starting point, we impose a rhomboidal shape for the plant, composed of a series of clusters or arrays, each grouping the same number of turbines (see Figure 1). This configuration allows a drastic reduction in the time spent on calculating the power loss due to the wakes, which constitutes, by far, the most time-demanding task on each iteration.
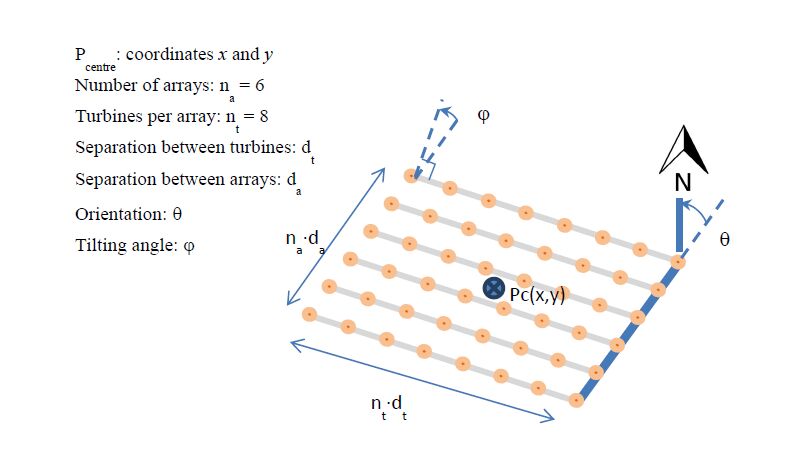 Figure 1. Possible solution for the layout optimization problem following a regular pattern.
Figure 1. Possible solution for the layout optimization problem following a regular pattern.Figure 1 shows a possible solution to the search algorithm. The configuration to be optimized is determined by eight parameters whose values define a possible solution to the problem: number of arrays, na; number of turbines per array, nt; distance between arrays (expressed in turbine diameters), dba; distance between turbines in the same array (in diameters), dbt; orientation with respect to the North θ; the two coordinates of the centre position, Pc(x,y); and tilting angle, ϕ (which is null for the particular case of a rectangle). All the values have a continuous variation range, except for the number of arrays, and the number of turbines per array.
For the sake of operativeness, these last two parameters have been replaced with another two ones: total number of turbines n and quadrature ratio, defined as qt=tan−1(na/nt). This allows certain operators (local search and mutation) to increase the overall number of turbines, n, in one unity in order to explore solutions close to the original one.
To accomplish this objective, a series of partial tasks must be performed. They are presented in the following subsections, although we can anticipate that they can be represented in the flow chart of Figure 2.
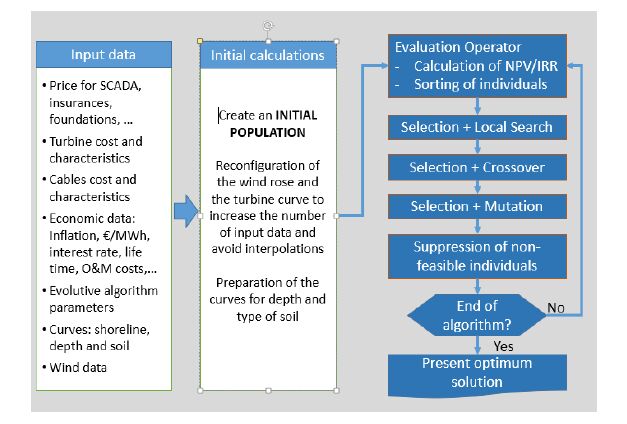 Figure 2. Flow chart for the optimum search algorithm.
Figure 2. Flow chart for the optimum search algorithm.In a first step, the Net Present Value (NPV) was used as Objective Function (OF), as a figure of the investment profitability. NPV is calculated from all economic data relating to the initial cost of investment, operation and maintenance costs, and the income derived from the sale of electricity [3]. It also must include the decommissioning cost, and the residual value of the installation.
However, two main drawbacks have been observed when analysing the simulation results:
•The NPV is a dimensional value and, by itself, does not express a degree of profitability. Another figure, typically the initial investment, must accompany the NPV.
• The solutions tend to include excessive investment since an increase in expenditure is accepted if the NPV is slightly increased after the total lifespan.
For these reasons, the internal rate of return (IRR) is finally selected as the objective function. One of the traditional features of this figure lies in its role of investment quality indicator, in contrast to that of the NPV which strives to increase the shareholders' wealth. However, in the offshore wind farm case, where the economies of scale are strongly present, a high IRR can only be obtained with high investment, which leads to similar solutions to those pursuing an optimum NPV.
The main disadvantage to optimizing the IRR is the fact that the inner-array cables are selected by means of an NPV analysis, and therefore two indicators are used in the overall optimization process.
The search engine is based on a non-discrete evolutionary algorithm whose objective is the maximization of an OF. The algorithm does not use a binary encoding for each parameter but tracks its variability interval in a continuous way. As a consequence, crosses between individuals will be made as weighted averages, and mutations as random assignment. It has also allowed including a local search operator based on the OF gradient.
The evolutionary algorithm starts from an initial population of possible solutions to the problem of wind farm layout optimization. To this end, it assigns random values to each of the parameters involved in the configuration of the wind farm, which are presented in Figure 1. The algorithm then enters an iterative process with the following operators (see Figure 2):
Evaluation operator
This operator calculates the OF for each individual in the generation. The OF is a measure of profitability, in this case the NPV or the IRR. Following, it orders the individuals based on their OF, and selects the best n, where n is the population size (input data).
Selection operator
An individual is pseudo-randomly chosen: in half of the situations, the roulette wheel selection is used, in which those individuals with better OF constitute the fittest individuals with an increased chance of being selected; in the other half, a random individual is chosen. This operator is used for the creation of new individuals via the following three operators.
Local maximum operator
This is shown in subsection 3.4. crossover operator.
Two individuals are selected that behave as parents, and two children are created from them. Their characteristics can be selected, in a random way: either by randomly interchanging the parents' characteristics; or from the average weights of the parents' characteristics.
Mutation operator
A single parent is selected, and a new feasible individual is created in which, for every characteristic, the operator randomly chooses between either copying the parent's characteristic, or randomly deducing a value within the permitted range.
Suppression of non-feasible individuals
There is a high probability that one of the turbines of the newly created individuals lies in a forbidden zone, onshore or outside the search space. Inclusion of the suppression operator as part of the crossing and mutation operators therefore leads to a better result. These operators also suppress an individual if the number of turbines exceeds the permitted one.
The set of points that define the outline of the coast must be given as a part of the input data. Solutions with turbines onshore should be discarded. To this end, appendix 6 indicates an efficient and simple-to-program method to check if a point lies within the closed curve.
The same or a similar procedure is also used for the interpretation of the forbidden zones, areas with different bearing capacity, and depth curves.
The set of forbidden zones is comprised of the prohibited zones due to ecological reasons or maritime transport. Each forbidden zone is a closed curve characterized by a set of points. In the case when the algorithm locates any turbine in a forbidden zone, the individual must be suppressed.
In order to obtain the bearing capacity at a point of the map, it is necessary to perform a set of operations, some of which can be made before launching the iterative search. Other operations will be specific to the position , and therefore they must be performed at every turbine location of each individual (see Figure 3):
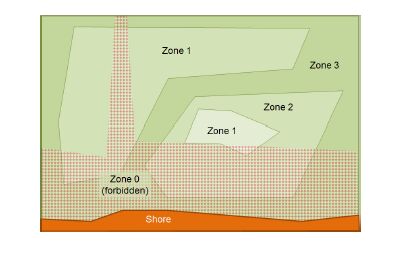 Figure 3. Forbidden zones and curves delimiting the type of sea-bed as a function of its load bearing capacity. Zone 0 = forbidden; zone 1 = reference foundation cost; zone 2, overcost = 30%; zone 3, overcost = 60%.
Figure 3. Forbidden zones and curves delimiting the type of sea-bed as a function of its load bearing capacity. Zone 0 = forbidden; zone 1 = reference foundation cost; zone 2, overcost = 30%; zone 3, overcost = 60%.• As a first step before entering the loop
(a) Read the points of the m curves that define the map of the several types of soil, and their bearing capacities.
(b) Fill in a matrix Ms in which the element ms(i,j) indicates whether the curve i is within the closed curve j.
• Within the iterative process, for each P(x,y)
(a) Obtain the set of curves for which the point P(x,y) lies within.
(b) From among these closed curves, select from matrix Ms the polygon which lies within all the others polygons.
(c) Obtain the bearing capacity of this curve.
The interpretation of depth curves is greatly simplified if these curves are introduced in such a way that, on running their points sequentially, increasing depths are marked on the right (see Figure 4).
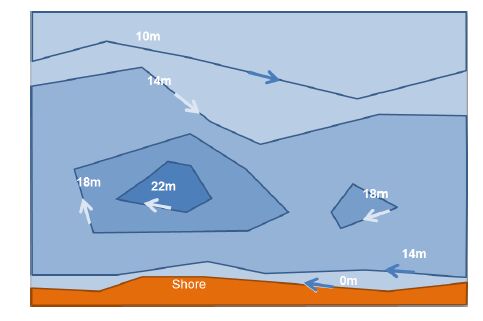 Figure 4. Nautical chart expressing the depth in metres. When travelling along the polygon points, the increasing depths are on the right.
Figure 4. Nautical chart expressing the depth in metres. When travelling along the polygon points, the increasing depths are on the right.In order to obtain the depth at a point P(x,y), it is necessary to carry out the following:
• As a step previous to entering the loop
1. Read every point of the m polygons that define the nautical chart, and their depth.
2. Obtain whether each curve is travelled CW (leaving inside the decreasing values of depth), or CCW (decreasing values). Appendix 6 deals with this problem.
• Within the iterative process, for each P(x,y)
3. Calculate the minimum distance from point P to each curve, and put the curves in order according to their distance.
4. Deduce if the point is at the left or at the right of the closer curve Ccl0 (see Appendix 6).
5. If it is at the right (analogously left), travel the remaining curves in an increasing order of proximity to P, and select the first curve leaving P at its left (right). This curve is designed as Ccl1.
6. Obtain the depth of P as a function of the curve depths Ccl0 and Ccl1, and their distances to P.
A local maximum operator is incorporated, which tracks in the vicinity of a provisional solution in order to obtain the set of values that maximizes the objective function.
Thus, within a generation, the algorithm selects the best individual of each generation, and an additional but randomly chosen individual, and they are both then subject to a local optimization process. This operator is based on the local maximum gradient method for continuous functions. In order to prevent any loss of coherency of the gradient method when applied to dimensional variables, the coordinates must be non-dimensionalized by dividing each coordinate by its corresponding allowable range. This way, if forig(X1,X2,…,Xn) is the original objective function to be optimized, this function must be modified to operate as a function of X=(x1,x2,…,xn)∈Rn, with xj=Xjrange(Xj)
With this change of variables, the optimization process consists of detecting the direction of maximum growth of the resulting objective function f(x1,x2,…,xn), which is parallel to its gradient.
| X=(x1,x2,…,xn)∈Rn,Δmax_growthX||∇f(X) | (1) |
In this case, maximizing the function f(X) starting from an individual with components X=(x1,x2,…,xn) entails:
1. For each component j:
Check if varying the component j by an amount Δtryxj>0 leads to a feasible individual. If so, calculate the relative increase Δf(X)/Δtryxj. If it is not feasible, or there is a decrease in f(X), assign Δf(X)/Δtryxj=0.
Perform the operation above, but this time for Δtryxj<0.
Take ∇jf(X) as the relative increase with the higher absolute value.
2. Deduce the component opt with the higher function increase ∇optf(X)≥∇jf(X)∀j≤n. If it is 0, it is already a local maximum, and the operation ends.
3. Increase every component j by the amount
| Δxj=|Δtryxopt∇optf(X)|∇jf(X) | (2) |
The values of the increments Δtryxj are assigned heuristically. These values should be kept relatively high to speed up the algorithm. Another effect (neither entirely positive nor negative) is the higher probability to escaping from one local maximum to another, and therefore potentially optimum solutions can be inadvertently skipped. This issue cannot be seen as a limitation in the design, since a skipped potentially optimum solution implies that the configuration may be excessively sensitive to the input parameters.
Inclusion of this operator produces an effect similar to particle swarm. It introduces a certain guiding of the individuals in the direction of the gradient of the objective function [12]. The gradient vectors act as the particle swarm velocity vectors, although in the proposed algorithm, the vectors are sporadically applied: when crossing operator creates new individuals with similar characteristics to that of individuals locally optimized (see Figure 5). In this way, part of the local optimization performed over the best individual (parent1 in the figure) is transmitted to its sons.
 Figure 5. Local search optimization producing an effect similar to the guiding vectors of particle swarms. Individuals considering the local optimization are denoted as primed.
Figure 5. Local search optimization producing an effect similar to the guiding vectors of particle swarms. Individuals considering the local optimization are denoted as primed.As previously mentioned, grouping the turbines in a wind park gives rise to a reduction in the produced energy due to the perturbations of upwind turbines in the direction of the flow stream.
In general terms, the net energy generated by the power plant is calculated after evaluating the power deficit that each upwind turbine occasions in each downwind turbine. Furthermore, this calculation must be repeated for all wind speeds considered, and for all wind directions considered. It is possible to implement an improved calculation method to reduce the necessary computation time by a ratio of up to 1/300 with regard to traditional methods.
To this end, a set of operations must be applied:
• Storing the result of certain operations (mainly the position of the individual turbines).
• Disregarding the wake effect between two turbines placed very far apart.
• Disregarding wind directions greatly deviated from the direction that links two turbines.
• Disregarding the wake effect at very high speeds.
• Suppression of unnecessary calculations where no perturbation is expected.
Since the restriction referring to the rhomboidal shape of the wind part is imposed, a set of operations that take advantage of this regular pattern can be done to reduce even more the computational time [13]. These operations lead to an optimized energy calculation method that reduces the computational time by a factor of 1/20000 (for a 100-turbine farm).
In order to obtain the linking point between onshore and offshore, the algorithm uses a simplified method that takes into account neither the orography in the sea, nor the orography on the coast. It only calculates the transition point as a function of shoreline contour, the costs of the high voltage cables, and the costs of its installation.
Figure 6 illustrates the concept that supports the calculation of the position of the shoreline transitions. For each section that makes up the shoreline, we must obtain the point belonging to the line containing the segment, where the overall cost is lower. If the point is beyond the interval of coast evaluated, the closest vertex is chosen.
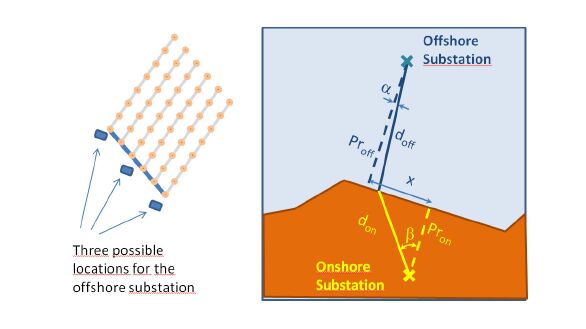 Figure 6. Point of connection between offshore and onshore cables.
Figure 6. Point of connection between offshore and onshore cables.Therefore, the objective consists in minimizing
| doffCoff+donCon=f(don,doff) | (3) |
where off and on stand for offshore and onshore, d is the distance to the transition point and C represents the costs of purchasing and installing the cable. This expression can be rewritten as
| Coff√Proff+(X−tPron)2+ConPron√1+t2 | (4) |
where t=tan(β), and Pr stands for projection (see Figure 6). Minimizing this expression for t is not trivial, and it requires an iterative process to obtain the root of its derivative.
This calculation must be performed for each of the 3 possible locations of the offshore substation with regard to the wind farm (see Figure 6), and the location with the lowest cost (including the substation platform foundation cost) is then selected for the corresponding individual under evaluation.
The current flowing along an array is higher as long as the cable collects the power from more turbines. In this way, several section cables can be used along the same array, thus reducing the expenditure of the electrical infrastructure.
Starting from the information available regarding cable price, capacity and expected losses, an offline analysis has been performed for each stretch along an array. Therefore, by taking the cable cost and its power losses (normalized into present euros) into account, the most suitable cable can be calculated that gives rise to highest NPV over the lifespan. It is worth mentioning that the IRR cannot be used as indicator because investment and flow cash have the same sign.
An application supported by the introduced methodology, has been designed and programmed to search for the optimum layout and relative location of an offshore wind farm that follows a rhomboidal pattern (see Figure 7).
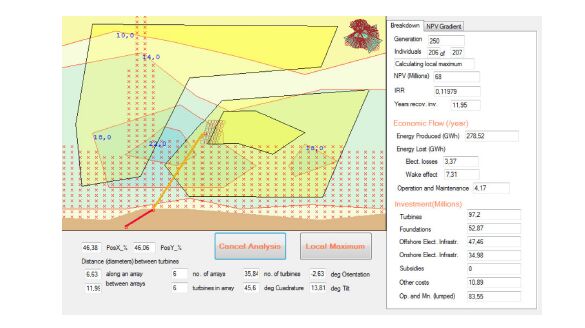 Figure 7. Optimization result. Numerical values for the solution parameters appear in the bottom, and resulting economic data are shown at the right. The wind rose is depicted at the upper-right corner.
Figure 7. Optimization result. Numerical values for the solution parameters appear in the bottom, and resulting economic data are shown at the right. The wind rose is depicted at the upper-right corner.The information relative to the scenario is defined by means of an input file, made up of different sheets related to estimated/measured wind, economic figures, turbine characteristics and costs, foundation types and costs, electrical components, definition of curves for depths, soil and coasts, as well as algorithm parameters.
As can be seen in Figure 7 the following scenario has been selected:
• Studied zone of 80 km × 40 km.
• A wind rose given by:
| Sector | E | SE | S | SW | W | NW | N | NE |
| Probability in % | 15 | 20 | 15 | 15 | 5 | 10 | 10 | 10 |
• Weibull parameters: C param = 8.1 m/s and K param = 2.3.
• The coast is located to the south. The onshore substation is located to the south-west.
• A forbidden strip parallel to the coast, plus an additional perpendicular path for marine sailing is included.
• Three types of soil are considered, the zone 1 being that with highest load-bearing capacity (see Figure 3).
• The sea depth in the administrative concession varies between 10m and 22 m. The curves are represented for 10m, 14 m, 18 m (two curves) and 22 m (see Figure 4 and Figure 7).
• There is a limit of 38 turbines, each of 3 MW. Its power curve is given by:
| ws(m/s) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | ... | 25 |
| (MW) | 0 | 0.09 | 0.22 | 0.43 | 0.71 | 1.11 | 1.55 | 2.02 | 2.39 | 2.77 | 2.91 | 2.95 | 2.98 | 3.00 | ... | 3.00 |
where ws is the wind speed and P is the generated power at this speed.
Evolutive algorithms are efficient in searching the global optimum for complex problems. However, they fail to guarantee the convergence towards the optimum. For this reason, a set of 300 simulations have been performed over the same scenario. In all of them, the obtained solutions fell into the same configuration: 6 arrays of 6 turbines per array (6 × 6). Table 3 summarizes the main results. In half of the simulations (identified by p1), the maximum number of generations was established as 100, and the population size as 80. In the other half (p2) the maximum number of generations was 250, and the population size was 140. The first two columns in this table refer to a set of 100 simulations in which the function objective was the NPV. In the following two columns, simulations refer to an analogous set of simulations in which the function objective was the IRR. The last two rows also refer to simulations with IRR as the objective function, but here the maximum local operator is suppressed.
| p1: max gener = 100 popul. size = 80 p2: max gener = 250 popul. size = 140 |
Objective function = NPV | Objective function = IRR | Objective function = IRR without local search | ||||
| p1 | p2 | p1 | p2 | p1 | p2 | ||
| NPV (M€) | Mean | 67.10 | 67.14 | 67.02 | 67.16 | 66.50 | 66.87 |
| Deviat. | 0.29 | 0.32 | 0.30 | 0.27 | 0.83 | 0.33 | |
| Best | 67.59 | 67.61 | 67.55 | 67.59 | 67.24 | 67.53 | |
| IRR (%) | Mean | 11.936 | 11.935 | 11.937 | 11.943 | 11.916 | 11.931 |
| Deviat. | 0.013 | 0.015 | 0.012 | 0.009 | 0.031 | 0.014 | |
| Best | 11.958 | 11.960 | 11.957 | 11.959 | 11.947 | 11.956 | |
| Time (s) | Mean | 105.1 | 220.6 | 97.9 | 175.7 | 104.1 | 209.3 |
| Deviat | 11.48 | 71.83 | 15.45 | 40.56 | 14.39 | 72.67 | |
| Investment (M€) | Mean | 257.1 | 257.4 | 256.7 | 256.6 | 256.8 | 256.8 |
| Deviat | 0.51 | 0.48 | 0.53 | 0.42 | 0.61 | 0.43 | |
With regard to the rows, this table organizes the obtained information in four blocks. The first block comprises the average NPV, the standard deviation, and the best NPV for every set of 50 executions. The second block is similar, but referred to IRR. The third and fourth blocks show the mean value and standard deviation for, respectively, the computation time and the required investment. As a reference for the computation time, the algorithm was programmed in managed C++, and executed in a notebook Pentium 2.13 GHz. As a comparison, the running time of 50 cases for an OWF with 20 turbines, presented in [14] was 120 h, while with the presented algorithm, the required time for an OWF with 36 turbines is around 100 s (100 generations).
Table 4 gathers the results obtained from the 300 simulations, showing the mean value and standard deviation of the parameters that define the solutions.
| NPV (M) | IRR (%) | ctrx | ctry | ndaa | ndba | θ | Tilt | |
| Mean | 67.0 | 11.933 | 40.9 | 27.5 | 6.7 | 11 | - 22 | 5.4 |
| std | 0.49 | 0.019 | 0.78 | 0.56 | 0.74 | 1.52 | 74.2 | 13.0 |
The following conclusions can be derived from its analysis:
• Regardless of whether the considered OF is NPV or IRR, similar figures are obtained.
• Slightly lower values of investment are required if the OF is the IRR.
• Logically, simulations designed as p2 (higher number of generations and individuals per generation) take considerably more time to reach the optimum. However, the results are not significantly better. Therefore, we recommended performing a higher number of simulations with a lower number of generations and individuals per generation, and then choosing the best solution.
• The local maximum operator increases the mean of the OF for the optimum. It does not entail a significant improvement with regard to the computational time.
In addition to these simulations, further simulations have been performed with higher values for the parameters than those defined for p2. However they have not given rise to a solution with a significantly higher OF with respect to those of Table 3.
Figure 7 shows the solution with the highest IRR among the 100 obtained for the same scenario (OF = IRR, with local maximum operator). As expected, the centre of the solution, and in fact the centres of all the solutions, fall into the zone with the highest load-bearing capacity (zone 1).
As can be extracted from data on the right-hand-side of Figure 7, the cost breakdown obtained is: turbines (39.9%), foundations (21.7%), electrical infrastructure (33.9%), engineering and others (4.5%), which is similar to that obtained from the reviewed papers summarised in Table 5. However, a significant difference exists in the electrical infrastructure that leads to believe that there may be an overestimation of the cable purchase and laying costs. One of the causes of this possible overestimation lies in the fact that the cable for each stretch has been selected such that its NPV is less negative. This leads to the selection of more expensive cables if it guarantees fewer power losses over the total lifespan. Another cause lies in the increase of the copper price.
The aim of this research is to program a non-discrete evolutionary algorithm to optimize the layout of offshore wind farms. In order to delimit the solution space, the layout has been constrained to a rhomboid-shaped regular pattern. So as to accomplish the programming of the optimum search algorithm, two basic keystones must be solved: obtaining realistic data about the costs and characteristics of the most significant items in the wind farms; and providing systematic and simple methods to manage the various depths and types of seabed.
A major additional functionality has also been explained: a gradient-based local maximum operator. Including this operator improves the IRR values for the optimum, although it does not improve the algorithm convergence (in term of computation time) in the studied cases.
Starting from the knowledge of these functionalities, a non-discrete evolutionary algorithm can be easily programmed and tested. The resulting configuration is the logical one, and is located in the zone with the best conditions of depth and type of soil. The final cost per MW and its breakdown are similar to those given in the literature.
Two possible objective functions have been tested: NPV and IRR. The results are very similar, although the option OF = IRR leads to lower investments.
Taking advantage of the rhomboidal shape, the algorithm uses the method presented in [12] to reduce the required time to compute the energy lossed due to the wake effect. As a consequence, the complete algorithm is able to reach an optimum in approximately 100 s (36 turbines, 100 generations, 80 individuals per generation), drastically faster than existing algorithms.
A. Position of a point with regard to a closed curve
It is necessary to program a function to deduce whether a point is inside or outside a closed curve. This function is employed to ascertain: whether a point is on the coast; whether it is in a forbidden zone; to which load-bearing capacity zone it belongs; and in a modified way, to calculate the depth of the sea bed. As an illustration, an example is laid out at the end of the section.
It is convenient to first define the operation ∙+ as well as its opposite ∙− as
| a,b ∈ [−π,π],a∙+b⇔{a+bifa+b∈[−π,π]a+b+2πifa+b<−πa+b−2πifa+b>π | (5) |
| a∙−b⇔{a−bifa−b∈[−π,π]a−b+2πifa−b<−πa−b−2πifa−b>π | (6) |
The operation ∙+ together with the interval [−π,π] constitute an abelian group satisfying commutativity, closure, associativity, existence of neutral element (0), and an opposite element (the opposite of c is −c).
A.1 Point inside a closed curve
With these definitions, and assuming that a closed curve L is composed of a sequence of m points (xi,yi) (in which xm=x0 and ym=y0), then in order to ascertain whether a point is P(xp,yp) inside or outside this curve, it is sufficient to evaluate the summatory
| Γ=m∑k=1{arctan(yk+1−yp,xk+1−xp)∙−arctan(yk−yp,xk−xp)} | (7) |
By means of Stokes' theorem, it can be demonstrated that
| P(x,y)isinsideL⇔Γ=2πor−2π | (8) |
| P(x,y)isoutsideL⇔Γ=0 | (9) |
With this formulation, then Γ=2πor −2π for points belonging to the contour. In order to detect this situation, it is preferable to check each value of the summatory in (7). The point will belong to the contour if and only if any of the addends yields −π or π.
A.2 Curve travelled CW or CCW
The point sequence in a curve indicates if the curve is travelled clockwise (CW), or counter-clockwise (CCW).
As previously seen, if a point P(x,y) is inside the curve, then Γinner=2πor−2π. If the curve is travelled CCW, then Γinner=2π, and the inner points remain on the left of the curve being travelled. Outer points remain on the right.
If the curve is travelled CW, then Γinner=−2π, and the inner points are on the right of the curve being travelled. Outer points remain on the left.
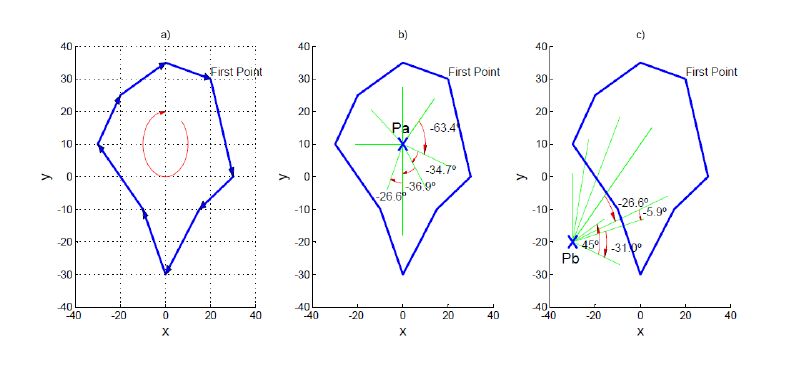 Figure 8. a) Closed curve travelled clockwise; b) differences of angles for an inner point; c) differences of angles for an outer point.
Figure 8. a) Closed curve travelled clockwise; b) differences of angles for an inner point; c) differences of angles for an outer point.However, if no inner points are known, the way to detect whether a curve is travelled CW or CCW is based on the cross product. Thus, a curve is travelled CCW if the summatory of cross products of all of the consecutive segments is negative, and CW if the result is positive.
A.3 Example
We can assume a closed curve defined by
| L≡{(20,30),(30,0),(15,−10),(0,−30),(−10,−10),(−30,10),(−20,25),(0,35),(20,30)}; | (10) |
where, for the sake of space, the z component has been suppressed. By drawing it (see Figure 8a), we could anticipate that it is travelled CW, and we can check it by calculating the summatory of the cross products.
| 8∑i=2(Li+1−Li)×(Li−Li−1)+(L2−L1)×(L1−L8)=550−150+500−200+500++200+300+550=2250>0⇒CW |
If, as an example, we want to test whether point Pa(0,10) is an inner point or outer point, we can calculate every addend in (7). Before checking whether they belong to [−π,π], the list of addends is the following (translated to):
| −63.43 −34.70 −36.87 −26.57 296.57 −36.87 −53.13 −45.00 | (11) |
where the first four values are represented in Figure 8b. After forcing each addend to belong to [−π,π], this becomes
| −63.43 −34.70 −36.87 −26.57 −63.43 −36.87 −53.13 −45.00 | (12) |
Summation of these figures yields −2π. The negative value represents (again) that the curve is travelled CW. The non-null value indicates that point Pa is inside L, and is on the right.
If we want to test the point Pb(−30,−20), then the list of addends is
| −26.57 −5.91 −30.96 45.00 63.43 −12.53 −16.08 −16.39 | (13) |
where all figures belong to [−π,π]. As a sample, the first four values have been represented in Figure 8c. After summing them, this yields 0, and therefore, point Pb is outside L, and is on the left.
All authors declare no conflicts of interest in this paper.
| [1] | Tesauro A, Réthoré P E, and Larsen G C. (2012) State of the art in wind farm optimization. Proc EWEA, 1–11. |
| [2] |
Mosetti G, Poloni C, and Diviacco B. (1994) Optimization of wind turbine positioning in large wind farms by means of a genetic algorithm. J Wind Eng Ind Aerod 51: 105–116. doi: 10.1016/0167-6105(94)90080-9

|
| [3] |
González J, Gonzalez A G, Castro J, et al. (2010) Optimization of wind farm turbines layout using an evolutive algorithm. Renew Energ 35: 1671–1681. doi: 10.1016/j.renene.2010.01.010

|
| [4] | Nielsen P. (2003) Offshore wind energy projects feasibility study guidelines seawind. Tech Rep, Altener Project. |
| [5] |
Hajela P. (1990) Genetic search-An approach to the nonconvex optimization problem. Aiaa J 28: 1205–1210. doi: 10.2514/3.25195

|
| [6] | Serrano J, Burgos M, and Riquelme J M. (2011) An improved evolutive algorithm for large offshore wind farm optimum turbines layout. Power Tech 2011 IEEE Trondheim, 1–6. |
| [7] | Réthoré P E, Fuglsang P, Larsen G C, et al. (2014) Topfarm: multi-fidelity optimization of wind farms. Isope 17: 1797–1816. |
| [8] | Gonzalez A G. (2017) Review of offshore wind farm cost components. Energ Sust Dev, 10–19. |
| [9] | Douglas W. (2010) Offshore wind asessment for Norway. Tech Rep, Norway. |
| [10] | Green J, Bowen A, Fingersh L J, et al. (2007) Electrical collection and transmission systems for offshore wind power. National Renewable Energy Laboratory (U.S.), 1–7. Available from http://www.nrel.gov/docs/fy07osti/41135.pdf. |
| [11] | Offshore development information statement (ODIS). (2009) Appendices. Tech Rep, National Grid. |
| [12] |
Hou P, Hu W, Soltani M, et al. (2015) Optimized placement of wind turbines in large-scale offshore wind farm using particle swarm optimization algorithm. IEEE T Sust Energ 6: 1272–1282. doi: 10.1109/TSTE.2015.2429912

|
| [13] |
Gonzalez A G, Burgos M, Riquelme J, et al. (2015) Reducing computational effort in the calculation of annual energy produced in wind farms. Renew Sust Energ Rev 43: 656–665. doi: 10.1016/j.rser.2014.11.024

|
| [14] |
Pérez B, Mínguez R, and Guanche R. (2013) Offshore wind farm layout optimization using mathematical programming techniques. Renew Energ 53: 389–399. doi: 10.1016/j.renene.2012.12.007

|
| [15] | Offshore Design Engineering (ODE) Limited. (2007) Study of the costs of offshore wind generation. Tech Rep URN number 07/779, Renewables Advisory Board (RAB) & DTI. Available from http://webarchive.nationalarchives.gov.uk/+/http:/www.berr.gov.uk/files/file38125.pdf. |
| [16] | Morgan C A, Snodin H M, and Scott N C. (2003) Offshore wind economies of scale, engineering resource and load factors. Tech Rep, Garrad Hassan. |
| [17] | Slengesol I, De Miranda W P, Birch N et al. (2010) Offshore wind experiences: a bottom-up review of 16 projects. Tec Rep, OceanWind. |
| [18] | Wind Energy-The facts. (2009) Economics: the cost of energy generated by offshore wind power. EWEA. Available from https://www.wind-energy-the-facts.org/images/chapter3.pdf. |
| 1. | Arthur Leandro Guerra Pires, Paulo Rotella Junior, Sandra Naomi Morioka, Luiz Célio Souza Rocha, Ivan Bolis, Main Trends and Criteria Adopted in Economic Feasibility Studies of Offshore Wind Energy: A Systematic Literature Review, 2021, 15, 1996-1073, 12, 10.3390/en15010012 | |
| 2. | Angel Gaspar Gonzalez-Rodriguez, Juan Manuel Roldan-Fernandez, Javier Serrano-Gonzalez, José Vicente Muñoz-Díez, Gradient Descent Algorithm with Greedy Repositioning Using Power Deficit Aggregation of Wakes to Accelerate the Offshore Wind Farm Layout Optimization Problem in Irregular Concession Areas, 2024, 14, 2076-3417, 11331, 10.3390/app142311331 |
| Cross Area | Fixed losses | Variable losses | Imax | Norm. Price |
| (mm2) | (W/m) | (mW/m/A1/2) | (A) | (€2016 /m) |
| A95 | 0 | 0.714 | 380 | 128 |
| A150 | 6 | 0.435 | 430 | 192 |
| A400 | 24 | 0.192 | 680 | 321 |
| A630 | 34 | 0.123 | 780 | 481 |
| A800 | 50 | 0.086 | 900 | 506 |
| B95 | 0 | 0.833 | 260 | 384 |
| B150 | 6 | 0.500 | 360 | 417 |
| B400 | 8 | 0.172 | 640 | 514 |
| B630 | 10 | 0.111 | 790 | 535 |
| B800 | 12 | 0.086 | 900 | 616 |
| Export cable | Onshore cable | ||||
| Voltage | Section | Capacity | Norm. Cost | Capacity | Norm. Cost |
| (kV) | (mm2) | (MVA) | (€2016 /m) | (MVA) | (€2016/m) |
| 220 | 500 | 250 | 844 | 273 | 232.8 |
| 220 | 630 | 273 | 946 | 297 | 266.0 |
| 220 | 800 | 295 | 1061 | 314 | 299.3 |
| 220 | 1000 | 314 | 1214 | 348 | 367.3 |
| p1: max gener = 100 popul. size = 80 p2: max gener = 250 popul. size = 140 |
Objective function = NPV | Objective function = IRR | Objective function = IRR without local search | ||||
| p1 | p2 | p1 | p2 | p1 | p2 | ||
| NPV (M€) | Mean | 67.10 | 67.14 | 67.02 | 67.16 | 66.50 | 66.87 |
| Deviat. | 0.29 | 0.32 | 0.30 | 0.27 | 0.83 | 0.33 | |
| Best | 67.59 | 67.61 | 67.55 | 67.59 | 67.24 | 67.53 | |
| IRR (%) | Mean | 11.936 | 11.935 | 11.937 | 11.943 | 11.916 | 11.931 |
| Deviat. | 0.013 | 0.015 | 0.012 | 0.009 | 0.031 | 0.014 | |
| Best | 11.958 | 11.960 | 11.957 | 11.959 | 11.947 | 11.956 | |
| Time (s) | Mean | 105.1 | 220.6 | 97.9 | 175.7 | 104.1 | 209.3 |
| Deviat | 11.48 | 71.83 | 15.45 | 40.56 | 14.39 | 72.67 | |
| Investment (M€) | Mean | 257.1 | 257.4 | 256.7 | 256.6 | 256.8 | 256.8 |
| Deviat | 0.51 | 0.48 | 0.53 | 0.42 | 0.61 | 0.43 | |
| NPV (M) | IRR (%) | ctrx | ctry | ndaa | ndba | θ | Tilt | |
| Mean | 67.0 | 11.933 | 40.9 | 27.5 | 6.7 | 11 | - 22 | 5.4 |
| std | 0.49 | 0.019 | 0.78 | 0.56 | 0.74 | 1.52 | 74.2 | 13.0 |
| Cross Area | Fixed losses | Variable losses | Imax | Norm. Price |
| (mm2) | (W/m) | (mW/m/A1/2) | (A) | (€2016 /m) |
| A95 | 0 | 0.714 | 380 | 128 |
| A150 | 6 | 0.435 | 430 | 192 |
| A400 | 24 | 0.192 | 680 | 321 |
| A630 | 34 | 0.123 | 780 | 481 |
| A800 | 50 | 0.086 | 900 | 506 |
| B95 | 0 | 0.833 | 260 | 384 |
| B150 | 6 | 0.500 | 360 | 417 |
| B400 | 8 | 0.172 | 640 | 514 |
| B630 | 10 | 0.111 | 790 | 535 |
| B800 | 12 | 0.086 | 900 | 616 |
| Export cable | Onshore cable | ||||
| Voltage | Section | Capacity | Norm. Cost | Capacity | Norm. Cost |
| (kV) | (mm2) | (MVA) | (€2016 /m) | (MVA) | (€2016/m) |
| 220 | 500 | 250 | 844 | 273 | 232.8 |
| 220 | 630 | 273 | 946 | 297 | 266.0 |
| 220 | 800 | 295 | 1061 | 314 | 299.3 |
| 220 | 1000 | 314 | 1214 | 348 | 367.3 |
| p1: max gener = 100 popul. size = 80 p2: max gener = 250 popul. size = 140 |
Objective function = NPV | Objective function = IRR | Objective function = IRR without local search | ||||
| p1 | p2 | p1 | p2 | p1 | p2 | ||
| NPV (M€) | Mean | 67.10 | 67.14 | 67.02 | 67.16 | 66.50 | 66.87 |
| Deviat. | 0.29 | 0.32 | 0.30 | 0.27 | 0.83 | 0.33 | |
| Best | 67.59 | 67.61 | 67.55 | 67.59 | 67.24 | 67.53 | |
| IRR (%) | Mean | 11.936 | 11.935 | 11.937 | 11.943 | 11.916 | 11.931 |
| Deviat. | 0.013 | 0.015 | 0.012 | 0.009 | 0.031 | 0.014 | |
| Best | 11.958 | 11.960 | 11.957 | 11.959 | 11.947 | 11.956 | |
| Time (s) | Mean | 105.1 | 220.6 | 97.9 | 175.7 | 104.1 | 209.3 |
| Deviat | 11.48 | 71.83 | 15.45 | 40.56 | 14.39 | 72.67 | |
| Investment (M€) | Mean | 257.1 | 257.4 | 256.7 | 256.6 | 256.8 | 256.8 |
| Deviat | 0.51 | 0.48 | 0.53 | 0.42 | 0.61 | 0.43 | |
| NPV (M) | IRR (%) | ctrx | ctry | ndaa | ndba | θ | Tilt | |
| Mean | 67.0 | 11.933 | 40.9 | 27.5 | 6.7 | 11 | - 22 | 5.4 |
| std | 0.49 | 0.019 | 0.78 | 0.56 | 0.74 | 1.52 | 74.2 | 13.0 |
| Source | [15] | [16] | [17] | [9] | [18] |
| Turbines | 37% | 47% | 50% | 46% | 49% |
| Foundation | 25% | 29% | 25% | 23% | 21% |
| Elect. Infr. | 23% | 16% | 15% | 21% | 21% |
| Engineering | 12% | 7% | 5% | 10% | 9% |
| Others (SCADA, decommissioning) | 3% | 1% | 5% |