2D vs 3D tracking in bacterial motility analysis

1.   Introduction

Quantifying bacterial motility is important for a fundamental understanding of processes related to virulence and biofouling such as invasion, chemotaxis, biofilm formation, and other collective behaviors such as swarming [1]–[4] For all of its importance, bacterial motility remains incompletely studied and poorly characterized; even a seemingly simple parameter such as average swimming speed is difficult to find for most species and strains. A database called BOSO-Micro was created in 2021 to catalog known motility data for self-propelled unicellular swimmers, emphasizing the need for data in this growing field [5].

Technical and computational barriers make quantification of bacterial motility challenging. Typical light microscopic techniques, such as phase contrast microscopy, show excellent resolution and signal-to-noise and are thus typically used for tracking individual bacteria. However, in typical microscopy applications the cells are confined to chambers tens to hundreds of µm thick. Errors may be introduced both by the confinement and by the lack of Z-coordinate information. Methods for determining Z position are slow relative to the microorganisms' swimming speed and usually permit tracking of only a few cells at a time [6], although recent computational approaches have permitted inference of Z coordinates from defocusing patterns [7]–[10].

Volumetric techniques, such as digital holographic microscopy (DHM), are emerging solutions to the problem [11],[12]. DHM is a brightfield/phase volumetric technique that permits digital refocusing through sample depths of millimeters. However, its images tend to be noisy, and particle identification remains difficult. Some custom microscopes have been created that yield greater resolution than DHM alone; approaches include multiwavelength imaging and coupling DHM to other imaging modalities [13]–[19]. Other approaches rely upon computational processing for cell identification and tracking [20]–[23].

In all cases, the data volumes required are very high, with a typical size of 0.5 Tb for an XYZ hyperstack of a 30-second recording at 15 frames/s. Most laboratories do not have the computational resources needed to process such data volumes on a regular basis. Most methods to reduce stack size either reduce cell count or resolution. Alternatives to full XYZ reconstruction, such as fitting holograms to scattering models [24], limit stack size but are at least as computationally intensive as reconstruction if the cells are not spherical.

Of fundamental importance to quantifying motility is cell tracking via instantaneous or average speeds, total distance/displacement and cell trajectory or turn angles. Since bacterial motility is stochastic in nature, tracking either large numbers of cells or cells for long time periods is desirable to generate robust statistics. In general, most high throughput methods available for cell tracking have been developed for 2D tracking often with less reliable extensions to 3D tracking. This is due to a few factors. Many microscopes have a single plane of focus. A high-resolution objective provides images that demonstrate high signal to noise. While DHM data can provide 3D information on cell locations in unconstrained volumes, processing this data is computationally intensive and pre- and post-processing of data remains unique to the dataset of interest prohibiting a “black box” high throughput approach.

The purpose of this study was to develop methods to determine key motility parameters in free-swimming bacteria while minimizing computational intensity. Rapid tracking of thousands of 10 µm organisms has been shown by Sheng et al. [25],[26] Single nonpigmented bacteria represent a “no man's land” where tracking requires manual tracking or computationally intensive procedures such as extensive denoising [27] or fitting to non-linear scattering models [28]. Depending on the dataset and signal-to-noise ratios, different tracking algorithms may confuse particles of interest with noise resulting in false positives and erroneous tracks. Tracking processes that work for objects of known size and shape may not work with motile particles of a similar size. A recent review details different methods of cell tracking of DHM data illustrates that methods tend to alter based on cell size [29]. In both these cases, it is important to identify whether computer generated tracks match the dataset. The method shown here allows researchers to make these comparisons and provide quality assurance for bulk processing. With this goal in mind, we make no attempt to quantify specific motility behaviors of the organisms in this study. We are merely interested in ascertaining what localization errors arise when tracking non-labeled cells ~1–2 µm in length. We use DHM to record from volumes of 263.25 x 263.25 x 1200 µm in X, Y, and Z respectively, then track individual cells and ensembles of cells in both XY projections and full XYZ hyperstacks. The errors introduced by projecting the motion into XY are quantified for free-swimming organisms as well as those near solid surfaces. We used two test organisms: Vibrio alginolyticus and Shewanella putrefaciens. Vibrio sp. And S. putrefaciens swim by means of a single polar flagellum and “reverse and flick” [30],[31] motility. Vibrio represents some pathogens of great importance to human health (V. cholerae, the causative agent of cholera), as well as many species that are less dangerous to humans but which are pathogenic to marine organisms such as coral and fish. The role of motility to virulence in V. cholerae is intriguing, as non-motile mutants show 10-fold less pathogenicity than the wild type [32],[33]. S. putrefaciens is a recently discovered fish pathogen [34],[35] (and occasional opportunistic human pathogen [36]) for which the role of motility in virulence has not been explored.

We find that in the case of determining average speeds that 2D tracking is generally sufficient. This is due to the formulaic and empirical nature of identifying 3D coordinates and calculating 3D speeds. However, we also show that knowledge of relative position in Z is valuable with the subset of bacterial motility as it relates to a solid surface. Not only are bacteria influenced by the surface presence, speeds calculated by the surface should be omitted when averaging unconstrained swimming speeds.

2.   Materials and methods

2.1.   Culture conditions

An overnight culture of Vibrio alginolyticus YM4 (gift of R. Stocker, MIT) was diluted into BD Difco™ Marine Broth (Thermo Fisher Scientific) and incubated at 30 °C until reaching an OD₆₀₀ reading ~0.2. Cultures were grown aerobically in 1 mL HARV bioreactors (Synthecon, Houston, TX) in both the vertical orientation (simulated microgravity) and horizontal orientation (normal gravity). Bubbles were removed to eliminate the possibility of turbulence. A semi-permeable membrane along the back of the bioreactor provides oxygenation. The chambers were rotated in both configurations at 20 rpm for five hours before microbes were removed. OD₆₀₀ readings upon removal corresponded to the mid-exponential growth phase. Vibrio were then diluted into 1 to 100 mL motility medium (300 mM NaCl and 5 mM MgCl₂ (Macron Fine Chemicals), 50 mM Hepes and 5 mM glucose (Sigma-Aldrich)). Motility imaging occurred directly after removal.

Shewanella putrefaciens (gift of Ken Nealson of Southern California) was maintained in Luria Broth. Overnight cultures at an OD₆₀₀ reading of 0.3–0.4 were placed into a sealed sample chamber containing minimal medium for recording.

2.2.   Holographic microscopy

The microscope used was a custom Mach–Zehnder design as described previously [37],[38], where high-NA objectives were placed in both the science and reference beams. The microscope objectives used for the recordings shown here were Mitutoyo Plan Apo 50x long working-distance objectives with a numerical aperture (NA) of 0.55. The objective is infinity corrected so an achromatic field lens of 200 mm focal length is used to form the image on the CCD. Illumination was from a single-mode 405 nm fiber-coupled diode laser (Thorlabs); diffraction-limited resolution is estimated at l/2NA = 0.37 µm in XY and 2l/(NA)² = 2.7 µm in Z.

Data acquisition was performed using either Koala (LynceeTec, Lausanne, Switzerland) (Vibrio dataset) or a custom open-source software package, DHMx [39] (Shewanella dataset). Recordings for the Vibrio dataset were captured at approximate 7 fps for a total of 120 seconds. Recordings for the Shewanella dataset were captured at 15 fps for 60 seconds. Reconstruction in phase was performed using the angular spectrum method [40] using custom Fiji plug-ins as previously described [41]. Phase reconstructions made use a reference hologram to remove noise [42]; this reference hologram was the median of all holograms in the recording. The lateral field of view was 263.25 x 263.25 µm for 2048 x 2048 pixels, and the axial z-spacing was chosen to be 2 µm based upon the particle size and nominal axial resolution of the system.

2.3.   Data processing and analysis

All manipulations were performed in FIJI [43]. Reconstructions for both samples were performed in phase. The Vibrio dataset required no further manipulation. The Shewanella dataset required median subtraction after phase reconstruction to remove excess noise.

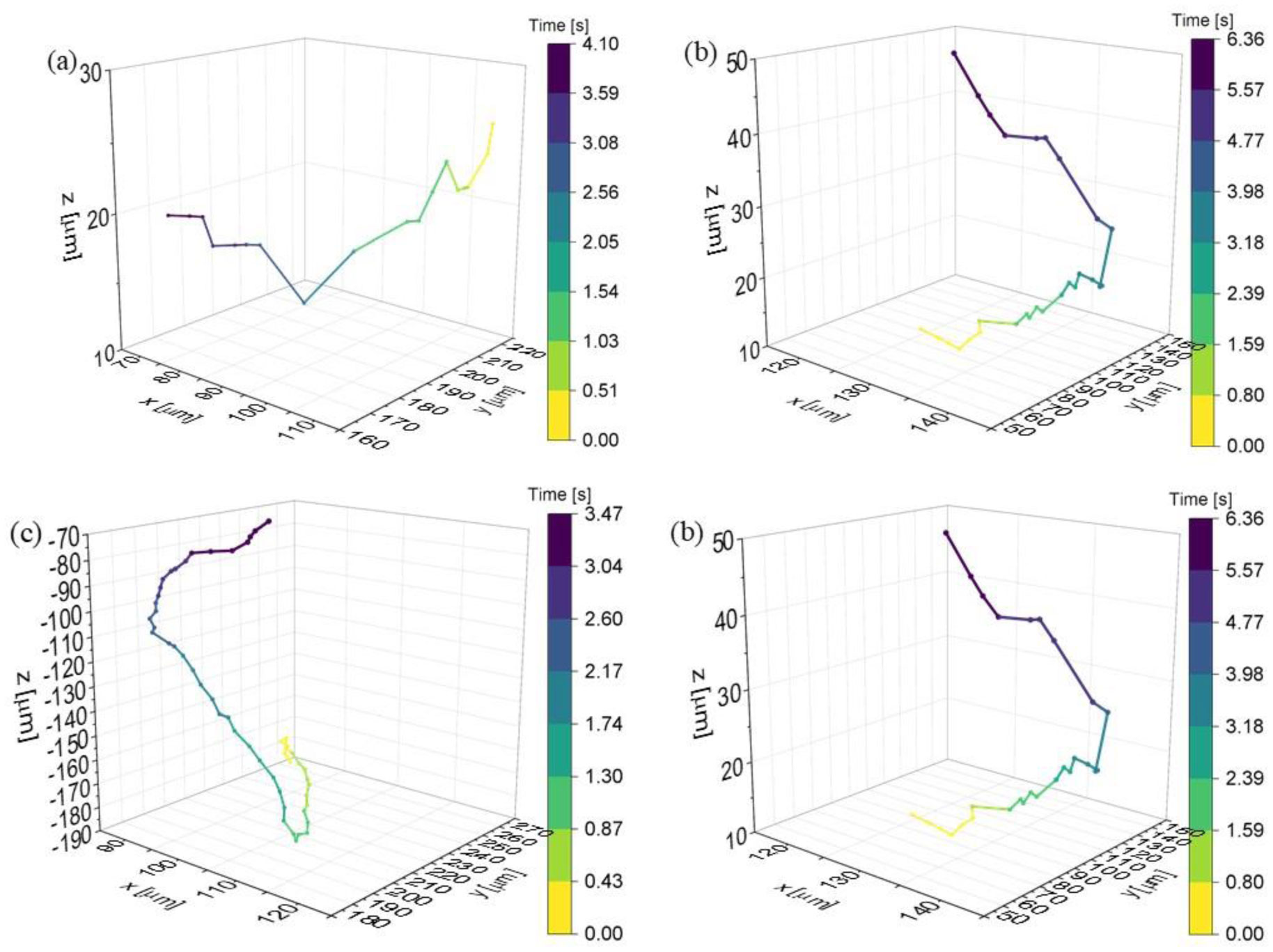
XYZT tracking was performed by creating an XYZT hyperstack and cell body center positions were recorded in Excel after manually focusing through Z. An example of this process can be seen in Figure 1. To limit the size of the hyperstack (hyperstacks constructed in this study average ~15Gb in size), we used hyperstacks with a wide range in z (~100–300µm) for ~15 time points. Microbes were selected, tracked, then new hyperstacks were constructed with the same XYZ parameters for the next set of time points. In addition to Figure 1, our supplementary videos show the appearance of Vibrio (Supplementary Video 1) and Shewanella (Supplementary Video 2) as they swim in and out of focus. Analysis, including instantaneous and average speeds, was done in Microsoft Excel. Plots were constructed using Origin.

3.   Results and discussion

3.1.   Comparison of 2D vs. 3D phenotypes and speeds

Vibrio and Shewanella cells were tracked in 3D and their traces are shown in Figure 1. The Vibrio cells (Figure 1a) had an ~8 µm and ~40 µm (Figure 1b) displacement in Z, respectively. The Shewanella cell in (Figure 1c) had ~60 µm displacement in Z, while the cell in (Figure 1d) had a ~70 µm displacement. The traces were limited to the time the microbe was in the field of view, which ranged from 3.5 to 6 seconds. The color bars indicate the progression of the microbe through time. The traces connect the observed data points with no smoothing. The Vibrio cells appear to have bigger jumps in their traces due to the lower framerate while the Shewanella cell traces were smoother due to both a faster framerate and no dropped frames. Although more cell traces were recorded, we have chosen these for both the length of time tracked and to illustrate cells that moved little in Z vs. longer periods in Z.

For the above cell traces, we calculated instantaneous speeds. Speeds were calculated using Equation 1:

Where v_x was calculated as the change of the center of the cell body from frame to frame in the X-direction. Similar calculations were performed in the Y and Z directions. These speeds were then used to generate XY and XYZ speeds using Equations 2 and 3 respectively:

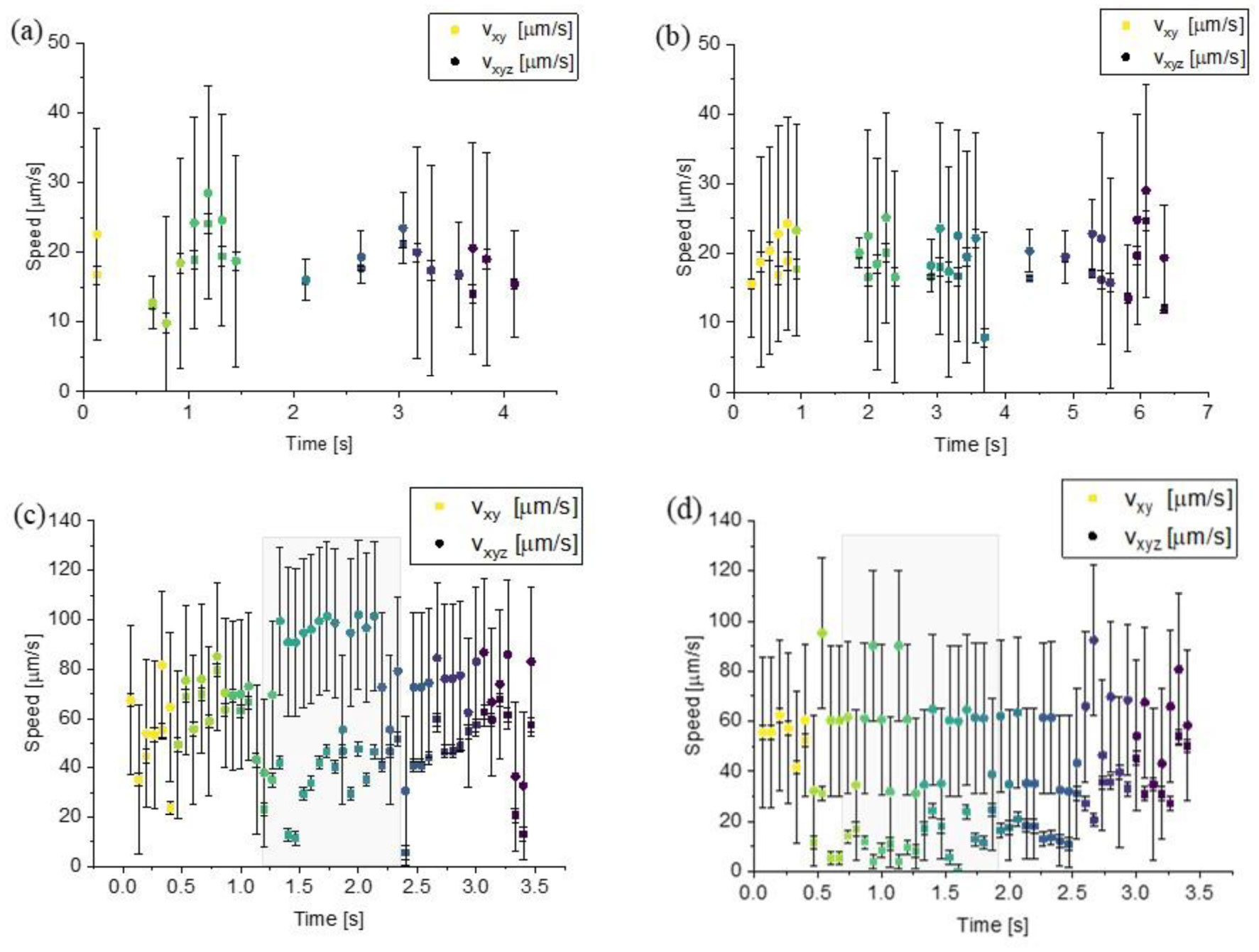
We calculated instantaneous changes in speed from frame to frame and plotted these vs. time as seen in Figure 2. The error bars illustrate the uncertainty associated with tracking cell body centers. In the X and Y directions, the associated uncertainty comes from the total pixels divided by the field of view. However, the Z-positions result in a larger uncertainty based on the Z-distance reconstruction of 2 µm. These uncertainties were used to calculate speeds by dividing by the change in time which varied between the Vibrio and Shewanella datasets.

These plots show that accounting for movement in Z influences speeds both formulaically and empirically. The way speeds are calculated in Equations 2 and 3 results in either v_xy = v_xyz if v_z = 0 or v_xy < v_xyz if v_z > 0. We can see this effect in Figure 2. In all cases, as predicted, v_xy ≤ v_xyz. Especially when considering the uncertainty introduced when calculating v_xyz, in most cases instantaneous speeds are within the projected uncertainty. However, there are exceptions to this in Figure 2c-d, illustrated by the shaded regions. These regions show that v_xyz speeds increased to ~90–100µm/s. The v_xy speeds fell well below these values even when considering uncertainty. When compared with the cell traces in Figure 1c-d, these also correspond to substantial movement of the cells in Z. Together, these plots show that for fast-moving cells traveling through Z (speeds greater than ~90 µm/s), the changes in Z should not be neglected.

When tracking cells over long time periods, often it is desired to calculate average speeds. These averages are summarized in Table 1.

From the Vibrio dataset, the average speeds between v_xy and v_xyz were within projected uncertainty regardless of small or large displacement in Z. For the Shewanella dataset, although v_xyz appears much larger than v_xy, these average speeds were also nearly within projected uncertainty (~± 30 µm/s) due to the faster framerate. The Shewanella cells had a large displacement in Z which also makes this finding interesting.

A common method to simplify cell tracking is to construct 2D projections from 3D reconstructions, removing fine Z coordinate information. They may be constructed using FIJI. For example, using the max project function takes the maximum intensity value within a specified Z-range for each XY position. Repeating this process through time can generate high signal XY traces, however, in the process, Z-coordinate information is removed. Additionally, cell centers can be obscured as this method might occasionally project noise instead, especially for cells of the size used in this study. Other complications arise when cells trace or cross paths in Z, a problem that is exacerbated with larger cell sizes or crowded datasets. Taute et al. [44] also compared differences between 2D projections and 3D speeds. However, they estimated a particle's Z location using a diffraction pattern library ignoring localization errors and acquisition frequency. In this work, we have identified the source of these localization errors and shown how these errors influence average 2D and 3D speeds.

In the following, we discuss further the empirical uncertainty associated with the Z-coordinate. As others have noted [45],[46], reconstructions result in point-spread functions (PSFs) (or volume-spread functions in XYZ). Without any post-processing, PSFs cause microbes to appear with a larger thickness in z than the cell thickness would indicate. For example, Vibrio cells are ~2 µm in length with ~0.5 µm thickness. PSFs can cause the length or thickness to appear much longer resulting in apparent lengths/thicknesses of ~4–6 µm (Figure 4). Reconstructing at smaller Z intervals does not resolve this issue. Post-processing, such as deconvolution, can resolve ambiguity of cell position but can result in lost cell shape information due to thresholding and may be computationally intensive. In addition, although it is routine in fluorescence microscopy, deconvolution remains difficult in DHM, with only a few reports published [47],[48] and no implantation in standard image processing software packages. This effect can be quantified by examining changes in X, Y, and Z displacements. In the case of the Shewanella cell, X and Y displacements range from 0 to 5 µm with an associated uncertainty of 0.13 µm. In contrast, Z displacements range from 0 to 6 µm with an associated uncertainty of 2 µm. For a fast-swimming microbe, changes in Z are greater and therefore cause associated v_z speeds to be subject to even more uncertainty.

Motility analysis is also highly dependent on framerate. Ideally, higher framerates are desirable for capturing precise movement. However, in practice, high framerates result in large datasets that are made even larger after the reconstruction process. Acquisition rates vary between DHM set-ups. In the datasets used in this study, one was acquired at a near constant framerate of 15 fps while the other had dropped frames resulting in an acquisition rate of approximately 7 fps. When comparing the differences in 2D and 3D tracking, the impact of the framerate at which the data were acquired cannot be neglected from both quantitative and qualitative perspectives. We have shown above how the frame rate influenced instantaneous and average speeds. Framerate also impacts qualitative explanations of microbial behavior. This can be seen from the course traces in Figure 1. Figure 1a-b show sharp changes trajectory while Figure 1c-d, in contrast, show smooth swimming trajectories. Different studies have coped with lower framerates by introducing smoothing functions [45], however, since bacterial movement can be impacted by a variety of environmental factors, these smoothing methods must be treated with caution. In this study, the higher framerate ultimately resulted in large uncertainties in v_z compared to v_x and v_y. This finding could suggest that lower framerates are desirable as larger changes in time blunt the impact on v_z. However, this should also be treated with caution. For instance, consider the physical and mechanical properties of the microbe. Microbes with a single polar flagellum such as microbes in this study, can execute the “run-reverse” or “run-reverse-flick” phenotype. If a microbe is moving fast enough, this behavior might go completely unobserved with a low framerate.

3.2.   Importance of relative positions in Z–surface behavior

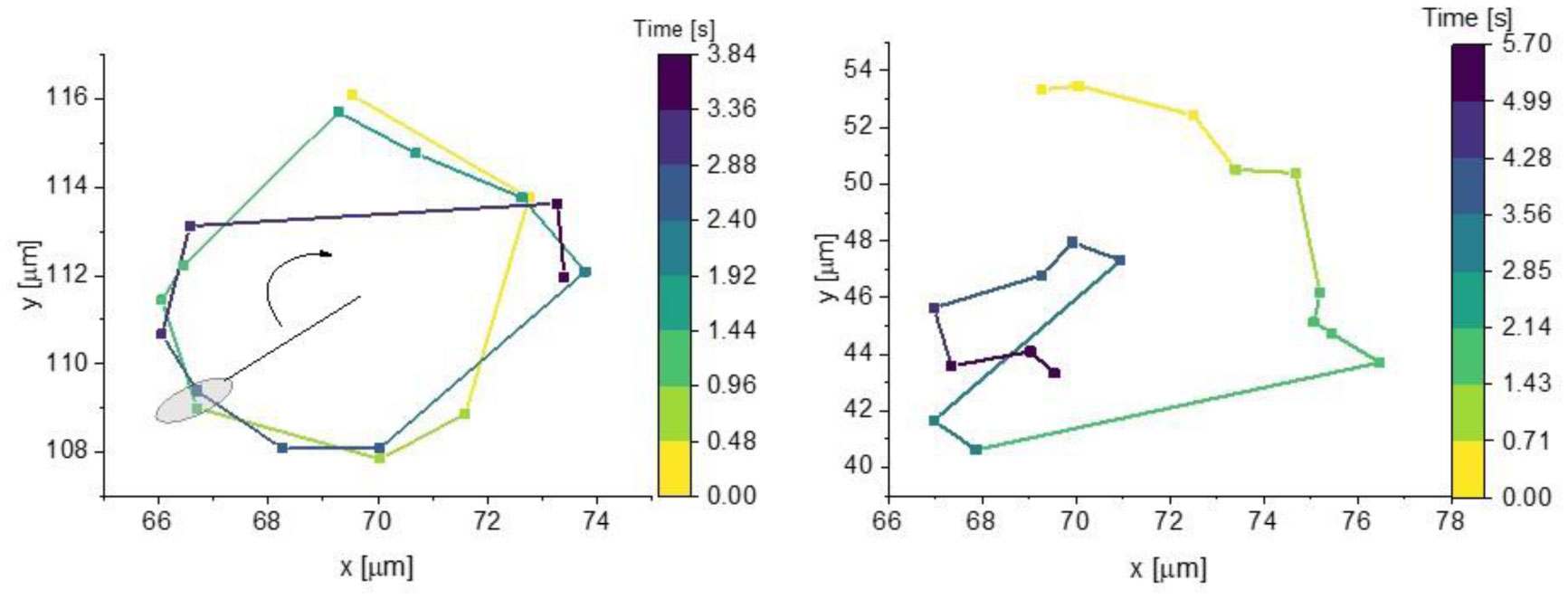
3D tracking of cells allows visualization of dynamic cell behavior by surfaces. At best, a 2D projection provides motility behavior either on a surface or at a set distance from the surface but does not show dynamic motility changes as a cell approaches a surface. Theoretical models predict cell motility to change as cells approach a surface, namely that speeds would decrease, and trajectories may shift from straight swimming to circular swimming as cells are subject to surface forces [49],[50]. In some cases, cell flagella can adhere to surfaces resulting in fast-moving tight circles [51]. Figure 5 shows both phenomena as we observed using DHM. Although we were unable to resolve flagella in this study, the presence of the flagella can be inferred based on the movement [52] and the flagella length is within known values of Vibrio flagellar length [53].

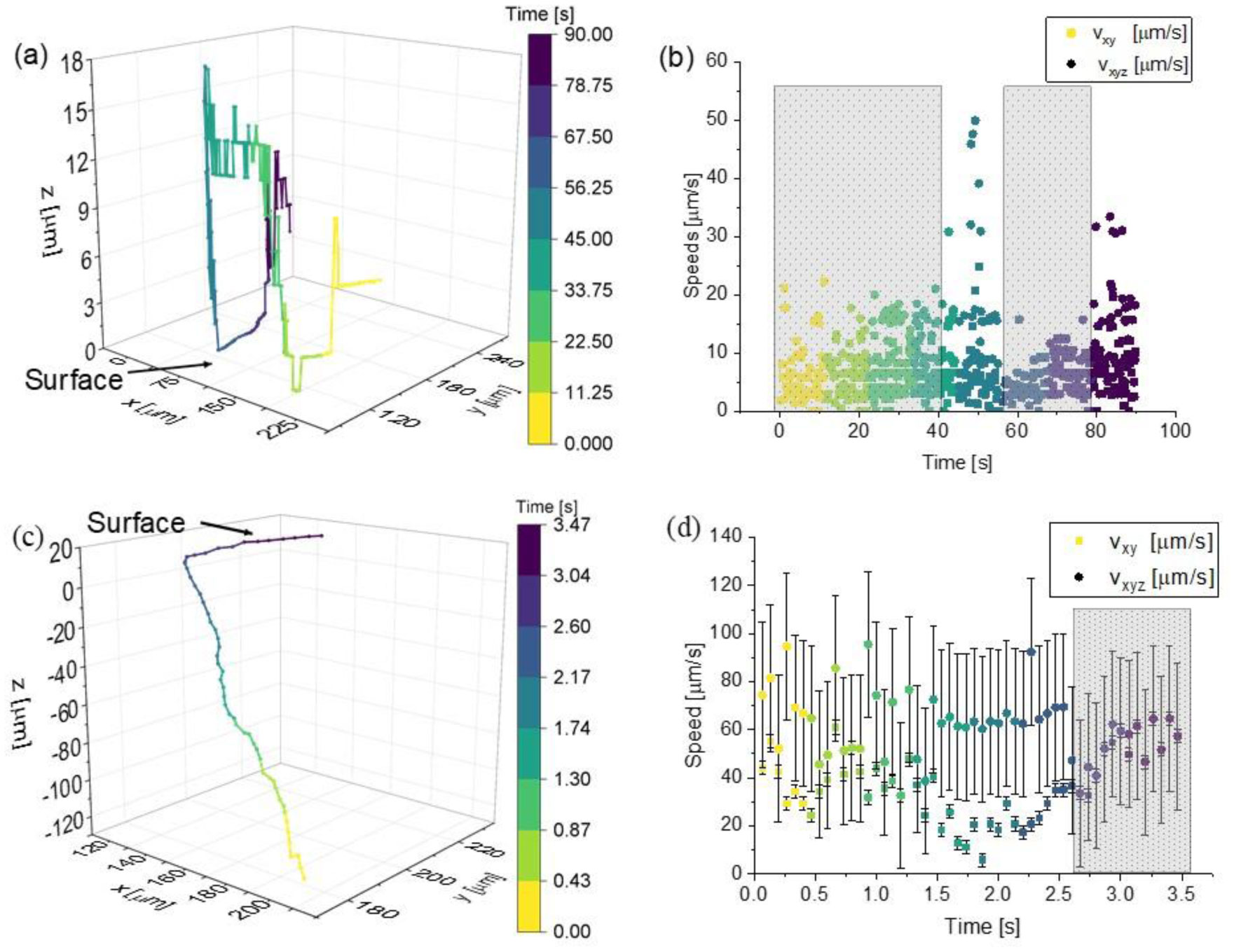
In this work, we tracked a Vibrio and Shewanella cell (Figure 6 a and c) moving in an unconstrained volume to a surface. Resolving the precise location of a surface in Z for a surface using DHM remains challenging. In this study, the surface plane was approximated using a few metrics. Analysis of XYZT hyperstacks shows microbes coming into and out of focus while scrolling through Z (Refer again to Supplementary Video 1 and 2). However, once the field of view passes through the surface, microbes no longer come into and out of focus, rather the cell Airy rings continue to enlarge. Taking this information together provides a rough estimate of the surface location. A second metric is the presence of either non-motile cells or cells exhibiting the circular phenotypes (pictured in Figure 5) or moving slower. This allowed an estimate of the surface location within ~2 µm. Molaei et al. [54] also reported a confidence within 2µm, for their work. This distance is subject to error based on the reconstruction distance as stated previously. Interestingly, the reduction in motility due to surface effects can result in organisms remaining within the field of view for longer residence times. The microbe shown in Figure 6a was in the field of view and able to be tracked for ninety seconds. Figures 6b, d show instantaneous speeds with the color map showing how the instantaneous speeds visually correlate with position. The shaded boxes correspond to surface regions. It is important to note that recording v_xyz provides important information regarding the cell phenotype. Figures 6b, d shows how v_xy and v_xyz overlap as expected when v_z = 0. Since there is no change in Z along the surface, this is to be expected. However, at distances away from the surface, v_z is much higher. In fact, in 6d, v_xyz > v_xy even considering the uncertainty introduced by the Z reconstruction distance.

These results show that calculating and including v_z in v_xyz is important for quantifying surface behavior. Goto et al. [49] and Bianchi et al. [55] showed a correlation between speed and position from the surface. To understand these behaviors in greater detail, a precise understanding of how speeds of microbes dynamically change as they approach a surface is needed along with a thorough understanding of the uncertainty of these speeds when matching these behaviors with theoretical models. For instance, Goto et al. [49] predicted that for mono-flagellated species, swimming speed by a surface is influenced by flagellar length. To categorize the difference in these speeds, researchers should consider what resolution and framerate are necessary to study these behaviors to minimize localization uncertainty. Additionally, our results show that when considering overall average speeds, instantaneous speeds calculated while cells are ~10 µm of the surface should be removed from unconstrained volume free-swimming statistics.

Quantifying microbial behavior next to surfaces has been approached in different ways. An early method of studying surface behavior used a microscope with a moving chamber to record positions of microbes but with a limited field of view and difficulty in remaining fixed on microbes of interest [56],[57]. Bianchi et al. [58] has approached the difficulty of quantifying surface behavior in E. coli by using an in DHM set-up with multiple wavelengths to obtain volumetric information. To control for known distance of cells from the surface, they used optical tweezers to place cells within 10 µm of the surface. The released cells were then caught by the surface and exhibited circular swimming. In this way, they were able to measure the pitch of the cell against the surface. While our experimental set-up does not have this level of precision, holograms and in turn their reconstructions, provide a comprehensive picture of the qualitative behavior of many cells with both a large field of view and depth of field.

Microbes exhibit different phenotypes depending on their environment such as: an unconstrained volume [45], a narrow channel such as a microfluidics device [59],[60], along solid surfaces [49],[61], or non-solid sufaces [55],[62]. Depending on the cell type and number of flagella, cells can exhibit “run and tumble,” “run-reverse” or “run-reverse-flick” in unconstrained volumes [63]. Cells that move from an unconstrained volume to swim along a solid surface may be captured by surface forces. If they are unable to break away from the surface, they may eventually transition to a sessile or non-motile state. If free-swimming cells sense these non-motile cells through chemotaxis or quorum sensing, they might join these cells to form biofilm [60],[64]. Biofilm is often associated with increased virulence and pathogenicity. Accounting for Z movement could shed more light on mechanisms for biofilm formation.

Interestingly, surface behavior itself can refer to many different phenotypes. In this study, we have shown the behavior of microbes in an unconstrained volume approaching a solid surface. However, microbes have also been shown to move along solid surfaces, such as agar plates. In these instances, cells grow lateral flagella or pili and “crawl” along the surface either by swarming, gliding or twitching [65],[66]. While these phenomena are important to study as well, by tracking colony movement along plates, these studies circumvent the immense difficulty associated with 3D tracking.

4.   Conclusions

In our work, we have used DHM to show the importance of the Z coordinate. Many motility studies have used 2D tracking to report average speeds at various temperatures and changes in speed due to environmental factors such as chemoattractants. Although v_xyz is generally either equal to or greater than v_xy, we have demonstrated overall average speeds cell speeds are generally within empirical uncertainties. Fast moving cells (cells moving faster than > 90 µm/s) generate more uncertainty based on the Z resolution computationally available. However, there are specific cases where 2D tracking is not sufficient, one of those being in the study of dynamic surface behavior. Surface behavior lowers speeds making any averages that include these speeds artificially low. Finally, it is important to consider and carefully account for framerate when recording motility information.