1. Introduction
When the Fisher hypothesis is supported, the asset is a good hedging tool against inflation, which is also one of the reasons scholars often discuss whether the Fisher hypothesis is supported.1 Fisher hypothesis (Fisher, 1930) suggests that asset prices can reflect the change in inflation rate; when inflation rate changes, the nominal rate of return will adjust correspondingly while real rate of return will remain unchanged. Thus, there is a positive correlation between the nominal rate of stock return and inflation, but there is no correlation between the real rate of stock return and inflation. However, Nelson (1976) and Fama and Schwert (1977) find that there is a negative relationship between stock return and inflation in the United States. To explain this puzzling phenomenon, Fama (1981) puts forward the proxy hypothesis that states the following: company's stock price reflects its profit level, the real stock return is positively related to real economic growth, and increase in inflation represents a drop in real economic growth and will simultaneously lower real stock return. Thus, stock return and inflation are both negatively affected by real economic growth; such negative correlation is only a "proxy" presentation of the positive correlation between stock return and real economic growth.
1 The Federal Reserve (FED) always treats combating inflation as the top priority by adjusting interest rates to curb inflation, which has then created a significantly negative causal relationship between inflation and economic growth in the United States.
Based on the classical dichotomy as an example, inflation is listed as a nominal variable and should only be impacted by real variables but not the other way around. Hence, Fisher's (1930) interest rate equation implies that real asset return (such as real stock return) is only affected by real variables and not by expected inflation.2 However, empirical studies have found that inflation can indeed affect real variables. For example, Nelson (1976) finds that there is a significantly negative correlation between real stock return and inflation; Khan and Senhadji (2001) find that a strong currency system has a negative impact on economic growth. Regarding whether Fisher hypothesis is supported with a change in time, recent studies such as by Lee (2000) argues that Fisher hypothesis is not supported and that both positive and negative correlations exist between inflation and stock return. However, Katzur and Spierdijk (2013) and Everaert (2014) suggest that Fisher hypothesis is supported, whereas Ozcan and Ari (2015) argue that Fisher hypothesis is only partially supported. A comparison of related literature can be found in Appendix 1.
2 Fisher argues that real interest rate is affected by real factors but not expected inflation; nominal rate and expected inflation will adjust in a 1:1 ratio.
Also, there are also many studies on Fama's proxy hypothesis, which are derived from the discussion of whether Fisher hypothesis is supported. Among the related studies, the findings by Geske and Roll (1983) are consistent with the phenomenon of debt monetization and support the proxy hypothesis. Kaul (1987) reveals that the direction of monetary policy that a government adopts will change the correlation between inflation and real stock return, thereby supporting the proxy hypothesis. Cozier and Rahman (1988) point out that the Canadian data support Fama's proxy hypothesis, while Lee (1992) reveals that the American data support the proxy hypothesis.3 Gallagher and Taylor (2002) find that under supply crisis, a significantly negative correlation exists between inflation and stock return and that under demand crisis, no significant negative correlation exists between inflation and stock return. Gallagher and Taylor (2002) also confirm that the quarterly data of the United States support the proxy hypothesis. Kim (2003) tests the correlation between stock return and inflation in Germany and reconfirms that the proxy hypothesis is supported. Madsen (2005) argues that supply-related factors are the supporting factors of the proxy hypothesis that should not be neglected.
3 Real stock return is nominal stock return minus expected inflation, and real interest rate is nominal interest rate minus expected inflation (based on one-month Treasury Bill), which is an estimate derived from the real inflation using the simple Kalman filter method.
There are also many related studies that reject the proxy hypothesis. For example, the empirical results of Balduzzi (1995) that explain the negative correlation between stock return and inflation do not support the proxy hypothesis. Caporal and Jung (1997) employ the quarterly data in the United States to construct an empirical model; their results reveal that real economic growth cannot explain the correlation between inflation and real stock return using the proxy model. Schmeling and Schrimpf (2011) adopt the linear pool model, the VAR model, and the internal and external validation of a predictive model to empirically verify the data of different countries such as Germany, Britain, the United States, France, Italy, and Japan. Schmeling and Schrimpf reveal that the existence of money illusion leads to the failure of the proxy hypothesis.
As seen from the above studies, the majority of empirical studies are based on time series data in a linear model framework that employs different types of study subjects. Empirical results of both that support and reject the Fisher hypothesis, and the Fama's proxy hypothesis exist, indicating that variances in study subjects, study period, and variable selection can perhaps influence the conclusion of whether the Fisher hypothesis and the Fama's proxy hypothesis are supported. As far as data characteristics are concerned, there are relatively few studies in the past that adopt panel data, but a country or multiple countries were studied in the empirical model, which may have possibly neglected the important cross-sectional information (Sarel, 1996).
Under global integration, a government can implement economic policies via monetary market and foreign exchange market. Interest Rate Parity points out there would be spillover effects when a central bank adjusts its nominal interest rate. The spillover effects debates the Fisher Hypothesis. Meanwhile whether the hypothesis is valid would be affected by foreign exchange market between countries. Therefore only examining the hypothesis in individual country but ignoring the interactions of foreign exchange markets among countries could induce testing errors. This gap induced Westerlund (2008), Badillo et al. (2011), Everaert (2014), Ozcan and Ari (2015) etc. to use the cross sectional analysis to test the hypothesis. In addition, panel data that consist of cross-sectional and time series data not only can track the dynamic relationship among variables from time series data but can also present cross-sectional characteristics. Panel data is superior in empirical research, for example, it allows for larger number of observations facilitating a high degree of freedom and efficiency in estimation. The superiorities of cross sectional analysis can help us to explain the puzzle in Fisher hypothesis.
Regarding empirical methodology, some studies may not have considered the non-linear relationship among variables. For example, Graner and Terasvirta (1993) suggest that most macroeconomic variables have nonlinear characteristics in that the relationship between real stock return and real economic growth may also be nonlinear. Kim and Ryoo (2011) and Tsong and Lee (2013) adopt the nonlinear model namely, threshold vector error correction model and quantile analysis, respectively, to verify the Fisher hypothesis. Conclusions of both in favor of and against the Fisher hypothesis are obtained. Both studies believe that whether the Fisher hypothesis is supported depends on the conditions defined; however, no further investigation was conducted to elaborate the reasons why the Fisher hypothesis was rejected. Based on these findings, it is proposed that the different results in previous studies may be caused by the lack of cross-sectional data from multiple countries and non-consideration of the nonlinear relationships, thereby restricting the research content from being comprehensive. Therefore, the roles of these factors should be clarified to see if they interfere with the establishment of the Fisher hypothesis and whether Fama's proxy hypothesis is supported when the Fisher hypothesis is rejected. These related topics should all be incorporated into a discussion such that the research would become more comprehensive, which is indeed the motive of the present study.
On the other hand, as panel data consist of cross-sectional and time series data, the present study adopts the estimation procedure with bias correction called the threshold dynamic panel data model (hereinafter referred to as TDPM) proposed by Chen and Lin (2010) to reexamine whether the Fisher hypothesis and Fama's proxy hypothesis are supported. Under regimes of different economic growth, a TDPM is first developed for real stock return and general (expected and unexpected) inflation to confirm the nonlinear relationship between the two variables. Then real economic growth is incorporated into the TDPM to verify if the correlation between real stock return and inflation of different nature will change. The present study will reconfirm whether the Fisher hypothesis and the Fama's proxy hypothesis are still supported under the TDPM and if yes, under what kind of economic regime. Also, the present study also explores if data from different country clusters will influence the establishment of the Fisher hypothesis and Fama's proxy hypothesis, which is the aim of the present study.
The structure of the present study is presented as follows: 1. Introduction, 2. Research method and data description, 3. Empirical result analysis, and 4. Conclusions.
2. Research Method and Data Description
2.1. Research method
Panel data that consist of cross-sectional and time series data not only can track the dynamic relationship among variables from time series data but can also present cross-sectional characteristics. Panel data is superior in empirical research, for example, it allows for larger number of observations facilitating a high degree of freedom and efficiency in estimation.
As the empirical data collected in the present study has the characteristics of time series, the adoption of dynamic setup is relatively reasonable. The TDPM is regarded as dynamic because a lagged dependent variable is included as an independent variable; when estimated by the OLS method, the interference of residual variance will lead to biased estimation results. The common practice is to employ GMM (generalized method of moment), the estimation method adopted in Arellano and Bond (1991) or Arellano and Bover (1995). As the relationship among the variables discussed in the present study may be nonlinear, if the nonlinear method is adopted to estimate the TDPM, the correction process of the original bias in the TDPM will become more complicated. Thus, Hensan (1999) abandoned the dynamic setting and only constructed a static panel data model to lower the complexity of the empirical analysis.
The topic of how to accurately construct the so-called TDPM has attracted many scholars to try adopting different statistical and measurement theories to overcome the complex correction process involved. For example, Chen and Lin (2010) expand the research of Hensan (1999) and adopt a dynamic setting in the TDPM to verify, under fixed effect coefficients, if threshold effect exists in cigarette consumption behavior at different income levels among the different states in the United States of America. Chen and Lin find that the United States can be divided into three economic growth regimes: low, medium, and high and that the demand elasticity varies among the different regimes. The unique feature of the TDPM in Chen and Lin is the adoption of the bootstrap method in correcting the biases generated in the dynamic model with small sample size.4 Small sample size is emphasized because when the number of cross sections (N) is not big enough to track dynamic data, GMM estimation will not be sufficient to fully correct biases. Rather, this kind of model applies to a limited number of cross sections and unbalanced panel data tracking.5 In Chen and Lin (2010), the TDPM retains the unique coefficient value of each cross-section (such as fixed effects), 6 which is one of the merits of the TDPM. Another merit highlights that when the number of cross sections is limited, the TDPM can still fulfill the estimation and correction processes of the empirical model. Such a merit is perfectly applicable to the present study sample, that is, a limited number of stock markets in the world, which is indeed why the present study follows the model in Chen and Lin (2010).
4 If GMM is adopted in TDPM to correct biases caused by residual variances, a larger number of cross sections (N) must be adopted as well. The data employed in the present study is related to stock markets and there is only a limited number of countries that have stock markets. Therefore, the present study falls into the situation of having limited number of cross sections.
5 Alvarez and Arellano (2003) point out that the biases estimated by GMM in the simple TDPM will decrease at the ratio of 1/N.
6 Substituting the group average y∗i,t=yi,t−¯yi., fixed coefficient will be eliminated and does not exist in the transition model.
The empirical method and model framework of the present study are summarized as follows:
In Chen and Lin (2010), the TDPM is constructed based on a dual-regime example, and equation (1) is set up as follows:
|
yit=αi+(β1yi,t−1+xitη1)I(qit−d≤γ)+(β2yi,t−1+xitη2)I(qit−d>γ)+eit
|
(1)
|
where the cross section i =1~N and time t =1~T, yit is the dependent variable, xit is the independent variable (vector), qit-d is the threshold variable, and γ is the threshold value. The optimal threshold equation is determined by the sum of squares of the least residuals. I(qit−d≤γ) moreover, I(qit−d>γ) are pointer variables that distinguish the upper and the lower regimes, respectively (value is 1 or 0); when satisfied, the pointer variable equals to 1. Otherwise, it equals to 0. eit is an interference term, and η1,η2 are estimated parameter matrix of each respective regime. At a given threshold value, the least squares method is employed in the TDPM to calculate the residual sum of squares, and then the optimal threshold γ is calculated from the minimum residual sum of squares; all parameters in the regime (before bias correction) are then estimated. Due to dynamic setup and nonlinear framework, the estimated results from equation (1) may be biased and must be corrected. Thus, bootstrapping may further be applied to re estimate the TDPM model to obtain enough number of samples and statistics for bias correction.
In addition, at a given threshold value, ˆβ1(γ),ˆβ2(γ) and ˆη1(γ),ˆη2(γ) are estimated under fixed effects; then all ˆαi(γ) and residual error, ˆeit(γ) are calculated; and for each cross-section i, bootstrapping is applied to generate the exogenous variable and residual; further bootstrap sample can be generated as follows:
|
y∗it(γ)=ˆαi(γ)+(ˆβ1(γ)y∗i,t−1+x∗itˆη1(γ))1(qit−d≤γ)+(ˆβ2(γ)y∗i,t−1+x∗itˆη2(γ))1(qit−d>γ)+e∗it(γ)
|
At each given threshold value, the estimation equations of β1 and β2after bias correction are respectively generated as follows:
|
ˆβ1B(γ)=2ˆβ1(γ)−1BB∑b=1β∗1,b(γ),
|
|
ˆβ2B(γ)=2ˆβ2(γ)−1BB∑b=1β∗2,b(γ),
|
where the bias-corrected transition parameter is defined as:
|
ˆγB=argminγ∈Γ˜S′NT(γ)
|
(2)
|
where
|
˜S′NT(γ)=N∑i=1T∑t=1[˜yit−(ˆβ1,B(γ)˜yi,t−1+x∗itˆη1,B(γ))1(qit−d≤γ)−(ˆβ2,B(γ)˜yi,t−1+x∗itˆη2,B(γ))1(qit−d>γ)]
|
For detailed calculation and proof, please refer to the text in Chen and Lin (2010).
2.2. Threshold model definition and description
The variables in the present study are defined as follows: dependent variable is the real stock return (rate) (RST); independent variables are general inflation (PI), which is sub-divided into two other independent variables: expected inflation (PI_E) and unexpected inflation (PI_U); and another real variable is real economic growth (RGY). Different values are assigned to these independent variables to facilitate understanding of how these variables affect real stock return. The top priority of the present study is to verify the Fisher hypothesis and Fama's proxy hypothesis. Also, the study adopts real economic growth as the threshold variable that serves as a proxy variable for the business cycle because it not only reflects the extent of economic change, but can also simplify the relationships among high inflation, low inflation, high economic growth, and low economic growth. For example, a regime of high real economic growth means that nominal economic growth is higher than inflation in the regime, whereas a regime of low real economic growth means that nominal economic growth is lower than inflation in the regime. Also, the optimal threshold generated from endogenous search in the model is more conducive to our understanding of what the critical points are in distinguishing the different regimes. Shown below is the basic model setup (based on a dual-regime TDPM for elaboration):
|
RSTi,j=Ci+(p1∑j=1β1jRSTi,t−j+p2∑j=1η1jPIi,t−j+p3∑J=1φ1jRGYi,t−j)I(qi,t−d≤γ)+(p1∑j=1β2jRSTi,t−j+p2∑j=1η2jPIi,t−j+p3∑j=1φ2jRGYi,t−j)I(qi,t−d>γ)+ei,t
|
(3)
|
where i =1~N,
t =1~T; RSTit is the dependent variable; PIit is the inflation variable that also includes expected and unexpected inflation; RGYi is another real independent variable; qi, t- is the threshold variable and real economic growth; and RGYit-d will be defined as the threshold variable in the present study with γ as the threshold value. I(RGYit−d≤γ) and I(RGYit−d>γ) are pointer variables that distinguish the regimes of low and high real economic growth, respectively; eit is the interference term; and β1j,β2j, η1j,η2j, and φ1j,φ2j are the estimated parameters of the dependent variable in each regime, respectively.
2.3. Research data
The present study includes the following samples: Taiwan, the G-7 nations, Europe, Asia, the US, the Middle East, Africa, and others totaling 38 countries. For more details, please refer to Appendix 2. In this study, multiple countries are employed as the primary subjects and the variables adopted are their stock indices, GDP, GDP deflator (or consumer price index, CPI), and others. These data are extracted from IMF's IFS database and AREMOS. The study period is from the first quarter of 1981 to the fourth quarter of 2014 totaling 34 years of quarterly data. The following is a brief introduction of the variables in the model:
(1) Real Stock Return (Rate) (RST): Stock price index listed on Dow Jones divided by GDP deflator (or CPI), then take the logarithm and perform differencing at the fourth lagged period to remove seasonality.7
7 As quarterly data are employed in this study, logarithm is performed; if differencing is performed only at the first lagged period, the rate of return generated may be subject to seasonality. Hence, this study performs differencing at the fourth lagged period Rt = lnXt-lnXt-4 to remove seasonality.
(2) Inflation (PI): Take logarithm of GDP deflator and perform differencing at the fourth lagged period. Based on the approach adopted in Katzur and Spierdijk (2013), employ AR (1) model setup to divide general inflation (PI) into expected inflation (PI_E) and unexpected inflation (PI_U).8
8 Based on the model setup of AR (1), the expected inflation in the present study can be regarded as inflation with adaptive expectations. See Appendix 3 for the estimate process.
(3) Real Economic Growth (Rate) (RGY): Adopt real GDP to represent RGY and derive the variable by dividing the GDP by the GDP deflator (or CPI), take a logarithm and perform differencing at the fourth lagged period.
In this study, two steps are involved in verifying the Fisher hypothesis and Fama's proxy hypothesis. Step (Ⅰ): Real stock return rate, general inflation, and expected or unexpected inflation are adopted to verify the Fisher hypothesis; when the inflation variables do not affect real stock return, the Fisher hypothesis is supported, but when the three inflation variables have significant negative impact on real stock return, then Fisher hypothesis is rejected, and hence step (Ⅱ) is followed to verify further if Fama's proxy hypothesis is supported. When real variables are incorporated into the model, and the significant impact that the three inflation variables originally have on real stock return disappears, then Fama's proxy hypothesis is supported; conversely, Fama's proxy hypothesis is rejected.
3. Empirical Result Analysis
Before estimating the model, it is necessary first to confirm whether the variables are stationary to avoid spurious regression. The following four panel data unit root tests are adopted in the present study: t-test in Levin et al. (2002), w-test in Im et al. (2003), and ADF–Fisher Chi-square test and PP-Fisher Chi-square test in Maddala and Wu (1999) to perform the unit root test on the variables. The results of the panel data unit root tests confirm that the three variables, RST, PI, and RGY are stationary; hence, subsequent model estimation can be performed.9
9 For the sake of brevity, the results of the panel data unit root tests are not presented in a table.
3.1. Linear model
This study firstly estimates the static linear model. The fourth lagged period is selected as the optimal based on the AIC principle and three groups of models are formed according to inflation. Model 1 corresponds to general inflation (PI), Model 2 corresponds to expected inflation (PI_E), and Model 3 corresponds to unexpected inflation (PI_U). In addition, two sub-models are formed in each model: Model A is to test step (Ⅰ): validation of Fisher hypothesis, that is, to test the impact of inflation on real stock return. Model B is to test step (Ⅱ) by incorporating the real variable (RGY) to verify if Fama's proxy hypothesis is supported. Table 1 shows the estimation results of the static linear model with Model 1A, Model 2A, and Model 3A, respectively, representing general inflation, expected inflation, and unexpected inflation. Model 1B, Model 2B, and Model 3B, on the other hand, represent the estimation models in step (Ⅱ).
Table 1. The empirical results of static linear model.
| Model No. |
Model 1A |
Model 1B |
|
Model 2A |
Model 2B |
|
Model 3A |
Model 3B |
| Dependent variable |
RST |
RST |
|
RST |
RST |
|
RST |
RST |
| Inflation variable |
PI |
PI |
|
PI_E |
PI_E |
|
PI_U |
PI_U |
| constant |
0.069 |
0.036 |
|
0.061 |
0.031 |
|
0.043 |
0.018 |
|
(0.000) |
(0.000) |
|
(0.000) |
(0.000) |
|
(0.000) |
(0.001) |
| η1 |
-1.384 |
-0.622 |
|
-1.551 |
-0.805 |
|
-1.289 |
-0.602 |
|
(0.000) |
(0.004) |
|
(0.000) |
(0.001) |
|
(0.000) |
(0.004) |
| η2 |
0.110 |
-0.042 |
|
0.217 |
-0.079 |
|
-0.999 |
-0.541 |
|
(0.741) |
(0.899) |
|
(0.550) |
(0.824) |
|
(0.000) |
(0.014) |
| η3 |
-0.076 |
-0.203 |
|
0.674 |
0.641 |
|
-1.001 |
-0.706 |
|
(0.821) |
(0.540) |
|
(0.063) |
(0.066) |
|
(0.000) |
(0.001) |
| η4 |
0.742 |
0.559 |
|
0.216 |
0.003 |
|
-0.574 |
-0.172 |
|
(0.001) |
(0.010) |
|
(0.358) |
(0.989) |
|
(0.008) |
(0.411) |
| ∑4j=1ηj |
-0.609 |
-0.307 |
|
-0.444 |
-0.240 |
|
-3.864 |
-2.020 |
| χ24 |
45.832 |
9.987 |
|
21.011 |
5.368 |
|
129.074 |
35.741 |
|
(0.000) |
(0.002) |
|
(0.000) |
(0.021) |
|
(0.000) |
(0.000) |
| ϕ1 |
|
2.479 |
|
|
2.672 |
|
|
2.578 |
|
|
(0.000) |
|
|
(0.000) |
|
|
(0.000) |
| ϕ2 |
|
-0.442 |
|
|
-0.640 |
|
|
-0.499 |
|
|
(0.042) |
|
|
(0.003) |
|
|
(0.022) |
| ϕ3 |
|
-0.871 (0.000) |
|
|
-0.845 (0.000) |
|
|
-0.859 (0.000) |
| ϕ4 |
|
-0.540 |
|
|
-0.502 |
|
|
-0.465 |
|
|
(0.001) |
|
|
(0.002) |
|
|
(0.004) |
Notes: χ24 (tested statistic) for test H0:∑ηj=0,j=1,2,3,4, equal to investigate whether the effect of the inflation to the RST, significance or not.
The PI, PI_E, PI_U are inflation, expected inflation and unexpected inflation respectively.
The models show below:
Model 1A: RSTi,j=Ci+4∑j=1ηjPIi,t−j+ei,t Model 1B: RSTi,j=Ci+4∑j=1ηjPIi,t−j+4∑j=1φjRGYi,t−j+εi,t
Model 2A: RSTi,j=Ci+4∑j=1ηjPI_Ei,t−j+ei,t Model 2B: RSTi,j=Ci+4∑j=1ηjPI_Ei,t−j+4∑j=1φjRGYi,t−j+εi,t
Model 3A:RSTi,j=Ci+4∑j=1ηjPI_Ui,t−j+ei,t Model 3B: RSTi,j=Ci+4∑j=1ηjPI_Ui,t−j+4∑j=1φjRGYi,t−j+εi,t |
According to the coefficients of Model 1A, Model 2A, Model 3A, and the results of the joint tests, (∑4j=1ηj), general inflation, expected inflation, and unexpected inflation show the significantly negative impact on real stock return indicating that all the three models violate the Fisher hypothesis. As seen from the estimation results in Model 1B, Model 2B, and Model 3B, although real economic growth has a significant impact on real stock return, the impact of the three different types of inflation on real stock return remains to be significantly negative. The overall empirical results of the static linear model show that the Fisher hypothesis and Fama's proxy hypothesis are not supported. As the nonlinear relationships among variables are not considered in the setup of the static linear model, and the dynamic effects are ignored, these may likely be the impact factors for the establishment of the Fisher hypothesis and Fama's proxy hypothesis. Thus, this study will further analyze the empirical results in a nonlinear model.
3.2. Nonlinear model
In this study, a TDPM is constructed, and real economic growth is employed as the threshold variable with the following economic implications: different economic growth in different regimes will affect the relationship between inflation and real stock return within that regime, which will also affect whether the Fisher hypothesis and Fama's proxy hypothesis are supported. For example, the threshold value is the critical value that distinguishes the different real economic growth and is sufficient to cause changes in the relationship between inflation and stock return. If the threshold effect is significant, it means that the empirical model is fit for use in a nonlinear framework. In addition, to lower possible bias in a static model, dynamic setup is adopted in the model, that is, a lagged dependent variable for real stock return is added as an independent variable.10
10 A lagged dependent variable of real stock return is added as an independent variable in a nonlinear model to construct a dynamic panel data model. This study will decide whether the first or the fourth lagged variable is a better selection to be included in the empirical model.
Before constructing a nonlinear model, the existence of nonlinear relationship (that is, threshold effect) among variables should be tested in the empirical process. Thus, the test for linearity is first performed to confirm if the threshold model is fit for collecting sample data for threshold estimation. To differentiate from the linear static model, three different groups of nonlinear sub-models are labeled as "C" and "D" that also adopt the dynamic model settings. Among them, in addition to the three types of inflation variables that are originally employed as independent variables, a lagged dependent variable of real stock return is added as an independent variable in sub-model C to test if the Fisher hypothesis is supported. Then, in sub-model D, lagged variables of real economic growth from the first to fourth periods will be added as independent variables to test if Fama's hypothesis is supported.
In addition, to explore whether characteristics of the different country cluster will influence the establishment of Fisher hypothesis and Fama's proxy hypothesis, the sample regions of the present study are classified into two groups. The first group is the OECD member countries (countries that became members since 1993) totaling 19 called the OECD19. The second group of countries (or regions) is those with less uniform background totaling 19 countries (or regions) and is regarded as mixed19.
Table 2 lists the results of linearity testing (full sample). A total of six models are formed to perform linearity testing: Model 1C, 2C, and 3C, and Model 1D, 2D, and 3D. This study adopts Model 1C, 2C, and 3C as the basis to investigate whether the Fisher hypothesis is supported; delayed real economic growth is employed as the threshold variable. According to the test results in Table 3, when the real economic growth of the four-lag periods is set as the threshold variables respectively, the test statistic is the greatest when the real economic growth of the third lagged period is set as the threshold variable. Thus, the optimal threshold of the present study is -0.0090. The estimated coefficient of the lagged dependent variable is adjusted in the present study based on the model adopted in Chen and Lin (2010). Bootstrapping is then employed to find the critical value of the estimated coefficients to test for significance in the coefficients of independent variables in each regime and the overall effect of the general inflation (expected and unexpected).
Table 2. The results of Linear testing.
| Null Hypothesis |
Threshold variable |
Threshold value |
Tested statistic |
P-value |
| Model 1C |
|
|
|
|
| one regime |
RGYit-1 |
-0.0084 |
159.565 |
(0.000) |
| one regime |
RGYit-2 |
-0.0088 |
150.499 |
(0.003) |
| one regime |
RGYit-3 |
-0.0090 |
168.753 |
(0.003) |
| one regime |
RGYit-4 |
-0.0048 |
126.057 |
(0.015) |
| two regime |
RGYit-3 |
-0.0090, 0.0349 |
86.849 |
(0.178) |
|
|
|
|
|
| Model 2C |
|
|
|
|
| one regime |
RGYit-1 |
-0.0084 |
104.916 |
(0.000) |
| one regime |
RGYit-2 |
-0.0088 |
149.439 |
(0.005) |
| one regime |
RGYit-3 |
-0.0090 |
151.249 |
(0.005) |
| one regime |
RGYit-4 |
-0.0048 |
115.025 |
(0.038) |
| two regime |
RGYit-3 |
-0.0090, 0.0349 |
83.671 |
(0.190) |
|
|
|
|
|
| Model 3C |
|
|
|
|
| one regime |
RGYit-1 |
-0.0084 |
145.177 |
(0.005) |
| one regime |
RGYit-2 |
-0.0042 |
150.940 |
(0.000) |
| one regime |
RGYit-3 |
-0.0090 |
168.655 |
(0.000) |
| one regime |
RGYit-4 |
-0.0048 |
131.464 |
(0.010) |
| two regime |
RGYit-3 |
-0.0090, 0.0349 |
87.163 |
(0.145) |
|
|
|
|
|
| Model 1D |
|
|
|
|
| one regime |
RGYit-3 |
-0.0090 |
134.336 |
(0.033) |
| two regime |
RGYit-3 |
-0.0090, 0.0349 |
97.309 |
(0.118) |
|
|
|
|
|
| Model 2D |
|
|
|
|
| one regime |
RGYit-3 |
-0.0090 |
154.322 |
(0.010) |
| two regime |
RGYit-3 |
-0.0090, 0.0349 |
96.919 |
(0.125) |
|
|
|
|
|
| Model 3D |
|
|
|
|
| one regime |
RGYit-3 |
-0.0090 |
170.877 |
(0.000) |
| two regime |
RGYit-3 |
-0.0090, 0.0349 |
96.834 |
(0.090) |
|
|
|
|
|
| Model 1M |
|
|
|
|
| one regime |
RGYit-3 |
-0.0090 |
170.682 |
(0.003) |
| two regime |
RGYit-3 |
-0.0041, 0.0349 |
103.042 |
(0.110) |
|
|
|
|
|
| Model 2M |
|
|
|
|
| one regime |
RGYit-3 |
-0.0090 |
151.842 |
(0.005) |
| two regime |
RGYit-3 |
-0.0090, 0.0349 |
96.695 |
(0.153) |
|
|
|
|
|
| Model 3M |
|
|
|
|
| one regime |
RGYit-3 |
-0.0090 |
162.002 |
(0.001) |
| two regime |
RGYit-3 |
-0.0090, 0.0349 |
97.166 |
(0.135) |
| Note: the threshold variable is real GDP growth rate (RGY). |
Table 3. The empirical results of TDPM (full sample).
| Model No. |
Model 1C |
|
|
|
Model 1D |
|
|
|
|
Adj. coef |
p-value |
CV. 95% |
CV. 5% |
Adj. coef |
p-value |
CV. 95% |
CV. 5% |
| RGYi,t−3≤−0.0090 |
|
|
|
|
|
|
|
|
| β11 |
0.905 |
(0.000) |
0.050 |
-0.061 |
1.015 |
(0.000) |
0.053 |
-0.071 |
| β14 |
-0.244 |
(0.000) |
0.053 |
-0.034 |
-0.328 |
(0.000) |
0.047 |
-0.045 |
| η11 |
-1.292 |
(0.000) |
0.614 |
-0.813 |
-1.194 |
(0.006) |
0.746 |
-0.733 |
| η12 |
0.910 |
(0.768) |
1.268 |
-1.057 |
0.934 |
(0.198) |
1.194 |
-1.183 |
| η13 |
-0.018 |
(0.536) |
1.043 |
-1.224 |
-0.345 |
(0.662) |
1.236 |
-1.181 |
| η14 |
-0.018 |
(0.523) |
0.647 |
-0.654 |
0.524 |
(0.238) |
0.688 |
-0.833 |
| ∑4j=1η1j |
-0.418 |
(0.000) |
0.144 |
-0.274 |
-0.080 |
(0.336) |
0.294 |
-0.317 |
| ϕ11 |
|
|
|
|
-0.005 |
(0.501) |
0.530 |
-0.533 |
| ϕ12 |
|
|
|
|
-0.097 |
(0.465) |
0.661 |
-0.770 |
| ϕ13 |
|
|
|
|
0.087 |
(0.487) |
0.912 |
-0.634 |
| ϕ14 |
|
|
|
|
0.711 |
(0.006) |
0.424 |
-0.657 |
| RGYi,t−3>−0.0090 |
|
|
|
|
|
|
|
|
| β21 |
1.233 |
(0.000) |
0.015 |
-0.047 |
1.274 |
(0.000) |
0.024 |
-0.048 |
| β24 |
-0.339 |
(0.000) |
0.016 |
-0.047 |
-0.338 |
(0.000) |
0.021 |
-0.047 |
| η21 |
-0.480 |
(0.034) |
0.258 |
-0.379 |
-0.381 |
(0.096) |
0.396 |
-0.466 |
| η22 |
0.258 |
(0.612) |
0.461 |
-0.497 |
0.139 |
(0.622) |
0.636 |
-0.611 |
| η23 |
0.195 |
(0.470) |
0.507 |
-0.555 |
0.176 |
(0.673) |
0.593 |
-0.560 |
| η24 |
-0.141 |
(0.390) |
0.258 |
-0.446 |
-0.065 |
(0.442) |
0.420 |
-0.437 |
| ∑4j=1η2j |
-0.168 |
(0.525) |
0.020 |
-0.278 |
-0.133 |
(0.227) |
0.150 |
-0.233 |
| ϕ21 |
|
|
|
|
0.245 |
(0.050) |
0.288 |
-0.296 |
| ϕ22 |
|
|
|
|
-0.311 |
(0.118) |
0.446 |
-0.348 |
| ϕ23 |
|
|
|
|
0.010 |
(0.462) |
0.337 |
-0.336 |
| ϕ24 |
|
|
|
|
0.219 |
(0.084) |
0.297 |
-0.274 |
Note: Using the method of bootstrapping to get the critical value (CV).
Testing the hypothesis H0:∑ηj=0,j=1,2,3,4, equal to investigate whether the effect of the inflation to the RST, significance or not. The models show below:
Model 1C:RSTi,j=Ci+(∑j=1,4β1jRSTi,t−j+4∑j=1η1jPIi,t−j)I(RGYi,t−3≤−0.0090)
+(∑j=1,4β2jRSTi,t−j+4∑j=1η2jPIi,t−j)I(RGYi,t−3>−0.0090)+ei,t
Model 1D:RSTi,j=Ci+(∑j=1,4β1jRSTi,t−j+4∑j=1η1jPIi,t−j+4∑J=1φ1jRGYi,t−j)I(RGYi,t−3≤−0.0090)
+(∑j=1,4β2jRSTi,t−j+4∑j=1η2jPIi,t−j+4∑j=1φ2jRGYi,t−j)I(RGYi,t−3>−0.0090)+ei,t |
Tables 3, 4, and 5 list the estimation results of the six TDPMs, namely Model 1C, 1D, 2C, 2D, 3C, and 3D, respectively. As shown in the estimation results, the real stock return of the first and fourth lagged periods have a significant impact on the current real stock return indicating that the empirical model should have dynamic adjustment settings. According to the empirical results of Model 1C in Table 3, the overall effect of general inflation of all four lagged periods (first to fourth) is significantly negative on stock return in regime with low real economic growth (RGYit−3≤−0.0090), hereinafter referred to as Regime 1, indicating that the Fisher hypothesis is rejected in Regime 1. In a regime with high real economic growth, from now on referred as Regime 2, the overall effect of the general inflation of all four lagged periods (first to fourth) is insignificantly negative on stock return, indicating that the Fisher hypothesis is supported in Regime 2. As shown in the estimation results of Model 1D in Table 4, after real variables are incorporated into the model, although the overall effect of general inflation on the real stock return is still negative, it is no longer significant in Regime 1, confirming that Fama's proxy hypothesis is supported in Regime 1.
Table 4. The empirical results of TDPM (full sample).
| Model No. |
Model 2C |
|
|
|
Model 2D |
|
|
|
|
Adj. coef |
p-value |
CV. 95% |
CV. 5% |
Adj. coef |
p-value |
CV. 95% |
CV. 5% |
| RGYi,t−3≤−0.0090 |
|
|
|
|
|
|
|
|
| β11 |
0.915 |
(0.000) |
0.059 |
-0.061 |
0.998 |
(0.000) |
0.053 |
-0.064 |
| β14 |
-0.255 |
(0.000) |
0.052 |
-0.032 |
-0.314 |
(0.000) |
0.053 |
-0.043 |
| η11 |
-1.039 |
(0.038) |
0.753 |
-0.769 |
-0.841 |
(0.116) |
0.850 |
-0.867 |
| η12 |
0.406 |
(0.562) |
1.229 |
-1.265 |
0.120 |
(0.559) |
1.387 |
-1.225 |
| η13 |
0.988 |
(0.172) |
1.205 |
-1.153 |
1.186 |
(0.114) |
1.240 |
-1.352 |
| η14 |
-0.780 |
(0.035) |
0.620 |
-0.727 |
-0.547 |
(0.118) |
0.749 |
-0.783 |
| ∑4j=1η1j |
-0.426 |
(0.002) |
0.048 |
-0.263 |
-0.081 |
(0.379) |
0.314 |
-0.340 |
| ϕ11 |
|
|
|
|
0.295 |
(0.302) |
0.504 |
-0.526 |
| ϕ12 |
|
|
|
|
-0.417 |
(0.358) |
0.660 |
-0.724 |
| ϕ13 |
|
|
|
|
0.071 |
(0.439) |
0.870 |
-0.626 |
| ϕ14 |
|
|
|
|
0.697 |
(0.010) |
0.444 |
-0.690 |
|
|
|
|
|
|
|
|
|
| RGYi,t−3>−0.0090 |
|
|
|
|
|
|
|
|
| β21 |
1.241 |
(0.000) |
0.016 |
-0.047 |
1.273 |
(0.000) |
0.019 |
-0.044 |
| β24 |
-0.340 |
(0.000) |
0.014 |
-0.046 |
-0.340 |
(0.000) |
0.020 |
-0.041 |
| η21 |
-0.308 |
(0.366) |
0.296 |
-0.448 |
-0.326 |
(0.214) |
0.379 |
-0.444 |
| η22 |
0.225 |
(0.518) |
0.530 |
-0.546 |
0.187 |
(0.634) |
0.589 |
-0.561 |
| η23 |
0.306 |
(0.364) |
0.544 |
-0.506 |
0.393 |
(0.220) |
0.538 |
-0.613 |
| η24 |
-0.357 |
(0.218) |
0.293 |
-0.442 |
-0.367 |
(0.118) |
0.390 |
-0.370 |
| ∑4j=1η2j |
-0.134 |
(0.565) |
0.048 |
-0.344 |
-0.113 |
(0.247) |
0.168 |
-0.229 |
| ϕ21 |
|
|
|
|
0.364 |
(0.008) |
0.213 |
-0.253 |
| ϕ22 |
|
|
|
|
-0.417 |
(0.030) |
0.309 |
-0.310 |
| ϕ23 |
|
|
|
|
0.025 |
(0.508) |
0.347 |
-0.307 |
| ϕ24 |
|
|
|
|
0.243 |
(0.062) |
0.206 |
-0.272 |
Note: Using the method of bootstrapping to get the critical value (CV).
Testing the hypothesis H0:∑ηj=0,j=1,2,3,4 equal to investigate whether the effect of the inflation to the RST, significance or insignificance. The models show below:
Model 2C:RSTi,j=Ci+(∑j=1,4β1jRSTi,t−j+4∑j=1η1jPI_Ei,t−j)I(RGYi,t−3≤−0.0090)
+(∑j=1,4β2jRSTi,t−j+4∑j=1η2jPI_Ei,t−j)I(RGYi,t−3>−0.0090)+ei,t
Model 2D:RSTi,j=Ci+(∑j=1,4β1jRSTi,t−j+4∑j=1η1jPI_Ei,t−j+4∑J=1φ1jRGYi,t−j)I(RGYi,t−2≤−0.0041)
+(∑j=1,4β2jRSTi,t−j+4∑j=1η2jPI_Ei,t−j+4∑j=1φ2jRGYi,t−j)I(RGYi,t−2>−0.0041)+ei,t |
Table 5. The empirical results of TDPM (full sample).
| Model No. |
Model 3C |
|
|
|
Model 3D |
|
|
|
|
Adj. coef |
p-value |
CV. 95% |
CV. 5% |
Adj. coef |
p-value |
CV. 95% |
CV. 5% |
| RGYi,t−3≤−0.0090 |
|
|
|
|
|
|
|
|
| β11 |
0.906 |
(0.000) |
0.058 |
-0.062 |
0.989 |
(0.000) |
0.052 |
-0.067 |
| β14 |
-0.203 |
(0.000) |
0.053 |
-0.031 |
-0.327 |
(0.000) |
0.047 |
-0.049 |
| η11 |
-0.985 |
(0.024) |
0.691 |
-0.663 |
-1.083 |
(0.018) |
0.712 |
-0.710 |
| η12 |
-0.188 |
(0.542) |
0.865 |
-0.635 |
-0.242 |
(0.628) |
0.760 |
-0.789 |
| η13 |
-0.386 |
(0.462) |
0.678 |
-0.836 |
-0.557 |
(0.232) |
0.823 |
-0.778 |
| η14 |
0.049 |
(0.571) |
0.688 |
-0.659 |
0.298 |
(0.496) |
0.741 |
-0.712 |
| ∑4j=1η1j |
-1.510 |
(0.015) |
-0.963 |
-1.295 |
-1.584 |
(0.013) |
1.092 |
-1.109 |
| ϕ11 |
|
|
|
|
0.102 |
(0.651) |
0.475 |
-0.558 |
| ϕ12 |
|
|
|
|
-0.164 |
(0.742) |
0.640 |
-0.723 |
| ϕ13 |
|
|
|
|
0.005 |
(0.648) |
0.815 |
-0.519 |
| ϕ14 |
|
|
|
|
0.748 |
(0.008) |
0.414 |
-0.632 |
|
|
|
|
|
|
|
|
|
| RGYi,t−3>−0.0090 |
|
|
|
|
|
|
|
|
| β21 |
1.234 |
(0.000) |
0.018 |
-0.048 |
1.273 |
(0.000) |
0.021 |
-0.042 |
| β24 |
-0.333 |
(0.000) |
0.018 |
-0.044 |
-0.336 |
(0.000) |
0.020 |
-0.039 |
| η21 |
-0.471 |
(0.032) |
0.357 |
-0.344 |
-0.395 |
(0.064) |
0.379 |
-0.342 |
| η22 |
-0.154 |
(0.466) |
0.345 |
-0.352 |
-0.206 |
(0.312) |
0.362 |
-0.342 |
| η23 |
0.005 |
(0.505) |
0.317 |
-0.323 |
-0.054 |
(0.786) |
0.362 |
-0.360 |
| η24 |
0.229 |
(0.316) |
0.329 |
-0.361 |
0.264 |
(0.268) |
0.379 |
-0.384 |
| RGYi,t−3>−0.0090 |
-0.391 |
(0.133) |
-0.592 |
-0.730 |
-0.390 |
(0.132) |
0.700 |
-0.599 |
| ϕ21 |
|
|
|
|
0.288 |
(0.050) |
0.237 |
-0.239 |
| ϕ22 |
|
|
|
|
-0.326 |
(0.091) |
0.305 |
-0.319 |
| ϕ23 |
|
|
|
|
0.014 |
(0.918) |
0.364 |
-0.295 |
| ϕ24 |
|
|
|
|
0.242 |
(0.072) |
0.215 |
-0.264 |
Note: Using the method of bootstrapping to get the critical value (CV).
Testing the hypothesis H0:∑ηj=0,j=1,2,3,4, equal to investigate whether the effect of the inflation to the RST, significance or insignificance. The models show below:
Model 3C:RSTi,j=Ci+(∑j=1,4β1jRSTi,t−j+4∑j=1η1jPI_Ui,t−j)I(RGYi,t−2≤−0.0041)
+(∑j=1,4β2jRSTi,t−j+4∑j=1η2jPI_Ui,t−j)I(RGYi,t−3>−0.0090)+ei,t
Model 3D:RSTi,j=Ci+(∑j=1,4β1jRSTi,t−j+4∑j=1η1jPI_Ui,t−j+4∑J=1φ1jRGYi,t−j)I(qi,t−3≤−0.0090)
+(∑j=1,4β2jRSTi,t−j+4∑j=1η2jPI_Ui,t−j+4∑j=1φ2jRGYi,t−j)I(qi,t−3>−0.0090)+ei,t |
As the results of Model 2C in Table 4 show, expected inflation has a negative impact on real stock return (Regime 1: -0.391, Regime 2:
-0.134) that is significant in Regime 1 and insignificant in Regime 2, indicating that the Fisher hypothesis is not supported in Regime 1 but supported in Regime 2. The results of Model 2D show that the overall effect of expected inflation on real stock return in both Regime 1 and Regime 2 are insignificantly negative, indicating that after the variable of real economic growth is added, the significantly negative impact that expected inflation originally has on real stock return in Model 2C of Regime 1 is only spurious. Such a result indicates that in Regime 1 when inflation is expected, Fama's proxy hypothesis is supported.
As shown in Table 5, although the Fisher hypothesis is supported in the three models of Regime 2, Fama's proxy hypothesis is not supported in Model 3D of Regime 1, which is different from the result in Model 1D and Model 2D of Regime 1. The results in Model 3D are significantly different than in Model 1D and Model 2D implying that expected inflation and unexpected inflation play a unique role in the establishment of Fama's proxy hypothesis. Different characteristics of these two types of inflation lead to two contrary conclusions of whether Fama's proxy hypothesis is supported. As unexpected inflation is derived from the residual of the inflation equation, AR (1), it is speculated that the residual may possess a high degree of inherent uncertainty making the impact of unexpected inflation significantly negative on real stock return even after other real variables are added to the model.
To summarize the estimation results in Tables 3 to 5, the Fisher hypothesis is supported in Regime 2 (high real economic growth) and Fama's proxy hypothesis is supported in Regime 1 (low real economic growth) when general or expected inflation is adopted, which is consistent with the multiple arguments presented in Kim and In (2005), Kim and Tyoo (2011), and Tsong and Lee (2013). However, the conclusions of the present study are more comprehensive than these three studies, which is the key contribution of this study. In addition, a dynamic model setup is confirmed necessary, indicating that important variables are missing in previous static model setup. Empirical results that both support and reject Fama's proxy hypothesis are often found in previous studies. As shown in the empirical results of the present study, the contrary conclusions may be due to factors such as the different characteristics of inflation variables being adopted, dynamic vs. static model setup, and linear vs. nonlinear model framework.
Thirty-eight countries are selected as the research subjects of the present study. Among them, 23 are OECD member countries. To further understand whether different country clusters will interfere the establishment of the Fisher hypothesis and Fama's proxy hypothesis, the present study divides the 38 countries into two sub-sample groups, namely, the OECD group of OECD member countries that have uniform characteristics and the mixed group of countries of less uniform characteristics. There are 19 countries (or regions) in each sample group. Please see Appendix 2 for a detailed list of countries.
Table 6 lists the results of linearity testing (two sub-samples), six model combinations are formed in each sub-sample to perform linearity testing (based on the model settings in Models 1C, 2C, 3C, 1D, 2D, and 3D). As shown in Table 7, threshold effect exists in all the models of both sub-samples; the optimal model setting is the dual regime with same settings as in full sample except that there are significant differences in setting the number of lagged periods for the threshold variable and the threshold value. For example, the threshold variable is set at the first lagged period for the OECD19 countries in the TDPM, whereas the threshold variable is set at the second lagged period in the TDPM for the mixed group. Regarding the threshold value, it varies among the OECD19 countries in the TDPM at 0.0375, 0.0097, and -0.0058, whereas the threshold value remains the same in the TDPM among the mixed19 countries with the optimal threshold mean of -0.0130.
Table 6. The results of linear testing (two sub-samples).
| Null hypothesis |
Threshold variable |
Threshold value |
Tested statistic |
P-value |
| OECD19 countries |
|
|
|
|
| Model 1C* one regime |
RGYit-1 |
0.0097 |
82.025 |
(0.005) |
| two regime |
RGYit-1 |
0.0097, 0.0375 |
43.724 |
(0.645) |
| Model 2C* one regime |
RGYit-1 |
-0.0058 |
74.929 |
(0.027) |
| two regime |
RGYit-1 |
-0.0058, 0.0375 |
61.505 |
(0.290) |
| Model 3C* one regime |
RGYit-1 |
0.0375 |
79.247 |
(0.015) |
| two regime |
RGYit-3 |
0.0059, 0.0375 |
60.008 |
(0.194) |
| Model 1D* one regime |
RGYit-1 |
0.0375 |
94.313 |
(0.032) |
| two regime |
RGYit-1 |
0.0066, 0.0375 |
71.163 |
(0.120) |
| Model 2D* one regime |
RGYit-1 |
0.0375 |
92.997 |
(0.041) |
| two regime |
RGYit-1 |
-0.0040, 0.0375 |
71.223 |
(0.118) |
| Model 3D* one regime |
RGYit-1 |
0.0375 |
95.115 |
(0.031) |
| two regime |
RGYit-1 |
0.0130, 0.0375 |
69.889 |
(0.193) |
| Mixed 19countries |
|
|
|
|
| Model 1C** one regime |
RGYit-2 |
-0.0130 |
97.819 |
(0.000) |
| two regime |
RGYit-2 |
-0.0130, 0.0715 |
46.945 |
(0.420) |
| Model 2C** one regime |
RGYit-2 |
-0.0130 |
95.256 |
(0.000) |
| two regime |
RGYit-2 |
-0.0130, 0.0715 |
41.819 |
(0.508) |
| Model 3C** one regime |
RGYit-2 |
-0.0130 |
90.282 |
(0.003) |
| two regime |
RGYit-2 |
-0.0130, 0.0715 |
43.682 |
(0.477) |
| Model 1D** one regime |
RGYit-2 |
-0.0130 |
112.802 |
(0.000) |
| two regime |
RGYit-2 |
-0.0130, 0.0715 |
52.647 |
(0.368) |
| Model 2D** one regime |
RGYit-2 |
-0.0130 |
114.158 |
(0.000) |
| two regime |
RGYit-2 |
-0.0130, 0.0715 |
46.293 |
(0.550) |
| Model 3D** one regime |
RGYit-2 |
0.0375 |
95.115 |
(0.031) |
| two regime |
RGYit-2 |
0.0130, 0.0375 |
69.889 |
(0.193) |
| Note: the threshold variable is real GDP growth rate (RGY). |
Table 7. The empirical results of the OECD 19 countries.
| Model No. |
Model 1C* |
|
|
|
Model 1D* |
|
|
|
|
Adj. coef |
p-value |
CV. 95% |
CV. 5% |
Adj. coef |
p-value |
CV. 95% |
CV. 5% |
| RGYi,t−2≤0.0097 |
|
|
|
|
|
|
|
|
| ∑4j=1η1j |
-0.200 |
(0.000) |
-0.693 |
-1.586 |
-0.049 |
(0.336) |
0.082 |
-0.519 |
| RGYi,t−2>0.0097 |
|
|
|
|
|
|
|
|
| ∑4j=1η2j |
0.126 |
(0.154) |
0.152 |
-0.377 |
0.056 |
(0.252) |
1.152 |
-0.573 |
|
|
|
|
|
|
|
|
|
| Model No. |
Model 2C* |
|
|
|
Model 2D* |
|
|
|
| RGYi,t−1≤−0.0058 |
|
|
|
|
|
|
|
|
| ∑4j=1η1j |
-0.402 |
(0.016) |
-0.731 |
-2.141 |
-0.053 |
(0.236) |
0.031 |
-0.625 |
| RGYi,t−1>−0.0058 |
|
|
|
|
|
|
|
|
| ∑4j=1η2j |
0.047 |
(0.500) |
0.209 |
-0.376 |
-0.043 |
(0.464) |
0.232 |
-0.676 |
|
|
|
|
|
|
|
|
|
| Model No. |
Model 3C* |
|
|
|
Model 3D* |
|
|
|
| RGYi,t−3≤0.0375 |
|
|
|
|
|
|
|
|
| ∑4j=1η1j |
-2.635 |
(0.000) |
-0.963 |
-1.236 |
-0.996 |
(0.050) |
1.210 |
-0.788 |
| RGYi,t−3>0.0375 |
|
|
|
|
|
|
|
|
| ∑4j=1η2j |
0.464 |
(0.390) |
0.885 |
-0.882 |
-0.348 |
(0.467) |
1.115 |
-1.633 |
| Notes: Using the method of bootstrapping to get the critical value (CV). |
To alleviate confusion to readers, the estimation results of the TDPM in both sub-samples are presented in a summary format. Table 7 is a summary of the estimation results of the six TDPMs in the OECD19 group as denoted by "*". Table 8 is a summary of the estimation results in the six TDPMs in the mixed19 as denoted by "**". The result summaries shown in Tables 7 and 8 reveal that the Fisher hypothesis is supported in Regime 2 generating consistent results across all 12 models that are also consistent with the empirical results in full sample, clearly showing that the argument is robust. However, when the threshold variable is less than (or equal to) the threshold value, that is in Regime 1, the overall effect of inflation (expected and unexpected) has a significantly negative impact on stock return in the six models of 1C*, 2C*, 3C*, 1C**, 2C**, and 3C**. In other words, the Fisher hypothesis is not supported in Regime 1. Changes are observed after real economic growth variable is added to the test model. For example, in models 1D*, 2D*, and 2D** of Regime 1, the significant impact of general inflation and expected inflation on real stock return disappears, indicating that Fama's proxy hypothesis is supported in these three models of Regime 1. In Models 3D*, 1D**, and 3D** of Regime 1, the significant impact of general inflation and unexpected inflation on real stock return still exists. Hence, Fama's proxy hypothesis is not supported in these three models of Regime 1. As seen, differences exist between the two groups of countries. Regarding the OECD19 countries, for example, the data characteristic of general inflation tends to be more of expected nature, thereby supporting Fama's proxy hypothesis. Contrarily, regarding the mixed19 countries, the data characteristic of general inflation tends to be more of unexpected nature, thereby rejecting Fama's proxy hypothesis in Regime 1.
Table 8. The empirical results of the mixed 19 countries.
| Model No. |
Model 1C** |
|
|
Model 1D** |
|
|
| Adj. coef |
p-value |
CV. 95% |
CV. 5% |
Adj. coef |
p-value |
CV. 95% |
CV. 5% |
| RGYi,t−2≤−0.0130 |
|
|
|
|
|
|
|
|
| ∑4j=1η1j |
-0.667 |
(0.000) |
0.122 |
-0.273 |
-0.532 |
(0.026) |
0.386 |
-0.383 |
| RGYi,t−2>−0.0130 |
|
|
|
|
|
|
|
|
| ∑4j=1η2j |
-0.060 |
(0.556) |
0.150 |
-0.344 |
-0.012 |
(0.652) |
0.182 |
-0.297 |
|
|
|
|
|
|
|
|
|
| Model No. |
Model 2C** |
|
|
Model 2D** |
|
|
| RGYi,t−2≤−0.0130 |
|
|
|
|
|
|
|
|
| ∑4j=1η1j |
-0.620 |
(0.000) |
0.145 |
-0.263 |
-0.370 |
(0.136) |
0.393 |
-0.404 |
| RGYi,t−2>−0.0130 |
|
|
|
|
|
|
|
|
| ∑4j=1η2j |
-0.059 |
(0.527) |
0.156 |
-0.367 |
-0.115 |
(0.692) |
0.185 |
-0.323 |
|
|
|
|
|
|
|
| Model No. |
Model 3C** |
|
|
Model 3D** |
|
|
| RGYi,t−2≤−0.0130 |
|
|
|
|
|
|
|
|
| ∑4j=1η1j |
-1.619 |
(0.026) |
1.047 |
-1.387 |
-1.383 |
(0.048) |
1.270 |
-1.171 |
| RGYi,t−2>−0.0130 |
|
|
|
|
|
|
|
|
| ∑4j=1η2j |
-0.495 |
(0.362) |
0.799 |
-0.997 |
-0.489 |
(0.364) |
0.841 |
-1.171 |
Notes: Using the method of bootstrapping to get the critical value (CV).
Testing the hypothesis H0:∑ηj=0,j=1,2,3,4, equal to investigate whether the effect of the inflation to the RST, significance or insignificance. |
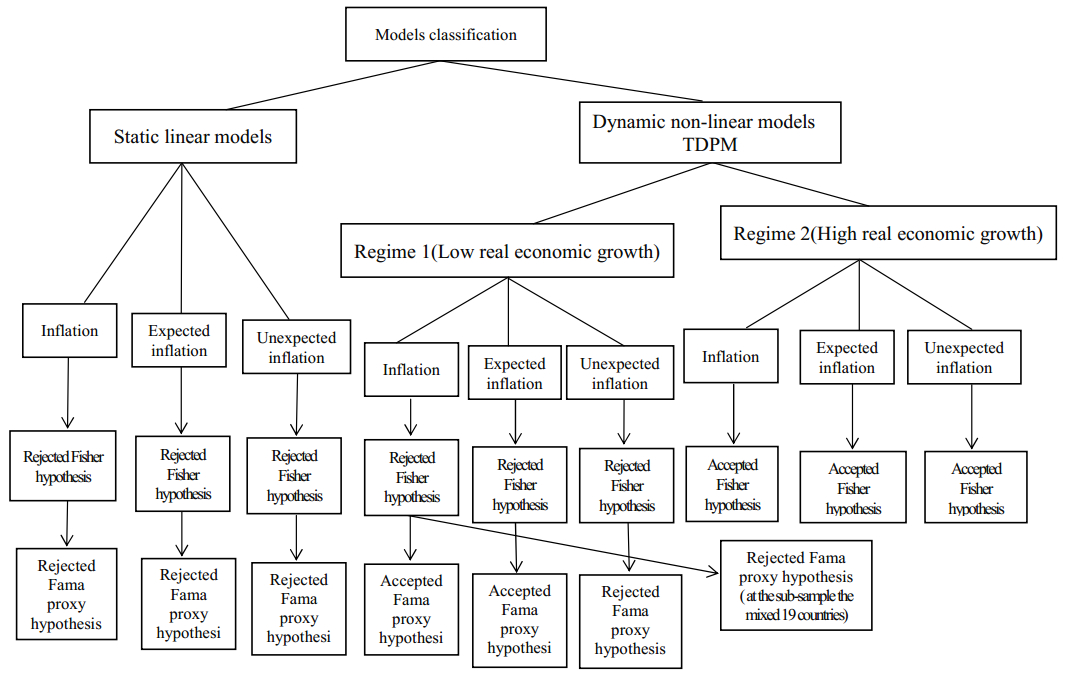
To summarize the results in Tables 7 and 8, besides the different settings in threshold variable and the threshold value, the conclusions in Model 1D and Model ID** of Regime 1 are contradictory. Their results are also inconsistent with the conclusion in full sample, especially the results in Regime 1. These inconsistent results indicate that when testing for support to the Fisher hypothesis and Fama's proxy hypothesis, the impact caused by the characteristics of different country groups should also be considered. To facilitate readers' ease of comparison, the results of the empirical models in the present study are presented in Figure 1 as follows.
Additionally, the empirical results point out that the Fisher hypothesis would be valid if the threshold variables is larger than threshold values. It means when nominal economic growth is larger than inflation, real stock returns would experience less negative impacts from inflation but larger positive effects from nominal economic growth. The results coincide with the Fisher hypothesis. In the lower (negative) real economic growth, the economic experienced higher inflation. The central bank would increase interest rate to suppress the inflation and then suppress stock market to downward. In the lower (negative) real economic growth, real stock returns are affected by larger inflation effects, but less economic growth effects. In this period, the Fisher hypothesis would not be validated. Why does the Fisher hypothesis get supported only at a certain growth rate? This is because the threshold variable is a critical and converted index which represents different real regimes and the variable is determined by erogeneity. The empirical results of this study show that the Fisher hypothesis would be valid in higher real economic growth studies if the threshold variable is larger than 0.0090, but would not be valid in lower real economic growth. To hedge inflation risks, investors and policy maker should select higher real economic growth regimes. In the lower real economic growth, they should consider whether they could sufficiently expect the inflation and could select OECD countries to implement hedging strategies in order to achieve best results.
4. Conclusion
This study adopts 34 years of quarterly panel data from 38 countries between 1981 and 2014 and bases on the TDPM put forward by Chen and Lin (2010) to investigate the correlations among real stock return, the three types of inflation, and real economic growth, and to test whether the Fisher hypothesis and Fama's proxy hypothesis are supported. This study employs linearity testing to confirm asymmetry in threshold effect, and the dual-regime TDPM is the optimal model framework. The empirical results show that different economic growth of a regime and its inflation play a role in whether Fama's hypothesis is supported. When real economic growth rate is greater than -0.0090 (Regime 2), the Fisher hypothesis is supported. When real economic growth rate is less than (or equal to) -.0090 (Regime 1), before the real variable is added, expected inflation and unexpected inflation have a significantly negative impact on real stock return and the Fisher hypothesis is not supported. After a real variable is added, the significantly negative impact of expected inflation on the real stock return that exists before the addition of real variable disappears, but the significant impact of unexpected inflation on real stock return remains. In order words, when real economic growth is negative, and inflation is expected, Fama's hypothesis will be supported.
The empirical results of the OECD19 and the mixed19 reveal that in testing whether the Fisher hypothesis and Fama's proxy hypothesis are supported, the empirical results in Regime 2 are similar to the conclusions in full sample, whereas the results of the two country groups are inconsistent with the results on full sample in Regime 1. The difference lies in the unique empirical results generated in Model 1D** of Regime 1 for the mixed19 countries, indicating that when conducting related research topic, the impact caused by different country characteristics should also be considered.
This study adopts a nonlinear TDPM and matches it with various inflation variables of different characteristics to obtain multiple arguments that support and reject the Fisher hypothesis and Fama's proxy hypothesis, which serve to explain why contradictory arguments are generated in past studies. The conclusions from the present study are robust and can provide a reference to investors in the financial market when making investment adjustment. After all, a comprehensive understanding of when the Fisher hypothesis and Fama's proxy hypothesis are supported is conducive in hedging inflation risks.
Conflict of Interest
All authors declare no conflicts of interest in this paper.
Appendix 1. The Institute: a Comparison of References
1. The recent literature on Fisher hypothesis.
| Author |
Empirical Period |
Country |
Main variables |
Econometric method |
Model specification |
Fisher hypothesis |
| Lee(2010) |
1927Q2~2007Q4, |
G7, Belgium, Netherland, Sweden and Switzerland |
Stock returns and inflation |
Structural VAR |
Linear model |
No |
| Francis and Tewari (2011) |
1998Q1~2007Q4 |
Ghana |
Stock return of Ghana Stock Exchange (GSE), CPI inflation |
Autoregressive distributed lag (ARDL) |
Linear model |
No |
| Kim and Ryoo(2011) |
1900M1~2009M6 |
United States |
Stock (price) return and (goods price) inflation rate |
The two regimes threshold vector error-correction model |
Non-Linear model |
Yes |
| Katzur and Spierdijk (2013) |
1985Q1~2011QQ1 |
United States |
Real stock returns, expected and unexpected inflation rates, and 5, 7, 10Y Treasure bill rate |
Bayesian approach and VAR model |
Linear model |
Yes |
| Tsong and Lee (2013) |
1957Q1~2010Q2 |
Australia, Belgium, Canada, Sweden, UK and USA. |
Nominal interest rates and inflation rate |
Quantile Cointegration methodology |
Non-Linear model |
No (at low Quantile) Yes (at high Quantile) |
| Everaert (2014) |
1983Q1~2010Q4 |
21 OECD countries |
Nominal interest rates and expected inflation rate |
Dynamic OLS, Full Modified OLS and Generalized Method of Moments |
Linear model |
Yes |
| Ozcan and Ari (2015) |
2000M1~2012M12 |
G7 |
Nominal interest rates and inflation rate |
panel unit-root and panel cointegration tests |
Linear model |
partial |
2. The literature on Fama proxy hypothesis.
| Author |
Empirical Period |
Country |
Main variables |
Econometric method |
Model specification |
Fama proxy hypothesis |
| Fama(1981) |
1953~ 1980 (Annual, Quarterly, and Monthly) |
United States |
Real stock returns, expected and unexpected inflation, the growth rate of industrial production and real GNP, and growth rate of the monetary base. |
The equation of real stock returns employed in the OLS estimates. |
Linear model |
Yes |
| Geske and Roll (1983) |
1947Q1~1980Q1 1968M8~1980M12 |
United States |
Stock Market return (based on S & P 500), the growth rate of unemployment, the growth rate in earnings, growth rate of (personal, corporate) taxes, and rate of U.S. Treasure debt. |
ARIMA model |
Linear model |
Yes |
| Cozier and Rahman (1988) |
1959Q1~1972Q4 1973Q1~1982Q4 |
Canada |
Real stock returns (Toronto Stock), actual inflation (base on CPI), expected inflation, unexpected inflation, growth rate of real GNP, and growth rate of money supply(M1) |
Autoregressive model, Causality test |
Linear model |
Yes |
| Lee(1992) |
1947M1 ~1987M12 |
United States |
Real stock returns, real interest rates, growth in industrial production, and rate of inflation |
VAR model |
Linear model |
Yes |
| Balduzzi (1995) |
1954Q1-1976Q4 1977Q1-1990Q4 |
United States |
Industrial-production growth, monetary-base growth, CPI inflation, 3-month TB rates, and returns on the equally-weighted NYSE portfolio |
VAR model and Vector moving averages model |
Linear model |
No |
| Caporal and Jung (1997) |
1947Q1~1991Q4 |
United States |
Growth rate of real GNP, growth rate of CPI, and growth rate of real New York stock exchange price index |
The system of equations, and using Full Information Maximum Likelihood. |
Linear model |
No |
| Gallagher and Taylor (2002) |
1957Q1~1997Q4 |
United States |
Real GDP, real stock price index, and consumer price index. |
Aggregate demand-aggregate supply (ADAS) model |
Linear model |
Yes |
| Kim (2003) |
1970Q1~1999Q4 |
Germany |
Returns of Stock index(DAX), inflation base on GDP deflator, and real (GDP) activity |
Asymmetric Granger-causality |
Non-Linear model |
Yes |
| Adrangi et al.(2005) |
1979M9~1998M12 |
United States |
Rate of inflation, unexpected rate of inflation, equity price index returns, and the growth in industrial production |
Uni-variable equation employed in the 2SLS estimates, and error correction model |
Linear model |
No |
| Omotor(2010) |
1985M1~2008M12,1985M2~1997M1,1997M1~2008M12 |
Nigeria |
Stock Price Index based on the Nigerian Exchange's All Share Index, CPI, Real activity(GDP) and money supply (M2) |
Johansen co-integration test and Granger causality tests |
Linear model |
Yes |
| Schmeling and Schrimpf (2011) |
1991M12~ 2007M9 |
France, Italy, Germany, Japan, UK., and the USA. |
expected CPI inflation, stock returns, the growth rate of money supply(M2), real output, and risk aversion |
Pooled model, VAR model, and in-sample and out-of-sample forecast |
Linear model |
No |
| Okuyan (2013) |
1987Q1-2012Q9 |
Turkey |
stock prices, consumption expenditures, industrial production index, employment level, and fixed investments |
ARDL bounds testing |
Linear model |
Yes |
Appendix 2.
Data summary
| National name |
Data period |
Stock market index |
Price variable |
|
(1981Q1~2014Q4) |
|
|
| Argentina |
1993Q1~ |
|
GDP deflator |
| Australia* |
|
|
GDP deflator |
| Austria* |
|
|
GDP deflator |
| Belgium* |
|
|
GDP deflator |
| Brazil |
1995Q1~ |
BOVESPA index |
GDP deflator |
| Canada* |
|
TSE 300 Composite index |
GDP deflator |
| China |
1992Q1~ |
Shanghai Composite index |
CPI |
| Chile# |
1997Q4~ |
IPSA index |
GDP deflator |
| Colombia |
1994Q1~ |
|
GDP deflator |
| Denmark* |
1989Q4~ |
|
GDP deflator |
| Finland* |
|
|
GDP deflator |
| France* |
|
|
GDP deflator |
| Germany* |
|
|
GDP deflator |
| Hong Kong |
|
Hang Seng index |
GDP deflator |
| India |
|
|
CPI |
| Indonesia |
1995Q3~ |
|
CPI |
| Ireland* |
1997Q1~ |
|
CPI |
| Israel# |
1987Q2~ |
TA100 index |
GDP deflator |
| Italy* |
|
|
GDP deflator |
| Japan* |
|
Nikkei 225 index |
GDP deflator |
| South Korea# |
|
SE Composite index |
GDP deflator |
| Malaysia |
1991q1~ |
KLSE Composite index |
GDP deflator |
| Mexico# |
1988Q1~ |
Share Index index(IPC) |
GDP deflator |
| Netherlands* |
|
|
GDP deflator |
| Norway* |
|
|
GDP deflator |
| New Zealand* |
1987Q2~ |
|
GDP deflator |
| Pakistan |
|
|
CPI |
| Philippines |
1989q2~ |
Manila Composite Index |
GDP deflator |
| Russian |
1995Q3~ |
Russian RTS Index |
GDP deflator |
| South Africa |
|
|
CPI |
| Singapore |
1982q1~ |
Straits Times Index |
CPI |
| Spain* |
|
|
GDP deflator |
| Sweden* |
|
|
GDP deflator |
| Switzerland* |
1988Q3~ |
Swiss Market Index (SMI) |
GDP deflator |
| Thailand |
1993Q1~ |
Bangkok SET Index |
GDP deflator |
| Taiwan, ROC. |
|
Weighted Stock Index(TAIEX) |
CPI |
| United Kingdom* |
1984Q1~ |
FTSE 100 Index |
GDP deflator |
| United States* |
|
|
|
Notes: If the column of data period is blank space, stand for this country have full-time data (1981q1~2014Q4), and the 19XXQX~ stand for this country the data begin timing.
If the column of stock market index is blank, stand for this country used the share price index of the IFS database of IMF.
*denotes the country in the OECD group, 19 sub-sample countries in this paper.# represented the country is the OECD member now because those four countries (Chile、Israel、South Korea, and Mexico) joined the OECD after 1993, be classified in mixed countries group. |
Appendix 3.
This study used the method of Katzur and Spierdijk (2013) to estimate expected and unexpected inflation with a AR (1) model. The inflation model and estimation as follows:
|
PIt=C1+C2PIt−1+εt∼AR(1)ExpectedPI=0.0351+0.9353PIt−1,UnexpectedPI=εt,R2=0.8874
|
The adoption of the AR (1) method could express the adaptive expectation theory, which presses up the Fisher equation concept. Adaptive expectations refers to people would use past information to expect future events.









 DownLoad:
DownLoad: