1. Introduction
The purging nut (Jatropha curcas L.) is a woody-shrub species belonging to the Euphorbiaceae family. Its true origin center is unknown, but studies indicate that the species is native to the countries of Central and South America [1]. In recent years, this species has researched to give commercial exploitation in biodiesel production [2,3,4]. J. curcas is easily propagated and it has a growth rate, short period until the first fruit harvest [5], low seed cost [6], high oil content (40–58%) [7,8], and good adaptation to different agroclimatic conditions [9], contributing to the wide geographical distribution of the plant, being present in practically all the intertropical regions of the world [9,10]. The physiological characteristics of the species, associated with its economic potential, can transform J. curcas into an alternative crop for arid and semiarid regions [11], because can be used to prevent and/or control erosion and in-land reclamation [12]. Some authors have described that the high market demand from markets for biodiesel has stimulated J. curcas plantations in many organizations, because renewable energy is important for sustainable environmental development [7,9,13,14,15]. J. curcas can contribute to carbon sequestration [7,16], reducing the greenhouse gas emissions and energy use; while my increase organic matter contents of the soils, the former due to lower costs are also characteristics attributed to this species [17]. While the aim of pro-poor development is to increase economic benefits to the poorer members of society, such development should not unduly threaten food or water security, reduce access to land or create poor working conditions. Pro-poor development should be specifically pro-women in order to address the gender imbalance of access to economic opportunities, health and education in developing countries to be sustainable; including the need for environmental sustainability and its cultivation is recommended by United Nations [18].
Leaf area (LA) is one of the six most important traits that drives plant form and function [19]. This descriptor has been widely used to describe a range of variables including growth, productivity, photosynthetic efficiency, soil characteristics including salinity and acidity, transfer and exchange of heat, carbon, nutrients and water, which in turn affect plant yield [20,21]. Thus, a correct determination of the LA becomes even more important in crop species, since the leaf is the organ of greater influence with the environment and it is through this that the agronomic studies are based on the important decision making.
Directly measure of individual LA are both, laborious, expensive as well a time consuming task and often constrained by logistical factors. Leaf area is traditionally quantified by direct methods, which are destructively or obtained through high-cost equipment, such as AM350 portable leaf area meter (ADC BioScientific Ltd., Hoddesdon, UK). With the intensification of modeling techniques, numerous studies have proposed allometric models to predict the LA in different species [21,22,23,24,25]. Hence, simple linear measurements like leaf length (L), leaf width (W) are used in allometric equations to predict the leaf area [26]. Further, such non-destructive methods like allometry have been preferred over traditional destructive ones [20]. However, in many studies the adequacy of the assumptions model to estimate the LA has not been carefully examined. With exception of PompelliAntunesFerreira et al. [21] all other papers used small samples to predict LA, without assessing their accuracy, showing many mistakes that already done in allometric models to predict LA.
Leaf development is genetically controlled [27]; however, the environment exerts pressures that should modify the foliar morphogenesis, and the degree of disturbance in leaf development can be as strong as the intensity of the environment [28,29]. Based on these findings, it could be argued that populations under the different environmental characteristics behave in different ways, making it difficult to group. Thus, a technique adopted to predict the foliar development of one population might not be applicable in another population, which would make the allometry process laborious. Nevertheless, leaves of J. curcas sampled in both rainy or drought may be similar morphologies may share a single allometric equation [21], feature that highlighted against environment disturbances. However, J. curcas is a species grows in many countries and with different ecosystems one may question whether a single equation, established for a single population (only northwestern Brazil), could be valid for all populations and for all macro environments around the world. In this sense, we decided to include in this study previously published [21] plants cultivated in other three ecosystems, including the center of origin of the species. For this reason, our main hypothesis is based on intraspecific variations of the J. curcas leaves; and, in this study, we reevaluate the equations previously proposed for this species [21], including three new genotypes to the allometric procedures. We are testing the feasibility of fitting a single allometric equation using the non-destructive measurements of J. curcas leaf area from three contrasting populations collected in two different countries, plus those samples in Brazil ones (for details, see PompelliAntunesFerreira et al. [21])
2. Material and methods
For model construction, ~500 healthy leaves were collected at least 20 healthy plants naturally grown at each locations, being Astrea, Cesar, Colombia (9°30′17′′N; 73°58′34′′W; 80 m asl); Barranca, Guajira, Colombia (10°57′37′′N; 72°49′28′′W; 192 m asl), and Mexico, cultivated in the Universidad de Córdoba, Montería, Cordoba, Colombia (8°47′26′′N; 75°51′16′′W; 14 m asl). To validate the model, an independent data set of 150 leaves were taken from each population as recommended by AntunesPompelliCarretero et al. [23]. All leaves were scanned using a scanner (Epson 1200 x 1200 dpi) and measured with the Image-Pro® Plus software, as described in Pompelli Antunes Ferreira et al. [21]. The leaves encompassed the broadest range as possible. The full range sampled leaves were presented in Table 1.
Table 1. Means ± standard deviations (SD), minimum (min) and maximum (max) values for the leaf length (L) and width (W) and leaf area (LA) of the three genotypes of Jatropha curcas L.
|
L (cm) |
W (cm) |
LA (cm 2) |
|
Mean ± SD |
Min |
Max |
Mean ± SD |
Min |
Max |
Mean ± SD |
Min |
Max |
| Astrea |
13.9 ± 4.6 |
2.0 |
24.2 |
16.8 ± 5.6 |
2.2 |
29.2 |
193.2 ± 98.6 a |
3.4 |
468.9 |
| Barrancas |
10.6 ± 4.7 |
3.1 |
23.1 |
12.1 ± 6.2 |
2.8 |
30.2 |
113.9 ± 108.3 b |
5.7 |
525.2 |
| Mexico |
11.9 ± 4.0 |
1.7 |
18.6 |
13.4 ± 4.9 |
1.4 |
22.7 |
117.6 ± 62.5 b |
1.4 |
285.1 |
Nine theoretical models (more widely used in the literature) were tested, based on different combinations between the components of LA (dependent variable) and respective values of L and W (independent variables). The equations were deduced by the principle of parsimony [30], and thus from the "simplest", or an "optimal" description of the data. All equations were adjusted following the linear simple, modified linear (from exclude β0) and power models (more information, see Table 2). All parameters of each model were obtained using DataFit version 8.0.32 (Oakdale Engineering, Oakdale, PA, USA). The statistical criteria used to select the models were based on (i) adjusted coefficient of determination (Radj2), (ii) mean squared error (MSE), (iii) Student's t-test (P < 0.001) for absolute mean of errors with confidence intervals [31], (iv) dispersion pattern of residuals in percentage terms (εi%) and the best relationship (major Radj2) between observed leaf area and estimated leaf area of the independent data set used to validating equations. The dispersion of the residues were observed in the total sample set, both in small leaves and in larger leaves. The hypothesis of normality of the errors were evaluated, so the heteroscedasticity was considered a reason for model disqualification. These procedures allowed us to assess the occurrence of bias and accuracy in all proposed models [32].
Table 2. Statistical models and equations to predict leaf area as a function of linear dimensions of leaves.
|
| (Model #1) |
Linear |
Yi=β0+β1∗Length+εi |
(1) |
| (Model #2) |
Linear |
Yi=β0+β1∗Width+εi |
(2) |
| (Model #3) |
Linear |
Yi=β0+β1∗(Length∗Width)+εi |
(3) |
| (Model #4) |
Linear without intercept |
Yi=β1∗Length+εi |
(4) |
| (Model #5) |
Linear without intercept |
Yi=β1∗Width+εi |
(5) |
| (Model #6) |
Linear without intercept |
Yi=β1∗(Length∗Width)+εi |
(6) |
| (Model #7) |
Power |
Yi=β0∗Lengthβ1+εi |
(7) |
| (Model #8) |
Power |
Yi=β0∗Widthβ1+εi |
(8) |
| (Model #9) |
Power |
Yi=β0∗(Length∗Width)β1+εi |
(9) |
| Yi = leaf area, β0 and β1 = model coefficients and εi= random error |
To quantify the extent and source of variability (intra- and intergenotypes), we performed the analyses of the variance from the components following the methods presented by MessierMcGill and Lechowicz [33]. Each characteristic was inserted into general linear mixed models of the 'nlme' package [34] and adjusted to obtain variation within and between species. Observations were nested within species and included as random factors. Variance components 'varComp' were used to measure the relative intraspecific variation of each genotype, and the variation of the morphometric components of the leaf, L, W and LA were used simultaneously adding to the variation in the parameter that specifies the change in leaf elongation (ratio between leaf length and leaf width), based on the following expression:
|
KΔi=(RSDL+RSDW+RSDLA+RSDstretching4)∗10
|
(10)
|
where: KDi = intraspecific variation in the genotype i; RSDL = relative standard deviation of leaf length, RSDW = relative standard deviation of leaf width, RSDLA = relative standard deviation of leaf area, and RSDstretching = relative standard deviation of leaf elongation (i.e., ratio between leaf length and leaf width).
Nevertheless, to compare leaves sampled from Colombia and Mexico with the sampled from Brazil, we performed several simulations with the model identity test for all possible combinations of populations to determine the degree of similarity of the coefficients of the particular and general models. Theoretically, if a particular allometric model presents the same coefficients (H0: β1 = β2 = ... βn), then the models are identical. The statistical test for the hypothesis H0: β1 = β2 = ... βn is based on the difference between the sum of squares (SS) of parameters of the general model [SSparameters (G)] and the particular model [SSparameters (P)], i.e., in the reduction that H0 causes in the sum of squares of parameters in the general model. When the analyses indicated the approval of a generalized model, we compared the predicted values of this model with a random sample containing leaf samples from all species (Student's t-test; P < 0.01).
3. Results
General profile of sampled leaves – Table 1 shows the spectrum of sampled leaves in each populations. It is verified that the leaves sampled from Mexico and from Barranca, although they present a similar mean of LA (Table 1; P ≥ 0.05), the amplitude of the leaves sampled in Barranca range from 5.7 cm to 525.2 cm, whereas the amplitude of the leaves sampled in Mexico range from 1.4 cm to 285.1 cm. On the other hand, the leaves sampled in Astrea are, on average, 69.6% and 64.3% higher than the leaves sampled in Barranca and Mexico. The same tendency shown above is fully translated for the other allometric variables of the leaf (length and width).
Astrea overview
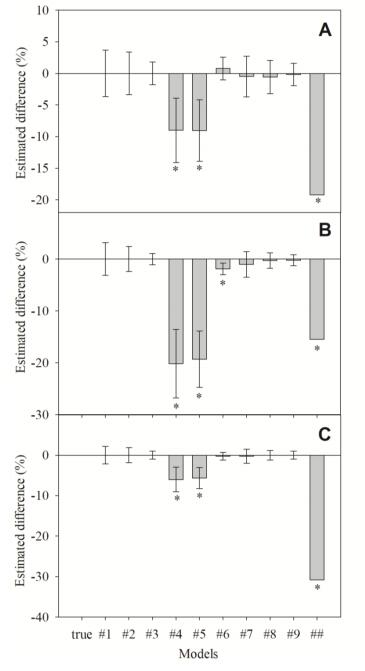
– All nine developed equations (Table 3) presented as good predictors of leaf area for Astrea genotype, since Radj2 was always higher than 0.908. Thus, at first glance, all proposed equation should be able to predict with accuracy the LA of Astrea genotype of J. curcas. However, when we analyzed the deviation between estimated leaf area and observed leaf area (Figure 1a), we demonstrate that equations #4, and #5 are biased, because cause a significant overestimation of LA. In this case, the overestimation can lead for ~14% of the estimated leaf area. It is also verified that the equation proposed by PompelliAntunesFerreira et al. [21] is not able to estimate with good precision the Astrea leaf area, since it leads to an overestimation in the order to 19% in the leaf area. All these equations had an estimated significantly difference different from zero (biased) and they were excluded from the further analysis.
Table 3. Statistical models, regression coefficients (β0, β1), degrees of freedom of residuals (R-d.f.), mean squared error (MSE), coefficients of determination adjusted for the degrees of freedom (Radj2) and P value as a function of linear dimensions of leaves for Jatropha curcas L.
| Models |
Coefficients |
R-d.f. |
MSE |
Radj2 |
P |
| β0 |
β1 |
| Astrea |
| #1 |
-91.832 |
20.528 |
439 |
890.818 |
0.908 |
< 0.001 |
| #2 |
-89.508 |
16.814 |
439 |
755.110 |
0.922 |
< 0.001 |
| #3 |
3.738 |
0.734 |
439 |
210.531 |
0.978 |
< 0.001 |
| #4 |
--- |
14.563 |
440 |
1,716.857 |
0.961 |
< 0.001 |
| #5 |
--- |
12.028 |
440 |
1,562.756 |
0.965 |
< 0.001 |
| #6 |
--- |
0.746 |
440 |
212.983 |
0.993 |
< 0.001 |
| #7 |
1.669 |
1.779 |
439 |
681.355 |
0.930 |
< 0.001 |
| #8 |
1.113 |
1.800 |
439 |
457.116 |
0.953 |
< 0.001 |
| #9 |
0.925 |
0.963 |
439 |
206.904 |
0.979 |
< 0.001 |
| Barrancas |
| #1 |
-125.038 |
22.648 |
499 |
742.941 |
0.937 |
< 0.001 |
| #2 |
-91.545 |
17.006 |
499 |
435.235 |
0.963 |
< 0.001 |
| #3 |
-4.146 |
0.759 |
499 |
84.732 |
0.993 |
< 0.001 |
| #4 |
--- |
12.708 |
500 |
3,267.911 |
0.866 |
< 0.001 |
| #5 |
--- |
11.027 |
500 |
2,205.731 |
0.909 |
< 0.001 |
| #6 |
--- |
0.744 |
500 |
92.400 |
0.994 |
< 0.001 |
| #7 |
0.584 |
2.151 |
499 |
458.460 |
0.961 |
< 0.001 |
| #8 |
0.828 |
1.896 |
499 |
162.648 |
0.986 |
< 0.001 |
| #9 |
0.600 |
1.037 |
499 |
84.911 |
0.993 |
< 0.001 |
| Mexico |
| #1 |
-59.816 |
14.916 |
532 |
383.114 |
0.902 |
< 0.001 |
| #2 |
-48.696 |
12.413 |
532 |
275.274 |
0.930 |
< 0.001 |
| #3 |
-1.230 |
0.667 |
532 |
78.454 |
0.980 |
< 0.001 |
| #4 |
--- |
10.393 |
533 |
742.704 |
0.956 |
< 0.001 |
| #5 |
--- |
9.200 |
533 |
550.063 |
0.967 |
< 0.001 |
| #6 |
--- |
0.662 |
533 |
78.629 |
0.994 |
< 0.001 |
| #7 |
0.777 |
1.986 |
532 |
245.092 |
0.937 |
< 0.001 |
| #8 |
0.810 |
1.878 |
532 |
116.795 |
0.970 |
< 0.001 |
| #9 |
0.593 |
1.020 |
532 |
78.181 |
0.980 |
< 0.001 |
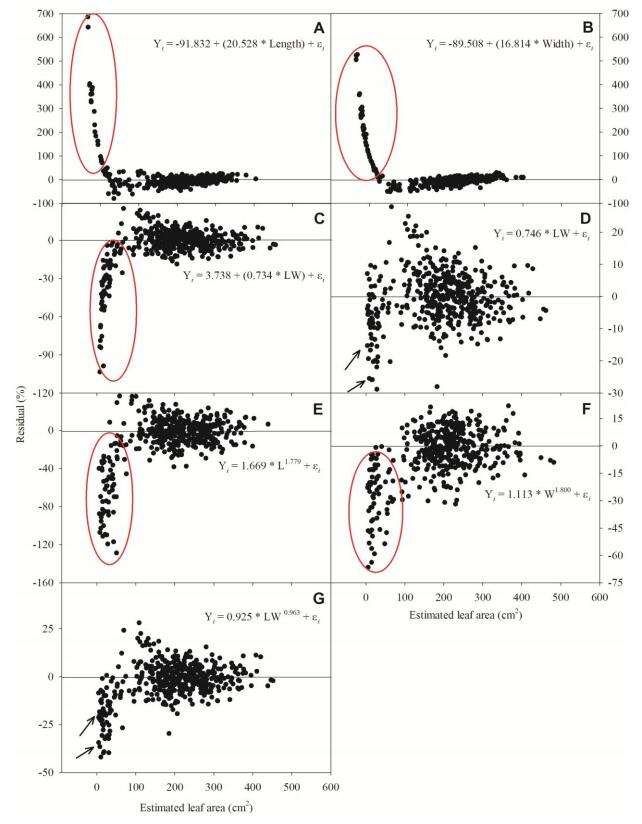
With the disqualification of equations #4, and #5, seven equations remained to be analyzed more in details. Thus, a deep analysis of relationship between estimated LA and dispersal pattern of residuals, revealed that equations #1 and #2 lead to overestimation or underestimation, respectively of 12.6% and 11.7% of the leaves (when considering relative errors ≥ 20%) (Figure 2). A possible source of error must be due to negative values of β0, that in these equations were bigger than -89.0; resulting in negative values of LA (i.e., invalid for biological condition). The heteroscedastic dispersal pattern of residuals of the model #3, was used to us to disqualify it, because this model lead to overestimation at least 10% of the leaves (when considering relative errors ≥ 20%), with residuals higher than 100%, in many times. The biased pattern of residuals showed in equations #1, #2 and #3 are as large as the smaller the sampled leaves. As shows in Figure 2, the equations #6 lead to overestimation from some samples of leaf areas. Therefore, this overestimation is lower than 2%, which cannot invalidate this equation.
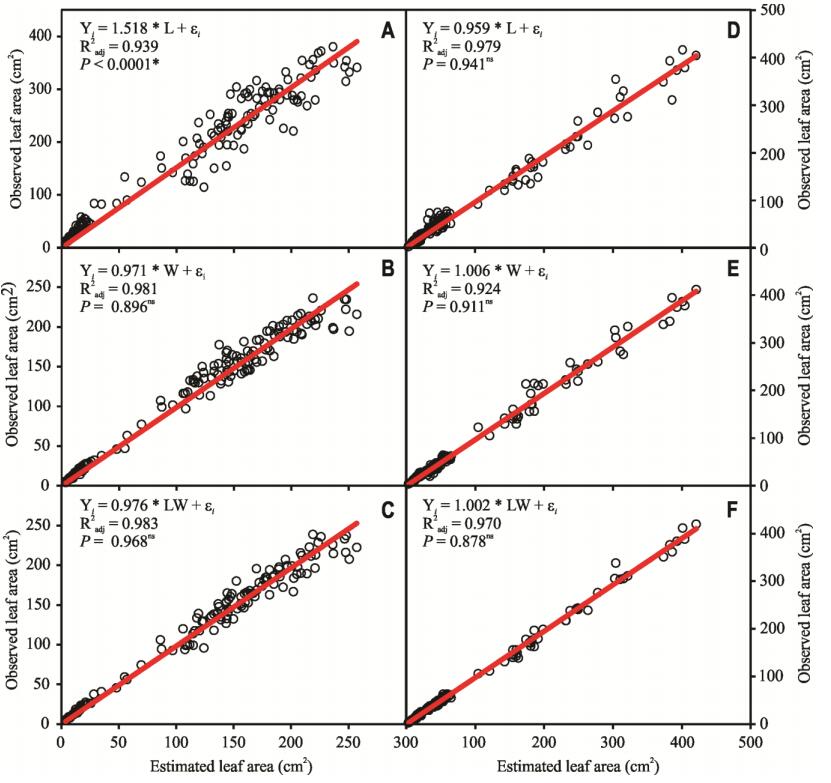
From nine initial proposed models, only four models (#6, #7, #8 and #9) were entirety approved. When we pooled the relationship between observed leaf area (LAo) and estimated leaf area (LAe) of the independent sample leaves (Figure 5, left panels), we verified that all equations returns good fit curves, showing the coefficient of determination above of 0.939. However, the equation #7 returns significant difference between LAo and LAe, and then was disqualified, resulting only three equations approved (#3, #8, and #9).
The higher KΔi of Astrea genotype (in order of 32%) lead to disqualify the linear model to predict LA in this genotype. Thus, only two equations remained (#8, and #9); both equations had higher Radj2, lower MSE and good fit of residuals (Figure 2); so both can estimate without bias the LA of Astrea genotype. However, equation #8 are less laborious than equation #9; this equation could also be an interesting option because it requires measurement of only one leaf dimension (i.e., leaf width), simplifying measurement procedures, an important aspect specially in field when a large number of leaves have to be monitored.
Barranca overview
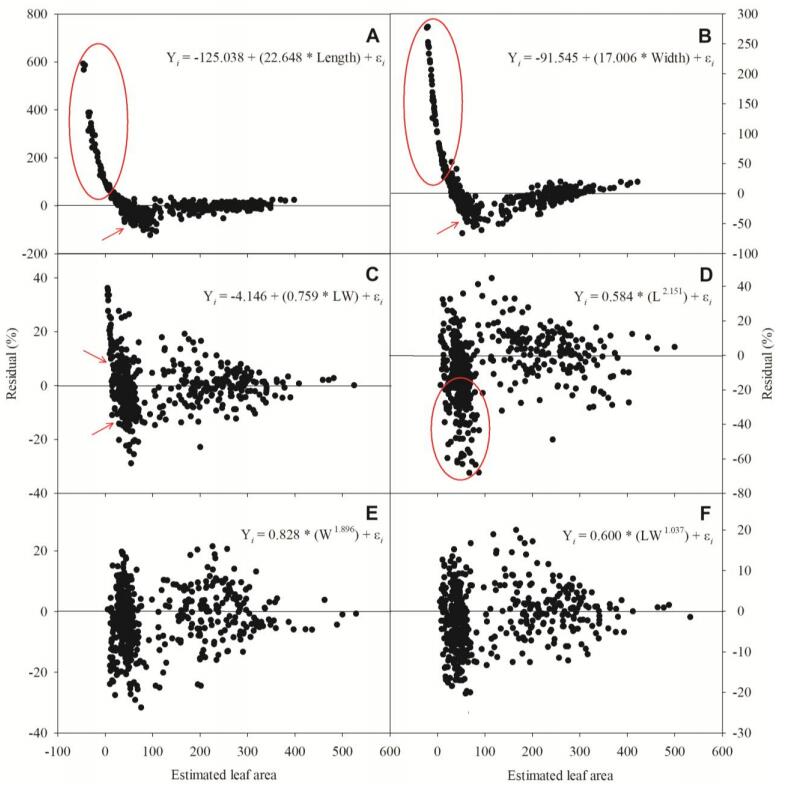
– Equally to Astrea genotype the Radj2 in Barranca genotype was higher than 0.866 (Table 3), with equations #4, #5, #6 are significantly (P ≤ 0.01) different from zero (biased) and then were excluded from the further analysis (Figure 1). Albeit that presented higher Radj2, the equations #1, and #2 were disqualified as well, because they present higher β0 value (higher than −91.0). From nine initial proposed models, only four models (#3, #7, #8, and #9) were entirety approved. The heteroscedastic dispersion of residuals showed in equation #3 leads to under or overestimation about from 2% to 4%, fact that do not permit it exclusion in the further analysis. Same situation was verified in dispersion of residuals from equation #7, where less than 10% of LAe was overestimated.
As the KΔi for Barranca genotype was very high (in order of 52%), the linear model #3 was disqualified, resulting in only three equations summarily approved. With higher Radj2, lower MSE and good fit of residuals, the equation #9 was considered the best equation to estimate LA for Barranca genotype. Both equation #7and #8 were approved too (Figure 5). However, the equation #8 are better than equation #7, because it present higher Radj2, lower MSE and good fit of residuals in comparison with the equation #7.
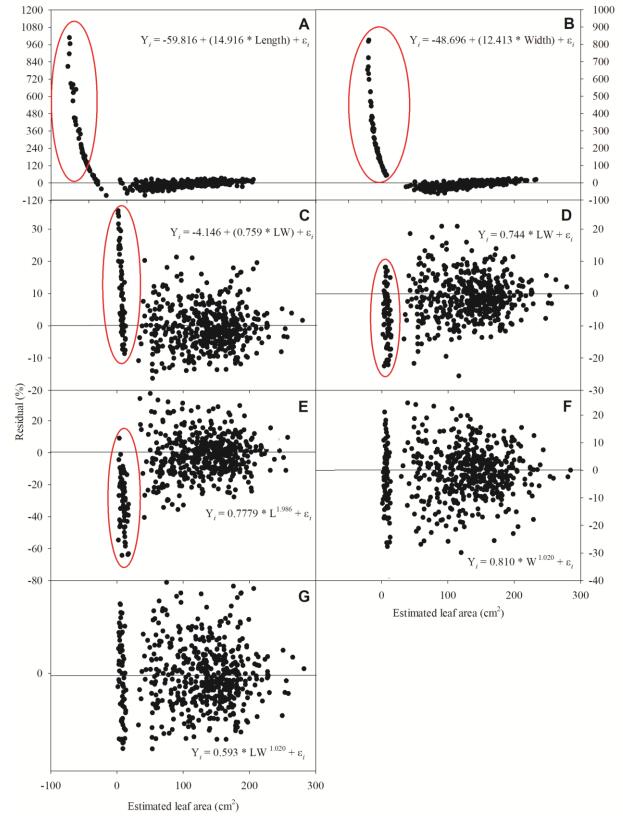
Mexico overview
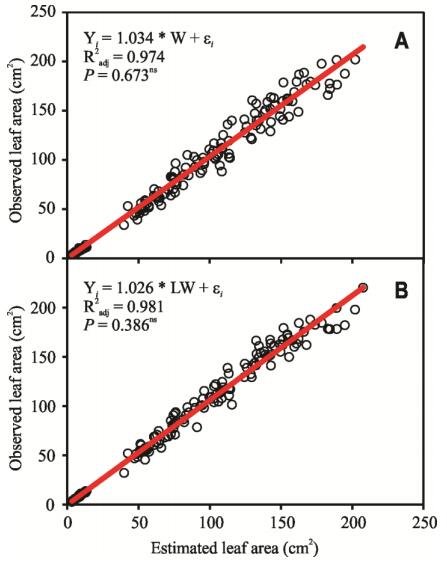
– In similar manner with the other populations, the Radj2 of Mexico genotype was higher than 0.902 (Table 3). Even if the amplitude of the estimated difference of Mexico population was lower than the other populations, equations #4 and #5 overestimate the LA significantly from the true leaf area (Figure 1c). Equations #1 and #2 were disqualified too because they present higher β0 value (higher than −48.7). From nine initial proposed models, only five models (#3, #6, #7, #8, and #9) were entirety approved. Thereupon, the analysis of residuals lead to disqualified the equations #3, #6, and #7, because they present a heteroscedastic residual dispersion behavior, leading to over or underestimate the LA from 13% to 15% (Figure 4). This higher heteroscedastic behavior was used to disqualify these models to predict LA in Mexico population. Thus, only two equations: #8 and #9 were summarily approved (Figure 4). In a similar manner to what was presented in Astrea population, the equation #9 is better to equation #8 (Figure 6), although the equation #8 are simplest than equation #9, because it requires measurement of only one leaf dimension (i.e., leaf width), simplifying the measurement procedures.
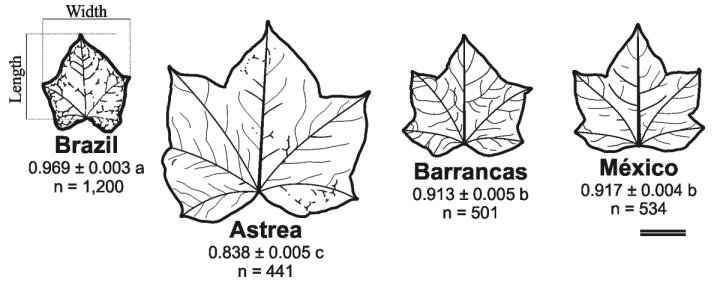
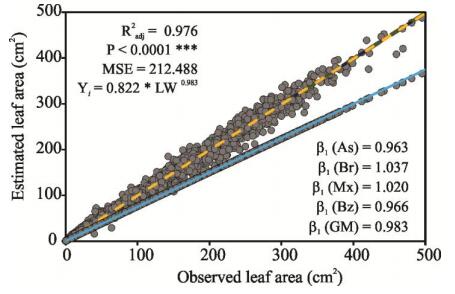
Morphological profiles and combined data on generalized model – As previously reported above, Barranca genotype have a similar L:W ratio than Mexico, while Astrea has the least L:W ratio to those studied. Compared to leaves sampled in Brazil, all other populations has the least L:W ratio, indicating the leaves from Mexico and Colombia are shorter and wider than those sampled in Brazil. Even though there is a significant variation in leaf size and L:W ratio, the leaves of all J. curcas genotype are apparently similar (Figure 7) in order to share several attributes, i.e., the leaves are palm-shaped, always tri- or penta-lobed. In thesis, these attributes may allow to grouping all population, and generate a single equation. To test this hypothesis, we test if β1 = β2 = ... βn. The analysis of variance for model identity test proved that b0 and β1 solved from equation #9 are identicals. The table of the hypothesis test for the generalized model, suggested that there were no significant differences among the coefficients of the specific models of the five populations (P > 0.01; F(6; 2,667) = 2.04ns; Table 4). Thereupon, we calculated the intra- and interspecific variance of all morphometric measurements of the leaves and shows that intraspecific differences accounted for 75.8%, 77.6%, 72.8% and 83.0% of variability for LA, L, W and RSDstretching, respectively, while interspecific variation represented 24.2%, 22.4%, 27.2% and 17.0%, respectively. These greater influences of intraspecific variability in the range of component values are reflected by higher KΔi values in all populations. Afterwards, we left the idea of considering each population in particular mode and proceeded to adopt a single grouping, containing all populations. This grouping generates a single allometric equation with the ability to predict without bias the leaf area of J. curcas independent of population. The equation is expressed by Yi = β0 *Xiβ1+ εi (Yi = 0.822 * LA0.983; Radj2 = 0.976, MSE = 212.488; Figure 8).
Table 4. Analysis of variance for model (Yi = β0 * xβ1) identity test for four Jatropha curcas L. populations in which x is the product of length and width. Both dependent and independent variables were log-transformed before analysis. Data derived from the calibration data set (n = 2,675 leaves). Source of variation (SV), degrees of freedom (d.f.), sum of squares (SS), mean squares (MS) and calculated F (Fcalc)*.
| SV |
d.f. |
SS |
MS |
Fcalc |
| Parameters |
8 |
12,237.066 |
--- |
|
| Reduction (βs') |
2 |
12,230.049 |
--- |
|
| Reduction (H0) |
6 |
7,017 |
1.170 |
2.04 |
| Residual |
2,667 |
1,529.68 |
0.574 |
|
| Total |
2,675 |
13,766.934 |
|
|
| *F1% (6; 2,667) = 2.81 |
4. Discussion
Many papers [21,35,36,37] describe allometric equations do predict LA of J. curcas. However, these studies did not consider the origin differences of J. curcas genotypes to be incorporated in to the model for leaf area estimation and so far, there has not been any research conducted for non-destructive LA estimation in J. curcas. Although PompelliAntunesFerreira et al. [21] proposed a single equation to predict the LA of plants grown in the dry and rainy, the leaves were collected from the same plants; therefore, disregarding the effect of the genotypes in their study. In the present study, we used three different genotypes from two different countries to test the viability of the equation proposed by PompelliAntunesFerreira et al. [21] in the effective prediction, without bias, of the LA in other genotypes of J. curcas. In fact, the equation proposed by PompelliAntunesFerreira et al. [21] was not effective; so that it was necessary to construct others allometric equations for each of the studied genotypes.
Thereupon, we concentrate all efforts to construct allometric equations to predict the leaf area for each genotypes. In a similar manner to describe in PompelliAntunesFerreira et al. [21] all genotypes studied here showed that power models, type Yi = β0 *Xiβ1+ εi, have good precision, leading to estimation in J. curcas leaf areas without bias. All linear models or power model, which use only one leaf dimensions were not approved for many reason, described above; but the main reason was the use of intercept, which can overestimate or underestimate the LA, if it is positive or negative, respectively. Although, the use of these equations could be recommended, but their use are efficient only when a stratification of the leaf size classes is performed, simultaneously checking the dispersion pattern of the residues in all classes of leaves, as suggested by others [21,23,32,38]. However, this "solution", sometimes becomes laborious and impractical, despite the ease of adjustment and operation of this type of model. Moreover, the linear models are even more biased than single-dimension power equations, especially in situations of high KΔi, as verified in all genotypes studied here. Simple linear models are often considered adequate to predict the LA of many agricultural and forestry species [22,24,26,39,40,41,42,43]. These models appear to operate with some loss in precision because of the violation of the underlying assumptions, resulting in serious statistical problems, e.g. weaknesses in the range of variation in the data and sample size. Some of these models describe only part of the leaf variations. In addition, the inflation of several numerical statistical parameters is quite common in very small samples. In this study, we showed that the application of all simple linear models could be questionable, especially for small leaf classes. This problem has already been mentioned by AntunesPompelliCarretero et al. [23] for different varieties of Coffea sp. and later was noted by PompelliAntunesFerreira et al. [21] for leaves of J. curcas. In these paper, we prefer not to test another allometric equations available for J. curcas [35,36,37], since they have already been considered biased by PompelliAntunesFerreira et al. [21].
In the model validation, correlation coefficients showed that there was a highly reliable relationship between LAo and LAe. Correlation coefficients between them for models using Astrea (Figure 5A–D), Barranca (Figure 5E–H) and Mexico (Figure 6) was very high, indicating that all the proposed equations are able to estimate without bias the leaf area of a new leaves samples.
The morphological profile of four J. curcas leaves studied here may seem to be distinct (Figure 7), the analysis of variance (Table 4) considering β1, indicates that all of them share a common pattern, a fact that is strongly demonstrated by the βs' reduction and Fcalc, which is less than the F1%. The dispersion diagram between LAo and LAe (Figure 8) of all individualized and grouped models also seem to share a pattern. In this sense, we argue that the use of a single allometric equation to predict the leaf area of J. curcas, independent of the genotype used, is very possible and highly recommended, as this would avoid the construction of allometric equations for each of the studied genotypes; as well as attenuate the need for new allometric equations for other genotypes not studied here.
5. Conclusions
In this work, allometric models (the L*W power model without intercept) were developed to estimate the leaf area of four Jatropha curcas L. genotypes. Independently of genotype, this model can be used as a good tool to measure leaf area of genotypes of J. curcas. For each genotype, several allometric equations were generated and model type Yi = β0 *Xiβ1+ εi was validated as the best for all genotypes. In spite of this, a single equation, joining all the genotypes, was developed (Yi = 0.822 LW0.963), which greatly simplifies the process of measuring the leaf area of the genotypes. This unique equation showed an effectiveness of 97.6%, a fact that should be highlighted. This is very important especially when successive leaf area measurements are needed. Such models can simply and accurately estimate leaf area without the use of expensive instruments such as LA meter, digital camera, and scanner with image measurement software. This paper has shown that it is possible to come up with a single equation for Jatropha curcas, but also showed that Jatropha curcas can be an alternative to agriculture with the use of crop management, crops and fertilizers, increasing farmer income and reducing soil erosion using intercropping with crop plants. The fact that Jatropha curcas is quite resistant to water scarring and the possibility to bring income and input to small farmers in semiarid areas.
Acknowledgements
The authors thank the National Council for Scientific and Technological Development (CNPq Grants 404357/2013-0). The authors would also like to anonymous reviewers for their kind revisions of this manuscript.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: