Figure 1.
Development of XU100 and COVID-19 pandemic. Source: Bloomberg Terminal; MHT, 2020.
Citation: Mustafa Tevfik Kartal, Özer Depren, Serpil Kılıç Depren. The determinants of main stock exchange index changes in emerging countries: evidence from Turkey in COVID-19 pandemic age[J]. Quantitative Finance and Economics, 2020, 4(4): 526-541. doi: 10.3934/QFE.2020025
| [1] | Mustafa Tevfik Kartal . The behavior of Sovereign Credit Default Swaps (CDS) spread: evidence from Turkey with the effect of Covid-19 pandemic. Quantitative Finance and Economics, 2020, 4(3): 489-502. doi: 10.3934/QFE.2020022 |
| [2] | Raéf Bahrini, Assaf Filfilan . Impact of the novel coronavirus on stock market returns: evidence from GCC countries. Quantitative Finance and Economics, 2020, 4(4): 640-652. doi: 10.3934/QFE.2020029 |
| [3] | Selahattin Kaynak, Aykut Ekinci, Havvanur Feyza Kaya . The effect of COVID-19 pandemic on residential real estate prices: Turkish case. Quantitative Finance and Economics, 2021, 5(4): 623-639. doi: 10.3934/QFE.2021028 |
| [4] | Cunyi Yang, Li Chen, Bin Mo . The spillover effect of international monetary policy on China's financial market. Quantitative Finance and Economics, 2023, 7(4): 508-537. doi: 10.3934/QFE.2023026 |
| [5] | Korhan Gokmenoglu, Baris Memduh Eren, Siamand Hesami . Exchange rates and stock markets in emerging economies: new evidence using the Quantile-on-Quantile approach. Quantitative Finance and Economics, 2021, 5(1): 94-110. doi: 10.3934/QFE.2021005 |
| [6] | Rubaiyat Ahsan Bhuiyan, Tanusree Chakravarty Mukherjee, Kazi Md Tarique, Changyong Zhang . Hedge asset for stock markets: Cryptocurrency, Cryptocurrency Volatility Index (CVI) or Commodity. Quantitative Finance and Economics, 2025, 9(1): 131-166. doi: 10.3934/QFE.2025005 |
| [7] | Lorna Katusiime . Time-Frequency connectedness between developing countries in the COVID-19 pandemic: The case of East Africa. Quantitative Finance and Economics, 2022, 6(4): 722-748. doi: 10.3934/QFE.2022032 |
| [8] | Emmanuel Assifuah-Nunoo, Peterson Owusu Junior, Anokye Mohammed Adam, Ahmed Bossman . Assessing the safe haven properties of oil in African stock markets amid the COVID-19 pandemic: a quantile regression analysis. Quantitative Finance and Economics, 2022, 6(2): 244-269. doi: 10.3934/QFE.2022011 |
| [9] | Anouar Ben Mabrouk, Sabrine Arfaoui, Mohamed Essaied Hamrita . Wavelet-based systematic risk estimation for GCC stock markets and impact of the embargo on the Qatar case. Quantitative Finance and Economics, 2023, 7(2): 287-336. doi: 10.3934/QFE.2023015 |
| [10] | Fabrizio Di Sciorio, Raffaele Mattera, Juan Evangelista Trinidad Segovia . Measuring conditional correlation between financial markets' inefficiency. Quantitative Finance and Economics, 2023, 7(3): 491-507. doi: 10.3934/QFE.2023025 |
The development of countries depends on mainly the improvement of both the real and financial sectors. The main role of financial sectors is to finance economic activities in countries. Therefore, it could be said that financing has an important role in the development of countries.
All countries including both developed and emerging have been trying to sustain economic growth by providing monetary (finance) resources for commercial activities. However, unlike developed countries, emerging countries need much more financing.
Countries can provide financing from internal (national/domestic) and external (international/foreign) sources. Foreign sources become important when domestic savings are not sufficient. Thus, the condition of emerging countries is such. Therefore, emerging countries have been trying to increase foreign direct investments and portfolio investments (Karikari, 1992; Zengin et al., 2018).
Achieving financial stability through stabilizing fiscal, monetary (price), macroeconomic, and macro prudential indicators is quite significant in stimulating foreign investments. Foreign investors consider country risks in allocating funds among different asset opportunities to benefit from diversification (Dooley & Hutchison, 2009; Yang et al., 2018) by considering that the world has been making countries much more interdependent and this increases risks. In this context, there are a variety of indicators like credit default swap (CDS) spreads, foreign exchange rates (FER), foreign investors' shares and net buying amount in equity markets, interest rates, oil prices, etc. All of these indicators are significant in terms of roles and effects in economies (Orhan et al., 2019) for the development of emerging countries by affecting foreign investors' decisions. Therefore, activities of foreign investors are expected to make effects on the countries' (Hargis & Ramanlal, 1997; Bekaert & Harvey, 2003; Gümüş, 2010), stock exchange indices. Although increasing foreign direct investments is not so easy because it is related to so many geopolitical and political issues, stimulating foreign portfolio investments via bonds, bills, and equities is much easier.
On the other hand, COVID-19 is a very recent phenomenon that affects all countries deeply. It was originated from China, became pandemic at the beginning of 2020, and has been spreading all over the World. There are nearly 5.3 million cases, and 344 thousand deaths because of COVID-19 pandemic as of 05.24.2020 (World Health Organization (WHO), 2020). As a result of the pandemic, Turkey has been met with COVID-19 in March. The first case has been announced on 03.10.2020 officially, and the first death has occurred on 03.17.2020 in Turkey (Ministry of Health of Turkey (MHT), 2020). In such an environment, all economic and financial indicators have been deteriorating in the world and Turkey as well. Therefore, the COVID-19 pandemic normal should be considered in any analysis, especially related to macroeconomic and financial issues which are very sensitive risky conditions.
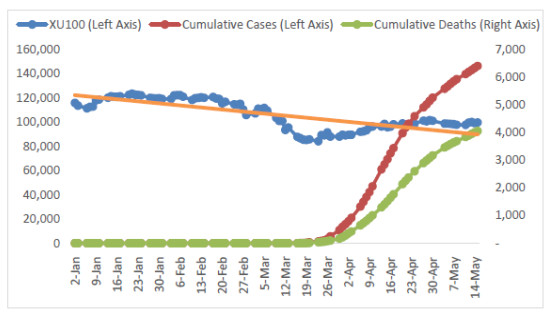
As a leading and pioneering country among emerging countries, Turkey has also foreign investments and has been suffering from COVID-19 pandemic. Figure 1 shows the development of the main stock exchange index (i.e. XU100), cumulative cases, and deaths resulting from the COVID-19 pandemic in Turkey.
As Figure 1 presents, the XU100 index has been decreasing since the beginning of 2020. Also, the index has been relatively high in the pre-pandemic and low in the pandemic period which started on 03.10.2020 in Turkey with the detection of the first case. Numbers of total cases have reached 146.5 thousand and the numbers of total deaths are around 4 thousand as of 05.15.2020 in Turkey.
With the occurrence and spreading of COVID-19 pandemic, Turkey has begun to take fiscal, monetary, and administrative precautions to decrease the negative effects on the economy, the state, corporations, households, and individuals. Some of the measures taken could be summarized as local lockdowns, quarantines on residential areas, closure of schools, ban on flights, lowering the minimum payment requirements of credit cards, cash transfers to families in need, increasing the amount of funding markets by CBRT including buying governmental bonds, deferred credit payments to banks, deferred tax and social security premium payments in various sectors, minimum wage subsidies, and ban on short sell in Borsa İstanbul (BIST) equity market as well (Morgan Stanley, 2020; Official Gazette, 2020).
First stock exchange in Turkey was established in 1985 under the name of Istanbul Stock Exchange (ISE). In 2013, BIST was established with the merger of ISE, Istanbul Gold Exchange and Futures and Options Exchanges (BIST, 2020a). With the effects of merger, BIST has been developing. For example, market value has reached TL 1233 billion as of 2020 June end whereas it was TL 505.9 billion as of 2013 end which multiplies 2.4 times. Also, total traded value has reached TL 2336.8 billion as of June end in 2020 whereas it was TL 816.8 billion in 2013. Besides, average traded value has become TL 18.8 billion as of June end in 2020 whereas it was TL 3.3 billion in 2013 (BIST, 2020b). In addition, an increasing traded volume since 2020 May has been seen in BIST equity market. Moreover, there are a variety of indices in BIST. However, BIST 100 is the main index symbolized as XU100 (BIST, 2020b).
By taking into consideration all information above, Turkey has been in the COVID-19 pandemic condition, there have been cases and deaths resulting from the COVID-19 pandemic, and the main stock index has been decreasing and it has been in low-level. Low-level index causes the underpricing of Turkish assets and this condition is negative for the country. Therefore, it would be beneficial to examine which factors cause the change of main stock exchange index in the COVID-19 pandemic period and whether these factors vary according to period whether Turkey is in either pre-pandemic period or pandemic period. Such a determination would contribute to regulatory bodies to develop policies to prevent the negative effects and hence stimulate foreign portfolio investments to Turkey via equities. Hence, Turkey can provide much more foreign portfolio inflows.
The study aims to define the effective factors causing changes in the main stock exchange index in Turkey in the pre-pandemic period and pandemic period by applying by performing random forest and support vector machine algorithms. Daily data between 01.02.2020 and 05.15.2020, 14 variables (including global, country-level, and market indicators), and the presence of COVID-19 are used for this aim. The study focuses on examining Turkey because the main stock exchange index has decreased at an important amount on average since the beginning of 2020. The study defines that the most influential factors are the retention amount of foreign investors in the equity market and CDS spreads in the pre-pandemic period. On the other hand, MSCI emerging markets index and volatility index has the highest significance in terms of change on XU100 index. Moreover, the net buying amount of foreign investors in the equity market does not affect throughout the periods examined whereas all other 13 variables have effects. The results of the analysis show the crucial effect of the COVID-19 pandemic for the changing of Turkey's main stock exchange index.
The main contributions of the study are that the study (ⅰ) is one of the pioneer study in Turkey examining the effects of COVID-19 pandemic on main stock exchange index, which is an important issue in finance and capital markets; (ⅱ) performs random forest and support vector machine algorithms that have been only a limited number of studies about this subject in the literature; (ⅲ) examines the determinants of XU100 index by using a large of indicators including global, country-level, market, and COVID-19 presence as well; (ⅳ) considers daily data from 01.02.2020 to 05.15.2020 which covers the pre-pandemic period and pandemic period in the same study.
The remain sections of the study are organized as follows. Section 2 summarizes variables that are used in the analysis, provides data descriptions, and explains the theoretical background of random forest and support vector machine algorithms performed in the study. Section 3 shows the analysis results. Section 4 presents findings-based discussion and conclusion.
In the literature, different variables affect stock exchange indices. They could be mainly categorized under 3 groups, which are global-level, country-level, and market variables.
The first group of studies focuses on the relationship with global variables. MSCI emerging markets index, oil prices, and the volatility index (VIX) take place in this group. A variety of studies take into consideration equity market prices and equity indices. Cremers et al. (2008), and Zhang et al. (2009), and Yang et al. (2018) include these variables in their studies. For example, Yang et al. (2018) use the MSCI index as a determinant. Hence, MSCI emerging market index is expected to be effective on the XU100 index since Turkey is an emerging country, and the MSCI emerging market index would be an important indicator for Turkey. When the MSCI index increases, then interest to Turkey also increases, and a positive relationship is expected between the XU100 index and MSCI index in turn. On the other hand, Turkey is expected to be negatively affected by oil prices Demir (2019) since Turkey is an oil importer country. Similarly, VIX index would make a negative effect on main stock exchange indices because the fear on capital markets also increases, and fund outflows from emerging countries increase when VIX index increases (Liew et al., 2018). For this reason, a negative relationship is expected between the XU100 index and the VIX index.
The second group of studies focuses on the relationship with country-level variables. In this group, there are CDS spreads, net funding amount of CBRT, securities amount held by CBRT, Treasury bond interest rates, Turkish Lira (TL) reference interest rate (TLREF), and USD/TL FER variables. Alexander & Kaeck (2008), Cremers et al. (2008), Zhang et al. (2009), Galil et al. (2014), Lahiani et al. (2016), Shahzad et al. (2017), and Kartal (2020) examine the relationship between equity indices and CDS spreads and determine a significant relationship. By considering these studies, a negative relationship is expected between the XU100 index and CDS spreads of Turkey. Clark & Berko (1997), Hajilee & Al Nasser (2014), Naik & Padhi (2014), Demir (2019), and Erdoğan et al. (2019a) include FER, Treasury bill, and short-term interest rate as independent variables in their study and define the negative relationship between stock index and these variables. Following this study, Treasury bond interest rates, TLREF, and USD/TL FER are included as a dependent variable to examine the XU100 index and a negative relationship is expected between the XU100 index and these variables as well. Besides, CBRT has been expanding its financial activities to support the economy in COVID-19 age. Therefore, we think that the main indicators of CBRT would be influential on the XU100 index. While Erdoğan et al. (2019b) use reel money supply as a variable, we consider two main indicators which are net funding amount of CBRT and securities amount held by CBRT in the context of main CBRT indicators. In case of increasing net funding amount and securities amount held by CBRT, there could be stability in the financial system and the increasing demand for equities. Hence, we expect a positive relationship between XU100 and these variables.
The third group of studies focuses on the relationship with market variables. This group includes equity market traded value, foreign investors' share in traded value, foreign investors' share in retention, retention amount of foreign investors in the equity market, and net buying amount of foreign investors. In literature, there are some studies that focus on the effects of foreign investors and foreign portfolio investments on equity markets and equity indices. For example, Bekaert & Harvey(1995, 1998), Clark and Berko (1997), Kim & Singal (2000), Choe et al. (1999), Kim & Wei (2002), McLean & Shrestha (2002), Tabak (2003), Adabag & Ornelas (2004), Dahlquist & Robertsson (2004), Nam (2004), Baklacı (2007, 2008), Akar (2008), Boyer & Zheng (2009), Gümüş (2010), Somuncu & Karan (2010), Vergil & Karaca (2010), İskenderoğlu & Karadeniz (2011), Elmas (2012), Sevil et al. (2012), Bolaman Avcı (2015), Soumaré & Tchana (2015), Vo (2015), Kesik et al. (2016), Liew et al. (2018), Demir (2019) and Topaloğlu et al. (2019) examine various phenomena related with foreign direct inflows, foreign portfolio inflows, foreign investors, foreign trading, and net buying amount of foreign investors in, especially emerging economies. They determine that some of the foreign trading phenomena are beneficial while others are not; foreign investors decrease the volatility in the long-run and make the equity market more efficient; the equity market index increases when foreign inflows increase. By considering these studies, it is expected that different indicators of foreign investors' activities could be influential on XU100. In this context, four different indicators, which are foreign investors' share in traded value, foreign investors' share in retention, retention amount of foreign investors in the equity market, and net buying amount of foreign investors, are taken into account in the analysis as dependent variables. Also, equity market traded value is added as a variable (Gümüş, 2010; Lee & Chung, 2018; Naufa et al., 2019) because the XU100 index is calculated based on equities which are traded in the equity market. For this reason, equity market traded value would be important. By the studies in the literature, a positive relationship is expected between the XU100 index and these variables.
In addition to these variables taking place in 3 groups, we consider the presence of COVID-19 pandemic in the analysis because the pandemic is a breaking point for all developed and emerging countries and Turkey as well.
On the other hand, this study includes the period between 01.02.2020 and 05.15.2020. This period is selected to focus on the very recent period including in time of COVID-19 pandemic and the nearest times before COVID-19 in 2020. For this reason, daily data is considered in the study. Data for only weekdays is considered because data for some variables like XU100, USD/TL FER, and net buying amount of foreign investors etc. could not be obtained for weekends. Therefore, weekend and official holidays are excluded from the analysis. Data for all variables are gathered from Bloomberg Terminal, CBRT (2020), MHT (2020), and Central Securities Depositories of Turkey (CSD, 2020) via email.
As dependent variable, daily closing values of XU100 index are used by following the studies of Gümüş (2010), Elmas (2012), and Kesik et al. (2016). That is why because we focus on the changes of XU100 level rather than changes in daily return. Moreover, Table 1 summarizes the details of all variables which are included in the study.
| Group | Variable | Symbol | Description | Effect | Data |
| Dependent | BIST Main Index | XU100 | Trading Day Closing Value of XU100 | N/A | Bloomberg |
| Global | MSCI Emerging Market Index | MXEF | MSCI Emerging Market Index | + | Bloomberg |
| Volatility Index | VIX | Chicago Board Options Exchange Volatility Index | - | Bloomberg | |
| Oil Prices | OIL | Crude Oil Prices (TL) | - | Bloomberg | |
| Country Level | CDS Spreads | CDS | 5-Years Sovereign CDS Spreads of Turkey | - | Bloomberg |
| Treasury Bond Interest Rates | DIBS | 1-Year Treasury Bond Interest Rate of Turkey (%) | - | Bloomberg | |
| USD/TL FER | USDTL | USD/TL Foreign Exchange Rate | - | CBRT | |
| TL Reference Interest Rate | TLREF | Daily TL Reference Interest Rate (%) | - | CBRT | |
| CBRT Net Funding Amount | CBRT_FUND | Net Funding Amount to Market Provided by CBRT | + | CBRT | |
| CBRT Securities Amount | CBRT_SEC | Net Amount of Securities Held by CBRT | + | CBRT | |
| Market | Equity Market Traded Value | EMVOL | Daily Equity Market Traded Value | + | Bloomberg |
| Foreign Investors' Share in Traded Value | ISHARE | Share of Foreign Investors in Traded Value | + | CSD | |
| Foreign Investors' Share in Retention | FSHARE | Equity Retention Rate of Foreign Investors | + | CSD | |
| Retention Amount of Foreign Investors in Equity Market | FAMOUNT | Retention Amount of Foreign Investors in Equity Market | + | CSD | |
| Foreign Investors' Net Buying Amount | NETBUY | Net Buying Amount of Foreign Investors | + | CSD | |
| COVID-19 | COVID-19 Presence | CVD | 1: If COVID-19 exists; 0: otherwise | - | MHT |
| Note: N/A means that not applicable since this is dependent variable. Positive (+) relationship means that XU100 increases when independent variables increase. Negative (-) relationship means that XU100 decreases when independent variables increase. |
|||||
DownLoad:
CSV
The daily data (workdays) between 01.02.2020 and 05.15.2020 was obtained from various sources in the study. The dataset was split into two periods, which were named as the pre-pandemic period and the pandemic period. Thus, the effects of independent factors on the XU100 index in both the pre-epidemic and the pandemic periods were able to be measured. Since the first COVID-19 case appeared on 03.10.2020 in Turkey, the pre-pandemic period represents the data between 01.02.2020 and 03.09.2020. Also, the pandemic period includes data between 03.10.2020 and 05.15.2020.
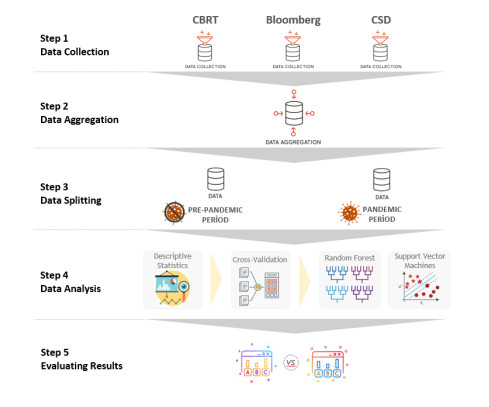
The model was constructed in five different steps. The flowchart of the proposed model is detailed in Figure 2.
The methodology steps of this study are as follows: the first step of the methodology was to obtain the data used in this study from different data sources. The second step was to agammaegate the datasets obtained and created one combined dataset which was ready to analyze. In the third step, the dataset was split into two groups to analyze the effects of independent variables on the XU100 index in both the pre-pandemic and the pandemic periods. Random Forest and Support Vector Machines algorithms with a cross-validation approach were used for both datasets in the fourth step. In the final step of the methodology, results obtained from the pre-pandemic and the pandemic periods were evaluated.
Nowadays, machine learning algorithms are widely used in almost every research area such as banking, finance, and economics. Random Forest and Support Vector Machines are the most common machine learning algorithms in the literature. Besides, other machine learning algorithms such as k-Nearest Neighbors, Naïve Bayes, and Neural Networks are used for different real-life problems.
There are two major ensemble learning methods for classification or regression tree algorithms, which are boosting and bagging (Shapire et al., 1998; Breiman, 1996). In 2001, the new algorithm, which is named as Random Forest, is proposed by Breiman as an upgraded version of bagging learning (Breiman, 2001). The algorithm steps of Random Forest are as follows (Wiener & Liaw, 2002):
1. Select n sample randomly from the dataset, which is named as ntree.
2. For each of the samples, construct an unpruned decision tree with the following modification. In each tree, select the number of predictors randomly (mtry) and choose the best split from among those predictors.
3. Predict the target variable by agammaegating the predictions of the trees.
On the other hand, Support Vector Machines is proposed firstly in 1992 for classification and regression problems (Vapnik, 1995; Vapnik et al., 1998). The Support Vector Regression uses cost function (e-intensive loss function) to minimize regression error. The optimization problem is defined as in Equation 1 (Law & Shawe-Taylor, 2017).
objective:
| minw,b12‖w‖2+C∑ni=1(ξ+i+ξ−i) | (1) |
subject:
| yi−w.xi−b≤ϵ+ξ+i | (2) |
| w.xi+b−yi≤ϵ+ξ−i | (3) |
| ξ+i,ξ−i≥0∀i | (4) |
The first term of the objective function represents the regularization constraint to prevent over-fitting and the second term is the ε-insensitive loss function. ξ+i,ξ−i represents the slack variables in the optimization problem.
One of the most important parts of a machine learning approach is to set a training dataset, where the model is enhanced, and testing datasets, where the model results are tested, to prevent overfitting/underfitting problems. In a machine learning algorithm, there are no strict assumptions such as stationarity, correlation, and cointegration between variables. This is the strongest aspect of the machine learning approach. In this study, a k-fold with t-repeat cross-validation approach was performed to avoid overfitting/underfitting problems. With this approach, the dataset was randomly separated into k equal sized subsamples. k-1 sub-samples were used as training datasets while one sub-sample was used as a testing dataset. The k estimations were used to produce a single estimation (Hastie et al., 1996). This process was repeated t times to obtain robust results. In this study, 5-fold with a 5-repeat cross-validation approach was applied to avoid overfitting/underfitting problems in the model.
Table 2 presents the descriptive statistics for determinants which is important to understand the basic characteristics of the dataset.
| Pre-Pandemic Period | Pandemic Period | Independent Sample t-test | |||||
| Mean | SD | Mean | SD | Sig. (2-tailed) | |||
| XU100 | 117.362 | 4.932 | 94.743 | 5.272 | 0.000 | ||
| MXEF | 1.090.6 | 43.7 | 872.8 | 44.0 | 0.000 | ||
| VIX | 19.4 | 10.2 | 47.4 | 14.7 | 0.000 | ||
| OIL | 349.4 | 36.1 | 168.1 | 25.5 | 0.000 | ||
| CDS | 280.2 | 43.5 | 577.9 | 62.4 | 0.000 | ||
| DIBS | 11.1 | 0.8 | 10.1 | 1.4 | 0.000 | ||
| TLREF | 11.1 | 0.5 | 9.3 | 0.8 | 0.000 | ||
| USDTL | 6.0 | 0.1 | 6.7 | 0.3 | 0.000 | ||
| CBRT FUND | 6.348 | 3.793 | 16.870 | 3.608 | 0.000 | ||
| CBRT SEC | 3.225 | 100 | 5.944 | 2.332 | 0.000 | ||
| EMVOL | 3.006 | 583 | 2.367 | 516 | 0.000 | ||
| ISHARE | 24.8 | 3.2 | 20.7 | 5.3 | 0.000 | ||
| FSHARE | 0.61 | 0.02 | 0.59 | 0.02 | 0.000 | ||
| FAMOUNT | 49.678 | 4.826 | 35.435 | 2.388 | 0.000 | ||
| NETBUY | -35.8 | 54.0 | -48.3 | 30.9 | 0.173 | ||
| SD: Standard Deviation. | |||||||
DownLoad:
CSV
In Table 2, the XU100 index was 117,362 on average in the pre-pandemic period but it decreased to 94,743 level in the pandemic period. MSCI emerging country index, oil prices, Treasury bond interest rates, TL reference interest rate, equity market traded value, foreign investors' share in traded value, amount of foreign investors in the equity market, foreign investors' share in retention, and foreign investors' net buying amount decreased in the pandemic period compared to the pre-pandemic period. On the other hand, the Volatility index, CDS, USD/TL foreign exchange rate, CBRT net funding amount, and CBRT security amount increased in the epidemic period compared to the pre-epidemic period. An independent sample t-test was performed for each factor to measure whether the gap between the pre-pandemic and the pandemic periods has changed significantly. It was revealed that the average values of all factors in the pandemic period have significantly changed based on the pre-pandemic period, except for the net buying amount.
The goodness of fit criteria such as R2, Root Mean Square Error (RMSE), and Mean Absolute Error (MAE) was evaluated to choose the best performing model among the models that have a continuous dependent variable. These statistics are given in Table 3 for both Random Forest and Support Vector Machines algorithms.
| Pre-Pandemic Period | Pandemic Period | ||||||
| Methods | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| Support Vector Machine | 94.3% | 1216.28 | 992.34 | 96.8% | 1021.78 | 749.80 | |
| Random Forest | 93.6% | 1478.50 | 1131.91 | 95.8% | 1163.57 | 908.61 | |
DownLoad:
CSV
Based on Table 3, although the R2 values of both algorithms are quite high, the Support Vector Machines algorithm has a higher R2 and lower RMSE and MAE values than the Random Forest algorithm in both periods. Thus, it was decided that Support Vector Machines algorithm details are interpreted.
The term variable importance analysis is used to measure the effect size of the independent variables on the dependent variable. Variable importance for Support Vector Machines algorithms is given in Figure 3.
In the pre-pandemic period, the top 3 factors affecting the XU100 index were determined as retention amount of foreign investors in the equity market (FAMOUNT), CDS spreads, and Treasury bond interest rate (DIBS). Since the COVID-19 pandemic affected all sectors such as health, finance, production, and education, the priorities in these sectors and the importance of all factors that sustain these sectors have been changed. Thus, as expected, the top 3 factors affecting the XU100 index in the pandemic period have changed as MSCI emerging market index (MXEF), VIX index, and retention amount of foreign investors in the equity market (FAMOUNT). The importance of CDS spreads decreased from 2 in the pre-pandemic period to 12 in the pandemic period. On the other hand, the importance of MSCI emerging market index and CBRT Securities Amount (CBRT_SEC) increased to 1 and 4 from 4 and 11, respectively.
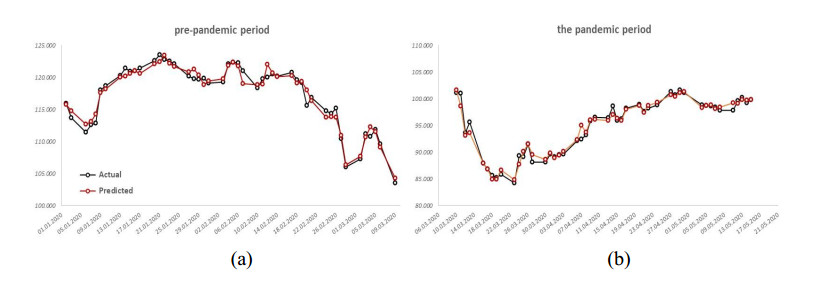
The actual and predicted values of the XU100 index predicted from the Support Vector Machines algorithm are given in Figure 4.
The actual and predicted values obtained from the support vector machines algorithm of the XU100 were very close real values of the XU100 index in both periods. Furthermore, the model was able to predict sudden increases or decreases very well.
In the study, the determinants of the main stock exchange index (XU100) changes in Turkey in the COVID-19 pandemic age were analyzed. In this context, daily data between 01.02.2020 and 05.15.2020, which includes pre-pandemic and pandemic periods, was used. Also, 14 variables were defined to be used in the analysis by reviewing the present literature. These variables could be classified under 3 groups as global-level, country-level, and market-level. The global group includes 3 variables, the country-level group includes 6 variables while the market-level group includes 5 variables. After collecting data from various data sources and splitting all data into two sub-period as pre-pandemic period and pandemic period, the performance of machine learning algorithms was compared and it was defined that the Support Vector Machine algorithm had higher prediction accuracy concerning Random Forest algorithms in both pre-pandemic and pandemic period. Therefore, the results of the Support Vector Machine algorithm were used.
As a result of the Support Vector Machine algorithm, amount of foreign investors in the equity market, CDS spreads, government bonds interest rates, MSCI emerging markets index, and volatility index were determined as the most important variables on XU100 index in the pre-pandemic period. On the other hand, in pandemic-period, MSCI emerging markets index, the volatility index, retention amount of foreign investors in the equity market, amount of security hold by CBRT, and equity market traded value were the most important factors, respectively.
The results obtained in the study were similar to the other studies in the literature except for only one market variable which is the net buying amount of foreign investors. Although various researchers like Bekaert & Harvey (1995), Clark and Berko (1997), Choe et al. (1999), Tabak (2003), Dahlquist & Robertsson (2004), Akar (2008), Gümüş (2010), İskenderoğlu & Karadeniz (2011), Sevil et al. (2012), Vo (2015), Kesik et al. (2016), and Topaloğlu et al. (2019) defined that foreign investors' activities were important on stock exchange indices, we had interestingly reached opposite results for net buying amount of foreign investors variable in the study. In other words, the net buying amount of foreign investors did not affect the XU100 index in both pre-pandemic and pandemic periods.
The findings of the study mainly concluded that the effects and importance order of influential variables on the XU100 index varies according to the period whether Turkey is in the pre-pandemic or pandemic period. By considering this determination, the presence of COVID-19 currently and the results of the study, Turkey should focus on influential factors that are effective on the XU100 in the pandemic period. Therefore, Turkey should give priority to the most important variables firstly, and could deal with other factors after that. In this context, the main focus priorities of Turkey are the MSCI emerging markets index, volatility index, retention amount of foreign investors in the equity market, amount of security hold by CBRT, equity market traded value, USD/TL foreign exchange rates. Because MSCI emerging markets index and volatility index is global factors, they are not fully control of Turkey. For this reason, Turkey could give priority to decrease the negative effects of the amount of security hold by CBRT, equity market traded value, USD/TL foreign exchange rates variables on XU100 and stimulate the increase of retention amount of foreign investors in the equity market. Hence, Turkey could provide some earnings in supporting the increase of XU100 in total. After that, Turkey could focus on other factors in turn. In total, every precaution related to the decreasing country risk could be beneficial in providing a positive contribution to the variables used in the study and to XU100 in turn. Taking measures by considering the results of the study could help prevent the effects of the decrease of the influential variables on the XU100 index. By doing so negative effects could be prevented and assets traded in BIST could be priced at their fair value.
The results of the study emphasized the importance of the COVID-19 pandemic on the XU100 index that which factors are influential on XU100 index and importance of variables in terms of the significance vary according to period whether Turkey is in COVID-19 pandemic or not. Therefore, the most significant implication of analysis results for beneficiaries (especially for equity traders and investors) is that they should consider the development of COVID-19 in Turkey (i.e. probable second and third waves), and should allocate their portfolio assets among possible instruments by considering the effect of the pandemic on these alternatives. By considering that the effects of COVID-19 may change on alternatives, they should always follow up the development in financial markets as well. For example, MSCI announced that they will remove Turkey from MSCI emerging market index because of short sell ban in equity market. Therefore, equity traders should always consider such announcement in their decision-making process. Only after a while, Turkey has removed short sell ban from BIST 30 equities which are the most liquid indices in BIST. Also, this development should also be considered. As a summary, new announcements and developments may occur in every time and these may be either a positive or a negative leading indicator for main stock exchange indices as can be understood from this example. Equity traders and investors (individual & corporate) can re-arrange their portfolios by considering the analysis of the study. In this study, we focus on Turkey since the main stock exchange index of Turkey has decreased at a significant amount. Turkey could increase foreign portfolio investment inflows via equities. On the other hand, focusing on Turkey is the main limitation of the study. Also, focusing on macro-level factors is another limitation of the study. In future studies, other important indices in BIST like XU030 and XBANK could be examined and market-based examination could be performed. Moreover, the different bundle of developed and emerging countries like China (COVID-19 originated country), Hong Kong, India, Italy, Greece, Spain, Philippines, Brazil, South Africa which have an important amount of decreases in their national main stock exchanges in COVID-19 pandemic times could be examined in future studies for the extending literature. Moreover, new variables could be included in the analysis and new statistical or econometric methods could be applied in the forthcoming studies.
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
All authors declare no conflicts of interest in this paper.
| [1] | Adabag C, Ornelas JRH (2004) Behavior and Effects of Foreign Investors on Istanbul Stock Exchange. Available from: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=656442. |
| [2] | Akar C (2008) Yabancılar Türkiye'de Pozitif Geri Beslenme Hipotezine Uygun Davranışlar Gösterirler mi? İMKB Dergisi 10: 61-67. |
| [3] |
Alexander C, Kaeck A (2008) Regime Dependent Determinants of Credit Default Swap Spreads. J Bank Financ 32: 1008-1021. doi: 10.1016/j.jbankfin.2007.08.002
|
| [4] | Avcı ÖB (2015) Effect of Foreign Investor Transactions on Stock Market Returns. Hacettepe Üniversitesi İktisadi ve İdari Bilimler Fakültesi Dergisi 33: 29-38. |
| [5] | Baklacı HF (2007) Do Foreign Investors Chase or Impact Returns in Turkey? In: International Conference on Globalization and its Discontents, Cortland. |
| [6] | Baklacı HF (2008) İMKB'de Yabancı Yatırımcı Işlemleri ve Getiri Etkileşimi Üzerine Ampirik Bir Çalışma. İMKB Dergisi 11: 37-59. |
| [7] | Bekaert G, Harvey CR (1995) Emerging Equity Market Volatility. National Bureau of Economic Research, Working Paper, No. 5307. |
| [8] | Bekaert G, Harvey CR (1998) Capital Flows and the Behavior of Emerging Market Equity Returns. National Bureau of Economic Research, Working Paper, No. 6669. |
| [9] |
Bekaert G, Harvey CR (2003) Emerging Markets Finance. J Empir Financ 10: 3-55. doi: 10.1016/S0927-5398(02)00054-3
|
| [10] | BIST (2020a) About Borsa Istanbul. Available from: https://www.borsaistanbul.com/en/corporate/about-borsa-istanbul/milestones-in-borsa-istanbul-history, 07.11.2020. |
| [11] | BIST (2020b) Consolidated Data. Available from: https://www.borsaistanbul.com/en/data/data/consolidated-data, 07.11.2020. |
| [12] |
Boyer B, Zheng L (2009) Investor Flows and Stock Market Returns. J Empir Financ 16: 87-100. doi: 10.1016/j.jempfin.2008.06.003
|
| [13] | Breiman L (1996) Bagging Predictors. Mach Learn 24: 123-140. |
| [14] |
Breiman L (2001) Random Forests. Mach Learn 45: 5-32. doi: 10.1023/A:1010933404324
|
| [15] | CBRT (2020) Electronic Data Distribution System (EVDS). Available from: https://evds2.tcmb.gov.tr/index.php?/evds/serieMarket, 05.25.2020. |
| [16] | Choe H, Kho BC, Stulz RM (1999) Do Foreign Investors Destabilize Stock Markets? The Korean Experience in 1997. J Financ Econ 54: 227-264. |
| [17] | Clark J, Berko E (1997) Foreign Investment Fluctuations and Emerging Market Stock Returns: The Case of Mexico. FRB of New York, Staff Report, No. 24. |
| [18] |
Cremers KM, Driessen J, Maenhout P (2008) Explaining the Level of Credit Spreads: Option-Implied Jump Risk Premia in a Firm Value Model. Rev Financ Stud 21: 2209-2242. doi: 10.1093/rfs/hhn071
|
| [19] | CSD (2020) Data of Foreign Investors. Obtained from Central Securities Depositories of Turkey via e-mail on 05.25.2020. |
| [20] |
Dahlquist M, Robertsson G (2004) A Note on Foreigners' Trading and Price Effects across Firms. J Bank Financ 28: 615-632. doi: 10.1016/S0378-4266(03)00036-0
|
| [21] |
Demir C (2019) Macroeconomic Determinants of Stock Market Fluctuations: The Case of BIST-100. Economies 7: 8. doi: 10.3390/economies7010008
|
| [22] |
Dooley M, Hutchison M (2009) Transmission of the US Subprime Crisis to Emerging Markets: Evidence on the Decoupling-Recoupling Hypothesis. J Int Money Financ 28: 1331-1349. doi: 10.1016/j.jimonfin.2009.08.004
|
| [23] | Elmas B (2012) Yabancı Portföy Yatırımlarının İMKB'ye Etkisi: İMKB'de Endeks Bazlı Bir Çalışma. İMKB Dergisi 12: 1-18. |
| [24] | Erdoğan S, Gedikli A, Çevik Eİ (2019a) Volatility Spillover Effects between Islamic Stock Markets and Exchange Rates: Evidence from Three Emerging Countries. Borsa İstanbul Rev 2: 1-19. |
| [25] | Erdoğan S, Gedikli A, Çevik Eİ (2019b) The Impact of Macroeconomic Variables on Participation 30 Index in Turkey. Econometrics Lett 6: 25-34. |
| [26] |
Galil K, Shapir OM, Amiram D, et al. (2014) The Determinants of CDS Spreads. J Bank Financ 41: 271-282. doi: 10.1016/j.jbankfin.2013.12.005
|
| [27] |
Hajilee M, Al Nasser OM (2014) Exchange Rate Volatility and Stock Market Development in Emerging Economies. J Post Keynesian Econ 37: 163-180. doi: 10.2753/PKE0160-3477370110
|
| [28] | Hargis K, Ramanlal P (1997) The Internationalization of Emerging Equity Markets: Domestic Market Development or Market Retardation. Working Paper, University of South Carolina, Columbia, SC. Available from: https://ssrn.com/abstract=9502. |
| [29] | Hastie T, Tibshirani R, Friedman J (1996) The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2 Eds, Springer-Verlag. |
| [30] | İskenderoğlu Ö, Karadeniz E (2011) İMKB 100 Endeksi Getirisi ile Yabancı Portföy Yatırımları Arasındaki Ilişkinin Analizi. Çağ Üniversitesi Sosyal Bilimler Dergisi 8: 123-133. |
| [31] | Karikari JA (1992) Causality between Direct Foreign Investment and Economic Output in Ghana. J Econ Dev 17: 7-17. |
| [32] |
Kartal MT (2020) The Behavior of Sovereign Credit Default Swaps (CDS) Spread: Evidence from Turkey with the Effect of Covid-19 Pandemic. Quant Financ Econ 4: 489-502. doi: 10.3934/QFE.2020022
|
| [33] | Kesik A, Çanakcı M, Tunalı H (2016) Analyzing Impact of Non-Residents' Holdings of Equities on BIST (Istanbul Stock Exchange) 100 Index. J Econ Financ Accounting 3: 166-179. |
| [34] |
Kim W, Wei SJ (2002) Foreign Portfolio Investors Before and During a Crisis. J Int Econ 56: 77-96. doi: 10.1016/S0022-1996(01)00109-X
|
| [35] |
Kim EH, Singal V (2000) Stock Market Openings: Experience of Emerging Economies. J Bus 73: 25-66. doi: 10.1086/209631
|
| [36] | Gümüş GK (2010) Menkul Kıymet Piyasalarında Yabancı Yatırımcıların Etkisi: İstanbul Menkul Kıymetler Borsası Örneği. İMKB Dergisi 11: 61-96. |
| [37] |
Lahiani A, Hammoudeh S, Gupta R (2016) Linkages between Financial Sector CDS Spreads and Macroeconomic Influence in a Nonlinear Setting. Int Rev Econ Financ 43: 443-456. doi: 10.1016/j.iref.2016.01.007
|
| [38] |
Law T, Shawe-Taylor J (2017) Practical Bayesian Support Vector Regression for Financial Time Series Prediction and Market Condition Change Detection. Quant Financ 9: 1403-1416. doi: 10.1080/14697688.2016.1267868
|
| [39] |
Lee J, Chung KH (2018) Foreign Ownership and Stock Market Liquidity. Int Rev Econ Financ 54: 311-325. doi: 10.1016/j.iref.2017.10.007
|
| [40] |
Liew PX, Lim KP, Goh KL (2018) Foreign Equity Flows: Boon or Bane to the Liquidity of Malaysian Stock Market? North Am J Econ Financ 45: 161-181. doi: 10.1016/j.najef.2018.02.007
|
| [41] | McLean B, Shrestha S (2002) International Financial Liberalisation and Economic Growth. Reserve Bank of Australia, Research Discussion Paper, No. 3. |
| [42] | MHT (2020) COVID-19 Numbers. Available from: https://COVID19.saglik.gov.tr, 05.25.2020. |
| [43] | Morgan Stanley (2020) EEMEA COVID-19 Impact & Response. EEMEA Equity Strategy Research Report. Distributed by Morgan Stanley via email. |
| [44] | Naik PK, Padhi P (2014) An Empirical Evidence of Dynamic Interaction between Institutional Fund Flows and Stock Market Returns. MPRA Paper. Available from: https://mpra.ub.uni-muenchen.de/57723/. |
| [45] |
Nam D (2004) Do Foreign Investors Cause Noise in an Emerging Stock Market? J Emerg Mark Financ 3: 21-36. doi: 10.1177/097265270400300102
|
| [46] |
Naufa AM, Lantara IWN, Lau WY (2019) The Impact of Foreign Ownership on Return Volatility, Volume, and Stock Risks: Evidence from ASEAN Countries. Econ Anal Policy 64: 221-235. doi: 10.1016/j.eap.2019.09.002
|
| [47] | Official Gazette (2020) Available from: https://www.resmigazete.gov.tr. |
| [48] |
Orhan A, Kırıkkaleli D, Ayhan F (2019) Analysis of Wavelet Coherence: Service Sector Index and Economic Growth in an Emerging Market. Sustainability 11: 6684. doi: 10.3390/su11236684
|
| [49] | Sevil G, Özer M, Kulalı G (2012) Foreign Investors and Noise Trade in Istanbul Stock Exchange. Int J Bus Soc Scienc 3: 93-101. |
| [50] |
Shahzad SJH, Nor SM, Ferrer R, et al. (2017) Asymmetric Determinants of CDS Spreads: US Industry-Level Evidence through the NARDL Approach. Econ Model 60: 211-230. doi: 10.1016/j.econmod.2016.09.003
|
| [51] |
Shapire R, Freund Y, Bartlett P, et al. (1998) Boosting the Margin: A New Explanation for the Effectiveness of Voting Methods. Ann Stat 26: 1651-1686. doi: 10.1214/aos/1024691352
|
| [52] | Somuncu K, Karan MB (2005) The Impacts of International Portfolio Investments on Istanbul Stock Exchange Market. Turk Court Accounts 77: 149-167. |
| [53] |
Soumaré I, Tchana Tchana F (2015) Causality between FDI and Financial Market Development: Evidence from Emerging Markets. World Bank Econ Rev 29: 205-216. doi: 10.1093/wber/lhv015
|
| [54] |
Tabak BM (2003) The Random Walk Hypothesis and the Behaviour of Foreign Capital Portfolio Flows: The Brazilian Stock Market Case. Appl Financ Econ 13: 369-378. doi: 10.1080/09603100210134550
|
| [55] | Topaloğlu EE, Şahin S, Ege İ (2019) The Effect of Foreign Direct and Portfolio Investments on stock Market Returns in E7 Countries. J Accounting Financ, 263-278. |
| [56] | Vapnik VN (1995) The Nature of Statistical Learning Theory, Springer, New York. |
| [57] | Vapnik VN, Golowich S, Smola A (1996) Support Vector Method for Function Approximation, Regression Estimation and Signal Processing, In: Advances in Neural Information Processing Systems 9, MIT Press. |
| [58] | Vergil H, Karaca C (2010) The Effects of International Capital Movements through Developing Countries on Economic Growth: The Panel Data Analysis. Ege Acad Rev 10: 1207-1216. |
| [59] |
Vo XV (2015) Foreign Ownership and Stock Return Volatility-Evidence from Vietnam. J Multinatl Financ Manage 30: 101-109. doi: 10.1016/j.mulfin.2015.03.004
|
| [60] | WHO (2020) COVID-19 Numbers. Available from: https://COVID19.who.int, 05.25.2020. |
| [61] | Wiener M, Liaw A (2002) Classification and Regression by randomForest. R News 3: 18-22. |
| [62] |
Yang L, Yang L, Hamori S (2018) Determinants of Dependence Structures of Sovereign Credit Default Swap Spreads between G7 and BRICS Countries. Int Rev Financ Analy 59: 19-34. doi: 10.1016/j.irfa.2018.06.001
|
| [63] |
Zhang BY, Zhou H, Zhu H (2009) Explaining Credit Default Swap Spreads with the Equity Volatility and Jump Risks of Individual Firms. Rev Financ Stud 22: 5099-5131. doi: 10.1093/rfs/hhp004
|
| [64] | Zengin S, Yüksel S, Kartal MT (2018) Understanding the Factors that Affect Foreign Direct Investment in Turkey by Using MARS Method. J Financ Res Stud 10: 1309-1123. |
| 1. | Mustafa Tevfik Kartal, Serpil Kiliç Depren, Özer Depren, How Main Stock Exchange Indices React to Covid-19 Pandemic: Daily Evidence from East Asian Countries, 2021, 50, 1226-508X, 54, 10.1080/1226508X.2020.1869055 | |
| 2. | N.serap VURUR, BİST 100 ENDEKSİ CDS PRİMLERİ ARASINDAKİ İLİŞKİDE COVİD 19 ETKİSİ, 2021, 1307-9832, 10.18092/ulikidince.823358 | |
| 3. | Mustafa Tevfik KARTAL, Özer DEPREN, Serpil KILIÇ DEPREN, The relationship between mobility and COVID-19 pandemic: Daily evidence from an emerging country by causality analysis, 2021, 10, 25901982, 100366, 10.1016/j.trip.2021.100366 | |
| 4. | Zhifeng Liu, Toan Luu Duc Huynh, Peng-Fei Dai, The impact of COVID-19 on the stock market crash risk in China, 2021, 02755319, 101419, 10.1016/j.ribaf.2021.101419 | |
| 5. | Özgür Ömer ERSİN, Tuğçe ACAR, Özgür KIYAK, COVID-19 PANDEMİ DÖNEMİNDE VAKA SAYILARI, DÖVİZ KURU VE VIX ENDEKSİNİN GELİŞMEKTE OLAN PİYASALAR ÜZERİNDEKİ ETKİSİ: BİST 100 ENDEKSİ ÜZERİNE BİR ANALİZ, 2022, 1302-6739, 10.31671/doujournal.1016083 | |
| 6. | Leon Kohrt, Florian Horky, Jarko Fidrmuc, Exchange Rates in Emerging Markets in the First Wave of the Covid-19 Pandemic, 2022, 0012-8775, 1, 10.1080/00128775.2022.2074461 | |
| 7. | Ömer Faruk TAN, Hakan CAVLAK, Yasin CEBECİ, Necati GÜNEŞ, CAN HIGH DIVIDEND YIELD SUSTAIN FIRM VALUE DURING THE COVID-19 CRASH? EVIDENCE FROM TURKISH FIRMS, 2021, 2148-029X, 10.11611/yead.915018 | |
| 8. | Mustafa Tevfik Kartal, The role of consumption of energy, fossil sources, nuclear energy, and renewable energy on environmental degradation in top-five carbon producing countries, 2022, 184, 09601481, 871, 10.1016/j.renene.2021.12.022 | |
| 9. | Sawssan Saadaoui, Mohamed Benmeriem, Hanane Abdelli, Zouheyr Gheraia, How Did Covid 19 Affect Strategic Goods? A Study Using the Scenario Method, 2022, 18, 2224-3496, 944, 10.37394/232015.2022.18.90 | |
| 10. | Mustafa Tevfik Kartal, Fatih Ayhan, Derviş Kirikkaleli, Regime-switching effect of COVID-19 pandemic on stock market index: evidence from Turkey as an emerging market example, 2022, 1752-0843, 1, 10.1080/17520843.2022.2091825 | |
| 11. | Mustafa Tevfik Kartal, Mustafa Kevser, Fatih Ayhan, Asymmetric effects of global factors on return of cryptocurrencies by novel nonlinear quantile approaches, 2023, 1573-9414, 10.1007/s10644-023-09484-x | |
| 12. | Mustafa Tevfik Kartal, Serpil Kılıç Depren, Özer Depren, Housing prices in emerging countries during COVID-19: evidence from Turkey, 2021, 1753-8270, 10.1108/IJHMA-07-2021-0083 | |
| 13. | Hasan Murat Ertuğrul, Mustafa Tevfik Kartal, Serpil Kılıç Depren, Uğur Soytaş, Determinants of Electricity Prices in Turkey: An Application of Machine Learning and Time Series Models, 2022, 15, 1996-1073, 7512, 10.3390/en15207512 | |
| 14. | Hakan Altin, 2022, chapter 5, 9781799869009, 106, 10.4018/978-1-7998-6900-9.ch005 | |
| 15. | Gamze GÖÇMEN YAĞCILAR, Borsa İstanbul’da COVID-19 Etkisi: Kısa Dönemli Sektörel Piyasa Tepkilerinin Endeks Bazında Ölçülmesi, 2021, 2587-151X, 439, 10.30784/epfad.865285 | |
| 16. | Mustafa Tevfik Kartal, The Effect of the COVID-19 Pandemic on Oil Prices: Evidence From Turkey, 2021, 1, 2652-6433, 10.46557/001c.18723 | |
| 17. | Mehmet Kiziloglu, Oleksandr Dluhopolskyi, Jan Laskowski, Agnieszka Laskowska, Creating Agile Institutions with Organizational Trust in the Finance Sector of Turkey: The Mediating Role of Psychological Empowerment in Times of COVID-19, 2023, 15, 2071-1050, 3019, 10.3390/su15043019 | |
| 18. | Mustafa Tevfik Kartal, Hasan Murat Ertuğrul, Talat Ulussever, The impacts of foreign portfolio flows and monetary policy responses on stock markets by considering COVID-19 pandemic: Evidence from Turkey, 2022, 22, 22148450, 12, 10.1016/j.bir.2021.06.003 | |
| 19. | Serpil Kılıç Depren, Mustafa Tevfik Kartal, Hasan Murat Ertuğrul, Özer Depren, The role of data frequency and method selection in electricity price estimation: Comparative evidence from Turkey in pre-pandemic and pandemic periods, 2022, 186, 09601481, 217, 10.1016/j.renene.2021.12.136 | |
| 20. | Jinyu Chen, Yilin Wang, Xiaohang Ren, Asymmetric effects of non-ferrous metal price shocks on clean energy stocks: Evidence from a quantile-on-quantile method, 2022, 78, 03014207, 102796, 10.1016/j.resourpol.2022.102796 | |
| 21. | Mustafa Tevfik KARTAL, Özer DEPREN, Serpil KILIÇ DEPREN, Do Monetary Policy Measures Affect Foreign Exchange Rates during the COVID-19 Pandemic? Evidence from Turkey, 2021, 1307-5705, 175, 10.46520/bddkdergisi.987416 | |
| 22. | Fatih Ayhan, Mustafa Tevfik Kartal, Tomiwa Sunday Adebayo, Derviş Kirikkaleli, Nexus between economic risk and political risk in the United Kingdom: Evidence from wavelet coherence and quantile‐on‐quantile approaches, 2022, 0307-3378, 10.1111/boer.12371 | |
| 23. | Özer Depren, Mustafa Tevfik Kartal, Serpil Kılıç Depren, Changes of gold prices in COVID-19 pandemic: Daily evidence from Turkey's monetary policy measures with selected determinants, 2021, 170, 00401625, 120884, 10.1016/j.techfore.2021.120884 | |
| 24. | Mustafa Tevfik Kartal, Özer Depren, Serpil Kilic Depren, Do Monetary Policy Measures Affect Foreign Exchange Rates during the COVID-19 Pandemic? Evidence from Turkey, 2021, 1556-5068, 10.2139/ssrn.3915756 | |
| 25. | Tomiwa Sunday Adebayo, Mustafa Tevfik Kartal, Effect of green bonds, oil prices, and COVID-19 on industrial CO2 emissions in the USA: Evidence from novel wavelet local multiple correlation approach, 2023, 0958-305X, 0958305X2311674, 10.1177/0958305X231167463 | |
| 26. | Ömer Faruk TAN, The Impact of News about Pandemic on Borsa Istanbul during the COVID-19 Financial Turmoil, 2021, 2630-6220, 109, 10.17829/turcom.859299 | |
| 27. | Hossain Mohammad Reyad, Momtaj Ayesha, Mohammed Masum Iqbal, Mohd Ashhari Zariyawati, The role of ESG in enhancing firm resilience to geopolitical risks: An eastern European perspective, 2024, 7, 2572-3170, 10.1002/bsd2.70027 | |
| 28. | Mustafa Tevfik Kartal, Ugur Korkut Pata, Dilvin Taşkın, Talat Ulussever, Relationship between monetary policy and financial asset returns in Türkiye: Time, frequency, and quantile-based effects, 2024, 24, 22148450, 474, 10.1016/j.bir.2024.02.005 | |
| 29. | Ahmed Alsayed, Kivanç Ariç, Siok Sek, The behavior of stock market index during the coronavirus pandemic in Turkey, 2024, 71, 1452-595X, 555, 10.2298/PAN211123001A | |
| 30. | Aydın Gürbüz, BIST 100 ve Katılım 50 Endekslerinin Döviz Kuru, CDS Risk Primi, CBOE Oynaklık Endeksi (VIX) ve Petrol Fiyatları Arasındaki İlişkinin İncelenmesi, 2024, 21, 1304-8120, 769, 10.33437/ksusbd.1400787 | |
| 31. | Mustafa Tevfik Kartal, Serpil Kılıç Depren, Ugur Korkut Pata, Dilvin Taşkın, Tuba Şavlı, Modeling the link between environmental, social, and governance disclosures and scores: the case of publicly traded companies in the Borsa Istanbul Sustainability Index, 2024, 10, 2199-4730, 10.1186/s40854-024-00619-1 | |
| 32. | Sihyun An, Jihae Kim, Gahyun Choi, Hanwool Jang, Kwangwon Ahn, The effect of rare events on information-leading role: evidence from real estate investment trusts and overall stock markets, 2024, 11, 2662-9992, 10.1057/s41599-024-04146-3 |
Mustafa Tevfik Kartal, Özer Depren, Serpil Kılıç Depren. The determinants of main stock exchange index changes in emerging countries: evidence from Turkey in COVID-19 pandemic age[J]. Quantitative Finance and Economics, 2020, 4(4): 526-541. doi: 10.3934/QFE.2020025
| Group | Variable | Symbol | Description | Effect | Data |
| Dependent | BIST Main Index | XU100 | Trading Day Closing Value of XU100 | N/A | Bloomberg |
| Global | MSCI Emerging Market Index | MXEF | MSCI Emerging Market Index | + | Bloomberg |
| Volatility Index | VIX | Chicago Board Options Exchange Volatility Index | - | Bloomberg | |
| Oil Prices | OIL | Crude Oil Prices (TL) | - | Bloomberg | |
| Country Level | CDS Spreads | CDS | 5-Years Sovereign CDS Spreads of Turkey | - | Bloomberg |
| Treasury Bond Interest Rates | DIBS | 1-Year Treasury Bond Interest Rate of Turkey (%) | - | Bloomberg | |
| USD/TL FER | USDTL | USD/TL Foreign Exchange Rate | - | CBRT | |
| TL Reference Interest Rate | TLREF | Daily TL Reference Interest Rate (%) | - | CBRT | |
| CBRT Net Funding Amount | CBRT_FUND | Net Funding Amount to Market Provided by CBRT | + | CBRT | |
| CBRT Securities Amount | CBRT_SEC | Net Amount of Securities Held by CBRT | + | CBRT | |
| Market | Equity Market Traded Value | EMVOL | Daily Equity Market Traded Value | + | Bloomberg |
| Foreign Investors' Share in Traded Value | ISHARE | Share of Foreign Investors in Traded Value | + | CSD | |
| Foreign Investors' Share in Retention | FSHARE | Equity Retention Rate of Foreign Investors | + | CSD | |
| Retention Amount of Foreign Investors in Equity Market | FAMOUNT | Retention Amount of Foreign Investors in Equity Market | + | CSD | |
| Foreign Investors' Net Buying Amount | NETBUY | Net Buying Amount of Foreign Investors | + | CSD | |
| COVID-19 | COVID-19 Presence | CVD | 1: If COVID-19 exists; 0: otherwise | - | MHT |
| Note: N/A means that not applicable since this is dependent variable. Positive (+) relationship means that XU100 increases when independent variables increase. Negative (-) relationship means that XU100 decreases when independent variables increase. |
|||||
DownLoad:
CSV
| Pre-Pandemic Period | Pandemic Period | Independent Sample t-test | |||||
| Mean | SD | Mean | SD | Sig. (2-tailed) | |||
| XU100 | 117.362 | 4.932 | 94.743 | 5.272 | 0.000 | ||
| MXEF | 1.090.6 | 43.7 | 872.8 | 44.0 | 0.000 | ||
| VIX | 19.4 | 10.2 | 47.4 | 14.7 | 0.000 | ||
| OIL | 349.4 | 36.1 | 168.1 | 25.5 | 0.000 | ||
| CDS | 280.2 | 43.5 | 577.9 | 62.4 | 0.000 | ||
| DIBS | 11.1 | 0.8 | 10.1 | 1.4 | 0.000 | ||
| TLREF | 11.1 | 0.5 | 9.3 | 0.8 | 0.000 | ||
| USDTL | 6.0 | 0.1 | 6.7 | 0.3 | 0.000 | ||
| CBRT FUND | 6.348 | 3.793 | 16.870 | 3.608 | 0.000 | ||
| CBRT SEC | 3.225 | 100 | 5.944 | 2.332 | 0.000 | ||
| EMVOL | 3.006 | 583 | 2.367 | 516 | 0.000 | ||
| ISHARE | 24.8 | 3.2 | 20.7 | 5.3 | 0.000 | ||
| FSHARE | 0.61 | 0.02 | 0.59 | 0.02 | 0.000 | ||
| FAMOUNT | 49.678 | 4.826 | 35.435 | 2.388 | 0.000 | ||
| NETBUY | -35.8 | 54.0 | -48.3 | 30.9 | 0.173 | ||
| SD: Standard Deviation. | |||||||
DownLoad:
CSV
| Pre-Pandemic Period | Pandemic Period | ||||||
| Methods | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| Support Vector Machine | 94.3% | 1216.28 | 992.34 | 96.8% | 1021.78 | 749.80 | |
| Random Forest | 93.6% | 1478.50 | 1131.91 | 95.8% | 1163.57 | 908.61 | |
DownLoad:
CSV
| Group | Variable | Symbol | Description | Effect | Data |
| Dependent | BIST Main Index | XU100 | Trading Day Closing Value of XU100 | N/A | Bloomberg |
| Global | MSCI Emerging Market Index | MXEF | MSCI Emerging Market Index | + | Bloomberg |
| Volatility Index | VIX | Chicago Board Options Exchange Volatility Index | - | Bloomberg | |
| Oil Prices | OIL | Crude Oil Prices (TL) | - | Bloomberg | |
| Country Level | CDS Spreads | CDS | 5-Years Sovereign CDS Spreads of Turkey | - | Bloomberg |
| Treasury Bond Interest Rates | DIBS | 1-Year Treasury Bond Interest Rate of Turkey (%) | - | Bloomberg | |
| USD/TL FER | USDTL | USD/TL Foreign Exchange Rate | - | CBRT | |
| TL Reference Interest Rate | TLREF | Daily TL Reference Interest Rate (%) | - | CBRT | |
| CBRT Net Funding Amount | CBRT_FUND | Net Funding Amount to Market Provided by CBRT | + | CBRT | |
| CBRT Securities Amount | CBRT_SEC | Net Amount of Securities Held by CBRT | + | CBRT | |
| Market | Equity Market Traded Value | EMVOL | Daily Equity Market Traded Value | + | Bloomberg |
| Foreign Investors' Share in Traded Value | ISHARE | Share of Foreign Investors in Traded Value | + | CSD | |
| Foreign Investors' Share in Retention | FSHARE | Equity Retention Rate of Foreign Investors | + | CSD | |
| Retention Amount of Foreign Investors in Equity Market | FAMOUNT | Retention Amount of Foreign Investors in Equity Market | + | CSD | |
| Foreign Investors' Net Buying Amount | NETBUY | Net Buying Amount of Foreign Investors | + | CSD | |
| COVID-19 | COVID-19 Presence | CVD | 1: If COVID-19 exists; 0: otherwise | - | MHT |
| Note: N/A means that not applicable since this is dependent variable. Positive (+) relationship means that XU100 increases when independent variables increase. Negative (-) relationship means that XU100 decreases when independent variables increase. |
|||||
| Pre-Pandemic Period | Pandemic Period | Independent Sample t-test | |||||
| Mean | SD | Mean | SD | Sig. (2-tailed) | |||
| XU100 | 117.362 | 4.932 | 94.743 | 5.272 | 0.000 | ||
| MXEF | 1.090.6 | 43.7 | 872.8 | 44.0 | 0.000 | ||
| VIX | 19.4 | 10.2 | 47.4 | 14.7 | 0.000 | ||
| OIL | 349.4 | 36.1 | 168.1 | 25.5 | 0.000 | ||
| CDS | 280.2 | 43.5 | 577.9 | 62.4 | 0.000 | ||
| DIBS | 11.1 | 0.8 | 10.1 | 1.4 | 0.000 | ||
| TLREF | 11.1 | 0.5 | 9.3 | 0.8 | 0.000 | ||
| USDTL | 6.0 | 0.1 | 6.7 | 0.3 | 0.000 | ||
| CBRT FUND | 6.348 | 3.793 | 16.870 | 3.608 | 0.000 | ||
| CBRT SEC | 3.225 | 100 | 5.944 | 2.332 | 0.000 | ||
| EMVOL | 3.006 | 583 | 2.367 | 516 | 0.000 | ||
| ISHARE | 24.8 | 3.2 | 20.7 | 5.3 | 0.000 | ||
| FSHARE | 0.61 | 0.02 | 0.59 | 0.02 | 0.000 | ||
| FAMOUNT | 49.678 | 4.826 | 35.435 | 2.388 | 0.000 | ||
| NETBUY | -35.8 | 54.0 | -48.3 | 30.9 | 0.173 | ||
| SD: Standard Deviation. | |||||||
| Pre-Pandemic Period | Pandemic Period | ||||||
| Methods | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| Support Vector Machine | 94.3% | 1216.28 | 992.34 | 96.8% | 1021.78 | 749.80 | |
| Random Forest | 93.6% | 1478.50 | 1131.91 | 95.8% | 1163.57 | 908.61 | |
