1. Introduction

The theory of real business cycle and Keyneianism IS-LM model (Kynes J M, 1936) are two frameworks in macroeconomics which are both widely approved. Although the two theories are very different, they both follow Modigliani-Miller theorem, which says that financial factors make no difference to real economic variables. However, after American subprime mortgage crisis, the effects of financial factors on business cycle are becoming more remarkable (Alpanda S et al., 2014; Christiano L et al., 2007; Jerman U et al., 2012), which form the features of financial business cycle (Iacoviello M, 2015; Mimir Y, 2016). Firstly, the economy and financial factors have intimate connections (Claessens S et al., 2012). Secondly, the economy fluctuates continuously by shocks which are transmitted by monetary sector (Kamber G et al., 2013; Kollmann R, 2013). Thirdly, tiny change may be magnified by financial market such that it could lead to a big shock hitting on global economy (Luca D et al., 2009). These features have exceeded the research scope of classical theories of business cycle. It raises the need of a framework for analysis. Many economists and mathematical finance scholars have attempted to introduce financial factors into the frameworks of business cycle.

Under the framework of Keyneianism, both the well known Kaldor and Kalecki business cycle models use an investment function which is based on the profit principle rather than the acceleration principle. In the Kaldor (1940) model, the gross investment depends on the level of output and capital stock. For a given quantity of real capital, investment depends on the level of profit, which in turns depends on the level of activity. Kaldor presented the assumptions on nonlinear investment and savings function and their shift over time which give rise to a cycle. Thereafter, the model has been paid much attentions. Varian (1979) explored the possibility that the economic system possesses a unique limit cycle. The most important result was the paper (Chang W et al., 1971), where the model was reexamined and the necessary and sufficient conditions of the existence of a limit cycle were stated. The coexistence of a limit cycle and an equilibrium was considered by Grasman and Wentzel (1994). The Kalecki (1935, 1937) business cycle model was a few years earlier than the Kaldor one. Kalecki assumed that the saved part of profit is invested and the capital growth is due to past investment decisions. There is a gestation period or a time lag, after which capital equipment is available for production. Krawiec and Szydłwsk (1999, 2001) formulated the Kaldor-Kalecki business cycle model based on the multiplier dynamics which is the core of both the Kaldor and Kalecki's approach but followed Kalecki's idea to investment and of a time lag between investment decisions and implementation. They obtained a delay differential equation system and applied the Hopf bifurcation mechanism to create the limit cycle. They showed that the dynamics of the system depended crucially on the time delay parameter. Then they investigated the stability of the limit cycle (Szydłwsk M et al., 2005). Following the works of Krawiec and Szydłwsk, Kaddar and Alaoui (2008, 2009) proposed another delay Kaldor-Kalecki model of business cycle. They derived the similar results to those of Krawiec and Szydłwsk (1999, 2001). More other results about the Kaldor-Kalecki model can be referred to Bashkirtseva et al. (2016), De Cesare et al. (2012), Liao et al. (2005), Mircea et al. (2011), Wang et al. (2009), Wu (2012), Zhang et al. (2004). For example, Liao et al. (2005) studied chaos in the model. Wu (2012) carried out the zero-Hopf bifurcation of the model. Bashkirtseva et al. (2016) analyzed the stochastic effects in the discrete Kaldor-Kalecki model. Mircea et al. (2011) studied the Hopf bifurcation of the mean and variance of a stochastic Kaldor-Kalecki model.

The aim of this paper is to model business cycle under shocks and see the effects of shocks on the economic system. We introduce the financial shocks into the Kaldor-Kalecki model. The financial shocks are regarded as random noises perturbing the model and thus the model shows volatility and risky. Then we study the dynamics of the model in the framework of stochastic differential equations (Øksendal B et al., 2000) and random dynamical systems (Arnold L, 1988; Crauel H et al., 1999), which can help us understand the effects of financial shocks on business cycle and improve our knowledge of the law of financial business cycle. As we focus on the effects of financial shocks on the model, we omit the time-delay effect in the Kaldor-Kalecki model.

The paper is organized as follows. In Section 2, we simplify the Kaldor-Kalecki model into a normal form in the framework of ordinary differential equations. The normal form of the Kaldor-Kalecki model admits the same essence as the original Kaldor-Kalecki model, but just is more convenient to consider. Then by applying the polar transformation, the model is transferred into a more intuitionistic form and the existence of limit cycle, which implies the business cycle, is proved. In Section 3, we introduce shocks, which are regarded as noises, into the normalized Kaldor-Kalecki model and make it stochastic. The shocks include external shock and internal shock. Then the dynamics of the stochastic models with external shock, internal shock, both external shock and internal shock are investigated respectively in the framework of stochastic differential equations and random dynamical systems. We present conditions of intensities of shocks under which the system shows different kinds of dynamics, such as behaving randomly periodically, converging to normalcy, behaving uncertainly and disorderly. Especially, production of stable invariant measure of the random dynamical system associating with the stochastic model means that the system behaves randomly periodically, namely that the amplitude and velocity of period are random but stationary, whose laws are invariant with respect to time. In Section 4, we give some discussions about the effects of financial shocks on the economic system.

---

2. Kaldor-Kalecki Model

In this section, we simplify the Kaldor-Kalecki model to a normal form and prove the existence of limit cycle. The Kaldor macro business cycle model (Kaddar A et al., 2008) is a two-dimensional autonomous dynamical system in the form

$\left\{ \begin{split} &Y'=\alpha(I(Y,K)-S(Y,K)),\\ &K'=I(Y,K)-q K, \end{split} \right.$

(2.1)

where $I$ is the nonlinear investment and $S$ is the savings function, $Y$ is gross product, $K$ is capital stock, $\alpha$ is the adjustment coefficient in the goods market, and $q$ is the depreciation rate of the capital stock. Similar to Kaddar's assumption (2008), we assume that the savings function $S$ depends only on $Y$ and is linear such that $S (Y)=\gamma Y$, $\gamma > 0$. The investment function separates with respect to its two arguments and is linear with respect to $K$, that is $I (Y, K)=I (Y)-\beta K$, $\beta > 0$. Then system (2.1) translates to the following differential equations

$\left\{ \begin{split} &Y'=\alpha I(Y)-\alpha\beta K-\alpha\gamma Y,\\ &K'=I(Y)-(\beta+q)K. \end{split} \right.$

(2.2)

It is easy to see that there is a non-trivial steady state $(Y^{*}, K^{*})$ such that

$\left\{ \begin{split} &I(Y^{*})-\beta K^{*}-\gamma Y^{*}=0,\\ &I(Y^{*})-(\beta+q)K^{*}=0. \end{split} \right.$

(2.3)

Making a transformation of coordinates $y=Y-Y^{*}$, $k=K-K^{*}$, the system is translated into

$\left\{ \begin{split} &y'=\alpha(i(y)-\beta k-\gamma y),\\ &k'=i(y)-(\beta+q)k, \end{split} \right.$

(2.4)

where $i (y)=I (y+Y^{*})-I (Y^{*})$, which is similar to system (2.1) formally. Hence, without loss of generality, it is reasonable and convenient to consider $(0, 0)$ as the steady state which we will work on.

---

2.1. Normal Form of Kaldor-Kalecki Model

In this subsection, we carry out a normal form of the Kaldor-Kalecki model, which is a simplification without loosing essential information of the system. Suppose that $I$ is a sufficiently smooth function. Expanding $I$ at $0$, system (2.2) is approximately translated into the following form:

$\left\{ \begin{split} Y'=&(\alpha I'(0)-\alpha\gamma)Y-\alpha\beta K+\frac{\alpha}{2}I''(0)Y^{2}+\frac{\alpha}{6}I'''(0)Y^{3}+O(Y^{4}),\\ K'=&I'(0)Y-(\beta+q)K+\frac{1}{2}I''(0)Y^{2}+\frac{1}{6}I'''(0)Y^{3}+O(Y^{4}). \end{split} \right.$

(2.5)

The eigenpolynomial of the system is given by

$\lambda^{2}+(\alpha\gamma+\beta+q-\alpha I'(0))\lambda+\alpha\beta\gamma+\alpha\gamma q-\alpha qI'(0)=0.$

(2.6)

Supposing that $\lambda=\lambda_{r}\pm\lambda_{c}\mathbf{i}$ are foots of (2.6), then $\lambda_{r}$ is solved by

$\lambda_{r}=\frac{1}{2}(\alpha I'(0)-\alpha\gamma-\beta-q).$

(2.7)

Supposing that

$(\alpha\gamma+\beta+q-\alpha I'(0))^{2}-4\alpha\beta\gamma-4\alpha\gamma q+4\alpha qI'(0)<0,$

(2.8)

then

$\lambda_{c}=\frac{1}{2}\sqrt{4\alpha\beta\gamma+4\alpha\gamma q-4\alpha qI'(0)-(\alpha\gamma+\beta+q-\alpha I'(0))^{2}}.$

(2.9)

Making the transformation of coordinates

$\left\{ \begin{split} &\phi=(-\beta-q-\lambda_{r})Y+\alpha\beta K,\\ &\varphi=\lambda_{c} Y, \end{split} \right.$

(2.10)

then system (2.5) is translated into the following form:

$\left\{ \begin{split} \varphi'=&\lambda_{r}\varphi-\lambda_{c}\phi+\frac{\alpha}{2\lambda_{c}}I''(0)\varphi^{2}+\frac{\alpha}{6\lambda_{c}^{2}}I'''(0)\varphi^{3},\\ \phi'=&\lambda_{r}\phi+\lambda_{c}\varphi+\frac{\alpha(-q-\lambda_{r})}{2\lambda_{c}^{2}}I''(0)\varphi^{2}+\frac{\alpha(-q-\lambda_{r})}{6\lambda_{c}^{3}}I'''(0)\varphi^{3}, \end{split} \right.$

(2.11)

where we omit the high order terms. In the framework of normal form of ordinary differential equations, the system can be simplified into the following form:

$\left\{ \begin{split} &\varphi'=\lambda_{r}\varphi-\lambda_{c}\phi+(\nu\varphi-\kappa\phi)(\varphi^{2}+\phi^{2}),\\ &\phi'=\lambda_{c}\varphi+\lambda_{r}\phi+(\kappa\varphi+\nu\phi)(\varphi^{2}+\phi^{2}),\\ \end{split} \right.$

(2.12)

where

$\nu=\frac{\alpha I'''(0)}{16\lambda_{c}^{2}}+\frac{\alpha^{2}I''^{2}(0)}{8|\lambda|^{2}\lambda_{c}^{2}}\bigg(-2q-\lambda_{r}-\frac{(q+\lambda_{r})^{2}\lambda_{r}}{\lambda_{c}^{2}}\bigg)$

(2.13)

and

$\kappa=-\frac{\alpha(q+\lambda_{r})I'''(0)}{16\lambda^{3}_{c}}+\frac{\alpha^{2}I''^{2}(0)}{4|\lambda|^{2}\lambda_{c}}\bigg(-\frac{(q+\lambda_{r})\lambda_{r}}{\lambda_{c}^{2}}+\frac{(q+\lambda_{r})^{2}}{2\lambda_{c}^{2}}-\frac{1}{2}\bigg).$

(2.14)

The detailed procedure of simplification can be found in Appendix A.

---

2.2. Existence of Limited Cycle

Making the transformation of polar coordinates $\varphi=r\cos\Theta$, $\phi=r\sin\Theta$, then we have

$\left\{ \begin{split} &r'=\lambda_{r}r+\nu r^{3},\\ &\Theta'=\lambda_{c}+\kappa r^{2}. \end{split} \right.$

(2.15)

If $\lambda_{r} < 0$, $\nu > 0$ or $\lambda_{r} > 0$, $\nu < 0$, letting $\lambda_{r}r+\nu r^{3}=0$, one can get $r=0$, $r=\pm\sqrt{-\frac{\lambda_{r}}{\nu}}$. Hence, $r=\sqrt{-\frac{\lambda_{r}}{\nu}}$ is a limited cycle.

Case Ⅰ. $\lambda_{r} > 0$, $\nu < 0$. As $r < \sqrt{-\frac{\lambda_{r}}{\nu}}$, $r' > 0$. As $r > \sqrt{-\frac{\lambda_{r}}{\nu}}$, $r' < 0$. Hence, $r=\sqrt{-\frac{\lambda_{r}}{\nu}}$ is a stable limited cycle.

Case Ⅱ. $\lambda_{r} < 0$, $\nu > 0$. As $r < \sqrt{-\frac{\lambda_{r}}{\nu}}$, $r' < 0$. As $r > \sqrt{-\frac{\lambda_{r}}{\nu}}$, $r' > 0$. Hence, $r=\sqrt{-\frac{\lambda_{r}}{\nu}}$ is a unstable limited cycle.

The period of the business cycle is given by

$T=\frac{2\pi\nu}{\nu\lambda_{c}-\kappa\lambda_{r}}.$

(2.16)

---

3. Stochastic Dynamics Driven by Financial Shocks

In Section 2, we have obtained a normal form (2.12) of the original system (2.5) and proved the existence of business cycle as long as the parameters satisfy $\lambda_{r} < 0$, $\nu > 0$ or $\lambda_{r} > 0$, $\nu < 0$. In the first case, the limited cycle is unstable. In the second case, the limited cycle is stable. Recalling that the aim of this paper is investigating the effects of financial shocks making on the economic system, in this section, we introduce the financial shocks into system (2.15), which is equivalent to system (2.12). The financial shocks are expressed as noises. Through out of this section, we assume that $\lambda_{r} > 0$, $\nu < 0$.

---

3.1. Stochastic Model with External Shock

In this subsection, we introduce the financial shock into system (2.15) and get the following stochastic system

$\left\{ \begin{split} &r'=\lambda_{r}r+\nu r^{3}+\epsilon r\xi_{t},\\ &\Theta'=\lambda_{c}+\kappa r^{2}, \end{split} \right.$

(3.1)

where $\xi_{t}$ is a white noise. Note that the original equivalent solution $r=\sqrt{-\frac{\lambda_{r}}{\nu}}$ was destroyed by the noise. Hence, the noise can be interpreted as external shock (Øksendal B et al, 2001). In the following argument, we study the dynamics of system (3.1) in the framework of stochastic differential equations of ItÔ type and random dynamical system. We choose ItÔ interpretation and rewrite system (3.1) as

$\left\{ \begin{split} &dr=(\lambda_{r}r+\nu r^{3})dt+\epsilon rdB(t),\\ &d\Theta=(\lambda_{c}+\kappa r^{2})dt, \end{split} \right.$

(3.2)

where $B (t)$ is a Brownian motion defined on a probability space $(\Omega, \mathcal{F}, \{\mathcal{F}_{t}\}_{t\geq0}, \mathbb{P})$. Denote $\{\theta_{t}\}_{t\in\mathbb{R}}$ the classical Brownian shift on the probability space. According to the results given by Arnold (1998), there exists a unique local random dynamical system $\Phi$ such that $(\Phi (t, \cdot) r_{0})_{t\in\mathbb{R}}$ is the unique maximal strong solution of (3.2) with initial value $r_{0}\geq0$. It is represented by

$\Phi(t,\omega)r_{0}=r_{0}+\int_{0}^{t}(\lambda_{r}\Phi(s,\omega)r_{0}+\nu\Phi^{3}(s,\omega)r_{0})ds+\epsilon\int_{0}^{t}\Phi(s,\omega)r_{0}dB(s)$

(3.3)

for $t\in (\tau^{-}(r_{0}, \omega), \tau^{+}(r_{0}, \omega))$, where $\tau^{+}$ and $\tau^{-}$ are the forward and backward explosion times of the orbit $\Phi (\cdot, \omega) r_{0}$ starting at time $t=0$ in position $r_{0}$. In the framework of stochastic bifurcation of random dynamical system, we have the following results:

Proposition 3.1. System (3.3) undergoes a stochastic pitchfork bifurcation at $\lambda_{r}=\frac{\epsilon^{2}}{2}$, and undergoes a P-bifurcation at $\lambda_{r}=\epsilon^{2}$. The generated non-trivial invariant measure supported on $\mathbb{R}^{+}$ is denoted by $\delta_{r_{+}}$, where

$r_{+}=\bigg(-2\nu\int_{-\infty}^{0}\exp(2\lambda_{r}s-\epsilon^{2}s+2\epsilon B(s))ds\bigg)^{-\frac{1}{2}},$

(3.4)

whose probability density function is given as

$p^{+}(r)=2\bigg(-\frac{\epsilon^{2}}{\nu}\bigg)^{\frac{1}{2}-\frac{\lambda_{r}}{\epsilon^{2}}}\Gamma^{-1}\bigg(\frac{\lambda_{r}}{\epsilon^{2}}-\frac{1}{2}\bigg)r^{(2\lambda_{r}-2\epsilon^{2})/\epsilon^{2}}e^{\frac{\nu}{\epsilon^{2}} r^{2}}.$

(3.5)

The proof of Proposition 3.1 can be found in Appendix B. Returning to system (3.2), we have

$\left\{ \begin{split} r_{+}(\theta_{t}\omega)=&\exp\bigg(\lambda_{r} t-\frac{\epsilon^{2}}{2}t+\epsilon B(t)\bigg)/\bigg(-2\nu\int_{-\infty}^{t}\exp(2\lambda_{r}s-\epsilon^{2}s+2\epsilon B(s))ds\bigg)^{\frac{1}{2}},\\ \Theta(t)=&\Theta_{0}+\lambda_{c}t+\kappa\int_{0}^{t}r^{2}_{+}(\theta_{s}\omega)ds. \end{split} \right.$

(3.6)

As $r_{+}$ is a ergodic and stationary process, it can be regarded as a stochastic limited cycle of system (3.2), corresponding to the deterministic limited cycle of system (2.15). The mean of amplitude $r_{+}$ can be calculated as

$\begin{split} \mathbb{E}[r_{+}]=\int_{0}^{\infty}rp^{+}(r)dr=\sqrt{-\frac{\epsilon^{2}}{\nu}}\Gamma\bigg(\frac{\lambda_{r}}{\epsilon^{2}}\bigg)\Gamma^{-1}\bigg(\frac{\lambda_{r}}{\epsilon^{2}}-\frac{1}{2}\bigg). \end{split}$

(3.7)

The mean of $r_{+}^{2}$ can be calculated as

$\begin{split} \mathbb{E}^{+}[r_{+}^{2}]=\int_{0}^{\infty}r^{2}p^{+}(r)dr=-\frac{\epsilon^{2}}{\nu}\Gamma\bigg(\frac{\lambda_{r}}{\epsilon^{2}}+\frac{1}{2}\bigg)\Gamma^{-1}\bigg(\frac{\lambda_{r}}{\epsilon^{2}}-\frac{1}{2}\bigg), \end{split}$

(3.8)

which implies the mean of the rate $\Theta'(t)$ can be given as

$\mathbb{E}[\Theta'(t)]=\lambda_{c}+\kappa\mathbb{E}[r^{2}_{+}]=\lambda_{c}-\frac{\kappa\epsilon^{2}}{\nu}\Gamma\bigg(\frac{\lambda_{r}}{\epsilon^{2}}+\frac{1}{2}\bigg)\Gamma^{-1}\bigg(\frac{\lambda_{r}}{\epsilon^{2}}-\frac{1}{2}\bigg).$

(3.9)

In this way, the period of the limited cycle can be approximated by

$T_{1}=2\pi\nu\Gamma\bigg(\frac{\lambda_{r}}{\epsilon^{2}}-\frac{1}{2}\bigg)/\bigg(\nu\lambda_{c}\Gamma\bigg(\frac{\lambda_{r}}{\epsilon^{2}}-\frac{1}{2}\bigg)-\kappa\epsilon^{2}\Gamma(\frac{\lambda_{r}}{\epsilon^{2}}+\frac{1}{2})\bigg).$

(3.10)

If $\lambda_{r} > \epsilon^{2}$, it is easy to check that the maximum of probability density function is located at

$r^{*}=\sqrt{\frac{\epsilon^{2}-\lambda_{r}}{\nu}},$

(3.11)

which means that $r^{*}$ is the mode of $r_{+}$. In this way, the period of the limited cycle can be approximated by

$T_{2}=\frac{2\pi\nu}{\lambda_{c}\nu+\kappa\epsilon^{2}-\kappa\lambda_{r}}.$

(3.12)

---

3.2. Stochastic Model with Internal Shock

In the last subsection, we introduce the financial shock, which is considered as an external noise, into system (2.15). In this subsection, we introduce another financial shock into system (2.15) and get the following system

$\left\{ \begin{split} &r'=(1+\epsilon\xi_{t})r(\lambda_{r}+\nu r^{2}),\\ &\Theta'=\lambda_{c}+\kappa r^{2}, \end{split} \right.$

(3.13)

where $\xi_{t}$ is a white noise. As the original equivalent solution $r=\sqrt{-\frac{\lambda_{r}}{\nu}}$ is still a solution of the stochastic model (3.13), we interpret the noise as an internal shock. In the following argument, we study the dynamics of system (3.13) in the framework of stochastic differential equations of ItÔ type and random dynamical system as well. We choose ItÔ interpretation and rewrite system (3.13) as

$\left\{ \begin{split} &dr=r(\lambda_{r}+\nu r^{2})dt+\epsilon r(\lambda_{r}+\nu r^{2})dB(t),\\ &d\Theta=(\lambda_{c}+\kappa r^{2})dt, \end{split} \right.$

(3.14)

where $B (t)$ is a Brownian motion. The random dynamical system $\Phi$ associating with (3.14) with initial value $r_{0}\geq0$ can be represented by

$\Phi(t,\omega)r_{0}=r_{0}+\int_{0}^{t}(\lambda_{r}\Phi(s,\omega)r_{0}+\nu\Phi^{3}(s,\omega)r_{0})ds+\epsilon\int_{0}^{t}(\lambda_{r}\Phi(s,\omega)r_{0}+\nu\Phi^{3}(s,\omega)r_{0})dB(s).$

(3.15)

Denote $r^{+}=\sqrt{-\frac{\lambda_{r}}{\nu}}$ and $r^{-}=-\sqrt{-\frac{\lambda_{r}}{\nu}}$. It is easy to see that system (3.15) admits three trivial invariant measures $\delta_{0}$, $\delta_{r^{+}}$ and $\delta_{r^{-}}$. We are just interested in the case of $r\geq0$. The following proposition tells the dynamics of system (3.15).

Proposition 3.2. Let $\Phi$ be the system in (3.15) with initial value $r_{0} > 0$. Then

Case Ⅰ. If $\epsilon^{2}\lambda_{r} < 2$, then $\Phi (t) r_{0}\rightarrow\sqrt{-\frac{\lambda_{r}}{\nu}}$ almost surely as $t\rightarrow\infty$, which implies that $\delta_{r^{+}}$ is a stable $\Phi$-invariant measure.

Case Ⅱ. If $\epsilon^{2}\lambda_{r} > 2$ and $r_{0} < \sqrt{-\frac{\lambda_{r}}{\nu}}$, then

$\mathbb{P}\bigg(\Phi(t)r_{0}\rightarrow\sqrt{-\frac{\lambda_{r}}{\nu}}~as~t\rightarrow\infty\bigg)=f(r_{0}^{2})/f\bigg(-\frac{\lambda_{r}}{\nu}\bigg)$

(3.16)

and

$\mathbb{P}(\Phi(t)r_{0}\rightarrow0~as~t\rightarrow\infty)=1-f(r_{0}^{2})/f\bigg(-\frac{\lambda_{r}}{\nu}\bigg),$

(3.17)

where

$f(x)=\int_{0}^{x}y^{-\big(\frac{1}{\epsilon^{2}\lambda_{r}}+\frac{1}{2}\big)}\bigg(-\frac{\lambda_{r}}{\nu}-y\bigg)^{\frac{1}{\epsilon^{2}\lambda_{r}}}dy.$

(3.18)

The proof of Proposition 3.2 can be found in Appendix C. The results of Proposition 3.2 tells that if the parameters of the system satisfy $\epsilon^{2}\lambda_{r} < 2$, the limited cycle $r=\sqrt{-\frac{\lambda_{r}}{\nu}}$ is stable. If $\epsilon^{2}\lambda_{r} > 2$, the limited cycle is stable in some probability less than one. The period of the limited cycle is the same as (2.16).

---

3.3. Stochastic Model with External and Internal Shocks

In the last two subsection, the dynamics of system (2.15) with external shock and internal shock are investigated respectively. In this subsection, we consider the system with both two kinds of shocks, namely that

$\left\{ \begin{split} &r'=(1+\epsilon_{2}\xi_{2t})r(\lambda_{r}+\nu r^{2})+\epsilon_{1}r\xi_{1t},\\ &\Theta'=\lambda_{c}+\kappa r^{2}, \end{split} \right.$

(3.19)

where $\xi_{1t}$ and $\xi_{2t}$ are white noises. Similarly, the stochastic differential equation of ItÔ type of (3.19) can be rewritten as

$\left\{ \begin{split} &dr=r(\lambda_{r}+\nu r^{2})dt+\epsilon_{1}rdB_{1}(t)+\epsilon_{2}r(\lambda_{r}+\nu r^{2})dB_{2}(t),\\ &d\Theta=(\lambda_{c}+\kappa r^{2})dt, \end{split} \right.$

(3.20)

where $B_{1}(t)$ and $B_{2}(t)$ are two Brownian motions satisfying $\langle B_{1}, B_{2}\rangle_{t}=\rho t$, $-1\leq\rho\leq1$. Dynamics of stochastic system with double noises can be referred to Huang (2016). The random dynamical system associating with (3.20) with initial value $r_{0} > 0$ can be represented by

$\begin{split} \Phi(t,\omega)r_{0}=&r_{0}+\int_{0}^{t}(\lambda_{r}\Phi(s,\omega)r_{0}+\nu\Phi^{3}(s,\omega)r_{0})ds+\epsilon_{1}\int_{0}^{t}\Phi(s,\omega)r_{0}dB_{1}(s)\\ &+\epsilon_{2}\int_{0}^{t}(\lambda_{r}\Phi(s,\omega)r_{0}+\nu\Phi^{3}(s,\omega)r_{0})dB_{2}(s). \end{split}$

(3.21)

The following proposition shows the dynamics of system (3.21).

Proposition 3.3. If $\gamma < \frac{3}{2}$, system $\Phi$ in (3.21) undergoes a stochastic pitchfork bifurcation at $\lambda_{r}=\frac{\alpha}{2}$ and undergoes a P-bifurcation at $\lambda_{r}=\alpha$. The probability density function of the generated non-trivial invariant measure $\delta_{r_{+}}$ supporting on $\mathbb{R}^{+}$ is given as

$\begin{split} p(r)=&\frac{2}{\sqrt{\alpha r^{2}+\beta r^{4}+\gamma r^{6}}}\exp\bigg(\int_{c}^{r}\frac{(2\lambda_{r}-\alpha)+(2\nu-2\beta)x^{2}-3\gamma x^{4}}{\alpha x+\beta x^{3}+\gamma x^{5}}dx\bigg)\\ =&Cr^{\frac{4\lambda_{r}-3\alpha}{\alpha}}(\alpha+\beta r^{2}+\gamma r^{4})^{-\frac{\alpha+\lambda}{\alpha}-\frac{1}{2}}\exp\bigg(\frac{4\alpha\nu-2\beta\lambda_{r}}{\alpha\sqrt{4\alpha\gamma-\beta^{2}}}\arctan\bigg(\frac{\beta+2\gamma x^{2}}{\sqrt{4\alpha\gamma-\beta^{2}}}\bigg)\bigg), \end{split}$

(3.22)

where

$\alpha=\epsilon_{1}^{2}+2\epsilon_{1}\epsilon_{2}\rho\lambda_{r}+\epsilon_{2}^{2}\lambda_{r}^{2},\beta=2\epsilon_{1}\epsilon_{2}\rho\nu+2\epsilon_{2}^{2}\lambda_{r}\nu,\gamma=\epsilon^{2}_{2}\nu^{2},$

(3.23)

$\begin{split} C=&\bigg(\int_{0}^{\infty}r^{\frac{4\lambda_{r}-3\alpha}{\alpha}}(\alpha+\beta r^{2}+\gamma r^{4})^{-\frac{\alpha+\lambda}{\alpha}-\frac{1}{2}}\exp\bigg(\frac{4\alpha\nu-2\beta\lambda_{r}}{\alpha\sqrt{4\alpha\gamma-\beta^{2}}}\arctan\bigg(\frac{\beta+2\gamma x^{2}}{\sqrt{4\alpha\gamma-\beta^{2}}}\bigg)\bigg)dr\bigg)^{-1}. \end{split}$

(3.24)

If $\gamma > \frac{3}{2}$, $\delta_{0}$ is the unique invariant measure. If $\lambda_{r} < \frac{\alpha}{2}$, then $\delta_{0}$ is stable. Otherwise, $\delta_{0}$ is unstable.

Detailed proof of Proposition 3.3 can be found in Appendix D. Returning to system (3.20), $r_{+}(\theta_{t}\omega)$ is an ergodic and stationary process, which can be regarded as a stochastic limited cycle of (3.20), corresponding to the deterministic limited cycle. The mean of $r_{+}$ is given as

$\begin{split} \mathbb{E}[r_{+}]=\int_{0}^{\infty}Cr^{\frac{4\lambda_{r}-2\alpha}{\alpha}}(\alpha+\beta r^{2}+\gamma r^{4})^{-\frac{\alpha+\lambda}{\alpha}-\frac{1}{2}}\exp\bigg(\frac{4\alpha\nu-2\beta\lambda_{r}}{\alpha\sqrt{4\alpha\gamma-\beta^{2}}}\arctan\bigg(\frac{\beta+2\gamma x^{2}}{\sqrt{4\alpha\gamma-\beta^{2}}}\bigg)\bigg)dr. \end{split}$

(3.25)

The mean of $r^{2}_{+}$ is given as

$\begin{split} \mathbb{E}[r_{+}^{2}]=\int_{0}^{\infty}Cr^{\frac{4\lambda_{r}-\alpha}{\alpha}}(\alpha+\beta r^{2}+\gamma r^{4})^{-\frac{\alpha+\lambda}{\alpha}-\frac{1}{2}}\exp\bigg(\frac{4\alpha\nu-2\beta\lambda_{r}}{\alpha\sqrt{4\alpha\gamma-\beta^{2}}}\arctan\bigg(\frac{\beta+2\gamma x^{2}}{\sqrt{4\alpha\gamma-\beta^{2}}}\bigg)\bigg)dr. \end{split}$

(3.26)

and so as $\mathbb{E}[\Theta'(t)]=\lambda_{c}+\kappa\mathbb{E}[r^{2}_{+}]$. The approximated period of limited cycle is given as

$T_{1}=\frac{2\pi}{\lambda_{c}+\kappa\int_{0}^{\infty}Cr^{\frac{4\lambda_{r}-\alpha}{\alpha}}(\alpha+\beta r^{2}+\gamma r^{4})^{-\frac{\alpha+\lambda}{\alpha}-\frac{1}{2}}\exp(\frac{4\alpha\nu-2\beta\lambda_{r}}{\alpha\sqrt{4\alpha\gamma-\beta^{2}}}\arctan(\frac{\beta+2\gamma x^{2}}{\sqrt{4\alpha\gamma-\beta^{2}}}))dr}.$

(3.27)

If $\lambda_{r} > \alpha$, the maximum of the probability density function is located at

$r_{*}=\sqrt{\frac{(\nu-2\beta)+\sqrt{(2\beta-\nu)^{2}-12\gamma(\alpha-\lambda_{r})}}{6\gamma}},$

(3.28)

which is the mode of $r_{+}$. The corresponding approximated period of limited cycle is given as

$T_{2}=\frac{12\pi\gamma}{6\lambda_{c}\gamma+\kappa(\nu-2\beta)+\kappa\sqrt{(2\beta-\nu)^{2}-12\gamma(\alpha-\lambda_{r})}}.$

(3.29)

---

4. Discussions

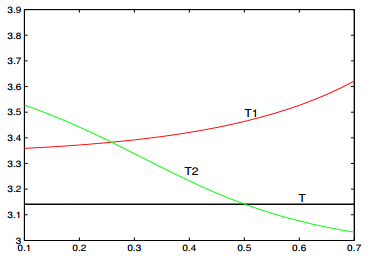
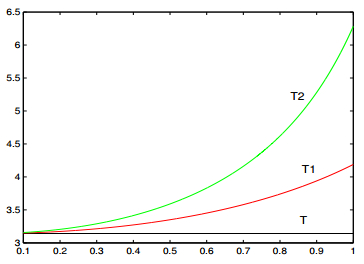
In Section 3, we have studied the dynamics of the business cycle model with external shock, internal shock, both external and internal shocks respectively in the framework of stochastic differential equations and random dynamical systems. The dynamics of the model can acquaint us with the effects of shocks on the business cycle. In the case of external shock, if the intensity of the shock $\epsilon$ satisfies $\epsilon^{2} < 2\lambda_{r}$, there exists an ergodic and stationary process $r_{+}(t)$ such that the original amplitude $r=\sqrt{-\frac{\lambda_{r}}{\nu}}$ of the business cycle transfers to $r_{+}(t)$, which volatilities randomly. The original velocity $\Theta'(t)=\frac{\lambda_{c}\nu-\kappa\lambda_{r}}{\nu}$ of the business cycle transfers to $\Theta'(t)=\lambda_{c}+\kappa r_{+}^{2}$, which is also stationary. By calculating the mean and mode of $\Theta'(t)$, we obtain two approximated estimations of period (3.10) and (3.12) in the case of external shock. Figure 1 shows the comparison among $T$, $T_{1}$ and $T_{2}$ as functions of $\epsilon$. We can see that $T_{1}$ and $T_{2}$ are both larger than $T$ for given an intensity of shock $\epsilon$, namely that the period of business cycle may be enlarged due to the external shock. As the intensity of shock increases, the period of business cycle increases as well. If the intensity of shock satisfies $\epsilon^{2} > 2\lambda_{r}$, the amplitude of the business cycle converges to $0$, which means that the economic system converges to a normalcy $(0, 0)$ (Actually, $(0, 0)$ is not the real normalcy. One could understand this from (2.3), (2.4) and the context).

In the case of internal shock, if the intensity of shock satisfies $\epsilon^{2} < \frac{2}{\lambda_{r}}$, the economic system admits the business cycle whose amplitude and velocity are the same as the original business cycle, so as the period.

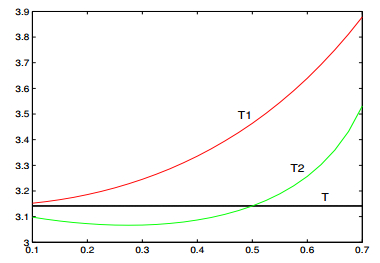
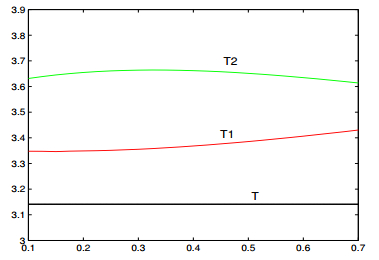
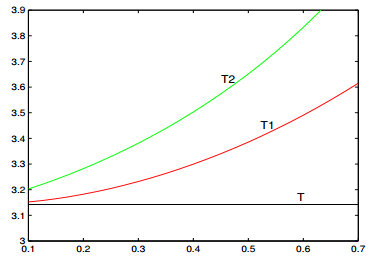
If the intensity of shock satisfies $\epsilon^{2} > \frac{2}{\lambda_{r}}$, the business cycle exists in some probability less than one. The system converges to a normalcy in residual probability. In summary, the system either behaves periodically or converges to a normalcy. It is uncertain. In the case of external and internal shocks acting on the system, the effects of shocks on the business cycle are more complicated. If the intensities of shocks $\epsilon_{1}$ and $\epsilon_{2}$ satisfy $2\lambda_{r} > \epsilon_{1}^{2}+2\epsilon_{1}\epsilon_{2}\rho\lambda_{r}+\epsilon_{2}^{2}\lambda_{r}^{2}$, $\epsilon_{2}^{2}\nu^{2} < \frac{3}{2}$, the economic system behaves randomly periodically as the case of external shock, namely that the original amplitude and velocity both transfer to stationary processes. We as well obtain two approximated periods given in (3.27) and (3.29). Figure 2 and Figure 3 show the comparison among $T$, $T_{1}$ and $T_{2}$ as functions of $\epsilon_{1}$ and $\epsilon_{2}$ respectively under the assumption that external shock and internal shock are positively correlation, namely that $\rho > 0$. Figure 4 and Figure 5 show the same topic but under the assumption that external shock and internal shock are negatively correlation, namely that $\rho < 0$. From the figures, we can see that $T_{1}$ is always larger than $T$ regardless of the correlation of shocks. From Figure 2 and Figure 4, we can see that $T_{2}$ may decrease as the intensity $\epsilon_{2}$ increases. In contrast, $T_{1}$ increases as $\epsilon_{2}$ increases. Figure 3 and Figure 5 tell that both $T_{1}$ and $T_{2}$ may increase as the intensity $\epsilon_{1}$ increases. On the other hand, from the increasing rate of $T_{1}$, $T_{2}$ and decreasing rate of $T_{2}$ as functions of $\epsilon_{1}$ and $\epsilon_{2}$ in the figures, we can see the sensitivity of the period of the business cycle on the intensities of shocks. If the intensities of shocks satisfy $2\lambda_{r} < \epsilon_{1}^{2}+2\epsilon_{1}\epsilon_{2}\rho\lambda_{r}+\epsilon_{2}^{2}\lambda_{r}^{2}$, $\epsilon_{2}^{2}\nu^{2} < \frac{3}{2}$, the economic system converges to the normalcy. However, if the intensities of shocks satisfy $2\lambda_{r} < \epsilon_{1}^{2}+2\epsilon_{1}\epsilon_{2}\rho\lambda_{r}+\epsilon_{2}^{2}\lambda_{r}^{2}$, $\epsilon_{2}^{2}\nu^{2} > \frac{3}{2}$, the normalcy looses its stability and the system becomes disorder, which may implies the upcoming of economic crisis.

---

A. The procedure of simplification of the system

To simplify the original system, denoting $\Lambda=\mathrm{arg}(\lambda)$, we can rewrite (2.11) as

$\left\{ \begin{split} \varphi'=&|\lambda|\cos2\pi\Lambda\varphi-|\lambda|\sin2\pi\Lambda\phi+\frac{\alpha}{2\lambda_{c}}I''(0)\varphi^{2}+\frac{\alpha}{6\lambda_{c}^{2}}I'''(0)\varphi^{3},\\ \phi'=&|\lambda|\sin2\pi\Lambda\varphi+|\lambda|\cos2\pi\Lambda\phi-\frac{\alpha q}{2\lambda_{c}^{2}}I''(0)\varphi^{2}+\frac{\alpha q}{6\lambda_{c}^{3}}I'''(0)\varphi^{3}. \end{split} \right.$

(A.1)

Then making the transformation of coordinates

$\varphi=\frac{1}{2}z+\frac{1}{2}\overline{z},~\phi=-\frac{1}{2}z\mathbf{i}+\frac{1}{2}\overline{z}\mathbf{i},$

(A.2)

that is

$z=\varphi+\phi\mathbf{i},~\overline{z}=\varphi-\phi\mathbf{i},$

(A.3)

system (A.1) is translated into the following forms:

$\left\{ \begin{array}{l} z' = \lambda z + {a_{20}}{z^2} + 2{a_{11}}z\bar z + {a_{02}}{{\bar z}^2} + {b_{30}}{z^3} + 3{b_{21}}{z^2}\bar z + 3{b_{12}}z{{\bar z}^2} + {b_{03}}{{\bar z}^3},\\ \bar z' = - \lambda \bar z + \overline {{a_{20}}} {z^2} + 2\overline {{a_{11}}} z\bar z + \overline {{a_{02}}} {{\bar z}^2} + \overline {{b_{30}}} {z^3} + 3\overline {{b_{21}}} {z^2}\bar z + 3\overline {{b_{12}}} z{{\bar z}^2} + \overline {{b_{03}}} {{\bar z}^3}, \end{array} \right.$

(A.4)

where

$a:=a_{20}=a_{11}=a_{02}=\frac{\alpha}{8\lambda_{c}}I''(0)-\frac{\alpha(q+\lambda_{r})}{8\lambda_{c}^{2}}I''(0)\mathbf{i},$

(A.5)

$b:=b_{30}=b_{21}=b_{12}=b_{03}=\frac{\alpha}{48\lambda_{c}^{2}}I'''(0)-\frac{\alpha(q+\lambda_{r})}{48\lambda_{c}^{3}}I'''(0)\mathbf{i},$

(A.6)

Denote $h_{2}(z, \overline{z})=h_{220}z^{2}+h_{211}z\overline{z}+h_{202}\overline{z}^{2}$. Replacing $z$ by $z+h_{2}(z, \overline{z})$ gives

$\begin{split} z'\bigg(1+\frac{\partial h_{2}}{\partial z}\bigg)=\lambda z+\lambda\frac{\partial h_{2}}{\partial\overline{z}}\overline{z}+\lambda h_{2}+a_{20}z^{2}+2a_{11}z\overline{z}+a_{02}\overline{z}^{2}+O(z^{3},\overline{z}^{3}). \end{split}$

(A.7)

Therefore, $h_{2}$ satisfies

$-\lambda\frac{\partial h_{2}}{\partial z}z+\lambda\frac{\partial h_{2}}{\partial\overline{z}}\overline{z}+\lambda h_{2}+a_{20}z^{2}+2a_{11}z\overline{z}+a_{02}\overline{z}^{2}=0.$

(A.8)

It is easy to solve that

$h_{220}=\frac{a_{20}}{\lambda},~h_{211}=-\frac{2a_{11}}{\lambda},~h_{202}=-\frac{a_{02}}{3\lambda}.$

(A.9)

Omitting the high order terms, system (A.4) is translated to

$z'=\lambda z+f_{30}z^{3}+f_{21}z^{2}\overline{z}+f_{12}z\overline{z}^{2}+f_{03}\overline{z}^{3},$

(A.10)

where

$\left\{ \begin{split} &f_{30}=b_{30}-2\lambda h_{220}^{2}-2h_{220}a_{20},\\ &f_{21}=3b_{21}-5\lambda h_{220}h_{211}-h_{211}a_{20}-4h_{220}a_{11},\\ &f_{12}=3b_{12}-6\lambda h_{220}h_{202}-2\lambda h_{211}^{2}-2h_{211}a_{11}-2h_{220}a_{02},\\ &f_{03}=b_{03}-3\lambda h_{211}h_{202}-h_{211}a_{02}. \end{split} \right.$

(A.11)

Repeating the procedure above, denote $h_{3}(z, \overline{z})=h_{330}z^{3}+h_{321}z^{2}\overline{z}+h_{312}z\overline{z}^{2}+h_{303}\overline{z}^{3}$. Replacing $z$ by $z+h_{3}(z, \overline{z})$, then $h_{3}$ must satisfy

$-\lambda\frac{\partial h_{3}}{\partial z}z+\lambda\frac{\partial h_{3}}{\partial\overline{z}}\overline{z}+\lambda h_{3}+f_{30}z^{3}+f_{21}z^{2}\overline{z}+f_{12}z\overline{z}^{2}+f_{03}\overline{z}^{3}=0.$

(A.12)

It is easy to solve that

$h_{330}=\frac{f_{30}}{2\lambda},~h_{321}=0,~h_{312}=-\frac{f_{12}}{2\lambda},~h_{303}=-\frac{f_{03}}{4\lambda}.$

(A.13)

Omitting the high order terms, system (A.10) is translated to

$z'=\lambda z+f_{21}z^{2}\overline{z}.$

(A.14)

Recalling that $z=\varphi+\phi\mathbf{i}$, then we have

$\left\{ \begin{split} &\varphi'=\lambda_{r}\varphi-\lambda_{c}\phi+(\nu\varphi-\kappa\phi)(\varphi^{2}+\phi^{2}),\\ &\phi'=\lambda_{c}\varphi+\lambda_{r}\phi+(\kappa\varphi+\nu\phi)(\varphi^{2}+\phi^{2}),\\ \end{split} \right.$

(A.15)

where $\nu=Re f_{21}$, $\kappa=Im f_{21}$. From the arguments above, we can get

$\nu=\frac{\alpha I'''(0)}{16\lambda_{c}^{2}}-\frac{\alpha^{2}I''^{2}(0)}{8|\lambda|^{2}\lambda_{c}^{2}}\bigg(2q+\lambda_{r}+\frac{(q+\lambda_{r})^{2}\lambda_{r}}{\lambda_{c}^{2}}\bigg)$

(A.16)

and

$\kappa=-\frac{\alpha(q+\lambda_{r})I'''(0)}{16\lambda^{3}_{c}}+\frac{\alpha^{2}I''^{2}(0)}{4|\lambda|^{2}\lambda_{c}}\bigg(-\frac{(q+\lambda_{r})\lambda_{r}}{\lambda_{c}^{2}}+\frac{(q+\lambda_{r})^{2}}{2\lambda_{c}^{2}}-\frac{1}{2}\bigg).$

(A.17)

---

B. Proof of Proposition 3.1

The backward cocycle over $\widetilde{\theta}:=\theta^{-1}$ corresponding to (3.2) is given by $\widetilde{\Phi}(t, \omega) r_{0}:=\Phi (-t, \omega) r_{0}$. It is generated by the stochastic differential equation

$d\widetilde{r}=-\lambda_{r}\widetilde{r}dt-\nu\widetilde{r}^{3}dt+\epsilon\widetilde{r}dB(-t).$

(B.1)

First we restrict system $\Phi$ on $\mathbb{R}^{+}$. The Fokker-Plank equations of (3.2) and (B.1) are given respectively as

$\frac{\partial}{\partial t}p(t,r)=\frac{\partial^{2}}{\partial r^{2}}\bigg(\frac{\epsilon^{2}}{2}r^{2}p(t,r)\bigg)-\frac{\partial}{\partial r}((\lambda_{r}r+\nu r^{3})p(t,r))$

(B.2)

and

$\frac{\partial}{\partial t}\widetilde{p}(t,r)=\frac{\partial^{2}}{\partial r^{2}}\bigg(\frac{\epsilon^{2}}{2}r^{2}\widetilde{p}(t,r)\bigg)+\frac{\partial}{\partial r}((\lambda_{r}r+\nu r^{3})\widetilde{p}(t,r)),$

(B.3)

whose time-homogeneous solutions can be solved by

$p(r)=Cr^{(2\lambda_{r}-2\epsilon^{2})/\epsilon^{2}}\exp\bigg(\frac{\nu}{\epsilon^{2}}r^{2}\bigg),~\widetilde{p}(r)=Cr^{-\frac{2\lambda_{r}}{\epsilon^{2}}}\exp\bigg(-\frac{\nu}{\epsilon^{2}}r^{2}\bigg).$

(B.4)

Then $m (dr)=p (r) dr$ is the speed measure of $\Phi$, which is an invariant measure of Markov semigroup $P_{t}$ associating with (3.2). $\widetilde{m}(dr)=\widetilde{p}(r) dr$ is the speed measure of $\widetilde{\Phi}$, which is an invariant measure of Markov semigroup $\widetilde{P}_{t}$ associating with (B.1). Recall from Chapter 2 in Crauel and Gundlach (1999) that there is a bijection between the invariant probability measures of the semigroup and the $\Phi$-invariant measures. If $\lambda_{r} < \frac{\epsilon^{2}}{2}$, $m (\mathbb{R}^{+})$ and $\widetilde{m}(\mathbb{R}^{+})=\infty$, which both can not be normalized. We conclude that there is no other $\Phi$-invariant measures except $\delta_{0}$. To see the stability of invariant measure, we can calculate the Lyapunov exponent. The linearization of $\Phi$, $D\Phi (t, r)$ satisfies

$dD\Phi(t,r)=(\lambda_{r}+2\nu r^{2})D\Phi(t,r)dt+\epsilon D\Phi(t,r)dB(t)$

(B.5)

with solution

$D\Phi(t,r)v=v\exp\bigg(\int_{0}^{t}\bigg(\lambda_{r}-\frac{\epsilon^{2}}{2}+2\nu r^{2}(s)\bigg)ds+\epsilon B(t)\bigg).$

(B.6)

The Lyapunov exponent of $\delta_{0}$ satisfies

$\begin{split} \lambda_{\Phi}(\delta_{0})=&\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\log D\Phi(t,0)\\ =&\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\log\exp\bigg(\int_{0}^{t}\bigg(\lambda_{r}-\frac{\epsilon^{2}}{2}+2\nu\cdot 0\bigg)ds+\epsilon B(t)\bigg)\\ =&\lambda_{r}-\frac{\epsilon^{2}}{2}<0, \end{split}$

(B.7)

which implies that $\delta_{0}$ is stable. If $\lambda_{r} > \frac{\epsilon^{2}}{2}$, then $m (\mathbb{R}^{+}) < \infty$ and $\widetilde{m}(\mathbb{R}^{+})=\infty$. Moreover, for any $c > 0$, $\widetilde{m}(\mathbb{R}^{+}/[0, c])=\infty$, which implies that $\Phi$ is forward complete (see Lemma 2.6 in Chapter 2 in Crauel and Gundlach (1999)). Hence, there exists a random variable, denoted by $r_{+}$, such that $\delta_{r_{+}(\omega)}=\underset{t\rightarrow\infty}{\lim}\Phi (t, \widetilde{\theta}_{t}\omega) m/m (\mathbb{R}^{+})$ is an ergodic $\Phi$-invariant measure. Moreover,

$r(\omega)=1/\bigg(-2\nu\int_{-\infty}^{0}\exp(2\lambda_{r}s-\epsilon^{2}s+2\epsilon B(s))ds\bigg)^{\frac{1}{2}}$

(B.8)

and

$r(\theta_{t}\omega)=\exp\bigg(\lambda_{r} t-\frac{\epsilon^{2}}{2}t+\epsilon B(t)\bigg)/\bigg(-2\nu\int_{-\infty}^{t}\exp(2\lambda_{r}s-\epsilon^{2}s+2\epsilon B(s))ds\bigg)^{\frac{1}{2}}.$

(B.9)

The system occurs a D-bifurcation at $\lambda_{r}=\frac{\epsilon^{2}}{2}$. To see the stability of $\delta_{r_{+}}$, we first give an estimation. Denote $R (r)=r^{2}(t)$, where $r$ is the solution of (3.2) with initial value $r_{0} > 0$. Then $R$ satisfies

$R(t)=\exp(2\lambda_{r} t-\epsilon^{2}t+2\epsilon B(t))/\bigg(\frac{1}{r_{0}^{2}}-2\nu\int_{0}^{t}\exp(2\lambda_{r}s-\epsilon^{2}s+2\epsilon B(s))ds\bigg).$

(B.10)

Denote

$Z(t)=\frac{1}{r_{0}^{2}}-2\nu\int_{0}^{t}\exp(2\lambda_{r}s-\epsilon^{2}s+2\epsilon B(s))ds.$

(B.11)

It is easy to see that

$\int_{0}^{t}R(s)ds=-\frac{1}{2\nu}\log Z(t)+\frac{1}{2\nu}\log Z(0).$

(B.12)

By Doob's inequality

$\mathbb{P}\bigg(\underset{0\leq s\leq t}{\sup}|B(s)|\geq ht\bigg)\leq\exp\bigg(-\frac{h^{2}}{2}t\bigg),~\forall h>0,$

(B.13)

we have

$\begin{split} &\mathbb{P}\bigg(\frac{1}{r^{2}_{0}}-\frac{2\nu}{2\lambda_{r}-\epsilon^{2}}\exp((2\lambda_{r}-\epsilon^{2}-2\epsilon h)t)+\frac{2\nu}{2\lambda_{r}-\epsilon^{2}}\exp(-2\epsilon ht)\leq Z(t)\\ &\leq\frac{1}{r^{2}_{0}}-\frac{2\nu}{2\lambda_{r}-\epsilon^{2}}\exp((2\lambda_{r}-\epsilon^{2}+2\epsilon h)t)+\frac{2\nu}{2\lambda_{r}-\epsilon^{2}}\exp(2\epsilon ht)\bigg)\geq1-\exp\bigg(-\frac{h^{2}}{2}t\bigg). \end{split}$

(B.14)

It is easy to see that there exists $T > 0$, such that for $t\geq T$,

$\begin{split} &\mathbb{P}\bigg(-\frac{2\nu}{2\lambda_{r}-\epsilon^{2}}\exp((2\lambda_{r}-\epsilon^{2}-2\epsilon h)t)\leq Z(t)\leq-\frac{2\nu}{2\lambda_{r}-\epsilon^{2}}\exp((2\lambda_{r}-\epsilon^{2}+2\epsilon h)t)\bigg)\\ &\geq1-\exp\bigg(-\frac{h^{2}}{2}t\bigg), \end{split}$

(B.15)

that is

$\begin{split} &\mathbb{P}\bigg(-\frac{1}{2\nu}\log\bigg(-\frac{2\nu}{2\lambda_{r}-\epsilon^{2}}\bigg)-\frac{1}{2\nu}(2\lambda_{r}-\epsilon^{2}-2\epsilon h)t\leq-\frac{1}{2\nu}\log Z(t)\\ &\leq-\frac{1}{2\nu}\log\bigg(-\frac{2\nu}{\lambda_{r}-\epsilon^{2}}\bigg)-\frac{1}{2\nu}(2\lambda_{r}-\epsilon^{2}+2\epsilon h)t\bigg)\geq1-\exp\bigg(-\frac{h^{2}}{2}t\bigg), \end{split}$

(B.16)

which implies

$-\frac{1}{2\nu}(2\lambda_{r}-\epsilon^{2}-2\epsilon h)\leq-\frac{1}{2\nu}\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\log Z(t)\leq-\frac{1}{2\nu}(2\lambda_{r}-\epsilon^{2}+2\epsilon h).$

(B.17)

Since $h$ is arbitrary, we have

$\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\int_{0}^{t}R(s)ds=-\frac{1}{2\nu}\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\log Z(t)=\frac{1}{2\nu}(\epsilon^{2}-2\lambda_{r})$

(B.18)

almost surely. Applying this result, the Lyapunov exponent of $\lambda_{\Phi}(\delta_{r_{+}})$ satisfies

$\begin{split} \lambda_{\Phi}(\delta_{r_{+}})=&\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\log D\Phi(t,r_{+})\\ =&\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\int_{0}^{t}\bigg(\lambda_{r}-\frac{\epsilon^{2}}{2}+2\nu r_{+}^{2}(\theta_{s}\omega)\bigg)ds\\ =&\lambda_{r}-\frac{\epsilon^{2}}{2}+2\nu\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\int_{0}^{t}r_{+}^{2}(\theta_{s}\omega)ds\\ =&\lambda_{r}-\frac{\epsilon^{2}}{2}-2\lambda_{r}+\epsilon^{2}\\ =&-\lambda_{r}+\frac{\epsilon^{2}}{2}<0, \end{split}$

(B.19)

which implies that $\delta_{r_{+}}$ is stable. At the same time, $\delta_{0}$ becomes unstable. If $\frac{\epsilon^{2}}{2} < \lambda_{r} < \epsilon^{2}$, the maximum of $p$ is located at $r=0$. If $\lambda_{r} > \epsilon^{2}$, the maximum of $p$ is located at $r^{*}$, where

$r^{*}=\sqrt{\frac{\epsilon^{2}-\lambda_{r}}{\nu}}.$

(B.20)

Therefore the system occurs a P-bifurcation at $\lambda_{r}=\epsilon^{2}$. Restricting $\Phi$ on $\mathbb{R}^{-}$ and following the arguments above, similarly, we can obtain another ergodic $\Phi$-invariant measure, denoted by $\delta_{r_{-}}$, which is also stable. Hence, we conclude that the system occurs a pitchfork bifurcation at $\lambda_{r}=\frac{\epsilon^{2}}{2}$.

---

C. Proof of Proposition 3.2

Denote $R (t)=r^{2}(t)$. Then by ItÔ's formula, we have

$dR=R(2+\lambda_{r}\epsilon^{2}+\epsilon^{2}\nu R)(\lambda_{r}+\nu R)dt+2\epsilon R(\lambda_{r}+\nu R)dB(t).$

(C.1)

Denote $Y (t)=\log\frac{R (t)}{\lambda_{r}+\nu R (t)}=\log R (t)-\log (\lambda_{r}+\nu R (r))$. Again by ItÔ's formula, we have

$dY=(2\lambda_{r}-\epsilon^{2}\lambda_{r}^{2}-3\lambda_{r}\epsilon^{2}\nu R)dt+2\epsilon\lambda_{r}dB(t),$

(C.2)

or

$\log\frac{R(t)}{\lambda_{r}+\nu R(t)}=\log\frac{R_{0}}{\lambda_{r}+\nu R_{0}}+(2\lambda_{r}-\epsilon^{2}\lambda_{r}^{2})t-3\lambda_{r}\epsilon^{2}\nu\int_{0}^{t}R(s)ds+2\epsilon\lambda_{r}B(t),$

(C.3)

where we have assumed that $B (0)=0$. By Doob's inequality (C.4), we have

$\mathbb{P}\bigg(\log\frac{R(t)}{\lambda_{r}+\nu R(t)}\geq\log\frac{R_{0}}{\lambda_{r}+\nu R_{0}}+(2\lambda_{r}-\epsilon^{2}\lambda_{r}^{2})t-2\epsilon\lambda_{r}ht\bigg)\geq1-\exp\bigg(-\frac{h^{2}}{2}t\bigg),$

(C.4)

where $R_{0} > 0$ is the initial condition. Since $\epsilon^{2}\lambda_{r} < 2$, namely $2\lambda_{r}-\epsilon^{2}\lambda_{r}^{2} > 0$ and $h > 0$ is arbitrary, we have

$\underset{t\rightarrow\infty}{\underline{\lim}}\log\frac{R(t)}{\lambda_{r}+\nu R(t)}\geq\log\frac{R_{0}}{\lambda_{r}+\nu R_{0}}+\underset{t\rightarrow\infty}{\underline{\lim}}(2\lambda_{r}-\epsilon^{2}\lambda_{r}^{2}-2\epsilon\lambda_{r}h)t=\infty$

(C.5)

almost surely, which is possible only if $\underset{t\rightarrow\infty}{\lim}R (t)=-\frac{\lambda_{r}}{\nu}$ almost surely.

For a function $f\in C^{2}(\mathbb{R}^{+})$, by ItÔ's formula, we have

$\begin{split} df(R)=&f'(R)dR+\frac{1}{2}f''(R)d\langle R\rangle\\ =&f'(R)R(2+\lambda_{r}\epsilon^{2}+\epsilon^{2}\nu R)(\lambda_{r}+\nu R)dt+2\epsilon f'(R)R(\lambda_{r}+\nu R)dB(t)\\ &+2\epsilon^{2}f''(R)R^{2}(\lambda_{r}+\nu R)^{2}dt. \end{split}$

(C.6)

Letting $f$ satisfy

$f'(R)R(2+\lambda_{r}\epsilon^{2}+\epsilon^{2}\nu R)(\lambda_{r}+\nu R)+2\epsilon^{2}f''(R)R^{2}(\lambda_{r}+\nu R)^{2}=0,$

(C.7)

we can solve that

$f(R)=\int_{0}^{R}x^{-\big(\frac{1}{\epsilon^{2}\lambda_{r}}+\frac{1}{2}\big)}\bigg(-\frac{\lambda_{r}}{\nu}-x\bigg)^{\frac{1}{\epsilon^{2}\lambda_{r}}}dx.$

(C.8)

For $0 < R_{0} < -\frac{\lambda_{r}}{\nu}$,

$\underset{t\rightarrow\infty}{\lim}\mathbb{E}[f(R(t))]=f\bigg(-\frac{\lambda_{r}}{\nu}\bigg)\mathbb{P}\bigg(R(t)\rightarrow-\frac{\lambda_{r}}{\nu}~as~t\rightarrow\infty\bigg).$

(C.9)

On the other hand, since $f (R (t))$ is a martingale, we have

$f(R_{0})=f\bigg(-\frac{\lambda_{r}}{\nu}\bigg)\mathbb{P}\bigg(R(t)\rightarrow-\frac{\lambda_{r}}{\nu}~as~t\rightarrow\infty\bigg),$

(C.10)

namely that

$\mathbb{P}\bigg(R(t)\rightarrow-\frac{\lambda_{r}}{\nu}~as~t\rightarrow\infty\bigg)=f(R_{0})/f\bigg(-\frac{\lambda_{r}}{\nu}\bigg),$

(C.11)

which implies that

$\mathbb{P}(R(t)\rightarrow0~as~t\rightarrow\infty)=1-f(R_{0})/f\bigg(-\frac{\lambda_{r}}{\nu}\bigg).$

(C.12)

---

D. Proof of Proposition 3.3

Making the transformation

$\left\{ \begin{split} &B_{1}(t)=\widetilde{B}_{1}(t),\\ &B_{2}(t)=\rho\widetilde{B}_{1}(t)+\sqrt{1-\rho^{2}}\widetilde{B}_{2}(t), \end{split} \right.$

(D.1)

it is easy to check that $\langle\widetilde{B}_{1}, \widetilde{B}_{2}\rangle=0$, namely that $\widetilde{B}_{1}$ and $\widetilde{B}_{2}$ are mutually independent Brownian motions. First equation in system (3.20) can be rewritten as

$dr=r(\lambda_{r}+\nu r^{2})dt+(\epsilon_{1}r+\rho\epsilon_{2}r(\lambda_{r}+\nu r^{2}))d\widetilde{B}_{1}(t)+\sqrt{1-\rho^{2}}\epsilon_{2}r(\lambda_{r}+\nu r^{2})d\widetilde{B}_{2}(t),$

(D.2)

which is equivalent in law to the following equation

$dx=\bigg(\bigg(\lambda_{r}-\frac{\alpha}{2}\bigg)x+(\nu-\beta)x^{3}-\frac{3}{2}\gamma x^{5}\bigg)dt+\sqrt{\alpha x^{2}+\beta x^{4}+\gamma x^{6}}\circ d\widetilde{B}(t),$

(D.3)

where

$\alpha=\epsilon_{1}^{2}+2\epsilon_{1}\epsilon_{2}\rho\lambda_{r}+\epsilon_{2}^{2}\lambda_{r}^{2},\beta=2\epsilon_{1}\epsilon_{2}\rho\nu+2\epsilon_{2}^{2}\lambda_{r}\nu,\gamma=\epsilon^{2}_{2}\nu^{2},$

(D.4)

associating with random dynamical system $\widetilde{\Phi}$ represented by

$\begin{split} \Psi(t,\omega)x_{0}=&x_{0}+\int_{0}^{t}\bigg(\bigg(\lambda_{r}-\frac{\alpha}{2}\bigg)\Psi(s,\omega)x_{0}+(\nu-\beta)\Psi^{3}(s,\omega)x_{0}-\frac{3}{2}\gamma \Psi^{5}(s,\omega)x_{0}\bigg)ds\\ &+\int_{0}^{t}\sqrt{\alpha\Psi^{2}(s,\omega)x_{0}+\beta\Psi^{4}(s,\omega)x_{0}+\gamma\Psi^{6}(s,\omega)x_{0}}\circ d\widetilde{B}(s) \end{split}$

(D.5)

with initial value $x_{0} > 0$. The backward cocycle over $\widetilde{\theta}$ corresponding to (D.5) is given by $\widetilde{\Psi}(t, \omega) x_{0}:=\Psi (-t, \omega) x_{0}$, which is generated by the stochastic differential equation

$d\widetilde{x}=\bigg(-\bigg(\lambda_{r}-\frac{\alpha}{2}\bigg)\widetilde{x}-(\nu-\beta)\widetilde{x}^{3}+\frac{3}{2}\gamma \widetilde{x}^{5}\bigg)dt+\sqrt{\alpha \widetilde{x}^{2}+\beta \widetilde{x}^{4}+\gamma \widetilde{x}^{6}}\circ d\widetilde{B}(-t).$

(D.6)

The Fokker-Plank equations of (D.3) and (D.6) can be written as

$\frac{\partial}{\partial t}p(t,x)=\frac{\partial^{2}}{\partial x^{2}}\bigg(\frac{1}{2}(\alpha x^{2}+\beta x^{4}+\gamma x^{6})p(t,x)\bigg)-\frac{\partial}{\partial x}((\lambda_{r}x+\nu x^{3})p(t,x))$

(D.7)

and

$\frac{\partial}{\partial t}\widetilde{p}(t,x)=\frac{\partial^{2}}{\partial x^{2}}\bigg(\frac{1}{2}(\alpha x^{2}+\beta x^{4}+\gamma x^{6})\widetilde{p}(t,x)\bigg)+\frac{\partial}{\partial x}((\lambda_{r}x+\nu x^{3})\widetilde{p}(t,x)),$

(D.8)

whose time-homogeneous solutions can be solved by

$p(x)=\frac{2}{\sqrt{\alpha x^{2}+\beta x^{4}+\gamma x^{6}}}\exp\bigg(2\int_{c}^{x}\frac{(\lambda_{r}-\frac{\alpha}{2})y+(\nu-\beta)y^{3}-\frac{3}{2}\gamma y^{5}}{\alpha y^{2}+\beta y^{4}+\gamma y^{6}}dy\bigg)$

(D.9)

and

$\widetilde{p}(x)=\frac{2}{\sqrt{\alpha x^{2}+\beta x^{4}+\gamma x^{6}}}\exp\bigg(2\int_{c}^{x}\frac{-(\lambda_{r}-\frac{\alpha}{2})y-(\nu-\beta)y^{3}+\frac{3}{2}\gamma y^{5}}{\alpha y^{2}+\beta y^{4}+\gamma y^{6}}dy\bigg).$

(D.10)

$m (dx)=p (x) dx$ is an invariant measure of the Markov semigroup associating with (D.3) and $\widetilde{m}(dx)=\widetilde{p}(x) dx$ is an invariant measure of Markov semigroup associating with (D.6). If $x > 0$ is small enough, it is easy to see that

$\begin{split} \exp\bigg(2\int_{c}^{x}\frac{(\lambda_{r}-\frac{\alpha}{2})y+(\nu-\beta)y^{3}-\frac{3}{2}y^{5}}{\alpha y^{2}+\beta y^{4}+\gamma y^{6}}dy\bigg)\approx\exp\bigg(\frac{2\lambda_{r}-\alpha}{\alpha}\int_{c}^{x}\frac{1}{y}dy\bigg)=Cx^{\frac{2\lambda_{r}-\alpha}{\alpha}} \end{split}$

(D.11)

and

$\begin{split} \exp\bigg(2\int_{c}^{x}\frac{-(\lambda_{r}-\frac{\alpha}{2})y-(\nu-\beta)y^{3}+\frac{3}{2}y^{5}}{\alpha y^{2}+\beta y^{4}+\gamma y^{6}}dy\bigg)\approx\exp\bigg(\frac{\alpha-2\lambda_{r}}{\alpha}\int_{c}^{x}\frac{1}{y}dy\bigg)=Cx^{\frac{\alpha-2\lambda_{r}}{\alpha}}, \end{split}$

(D.12)

which implies that for $x > 0$ is small enough, $p (x)\approx Cx^{\frac{2\lambda_{r}-2\alpha}{\alpha}}$ and $\widetilde{p}(x)\approx Cx^{-\frac{2\lambda_{r}}{\alpha}}$. If $x > 0$ is large enough, it is easy to see that

$\begin{split} \exp\bigg(2\int_{c}^{x}\frac{(\lambda_{r}-\frac{\alpha}{2})y+(\nu-\beta)y^{3}-\frac{3}{2}y^{5}}{\alpha y^{2}+\beta y^{4}+\gamma y^{6}}dy\bigg)\approx\exp\bigg(-\frac{3}{\gamma}\int_{c}^{x}\frac{1}{y}dy\bigg)=Cx^{-\frac{3}{\gamma}} \end{split}$

(D.13)

and

$\begin{split} \exp\bigg(2\int_{c}^{x}\frac{-(\lambda_{r}-\frac{\alpha}{2})y-(\nu-\beta)y^{3}+\frac{3}{2}y^{5}}{\alpha y^{2}+\beta y^{4}+\gamma y^{6}}dy\bigg)\approx\exp\bigg(\frac{3}{\gamma}\int_{c}^{x}\frac{1}{y}dy\bigg)=Cx^{\frac{3}{\gamma}}, \end{split}$

(D.14)

which implies that for $x > 0$ large enough, $p (x)\approx Cx^{-3-\frac{3}{\gamma}}$ and $\widetilde{p}(x)\approx Cx^{-3+\frac{3}{\gamma}}$. If $\lambda_{r} > \frac{\alpha}{2}$, $m (\mathbb{R}^{+}) < \infty$ and $\widetilde{m}(\mathbb{R}^{+})=\infty$. If $\gamma < \frac{3}{2}$, then for any $c > 0$, $\widetilde{m}(\mathbb{R}^{+}/[0, c])=\infty$. From Lemma 2.6 in Chapter 2 in Crauel and Gundlach (1999), $\Psi$ is forward complete. Hence, there exists a random variable $x_{+}$ such that $\delta_{x_{+}}=\underset{t\rightarrow\infty}{\lim}\Psi (t, \widetilde{\theta}_{t}\omega) m/m (\mathbb{R}^{+})$ is an ergodic invariant measure. If $\lambda_{r} < \frac{\alpha}{2}$, $\gamma > \frac{3}{2}$, then $\widetilde{m}(\mathbb{R}^{+}) < \infty$ and $m (\mathbb{R}^{+})=\infty$. But for any $c > 0$, $m (\mathbb{R}^{+}/[0, c]) < \infty$, which implies that $\Psi$ is not backward complete. Hence, there is no other invariant measures except $\delta_{0}$. We conclude that system occurs a D-bifurcation at $\lambda_{r}=\frac{\alpha}{2}$, $\gamma=\frac{3}{2}$. Now let $\gamma < \frac{3}{2}$. If $\frac{\alpha}{2} < \lambda_{r} < \alpha$, the maximum of $p$ is located at $0$. If $\lambda_{r} > \alpha$, the maximum of $p$ is located at $x_{*}$, where $x_{*}$ satisfies

$3\gamma x^{4}_{*}+(2\beta-\nu)x^{2}_{*}+\alpha-\lambda_{r}=0,$

(D.15)

which can be solved as

$x_{*}=\sqrt{\frac{(\nu-2\beta)+\sqrt{(2\beta-\nu)^{2}-12\gamma(\alpha-\lambda_{r})}}{6\gamma}}.$

(D.16)

We conclude that system occurs a P-bifurcation at $\lambda_{r}=\alpha$. The aforesaid results for $\Psi$ hold for $\Phi$ as well, namely that $\Phi$ occurs D-bifurcation at $\lambda_{r}=\frac{\alpha}{2}$, $\gamma=\frac{3}{2}$. We denote the generated non-trivial invariant measure as $\delta_{r_{+}}$. $\Phi$ occurs P-bifurcation at $\lambda_{r}=\alpha$, the maximum of the probability density function is located at $r_{*}=x_{*}$. To see the stabilities of the invariant measures, we calculate the Lyapunov exponents. The linearization of $\Phi$, $D\Phi (t, r)$ satisfies

$\begin{split} dD\Phi(t,r)=&(\lambda_{r}+3\nu r^{2})D\Phi(t,r)dt+(\epsilon_{1}+\rho\epsilon_{2}\lambda_{r}+3\rho\epsilon_{2}\nu r^{2})D\Phi(t,r)d\widetilde{B}_{1}(t)\\ &+\sqrt{1-\rho^{2}}\epsilon_{2}(\lambda_{r}+3\nu r^{2})D\Phi(t,r)d\widetilde{B}_{2}(t). \end{split}$

(D.17)

By ItÔ's formula, it is easy to check that

$\begin{split} \frac{1}{t}\log D\Phi(t,r)v=&\frac{1}{t}\log v+\lambda_{r}+3\nu\frac{1}{t}\int_{0}^{t}r^{2}(s)ds-\frac{1}{2t}\int_{0}^{t}(\epsilon_{1}+\rho\epsilon_{2}\lambda_{r}+3\rho\epsilon_{2}\nu r^{2}(s))^{2}ds\\ &-\frac{1}{2}(1-\rho^{2})\epsilon_{2}^{2}\frac{1}{t}\int_{0}^{t}(\lambda_{r}+3\nu r^{2}(s))^{2}ds\\ &+\frac{1}{t}\int_{0}^{t}(\epsilon_{1}+\rho\epsilon_{2}\lambda_{r}+3\rho\epsilon_{2}\nu r^{2}(s))d\widetilde{B}_{1}(s)\\ &+\sqrt{1-\rho^{2}}\epsilon_{2}\frac{1}{t}\int_{0}^{t}(\lambda_{r}+3\nu r^{2}(s))d\widetilde{B}_{2}(s)\\ =&\frac{1}{t}\log V+\lambda_{r}-\frac{\alpha}{2}+3\bigg(\nu-\frac{\beta}{2}\bigg)\frac{1}{t}\int_{0}^{t}r^{2}(s)ds-\frac{9}{2}\gamma\frac{1}{t}\int_{0}^{t}r^{4}(s)ds\\ &+(\epsilon_{1}+\rho\epsilon_{2}\lambda_{r})\frac{1}{t}\widetilde{B}_{1}(t)+3\rho\epsilon_{2}\nu\frac{1}{t}\int_{0}^{t}r^{2}(s)d\widetilde{B}_{1}(s)\\ &+\sqrt{1-\rho^{2}}\epsilon_{2}\lambda_{r}\frac{1}{t}\widetilde{B}_{2}(t)+3\sqrt{1-\rho^{2}}\epsilon_{2}\nu\frac{1}{t}\int_{0}^{t}r^{2}(s)d\widetilde{B}_{2}(s). \end{split}$

(D.18)

Taking logarithm in (D.2) and dividing by $t$, we have

$\begin{split} \frac{1}{t}\log r(t)=&\frac{1}{t}\log r_{0}+\lambda_{r}+\nu\frac{1}{t}\int_{0}^{t}r^{2}(s)ds-\frac{1}{2t}\int_{0}^{t}(\epsilon_{1}+\rho\epsilon_{2}(\lambda_{r}+\nu r^{2}(s)))^{2}ds\\ &-\frac{1}{2}(1-\rho^{2})\epsilon_{2}^{2}\frac{1}{t}\int_{0}^{t}(\lambda_{r}+\nu r^{2}(s))^{2}ds+\frac{1}{t}\int_{0}^{t}(\epsilon_{1}+\rho\epsilon_{2}(\lambda_{r}+\nu r^{2}(s)))d\widetilde{B}_{1}(s)\\ &+\sqrt{1-\rho^{2}}\epsilon_{2}\frac{1}{t}\int_{0}^{t}(\lambda_{r}+\nu r^{2}(s))d\widetilde{B}_{2}(s)\\ =&\frac{1}{t}\log r_{0}+\lambda_{r}-\frac{\alpha}{2}+\bigg(\nu-\frac{\beta}{2}\bigg)\frac{1}{t}\int_{0}^{t}r^{2}(s)ds-\frac{\gamma}{2}\frac{1}{t}\int_{0}^{t}r^{4}(s)ds\\ &+(\epsilon_{1}+\rho\epsilon_{2}\lambda_{r})\frac{1}{t}\widetilde{B}_{1}(t)+\rho\epsilon_{2}\nu\frac{1}{t}\int_{0}^{t}r^{2}(s)d\widetilde{B}_{1}(s)\\ &+\sqrt{1-\rho^{2}}\epsilon_{2}\lambda_{r}\frac{1}{t}\widetilde{B}_{2}(t)+\sqrt{1-\rho^{2}}\epsilon_{2}\nu\frac{1}{t}\int_{0}^{t}r^{2}(s)d\widetilde{B}_{2}(s).\\ \end{split}$

(D.19)

By Doob's inequality, we know that $\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\widetilde{B}_{1}(t)=\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\widetilde{B}_{2}(t)=0$ almost surely. Since $r_{+}(\theta_{t}\omega)$ is ergodic and stationary process, letting $r (t)=r_{+}(\theta_{t}\omega)$ in (D.19) and $t\rightarrow\infty$, we have

$\begin{split} \underset{t\rightarrow\infty}{\lim}&\bigg(\bigg(\nu-\frac{\beta}{2}\bigg)\frac{1}{t}\int_{0}^{t}r^{2}_{+}(\theta_{s}\omega)ds-\frac{\gamma}{2t}\int_{0}^{t}r^{4}_{+}(\theta_{s}\omega)ds\\ &+\rho\epsilon_{2}\nu\frac{1}{t}\int_{0}^{t}r^{2}_{+}(\theta_{s}\omega)d\widetilde{B}_{1}(s)+\sqrt{1-\rho^{2}}\epsilon_{2}\nu\frac{1}{t}\int_{0}^{t}r^{2}_{+}(\theta_{s}\omega)d\widetilde{B}_{2}(s)\bigg)=\frac{\alpha}{2}-\lambda_{r} \end{split}$

(D.20)

almost surely. If $\lambda_{r} > \frac{\alpha}{2}$, associating with (D.18) and (D.20), we have

$\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\log D\Phi(t,r_{+})V=-2\bigg(\lambda_{r}-\frac{\alpha}{2}\bigg)-3\gamma\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\int_{0}^{t}r^{4}_{+}(\theta_{s}\omega)ds < 0$

(D.21)

almost surely, which implies the stability of the invariant measure $\delta_{r_{+}}$. At the same time, it is easy to check that

$\underset{t\rightarrow\infty}{\lim}\frac{1}{t}\log D\Phi(t,0)V=\lambda_{r}-\frac{\alpha}{2} > 0$

(D.22)

almost surely, which implies that $\delta_{0}$ is unstable. If $\lambda_{r} < \frac{\alpha}{2}$, then $\delta_{0}$ is stable. On the other hand, restricting $\Phi$ on $\mathbb{R}^{-}$ and following the arguments above, we obtain another ergodic invariant measure supporting on $\mathbb{R}^{-}$, which is also stable if $\lambda_{r} > \frac{\alpha}{2}$, $\gamma < \frac{3}{2}$. We conclude that if $\gamma < \frac{3}{2}$, system $\Phi$ occurs a pitchfork bifurcation at $\lambda_{r}=\frac{\alpha}{2}$.

---

Acknowledgments

We are grateful to the fund project-the Key Subject Funds of Guangzhou Financial Research (No.16GFR02B09) providing us with funding support.

---

Conflict of Interest

The author declares no conflict of interest in this paper.

---