Citation: James Bland, Gabriel da Silva. A detailed chemical kinetic model for pyrolysis of the lignin model compound chroman[J]. AIMS Environmental Science, 2014, 1(1): 12-25. doi: 10.3934/environsci.2013.1.12
| [1] | Vincent Carré, Sébastien Schramm, Frédéric Aubriet . Study of a complex environmental mixture by electrospray ionization and laser desorption ionization high resolution mass spectrometry: the cigarette smoke aerosol. AIMS Environmental Science, 2015, 2(3): 547-564. doi: 10.3934/environsci.2015.3.547 |
| [2] | Adi Setiawan, Ananda Fringki, M. Iqbal Hifzi, Shafira Riskina, Jalaluddin, Eddy Kurniawan, Burhanuddin . The effect of feedstock densification on the process and product properties of sugarcane leaves pyrolysis. AIMS Environmental Science, 2024, 11(6): 866-882. doi: 10.3934/environsci.2024043 |
| [3] | Qianlan Li, Qingdan Wu, Xiaochen Zheng, Pengfei Wang, Dongsheng Zou, Fen Liu, Zhihua Xiao . The conversion and migration behavior of phosphorus speciation during pyrolysis of different sludges. AIMS Environmental Science, 2024, 11(1): 1-20. doi: 10.3934/environsci.2024001 |
| [4] | B. Ravit, K. Cooper, B. Buckley, I. Yang, A. Deshpande . Organic compounds associated with microplastic pollutants in New Jersey, U.S.A. surface waters. AIMS Environmental Science, 2019, 6(6): 445-459. doi: 10.3934/environsci.2019.6.445 |
| [5] | Jennifer K. Costanza, Robert C. Abt, Alexa J. McKerrow, Jaime A. Collazo . Linking state-and-transition simulation and timber supply models for forest biomass production scenarios. AIMS Environmental Science, 2015, 2(2): 180-202. doi: 10.3934/environsci.2015.2.180 |
| [6] | B. Ravit, K. Cooper, G. Moreno, B. Buckley, I. Yang, A. Deshpande, S. Meola, D. Jones, A. Hsieh . Microplastics in urban New Jersey freshwaters: distribution, chemical identification, and biological affects. AIMS Environmental Science, 2017, 4(6): 809-826. doi: 10.3934/environsci.2017.6.809 |
| [7] | Premrudee Kanchanapiya, Supachai Songngam, Thanapol Tantisattayakul . The Adsorption of Perfluorooctanoic Acid on Coconut Shell Activated Carbons. AIMS Environmental Science, 2022, 9(2): 128-139. doi: 10.3934/environsci.2022010 |
| [8] | Rachel R. Sleeter, William Acevedo, Christopher E. Soulard, Benjamin M. Sleeter . Methods used to parameterize the spatially-explicit components of a state-and-transition simulation model. AIMS Environmental Science, 2015, 2(3): 668-693. doi: 10.3934/environsci.2015.3.668 |
| [9] | Li Ma, Likun Zhan, Qingdan Wu, Longcheng Li, Xiaochen Zheng, Zhihua Xiao, Jingchen Zou . Optimization of liquefaction process based on global meta-analysis and machine learning approach: Effect of process conditions and raw material selection on remaining ratio and bioavailability of heavy metals in biochar. AIMS Environmental Science, 2024, 11(3): 342-359. doi: 10.3934/environsci.2024016 |
| [10] | Kori Blankenship, Leonardo Frid, James L. Smith . A state-and-transition simulation modeling approach for estimating the historical range of variability. AIMS Environmental Science, 2015, 2(2): 253-268. doi: 10.3934/environsci.2015.2.253 |
Pyrolysis is a potentially viable technology for upgrading biomass to renewable liquid and gaseous fuels, as well as valuable commodity chemicals and solvents. With an increasing need for renewable energy resources, greater focus is currently being directed at modeling biomass pyrolysis. Modeling of such reaction schemes falls into two broad categories: (i) lumped models, where empirical fits are made to experimental results, not necessarily based on elementary reactions, and (ii) molecular-level models, which utilize large reaction networks along with the requisite fundamental kinetic and thermodynamic parameters [1, 2 , 3, 4, 5]. Molecular models are the more costly of the two to produce, but provide greater chemical insight into the pyrolysis process, along with improved extrapolation to conditions where experimental data does not exist.
The many components of biomass, and their heterogeneity, make the production of molecular-level kinetic models a complicated, expensive, and generally forbidding task. For woody biomass, we can separate the material into the discrete fractions of cellulose, hemicellulose, and lignin, which can then be described using a range of simplified model compounds [1, 2, 3, 4, 5]. Experimental and theoretical studies can provide the kinetic and thermodynamic properties required to predict the decomposition behavior of these model compounds, which can then be stitched together into large reaction networks. In this study we argue for a hybrid experimental/theoretical approach to the construction of molecular-level models for biomass pyrolysis. Theoretical gas kinetics methods, based upon ab initio computational chemistry and statistical reaction rate theory, can complement experimental studies by predicting rate coefficients, mechanisms, and products for reactions that may be difficult and/or costly to study in the laboratory. These theoretical techniques are now becoming widely adopted, and it is important that we begin to quantify their potential to contribute to the development of fundamental models of biomass pyrolysis.
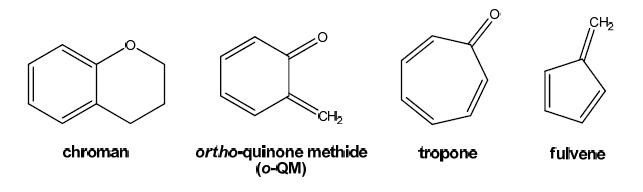
Chroman and ortho-quinone methide (o-QM), depicted in Scheme 1, are two of the many proposed model compounds for lignin [6], the oxygenated aromatic fraction of woody biomass that can account for around 20% of its mass. These compounds are also representative of functional groups encountered in low-rank coals and crude oils [7]. Chroman and o-QM are the targets of this study as their decomposition reactions have been studied both experimentally [6, 8, 9] and theoretically [10]. Furthermore, even though the chroman pyrolysis mechanism is thought to involve only a relatively small number of elementary reactions, there remain several outstanding aspects that would benefit from further study.
Scheme 1: Some important compounds from the present study.
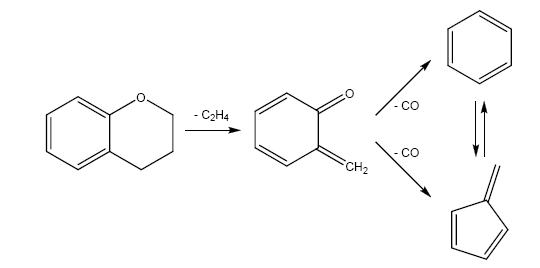
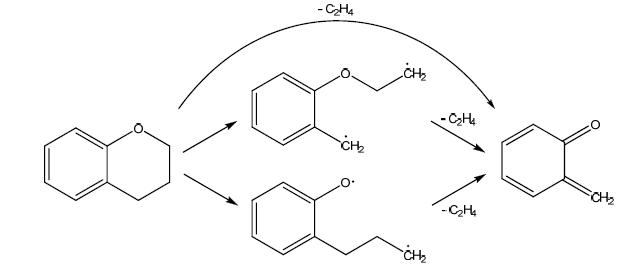
The main reaction steps thought to be involved in chroman pyrolysis are depicted in Scheme 2. Experimental studies reveal that the initial stage in chroman pyrolysis is decomposition to o-QM + ethene (C2H4), with activation energy of 263 kJ mol-1 [6]. This initial reaction step is not well understood, but is thought to involve either a concerted retro-Diels-Alder reaction or a step-wise biradical process, as shown in Scheme 3. The o-QM product of chroman decomposition is an important intermediate in lignin pyrolysis in its own right, formed for example in the thermal processing of o-methoxyphenol and its derivatives [11, 12]. Additionally, o-QM has been proposed as an intermediate in the combustion of alkylated aromatic hydrocarbons through oxidation of the o-methylphenyl radical [13, 14]. This radical can form in toluene combustion through abstraction of phenyl H atoms, and in o-xylene combustion via C—C dissociation or o-methylbenzyl radical oxidation [15, 16, 17, 18].
Scheme 2: Main reaction pathways in chroman pyrolysis.
Scheme 3: Concerted and step-wise mechanisms for decomposition of chroman.
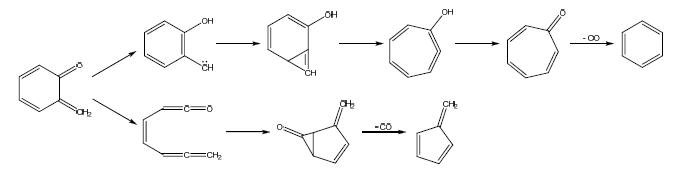
Once formed, o-QM can decompose to the C6H6 compounds benzene and fulvene (+ CO) [6, 19]. Experimentally, the overall activation energy for o-QM decomposition has been measured as 281 kJ mol-1 [6], and relatively high temperatures are therefore required to effect decomposition. Below 1000 K these experiments detected significant quantities of fulvene, but at higher temperatures benzene was the main decomposition product. A quantum chemical study of o-QM decomposition proposed the mechanism shown in Scheme 4, which accounts for the simultaneous formation of benzene (via a hydroxy-phenylcarbene intermediate) and fulvene (via a ring-opening intermediate that isomerizes to a bicyclic species). The overall activation energy was calculated as 298 kJ mol-1[6], where the benzene channel dominated at low temperatures and fulvene was the major product above around 1400 K. The isomerization of fulvene to benzene at these higher temperatures was proposed to explain the observations of Dorrestijn et al. [6]. In slow pyrolysis processes, where radicals are present, o-QM can also react with free H atoms or abstract H to form o-cresol, via either o-methylphenoxyl or o-hydroxybenzyl radical intermediates (here we are not concerned with the kinetics and mechanism of these radical processes). The presence of o-cresol in biomass pyrolysis residue points to o-QM as a key reaction intermediate, which is thought to play a crucial role in char formation [20].
Scheme 4: Proposed mechanism for decomposition of o-QM to benzene and fulvene (+ CO) [10].
This study aims to characterize the decomposition kinetics of chroman to the C6H6 species benzene and fulvene (+ CO) using a hybrid experimental/theoretical kinetic model. This model is then used to predict species profiles in the chroman decomposition process as a function of time and temperature, which are compared to experimental results. The aim of this study is to demonstrate the usefulness of theoretical methods in supplementing the experimental approach to constructing detailed molecular-level models for biomass pyrolysis, as well as to further explore the mechanism and kinetics of chroman and o-QM pyrolysis.
The decomposition of chroman to o-QM + C2H4 and the equilibrium reaction between fulvene and benzene have been studied using ab initio quantum chemical methods. All structures are optimized with the B3LYP/6-31G(2df, p) DFT model chemistry, with energies provided at the high-level composite G3SX level [21]. The G3SX method uses the B3LYP/6-31G(2df, p) structures, vibrational frequencies, and zero point energies, along with a series of single-point wavefunction theory energy calculations from HF theory through QCISD(T). Empirical scaling corrections are also incorporated into the final energy, along with spin-orbit corrections for the atoms. The G3SX method was chosen here for its accuracy in reproducing experimental thermochemical and kinetic properties [21, 22, 23]. All wave function theory and DFT calculations were performed using Gaussian 03 [24].
Thermochemical properties (ΔfH°298, S°298, CP(T)) are evaluated for stationary points in the chroman → o-QM + C2H4 reaction, and for the C6H6 species benzene and fulvene. Standard heats of formation (ΔfH°298, kJ mol-1) are calculated using atomization work reactions, as described recently [25]. Entropies and heat capacities are calculated according to standard principles of statistical mechanics, using B3LYP/6-31G(2df, p) optimized structures, vibrational frequencies, and moments of inertia.
High-pressure limit rate coefficients in the elementary chroman → o-QM + C2H4 reaction are calculated as a function of temperature from canonical transition state theory. Calculations were performed in ChemRate 1.5.2 [26], at temperatures between 300 and 2000 K. Calculated rate coefficients were fit to the Arrhenius equation or the modified three-parameter form of the Arrhenius equation k = A¢ Tnexp(-Ea/RT) in order to obtain the rate coefficient parameters Ea, A′, and n. All first-order rate coefficients reported in this study are in units of s-1, with A or A′Tn in s-1 and Ea in kJ mol-1.
This study seeks to replicate experimental results on chroman pyrolysis obtained using a flow reactor with online GC analysis [6, 9]. Assuming that plug flow conditions were obtained within the reactor, fluid elements at any position along the reactor (i. e. , in kinetic time) can be assumed homogeneous; the change in concentration with time of each species can thus be obtained by solving the system of ordinary differential equations (ODEs) that describes their formation and loss terms due to gas-phase chemical reactions only. By solving this system of ODEs over the residence time of the reactor we can then obtain the final composition. Experimental results were obtained under essentially isothermal conditions, with residence times between 2.9 s and 4.0 s. Our simulations are performed at constant temperature / constant volume conditions, using the average residence time of 3.45 s (note that varying the residence time between 2.9 s and 4.0 s changes the model results very little). For comparison to our model results, experimental data for composition versus temperature in chroman pyrolysis were graphically interpolated from the work of Dorrestijn et al. [6].
The system of reactions used to describe chroman pyrolysis is described later, but briefly it consists of: (i) irreversible chroman decomposition to o-QM + C2H4, (ii) irreversible o-QM decomposition to CO + benzene / fulvene, and (iii) reversible isomerization between fulvene and benzene. Radical processes, heterogeneous wall chemistry, and thermal decomposition of C2H4, benzene, and fulvene, are not considered here. The resultant system of ODEs, complete with all required rate coefficients, are solved numerically to obtain important species concentrations as a function of time. The numerical procedure uses a variable-order stiff ODE solver implemented in MATLAB, and is described in detail elsewhere [27].
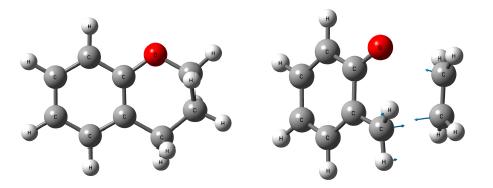
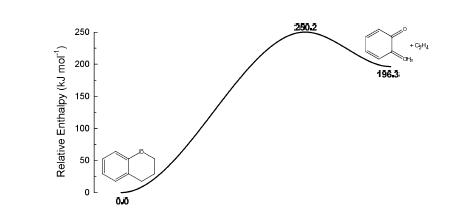
The decomposition of chroman to o-QM + C2H4 has been studied using the G3SX composite theoretical method. This reaction was found to proceed according to a concerted retro-Diels-Alder mechanism, via the transition state structure depicted in Figure 1 (which also displays displacement vectors for the imaginary vibrational frequency). An energy diagram for this mechanism is shown in Figure 2, constructed according to the theory of intersecting harmonic parabolic wells [28]. From Figure 2 we see that the standard enthalpy of activation for this dissociation reaction is 250 kJ mol-1, which is very similar to the experimental activation energy of Dorrestijn et al. [6]. The thermodynamic component of the barrier provides the largest impediment to reaction, with a relatively small barrier (53.9 kJ mol-1) for the reverse reaction between o-QM and C2H4.
Figure 1. Optimized structures for chroman (left) and its decomposition transition state (right). B3LYP/6-31G(2df, p) level.
Figure 2. Energy surface for the decomposition of chroman to o-QM + C2H4, at the G3SX level of theory.
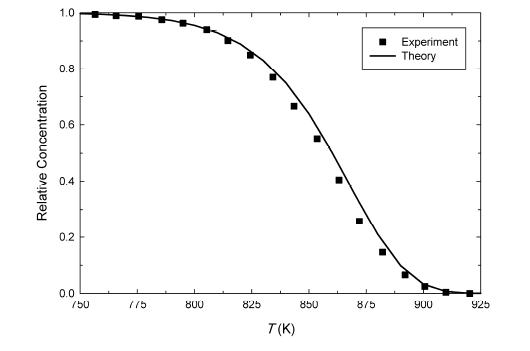
High-pressure limit rate coefficients for chroman decomposition have been calculated between 300 and 2000 K, and fit to the Arrhenius equation, providing a pre-exponential factor of 9.66×1014 s-1 and activation energy of 258.3 kJ mol-1. These values are in excellent agreement with the available experimental data, where the pre-exponential factor (2.00×1015 s-1) is slightly larger (i. e. , faster), compensating for the somewhat greater (i. e. , slower) activation energy (263 kJ mol-1). This is illustrated in Figure 3, where the experimental data for chroman decomposition measured between 750 K and 920 K is compared with simulated results using the theoretical rate coefficient expression. This figure demonstrates that the purely ab initio kinetic model for chroman decomposition can accurately describe the experimental data across the complete range of temperatures. The high level of agreement between the experimental and theoretical rate coefficient expressions provides strong support for the concerted retro-Diels-Alder mechanism proposed for chroman decomposition. The transition state structure for chroman decomposition is loose, with C···C distance of 2.16 Å and O···C distance of 2.29 Å . Displacement vectors illustrate that the main process occurring in the transition state is cleavage of the C—C bond, where O—C bond dissociation is almost complete. This loose transition state, dominated by C—C homolysis, provides a possible explanation for the high pre-exponential factor for this reaction, which was previously thought to be indicative of a step-wise biradical mechanism [29]. Rate coefficients have also been calculated in the reverse o-QM + C2H4 reaction, for the sake of posterity, and they are found to obey the expression k = 1.08×10-24T2.876exp(-6130/T) cm3 molecule-1 s-1 (in the high pressure limit from 300-2000 K).
Figure 3. Relative concentration of chroman from pyrolysis experiments between and 750 and 920 K, and predicted by a theoretical chemical kinetic model.
The final process for which rate coefficients are required is the isomerization of benzene to fulvene. The fulvene → benzene isomerization reaction has been studied by Gaynor et al. [30], and reverse rate coefficients can be obtained from K(T) according to the principle of microscopic reversibility. Thermochemical properties for benzene and fulvene have been calculated at the G3SX level and are listed here in Tables 1 and 2 (values for chroman are also included, for the sake of posterity). These results have been used to determine the equilibrium constant for the fulvene ↔ benzene isomerization process between 300 K and 2000 K, which are provided here in Table 3. Using our calculated K(T) values, and the experimental rate coefficient expression k(T) = 3.00×1013exp(－32716/T) s-1 for the fulvene to benzene rearrangement, we have calculated rate coefficients in the reverse process between 300 and 2000 K. Fitting these rate coefficients to the modified three-parameter Arrhenius expression we find k(T) = 4.00×1013T0.419exp(-48412/T) s-1. Note that the theoretical rate coefficient expression k(T) = 7.59×1013exp(－37170/T) s-1 has also been reported for the fulvene to benzene isomerization process [31]. There is a large difference between the theoretical and experimental activation energies for this isomerization reaction (37 kJ mol-1), and it has been previously suggested that the experimental data may be in error [31]. The kinetic model developed here provides us with an opportunity to reexamine this outstanding issue.
| ΔfH°298 (kJ mol-1) | S°298 (J mol-1 K-1) | ||
| benzene | 85.6 | 268.39 | |
| fulvene | 216.7 | 292.42 | |
| chroman | -92.1 | 360.04 |
DownLoad: CSV| 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 | |
| benzene | 80.99 | 110.88 | 136.48 | 157.17 | 187.57 | 208.67 | 241.00 | 255.74 |
| fulvene | 88.55 | 117.88 | 142.35 | 161.91 | 190.58 | 210.61 | 240.76 | 256.11 |
| chroman | 140.44 | 198.81 | 232.85 | 268.22 | 320.85 | 357.45 | 411.14 | 437.65 |
DownLoad: CSV| 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 |
| -21.547 | -15.831 | -12.383 | -10.074 | -7.174 | -5.425 | -3.084 | -1.91 |
DownLoad: CSVRate coefficient parameters for all reactions in the developed kinetic model are provided in Table 4. The chroman decomposition rate coefficient expression was derived by Dorrestijn et al. [6], using the experimental data that we are modeling here. For o-QM decomposition, the overall reaction rate is also that given by Dorrestijn et al. [6], but in order to describe formation of both benzene and fulvene the branching ratios for these two product sets calculated by da Silva and Bozzelli [9] are employed. Combining these rate coefficients for total decomposition and branching ratios to benzene + CO versus fulvene + CO we can calculate rate coefficients to both channels as a function of temperature (300-2000 K). Fitting these rate coefficients to the three-parameter form of the Arrhenius equation we obtain the rate coefficient expressions provided in Table 4. The rate coefficient fits require large negative values of n (and subsequently large values of A' to compensate), in order to describe the increasing contribution of fulvene with increasing temperature. Nevertheless, the two three-parameter rate coefficient expressions reproduce rate coefficients obtained via the single two-parameter experimental expression to within 2% at relevant temperatures. Finally, for the isomerization of fulvene to benzene the experimental rate coefficient expression of Gaynor et al. [30] is used, with reverse rate coefficients calculated here, as described above.
| A′ (s-1) | n (-) | Ea (kJ mol-1) | reference | |
| chroman → o-QM + C2H4 | 2.00×1015 | - | 263.0 | [6] |
| o-QM → benzene + CO | 2.38×1026 | -3.521 | 301.9 | [6], [10], this study |
| o-QM → fulvene + CO | 1.29×1029 | -3.800 | 352.9 | [6], [10], this study |
| fulvene → benzene | 3.00×1013 | - | 272.0 | [20] |
| benzene → fulvene | 4.00×1013 | 0.419 | 402.5 | [20], this study |
DownLoad: CSVExperimental results for the pyrolysis of chroman in a flow tube reactor at temperatures between 750 K and 1050 K, forming C6H6 products, have been simulated using the hybrid kinetic model described above. Experimental results for relative amounts of benzene + fulvene + 1-buten-3-yne are assumed to be equivalent to modeled total C6H6 products (benzene + fulvene).
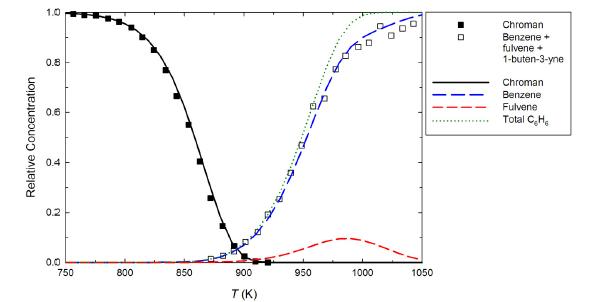
Concentrations of key species in the chroman pyrolysis process normalized against the initial chroman concentration, as predicted by the hybrid kinetic model, are shown in Figure 4. Not surprisingly, the model accurately describes the disappearance of chroman as a function of temperature. At temperatures above around 850 K the o-QM intermediate (not shown) begins to decompose, forming the C6H6 products benzene and fulvene, along with CO (model concentration of CO is equivalent to total C6H6). The model describes the formation of total C6H6 products (benzene, fulvene, and the fulvene decomposition product 1-buten-3-yne) accurately up to around 950 K. At higher temperatures the total concentration of C6H6 isomers is over-predicted, with the experimental results more-closely resembling the predicted benzene concentration. At temperatures of around 950 to 1000 K the formation of fulvene is expected to be significant; at lower temperatures fulvene is produced in minor amounts, while at higher temperatures it is predicted to isomerize to benzene. The reason for over-prediction of total C6H6 products is unclear, but could indicate that the experimentally determined activation energy for o-QM decomposition is slightly too large (by around 1 kJ mol-1). Alternatively, seeing as the predicted benzene concentration closely matches the measured benzene + fulvene + 1-buten-3-yne levels, this finding may indicate that the minor o-QM decomposition products (i. e. , those other than benzene) were not accurately quantified experimentally or that fulvene was decomposing to products that were unaccounted for.
Figure 4. Relative concentrations for key species in the pyrolysis of chroman, from experiment (dot points, ref. 3) and predicted by a hybrid experimental / theoretical kinetic model (solid lines).
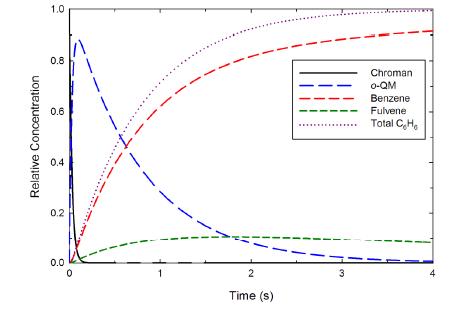
Figure 5 shows the time-evolution of species in chroman pyrolysis at 1000 K (a typical pyrolysis temperature). We find that chroman is removed within a fraction of a second, followed by slower decomposition of o-QM to both benzene and fulvene. At times longer than those shown, fulvene and benzene slowly achieve their equilibrium distribution.
Figure 5. Predicted species profiles versus time in chroman pyrolysis at 1000 K, using a hybrid experimental/theoretical kinetic model.
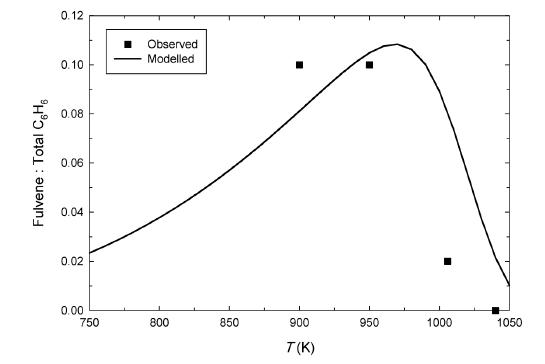
To further examine the role of fulvene in chroman pyrolysis, predicted ratios of fulvene to total C6H6 products are plotted in Figure 6, where they are compared with the available experimental data. The model shows that fulvene formation is kinetically limited at temperatures below about 950 K, above which the system approaches equilibrium. Experimentally, it was observed that fulvene accounted for around 10% of the o-QM decomposition products at 900 and 950, and 2% at 1006 K, with no fulvene detected at 1040 K and above. We find that the kinetic model can account for branching to fulvene relatively well at around 900-950 K. This suggests that the theoretically predicted branching ratio used in the kinetic model is relatively accurate, and therefore provides some support for the proposed mechanism. At higher temperatures the model also describes the decreased amounts of fulvene encountered experimentally, which suggests that the experimental rate coefficient expression for the isomerization of fulvene to benzene is accurate. In contrast, if the previously-obtained theoretical result for fulvene isomerization is used [31], predicted fulvene levels are dramatically over-predicted.
Figure 6. Ratio of fulvene to total C6H6 products in chroman pyrolysis, from experimental observations and kinetic modeling.
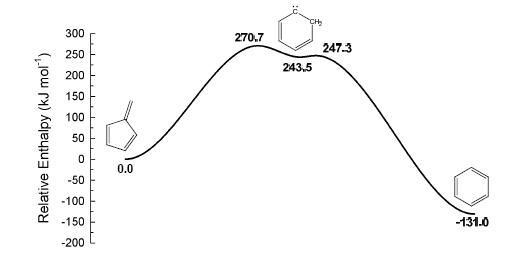
Fulvene is a product in many gas-phase reaction mechanisms, in addition to the more-stable and more commonly considered C6H6 isomer benzene [32, 33]. It is therefore critical that we understand the fate of fulvene in thermal systems, and can reconcile experimental observations with theoretical calculations. We have revisited the fulvene - benzene isomerization process theoretically, using the G3SX method. An energy surface for the isomerization of fulvene with benzene is shown in Figure 7. We find that the methylene group in fulvene initially adds to the five-membered ring to form a six-membered carbene product in a concerted reaction. The activation enthalpy for this initial reaction is 270.7 kJ mol-1, in excellent agreement with the overall experimental activation energy [30] but significantly smaller than the previously reported theoretical one [31]. Following this initial rearrangement, an intramolecular H atom shift takes place in the sparingly-stable six-membered carbene intermediate, with an almost negligible barrier. If we assume a single transition state model for this reaction, in which fulvene and benzene are directly connected by the highest-energy transition state structure, then we can approximate rate coefficients for the fulvene ↔ benzene isomerization reaction. Fitting high-pressure limit rate coefficients between 300 and 2000 K to the Arrhenius equation, we obtain the expression k = 3.12×1013exp(－32976/T) s-1 for the fulvene to benzene rearrangement, or k = 1.02×1015exp(－48941/T) s-1 in the reverse direction. These calculated rate coefficients for fulvene isomerization are in very good agreement with those measured experimentally, reconciling the previous discrepancy between experiment and theory.
Figure 7. Energy surface for the isomerization of fulvene to benzene, at the G3SX level of theory.
We have constructed and applied a hybrid experimental/theoretical detailed chemical kinetic model for the pyrolysis of chroman. In doing so, we have revealed important fundamental information about the kinetics and mechanism of chroman pyrolysis, but perhaps more importantly have demonstrated some of the ways in which high-level theoretical protocols (encompassing ab initio computational chemistry and statistical mechanics / reaction rate theory) can contribute to the development of molecular-level kinetic models for biomass pyrolysis. This study suggests that the thermal decomposition of chroman proceeds via a retro-Diels-Alder mechanism to o-QM + C2H4, with subsequent decomposition of the o-QM intermediate to both benzene and fulvene (+ CO). Isomerization of fulvene to benzene is found to be an important process in chroman pyrolysis; existing theoretical predictions of this reaction rate are found to be in error, although a new energy surface for this C6H6 isomerization is consistent with experiment. The hybrid model developed here can explain all prior observations in chroman pyrolysis with detailed knowledge of every elementary reaction step, and provides a strong case for combining experimental and theoretical methods in constructing molecular-level models for biomass pyrolysis.
Gabriel da Silva is grateful to the Australian Research Council for funding through the Future Fellowship (FT130101304) and Discovery Projects (DP110103889 and DP130100862) schemes.
All authors declare no conflicts of interest in this paper.
| [1] |
Hou Z, Bennett CA, Klein MT, et al. (2010) Approaches and software tools for modeling lignin pyrolysis. Energy Fuels 24: 58-67. doi: 10.1021/ef900488k
|
| [2] |
Klein MT, Virk PS (2008) Modeling of lignin thermolysis. Energy Fuels 22: 2175-2182. doi: 10.1021/ef800285f
|
| [3] |
Britt PF, Kidder MK, Buchanan AC (2007) Oxygen substituent effects in the pyrolysis of phenethyl phenyl ethers. Energy Fuels 21: 3102-3108. doi: 10.1021/ef700354y
|
| [4] | Beste A, Buchanan AC (2009) Computational study of bond dissociation enthalpies for lignin model compounds. Substituent effects in phenethyl phenyl ethers. J Org Chem 74: 2837-2841. |
| [5] |
Beste A, Buchanan AC (2011) Kinetic analysis of the phenyl-shift reaction in b-O-4 lignin model compounds: A computational study. J Org Chem 76: 2195-2203. doi: 10.1021/jo2000385
|
| [6] | Dorrestijn E, Pugin R, Nogales VC, et al. (1997) Thermal decomposition of chroman. Reactivity of o-quinone methide. J Org Chem 62: 4804-4810. |
| [7] |
Bao JP, Zhu CS, Ma AL (2009) The relationship between methylated chromans and maturity of organic matter in the source rocks from Jianghan hypersaline basin. Sci China Ser D – Earth Sci 52: 34-41. doi: 10.1007/s11430-009-5018-4
|
| [8] |
Paul GC, Gajewski JJ (1993) o-Benzoquinone methide: An intermediate in the gas-phase pyrolysis of chroman. J Org Chem 58: 5060-5062. doi: 10.1021/jo00071a013
|
| [9] |
Dorrestijn E, Mulder P (1998) The automation of a reactor flow system with online GC analysis. J Anal App Pyrolysis 44: 167-179. doi: 10.1016/S0165-2370(97)00084-3
|
| [10] | da Silva G, Bozzelli JW (2007) Quantum chemical study of the thermal decomposition of o-quinone methide (6-methylene-2,4-cyclohexadien-1-one). J Phys Chem A 111: 7987-7994. |
| [11] | Dorrestijn E, Mulder P (1999) The radical-induced decomposition of 2-methoxyphenol. J Chem Soc, Perkin Trans 2: 777-780. |
| [12] |
Britt PF, Buchanan AC, Cooney MJ, et al. (2000) Flash vacuum pyrolysis of methoxy-substituted lignin model compounds. J Org Chem 65: 1376-1389. doi: 10.1021/jo991479k
|
| [13] | da Silva G, Chen CC, Bozzelli JW (2007) Toluene combustion: Reaction paths, thermochemical properties, and kinetic analysis for the methylphenyl radical + O2 reaction. J Phys Chem A 111: 8663-8676. |
| [14] |
Prendergast MB, Cooper PA, Kirk BB, et al. (2013) Hydroxyl radical formation in the gas phase oxidation of distonic 2-methylphenyl radical cations. Phys Chem Chem Phys 15: 20577-20584. doi: 10.1039/c3cp53690d
|
| [15] |
da Silva G, Bozzelli JW (2009) Benzoxyl radical decomposition kinetics: Formation of benzaldehyde + H, phenyl + CH2O, and benzene + HCO. J Phys Chem A 113: 6979-6986. doi: 10.1021/jp902458d
|
| [16] |
da Silva G, Bozzelli JW (2009) Kinetic modeling of the benzyl + HO2 reaction. Proc Comb Inst 32: 287-294. doi: 10.1016/j.proci.2008.05.040
|
| [17] |
da Silva G, Hamdan MR, Bozzelli JW (2009) Oxidation of the benzyl radical: Mechanism, thermochemistry, and kinetics for the reactions of benzyl hydroperoxide. J Chem Theory Comput 5: 3185-3194. doi: 10.1021/ct900352f
|
| [18] |
da Silva G, Bozzelli JW (2010) On the reactivity of methylbenzenes. Comb Flame 157: 2175-2183. doi: 10.1016/j.combustflame.2010.06.001
|
| [19] |
Wentrup C, Muller P (1973) One-step synthesis of fulvene and fulvenallene: Thermolysis of alpha-coumaranone, phthalide, and benzocyclopropene. Tetrahedron Lett 14: 2915-2918. doi: 10.1016/S0040-4039(01)96281-1
|
| [20] |
Hosoya T, Kawamoto H, Saka S (2009) Role of methoxyl group in char formation from lignin-related compounds. J Anal Appl Pyrolysis 84: 79-83. doi: 10.1016/j.jaap.2008.10.024
|
| [21] |
Curtiss LA, Redfern PC, Raghavachari K, et al. (2001) Gaussian-3X (G3X) theory: Use of improved geometries, zero-point energies, and Hartree-Fock basis sets. J Chem Phys 114: 108-117. doi: 10.1063/1.1321305
|
| [22] |
Zheng J, Zhao Y, Truhlar DG (2009) The DBH24/08 database and its use to assess electornic structure model chemistries for chemical reaction barrier heights. J Chem Theory Comput 5: 808-821. doi: 10.1021/ct800568m
|
| [23] | da Silva G (2013) G3X-K theory: A composite theoretical method for thermochemical kinetics. Chem. Phys Lett chem Phys let 558: 109-113. |
| [24] | Frisch MJ, et al., Gaussian 03, Revision D.01, Gaussian, Inc., Wallingford CT, 2004. |
| [25] |
da Silva G, Moore EE, Bozzelli JW (2009) Decomposition of methylbenzyl radicals in the pyrolysis and oxidation of xylenes. J Phys Chem A 113: 10264-10278. doi: 10.1021/jp905722t
|
| [26] | Mokrushin V, Bedanov V, Tsang W, et al. (2006) ChemRate, Version 1.5.2, National Institute of Standards and Testing, Gaithersburg, MD. |
| [27] |
da Silva G, Dlugogorski BZ, Kennedy EM (2007) Elementary reaction step model of the N-nitrosation of ammonia. Int J Chem Kinet 39: 645-656. doi: 10.1002/kin.20280
|
| [28] |
da Silva G, Kennedy EM, Dlugogorski BZ (2007) Nucleophilic reactivity of aniline derivatives towards the nitroso group. J Phys Org Chem 20: 167-179. doi: 10.1002/poc.1142
|
| [29] | Schraa, GJ, Arends IWCE, Mulder P (1994) Thermal decomposition of 2,3-dihydro-1,4-benzodioxin and 1,2-dimethoxybenzene. J Chem Soc Perkin Trans 2: 189-197. |
| [30] |
Gaynor BJ, Gilbert RG, King KD, Harman PJ (1981) Kinetic study of the thermal isomerization of fulvene. Aust J Chem 34: 449-452. doi: 10.1071/CH9810449
|
| [31] |
Melius CF, Miller JA, Evleth EM (1992) Unimolecular reaction mechanisms involving C3H4, C4H4, and C6H6 hydrocarbon species. Symp (Int) Comb 24: 621-628. doi: 10.1016/S0082-0784(06)80076-7
|
| [32] | Miller JA, Klippenstein SJ (2003) The recombination of propargyl radicals and other reactions on a C6H6 potential. J Phys Chem A 107: 7783-7799. |
| [33] |
Soorkia S, Trevitt AJ, Selby TM, et al. (2010) Reaction of the C2H radical with 1-butyne (C4H6): Low-temperature kinetics and isomer-specific product detection. J Phys Chem A 114: 3340-3354. doi: 10.1021/jp911132r
|
| 1. | Samreen Hameed, Abhishek Sharma, Vishnu Pareek, Hongwei Wu, Yun Yu, A review on biomass pyrolysis models: Kinetic, network and mechanistic models, 2019, 123, 09619534, 104, 10.1016/j.biombioe.2019.02.008 | |
| 2. | Patrick Hemberger, Adam J. Trevitt, Thomas Gerber, Edward Ross, Gabriel da Silva, Isomer-Specific Product Detection of Gas-Phase Xylyl Radical Rearrangement and Decomposition Using VUV Synchrotron Photoionization, 2014, 118, 1089-5639, 3593, 10.1021/jp501117n | |
| 3. | Rubik Asatryan, Jason M. Hudzik, Joseph W. Bozzelli, Lavrent Khachatryan, Eli Ruckenstein, OH-Initiated Reactions of p-Coumaryl Alcohol Relevant to the Lignin Pyrolysis. Part I. Potential Energy Surface Analysis, 2019, 123, 1089-5639, 2570, 10.1021/acs.jpca.9b00185 | |
| 4. | Milad Narimani, Gabriel da Silva, Kalisadhan Mukherjee, Does ‘Dry Hit’ vaping of vitamin E acetate contribute to EVALI? Simulating toxic ketene formation during e-cigarette use, 2020, 15, 1932-6203, e0238140, 10.1371/journal.pone.0238140 | |
| 5. | Dijan SUPRAMONO, Eny KUSRINI, Haisa YUANA, Yield and Composition of Bio-oil from Co-Pyrolysis of Corn Cobs and Plastic Waste of HDPE in a Fixed Bed Reactor, 2016, 95, 0916-8753, 621, 10.3775/jie.95.621 | |
| 6. | Rubik Asatryan, Hayat Bennadji, Joseph W. Bozzelli, Eli Ruckenstein, Lavrent Khachatryan, Molecular Products and Fundamentally Based Reaction Pathways in the Gas-Phase Pyrolysis of the Lignin Model Compound p-Coumaryl Alcohol, 2017, 121, 1089-5639, 3352, 10.1021/acs.jpca.7b01656 | |
| 7. | Shanhui Zhao, Yonghao Luo, Multiscale Modeling of Lignocellulosic Biomass Thermochemical Conversion Technology: An Overview on the State-of-the-Art, 2020, 34, 0887-0624, 11867, 10.1021/acs.energyfuels.0c02247 | |
| 8. | Dan Wu, Donal F. O’Shea, Potential for release of pulmonary toxic ketene from vaping pyrolysis of vitamin E acetate, 2020, 117, 0027-8424, 6349, 10.1073/pnas.1920925117 | |
| 9. | Shan Zhu, Zhuofan Xiong, Chong-Wen Zhou, An extensive theoretical study on the thermochemistry of aromatic compounds: from electronic structure to group additivity values, 2022, 24, 1463-9076, 18582, 10.1039/D2CP01459A |
Figures(11) / Tables(4)
James Bland, Gabriel da Silva. A detailed chemical kinetic model for pyrolysis of the lignin model compound chroman[J]. AIMS Environmental Science, 2014, 1(1): 12-25. doi: 10.3934/environsci.2013.1.12
| ΔfH°298 (kJ mol-1) | S°298 (J mol-1 K-1) | ||
| benzene | 85.6 | 268.39 | |
| fulvene | 216.7 | 292.42 | |
| chroman | -92.1 | 360.04 |
DownLoad: CSV| 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 | |
| benzene | 80.99 | 110.88 | 136.48 | 157.17 | 187.57 | 208.67 | 241.00 | 255.74 |
| fulvene | 88.55 | 117.88 | 142.35 | 161.91 | 190.58 | 210.61 | 240.76 | 256.11 |
| chroman | 140.44 | 198.81 | 232.85 | 268.22 | 320.85 | 357.45 | 411.14 | 437.65 |
DownLoad: CSV| 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 |
| -21.547 | -15.831 | -12.383 | -10.074 | -7.174 | -5.425 | -3.084 | -1.91 |
DownLoad: CSV| A′ (s-1) | n (-) | Ea (kJ mol-1) | reference | |
| chroman → o-QM + C2H4 | 2.00×1015 | - | 263.0 | [6] |
| o-QM → benzene + CO | 2.38×1026 | -3.521 | 301.9 | [6], [10], this study |
| o-QM → fulvene + CO | 1.29×1029 | -3.800 | 352.9 | [6], [10], this study |
| fulvene → benzene | 3.00×1013 | - | 272.0 | [20] |
| benzene → fulvene | 4.00×1013 | 0.419 | 402.5 | [20], this study |
DownLoad: CSV| ΔfH°298 (kJ mol-1) | S°298 (J mol-1 K-1) | ||
| benzene | 85.6 | 268.39 | |
| fulvene | 216.7 | 292.42 | |
| chroman | -92.1 | 360.04 |
| 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 | |
| benzene | 80.99 | 110.88 | 136.48 | 157.17 | 187.57 | 208.67 | 241.00 | 255.74 |
| fulvene | 88.55 | 117.88 | 142.35 | 161.91 | 190.58 | 210.61 | 240.76 | 256.11 |
| chroman | 140.44 | 198.81 | 232.85 | 268.22 | 320.85 | 357.45 | 411.14 | 437.65 |
| 300 | 400 | 500 | 600 | 800 | 1000 | 1500 | 2000 |
| -21.547 | -15.831 | -12.383 | -10.074 | -7.174 | -5.425 | -3.084 | -1.91 |
| A′ (s-1) | n (-) | Ea (kJ mol-1) | reference | |
| chroman → o-QM + C2H4 | 2.00×1015 | - | 263.0 | [6] |
| o-QM → benzene + CO | 2.38×1026 | -3.521 | 301.9 | [6], [10], this study |
| o-QM → fulvene + CO | 1.29×1029 | -3.800 | 352.9 | [6], [10], this study |
| fulvene → benzene | 3.00×1013 | - | 272.0 | [20] |
| benzene → fulvene | 4.00×1013 | 0.419 | 402.5 | [20], this study |
