1. Introduction

In transmission networks, state estimation (SE) is a key function, since its results are used in fundamental network applications, such as optimal power flow, evaluation of available transfer capability, estimation of voltage and transient stability ^[1]. SE processes and filters real-time data (in terms of analogic measures, i.e., line flow, bus injection, voltage magnitude, or digital measures, i.e., switching devices status) available at the control centre of the transmission system to best estimate the current state of the network in order to provide dependable results to other network applications ^[2]. Typically, the aforementioned real-time applications are based on the knowledge of network topology, which is determined from the switching devices status ^[3]. Moreover, SE also uses topology to estimate the state and to identify bad data ^[1]. For these reasons, a great effort has been lavished to detect topology error in transmission systems ^{[2,3,4,5,6,7]}.

Traditionally, power distribution networks are either not observable or only partially observable ^[8], since they were excluded, in the past, from the deployment of communication infrastructures, automation, monitoring, and control systems ^[9]. Recently, the distribution system is facing a deeply transformation due, on the one hand, to the load growth and the proliferation of new "actors" (distributed generators, prosumers, electric vehicles, etc.) and, on the other hand, to the increasing demand for high quality, efficiency, security, reliability of energy supply, leading towards Smart Grid (SG) implementation ^[10]. In this complex scenario, SG implementation asks for the introduction of innovative paradigms, network control and management techniques, as well as planning and maintenance strategies that, in turn, ask for the integration of additional infrastructures, computational resources and data storage, for information exchange and processing, electrical vehicles, intelligent devices, network optimization procedures, remote control, automation and so on ^{[11,12,13,14,15,16,17]}. Many benefits are expected from this distribution network upgrade ^[18]; on the other hand, it also involves new problems related to distribution system vulnerability to cyber-physical attacks ^[19,20,21].

Many countermeasures against these attacks ^[22] require the knowledge of the network topology ^[23]. Nevertheless, many of the aforementioned applications are based on network topology too ^[9,24,25]. As said before, topology identification topic has been well investigated for transmission networks, differently from the distribution system, for which a traditional topology identification technique is not available at present. Of course, the distribution system upgrade could enable the Distribution System Operator (DSO) to adopt techniques similar to the ones used in transmission networks or even to develop new ones ^[25,26]. It is worth to highlight that these techniques are based on the assumption that the location of each link in the network is known, then "topology identification" means to determine if a link is open or closed ^{[2,3,4,5,6,7,25,26]}. A well-suited cyber attack can destroy such information and make network topology identification impossible, as well as make countermeasures and network applications impracticable. New techniques based on phasor measurement units (PMUs), specifically devised for distribution networks, could cope with this issue since they can provide information about power injection and voltage at the network nodes (therefore, the current absorbed from/supplied to the nodes is also known). In ^[9] the problem of reconstructing the topology of a portion of the distribution network using a dataset of voltage measurements is investigated, but it assumes that all power lines in the grid have the same inductance/resistance ratio and it neglects the information about power injections.

On the other hand, ^[23] performs a blind topology identification only by using power injection data at each bus, neglecting information about voltages, and it considers a simplified power flow, that is the linear DC power flow. In ^[8] both nodal measurement types are considered, but the algorithm is based on a linear coupled approximation for lossless AC power flow and the results are conditioned on a given assumption regarding correlations in power injections at the non-substation buses. In ^[27] network connectivity verification is proposed. It is based on an algorithm that neglects the presence of dispersed generation along the distribution network, since it assumes that voltage magnitude always decreases downstream along the feeder as it usually occurs in traditional passive distribution networks only.

The method proposed in this paper is able to identify the network topology after a critical event such as a cyber-physical attack or, more in general, when there is no information about the connections among the network nodes. It is able to exploit the knowledge of both nodal current and voltage measured by means of PMUs, and it is based on a full AC power flow avoiding all the limitations of the aforementioned methods.

Section Ⅱ describes the method proposed for identifying the network admittance matrix. Section Ⅲ describes the technique adopted to analyze the real part of the matrix in order to identify the network topology accounting for PMUs accuracy. Finally, section Ⅳ reports some numerical results.

---

2. Nodal admittance matrix identification by means of synchrophasors

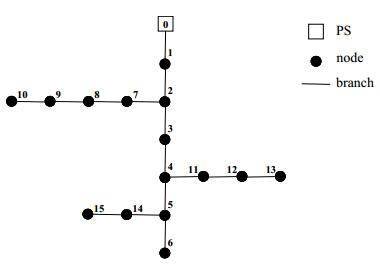
The one-line diagram of a feeder line of a three-phase, symmetrical, radial MV distribution network is considered. A graphic representation of the network is reported in Figure 1, where a node (filled point) is a network bus where customers and/or generators are connected, or a switching substation.

A branch (solid line) is a link that represents the electrical equipment connecting two nodes. The primary substation (PS) bus takes the labeled 0, the other nodes are sequentially numbered such that the ones from the PS to node i take a number lower than i. These nodes are said "upstream" from node i while node i is said "downstream" from them. From the graph theory a tree, as the radial network shown in Figure 1, has n branches and n+1 nodes. So, each branch can be numbered as the downstream node which it is connected to. The Kirchhoff's current law can be written for each node and the following equation in matrix form can be written ^[28]:

$[\bf Y][\bf V] = [\bf J]$

(1)

where:

[Y] size (n+1) × (n+1)—is the nodal admittance matrix, whose elements can be directly obtained by topological inspection according to the following rule:

(1) y_ii (self-admittance) is the sum of the admittances related to the branches that are connected to node i;

(2) y_ij (mutual admittance) is the negative of the sum of the admittances related to the common branches between nodes i and j;

[V] size (n+1) × 1—node voltages array;

[J] size (n+1) × 1—load/generator currents array; the real part of the current is considered positive when it is injected into the node ("absorbed" load current).

The equations in (1) are linear and complex. In the considered scenario, the elements in [Y] are unknown and do not change; the elements in [V] and [J] are the synchrophasors (Figure 2).

After a cyber attack that destroyed the stored information about the network structure, firstly, [Y] is found by exploiting a set of equation systems like the one in (1) and the PMUs information about nodal voltages and currents. Subsequently, the network admittance matrix is used to identify the network topology, thus restoring the missing information. In fact, the network admittance matrix encloses information about topology by construction, since y_ij equal to zero implies that there is not a link between node i and j, otherwise the nodes are connected to each other. On the other hand, in a real world application, such a term could differ from zero even when there is not a link between node i and j due to voltage and current data accuracy and numerical issues.

At the first step, the nodes belonging to a given feeder line, fl, have to be found to identify the nodal admittance related to fl itself. To this aim, the sending-end switch of the feeder line is set to "closed status", while the sending-end switches of the other feeder lines are set to "open status", to search for the nodes belonging to fl. More specifically, the nodes whose voltage syncrophasor differs from zero are the ones belonging to fl. Then another switch is set to "closed status", and the new nodes whose voltage syncrophasor differs from zero to another feeder line. For a given PS, this procedure stops when the nodes of its feeders are identified.

After that, the following method could be adopted to identify matrix [Y] of a feeder. Note that, to convert [Y] of Eq1 into an equivalent vector, in order to explicit the unknowns, let us define the row string vector operator, rs with size 1 × (n+1)², the column string vector operator, cs with size (n+1)² × 1, and the vectorization operator, ν (transposed row string vector) with size (n+1)² × 1, as follows ^[30]:

$^{\left[\mathbf{rs}\left( \mathbf{Y} \right) \right]\equiv \left[\begin{matrix} {{y}_{0, 0}}&{{y}_{0, 1}}&...&{{y}_{0, n}}&{{y}_{1, 0}}&{{y}_{1, 1}}&...&{{y}_{1, n}}&...&{{y}_{n, 0}}&{{y}_{n, 1}}&{}&{{y}_{n, n}} \\ \end{matrix} \right]}$

(2)

${{^{\left[\mathbf{cs}\left( \mathbf{Y} \right) \right]\equiv \left[\begin{matrix} {{y}_{0, 0}}&{{y}_{1, 0}}&...&{{y}_{n, 0}}&{{y}_{0, 1}}&{{y}_{1, 1}}&...&{{y}_{n, 1}}&...&{{y}_{0, n}}&{{y}_{1, n}}&{}&{{y}_{n, n}} \\ \end{matrix} \right]}}^{T}}$

(3)

$\left[{\bf{ \pmb{\mathsf{ ν}} }}(\mathbf{Y}) \right]\equiv {{\left[\mathbf{rs}(\mathbf{Y}) \right]}^{T}} = \left[\mathbf{cs}({{\mathbf{Y}}^{T}}) \right]$

(4)

Therefore, the following relations hold:

$\left[\mathbf{rs}\left( \mathbf{J} \right) \right] = \left[\mathbf{J} \right]{{\, }^{T}}$

(5)

$\left[\mathbf{cs}\left( \mathbf{J} \right) \right] = \left[\mathbf{J} \right]$

(6)

$\left[{\bf{ \pmb{\mathsf{ ν}} }}\left( \mathbf{J} \right) \right] = \left[\mathbf{J} \right]$

(7)

Moreover, the following relation is obtained by considering the standard multiplication of three matrices M₁, M₂, M₃ ^[30]:

$\left[{\bf{ \pmb{\mathsf{ ν}} }}({{\mathbf{M}}_{\mathbf{1}}}{{\mathbf{M}}_{\mathbf{2}}}{{\mathbf{M}}_{\mathbf{3}}}) \right] = \left[{{\mathbf{M}}_{\mathbf{1}}} \right]\otimes \left[{{\mathbf{M}}_{3}} \right]{{}^{T}}\left[v({{\mathbf{M}}_{2}}) \right]$

(8)

in which symbol ⊗ denotes the Kronecker product.

Note that, Eq 1 does not change by pre-multiplying it by the identity matrix [I] (with size n+1):

$\left[\mathbf{I} \right]\left[\mathbf{Y} \right]\left[\mathbf{V} \right] = \left[\mathbf{J} \right]$

(9)

Considering relations (7) and (8), this system of equations can be rewritten as follows:

$\overbrace{\left[\mathbf{I} \right]\otimes {{\left[\mathbf{V} \right]}^{T}}}^{\left( \text{n}+\text{1} \right)\text{ x }{{\left( \text{n}+\text{1} \right)}^{\text{2}}}}\ \left[{\bf{ \pmb{\mathsf{ ν}} }}(\mathbf{Y}) \right] = \left[\mathbf{J} \right]$

(10)

For example, when n = 2:

$\left[\begin{matrix} {{V}_{0}}&{{V}_{1}}&{{V}_{2}}&0&0&0&0&0&0 \\ 0&0&0&{{V}_{0}}&{{V}_{1}}&{{V}_{2}}&0&0&0 \\ 0&0&0&0&0&0&{{V}_{0}}&{{V}_{1}}&{{V}_{2}} \\ \end{matrix} \right]\left[\begin{matrix} {{y}_{0, 0}} \\ {{y}_{0, 1}} \\ {{y}_{0, 2}} \\ {{y}_{1, 0}} \\ {{y}_{1, 1}} \\ {{y}_{1, 2}} \\ {{y}_{2, 0}} \\ {{y}_{2, 1}} \\ {{y}_{2, 2}} \\ \end{matrix} \right] = \left[\begin{matrix} {{J}_{0}} \\ {{J}_{1}} \\ {{J}_{2}} \\ \end{matrix} \right]$

(11)

It is apparent that the number of equations is lower than the number of unknowns and, consequently, acquiring one set only of concurrent measures by means of the PMUs is not enough to calculate the elements of [Y]. Therefore, more equations are necessary, in other words many concurrent acquisitions at different instants must be performed. The first set of (n+1) equations is obtained by using in (10) the nodal measures acquired at time t₁ by means of the PMUs. The second set of equations is obtained thanks to the subsequent concurrent measures, acquired at time t₂, and so on.

Therefore, the following system of equations is obtained by considering (n+1) concurrent measures in (n+1) different instants:

$\begin{matrix} \left[\begin{matrix} \left[\mathbf{I} \right]\otimes \left[\mathbf{V}\left( {{t}_{1}} \right) \right]{{\, }^{T}} \\ \left[\mathbf{I} \right]\otimes \left[\mathbf{V}\left( {{t}_{2}} \right) \right]{{\, }^{T}} \\ ... \\ \left[\mathbf{I} \right]\otimes \left[\mathbf{V}\left( {{t}_{n+1}} \right) \right]{{\, }^{T}} \\ \end{matrix} \right]\left[{\bf{ \pmb{\mathsf{ ν}} }}(\mathbf{Y}) \right] = \\ ||| \\ \left[\mathbf{V}' \right] \\ \end{matrix}\begin{matrix} \left[\begin{matrix} \left[\mathbf{J}\left( {{t}_{1}} \right) \right] \\ \left[\mathbf{J}\left( {{t}_{2}} \right) \right] \\ ... \\ \left[\mathbf{J}\left( {{t}_{n+1}} \right) \right] \\ \end{matrix} \right] \\ ||| \\ \left[\mathbf{J}' \right] \\ \end{matrix}$

(12)

where:

$\begin{align} &\left[\mathbf{V}\left( \tau \right) \right] = \left[\begin{matrix} {{V}_{0}}\left( \tau \right)&{{V}_{1}}\left( \tau \right)&...&{{V}_{k}}\left( \tau \right)&...&{{V}_{n}}\left( \tau \right) \\ \end{matrix} \right]{{\ }^{T}} \\ &\left[\mathbf{J}\left( \tau \right) \right] = \left[\begin{matrix} {{J}_{0}}\left( \tau \right)&{{J}_{1}}\left( \tau \right)&...&{{J}_{k}}\left( \tau \right)&...&{{J}_{n}}\left( \tau \right) \\ \end{matrix} \right]{{\ }^{T}} \\ &with\quad \tau = {{t}_{1}}, \ {{t}_{2}}, \ ...\, {{t}_{n+1}}\ \\ \end{align}$

(13)

[V'], with size (n+1)² × (n+1)², is the coefficient matrix and [J'], with size (n+1)² × 1, is the known term array. System (12) is resolvable provided that the measures are not correlated among themselves, that is for each set of values measured at a given instant there must not exist a combination of the other sets that led to the same values in the considered set.

Note that, even though there are (n+1)² elements in [Y], the number of admittances to be found is (n+1)(n+2)/2 for symmetry reasons. Let us apply the reduced form of operator ν to account for this symmetric matrix ^[30]:

$^{\begin{smallmatrix} \left[\overline{{\bf{ \pmb{\mathsf{ ν}} }}}(\mathbf{Y}) \right]\equiv \left[\overbrace{\begin{matrix} {{y}_{0, 0}}&{{y}_{0, 1}}&...&{{y}_{0, n}} \\ \end{matrix}}^{\text{1 x }\left( \text{n}+\text{1} \right)}\quad \overbrace{\begin{matrix} {{y}_{1, 1}}&{{y}_{1, 2}}&...&{{y}_{1, n}} \\ \end{matrix}}^{\text{1 x n}}\quad ...\quad \overbrace{\begin{matrix} ...&... \\ \end{matrix}}^{\text{1 x }\left( \text{n}+\text{1-k} \right)}\quad ...\quad \overbrace{y{}_{n, n}}^{\text{1 x 1}} \right]{{\text{ }}^{T}} = \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \ \left[...\ {{y}_{rc}}\ ... \right]{{\ }^{T}}\quad \text{where }r = 0, 1, \, 2, \, ...n\text{ and }c = r, \, r+1, \, ...n \end{smallmatrix}}$

(14)

The reduced operator in (14) can be obtained from the one in (4) by applying the row deletion matrix, [D] with size 0.5(n+1)(n+2) × (n+1)²:

${{\left[\overline{{\bf{ \pmb{\mathsf{ ν}} }}}\left( \mathbf{Y} \right) \right]}^{{}}} = \mathbf{[D]}\ \ \left[{\bf{ \pmb{\mathsf{ ν}} }}\left( \mathbf{Y} \right) \right]$

(15)

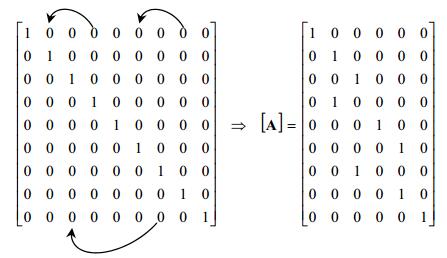
where [D] is obtained from a (n+1)²-dimensioned identity matrix by deleting some rows. More specifically, the i-th row of this matrix is deleted if the i-th element of [ν(Y)] is y_rc, with r greater than c. For example, when n = 2:

$\begin{align} &\left[\begin{matrix} 1&0&0&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0&0 \\ 0&0&1&0&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0&0 \\ 0&0&0&0&1&0&0&0&0 \\ 0&0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&0&1&0 \\ 0&0&0&0&0&0&0&0&1 \\ \end{matrix} \right]\quad \begin{matrix} {} \\ {} \\ {} \\ \leftrightarrow \\ {} \\ {} \\ \leftrightarrow \\ \leftrightarrow \\ {} \\ \end{matrix}\quad \left[\begin{matrix} {{y}_{0, 0}} \\ {{y}_{0, 1}} \\ {{y}_{0, 2}} \\ {{y}_{1, 0}} \\ {{y}_{1, 1}} \\ {{y}_{1, 2}} \\ {{y}_{2, 0}} \\ {{y}_{2, 1}} \\ {{y}_{2, 2}} \\ \end{matrix} \right] \\ &\ \Rightarrow \quad \left[\mathbf{D} \right] = \left[\begin{matrix} 1&0&0&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0&0 \\ 0&0&1&0&0&0&0&0&0 \\ 0&0&0&0&1&0&0&0&0 \\ 0&0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&0&0&0&1 \\ \end{matrix} \right] \\ \end{align}$

(16)

On the other hand, the operator ν can be obtained from the reduced one by applying the row addition matrix, [A]:

$\begin{align} &\left[{\bf{ \pmb{\mathsf{ ν}} }}\left( \mathbf{Y} \right) \right] = \left[\mathbf{A} \right]\ \left[\overline{{\bf{ \pmb{\mathsf{ ν}} }}}\left( \mathbf{Y} \right) \right] \\ &size\ of\ \left[\mathbf{A} \right]\quad {{\left( \text{n}+\text{1} \right)}^{\text{2}}}\text{x}\frac{\left( \text{n}+\text{1} \right)\left( \text{n}+\text{2} \right)}{2} \\ \end{align}$

(17)

where [A]—size (n+1)² × 0.5(n+1)(n+2) —is obtained from a (n+1)²-dimensioned identity matrix by deleting some columns and adding them to the others. More specifically, the i-th column of this matrix is deleted if the i-th element of [ν(Y)] is y_rc, with r greater than c, and the column deleted is added to the j-th column provided that the j-th element of [n(Y)] is y_cr. For example, when n = 2:

By applying to ν the row deletion and addition matrix in turn, the following relation holds:

$\left[{\bf{ \pmb{\mathsf{ ν}} }}\left( \mathbf{Y} \right) \right] = \mathbf{[A]}\ \left[\overline{{\bf{ \pmb{\mathsf{ ν}} }}}\left( \mathbf{Y} \right) \right] = \mathbf{[A][D]}\left[{\bf{ \pmb{\mathsf{ ν}} }}\left( \mathbf{Y} \right) \right]$

(19)

Therefore, the equation system in (12) can be rewritten as follows to account for symmetries:

$\left[\mathbf{V'} \right]\ \left[\mathbf{A} \right]\ \left[\overline{{\bf{ \pmb{\mathsf{ ν}} }}}\left( \mathbf{Y} \right) \right] = \left[\mathbf{J'} \right]$

(20)

and the sub-set of independent equations in the system is obtained by applying the row deletion matrix, provided that the measures are not correlated among themselves. Pre-multiplying the terms by the deletion matrix, the relations in (20) can be written as:

$\left[\mathbf{D} \right]\, \left[\mathbf{V'} \right]\ \left[\mathbf{A} \right]\ \left[\overline{{\bf{ \pmb{\mathsf{ ν}} }}}\left( \mathbf{Y} \right) \right] = \left[\mathbf{D} \right]\, \left[\mathbf{J'} \right]$

(21)

and the following reduced system of equations is obtained:

$\begin{align} &\left[\overline{\mathbf{V'}} \right]\ \left[\overline{{\bf{ \pmb{\mathsf{ ν}} }}}\left( \mathbf{Y} \right) \right] = \left[\overline{\mathbf{\Delta J'}} \right] \\ &with~~~~\left[\overline{\mathbf{V'}} \right] = \left[\mathbf{D} \right]\, \left[\mathbf{V'} \right]\ \left[\mathbf{A} \right] \\ &~~~~~~~~~~~~\left[\overline{\mathbf{\Delta J'}} \right] = \left[\mathbf{D} \right]\, \left[\mathbf{\Delta J'} \right] \\ \end{align}$

(22)

The reduced system of equations accounts for symmetries. On the one hand, it includes (n+1)(n+2) unknowns, that are the real and imaginary parts of the admittances; on the other hand, there are (n+1)(n+2) equations because each complex linear equation can be treated as two real linear equations.

---

3. Topology identification by using the nodal admittance matrix

The topology identification method proposed in this section is based on the use of the real part of [Y], i.e., the network conductance matrix [G]. The resulting information about the links in the network are stored in an array, [L], where a link between node i and j is represented by a number, k, which is computed as follows:

$\begin{align} &k = i\, \left( n+1 \right)+j\quad \\ &with\ i\in \left[0, n \right]\, , j\in \left[i+1, n \right] \\ \end{align}$

(23)

For example, when the network depicted in Figure 1 is considered, the link array [L] is:

$\left[\mathbf{L} \right] = \left\{ \begin{align} &\text{1, 18, 35, 39, 52, 69, 75, 86, 94, } \\ &\text{120,137,154,188,205,239} \\ \end{align} \right\}$

(24)

Information about the topology can be easily derived from [G] since the element at position (i, j) is equal to zero when there is not a link between nodes i and j, otherwise the nodes are connected to each other. On the other hand, in practical applications, such an element could differ from zero even when nodes i and j are not directly connected to each other due to PMUs accuracy and numerical issues. Therefore, a method to properly analyse the conductance matrix is proposed in the following. More specifically, such a method checks the sign of the mutual conductance values and compares some of them with the self-conductance. Moreover, it imposes radiality and connectivity constraints. The main steps of the proposed method are reported in Figure 3, where:

a.  ascend_order_position is a function that returns an array P such that:

$\begin{align} &G\left[i, P\left[p-1 \right] \right]<G\left[i, P\left[p \right] \right] \\ &with\quad p\in \left[1, n \right] \\ \end{align}$

(25)

when it is applied to (i, G);

b.  α is a negative number with magnitude lower than one;

c.  apply_eq23 is a function that applies equation 23 (even when j is lower than i+1);

d.  remove_duplicated_links is a function that removes from L each link k obtained for i higher than j;

e.  force_radiality is a function that removes as many links as necessary to avoid loops;

f.  force_connectivity is a function that adds as many links as it is necessary to avoid isolated set of nodes while keeping the radiality constraint satisfied.

The first link stored in [L] is the one connecting node 0 to the downstream node. Note that only one node is connected to node 0 when a specific feeder line is considered. Therefore, looking at the first row of [G], the column with the lowest value (that is the negative number with higher magnitude) indicates the node connected to 0 and, consequently, the related link is stored in [L] (see rows 3-4 in Figure 3).

When a generic node i is considered, the previous mechanism is firstly adopted. In other words, looking at the i-th row of [G], column j with the lowest value, i.e., G[i, P[1]], is found and the link between i and j is stored (see rows 7-8 in Figure 3). After that, the lowest one among the other elements in row i, i.e., G[i, P[2]], indicates another node that could be connected to i. The related link is stored in L provided that:

(1) the sum of the mutual-conductance magnitudes considered until that step does not exceed the self-conductance;

(2) the aforementioned lowest element is negative; and

(3) it has a magnitude comparable with the self-conductance (row 11 in Figure 3).

With reference to point 3, a coefficient α is used to establish if the element G[i, P[p]] can be considered exactly as "zero" although it actually differs from "zero". Such a difference is due to data accuracy and numerical issues.

After that, the next lowest value is considered and so on, as long as the three aforementioned conditions are satisfied (rows 11-15 in Figure 3). When the p-th lowest value is negative and it is comparable with the self-conductance (i.e., it satisfies conditions 2 and 3), but it hasn't been stored in [L] since the sum exceeds the self-conductance (i.e., it does not satisfy condition 1), the link is stored anyway if the addition of the mutual-conductance leads to a better approximation of the self-conductance (rows 16-19 in Figure 3).

A link between β and γ could be stored in [L] when i is equal to β, and the same link could be stored again in [L] when i is equal to γ. In other words, the same link is stored twice.

Conversely, a link between β and γ could be stored in [L] when i is equal to β, even though the link is supposed not to exist when i is equal to γ.

In both cases the link is added although in the first case it is more probable that the link actually exists. The function remove_duplicated_links erases the duplicates in the occurrence of the first case to avoid storing the same link twice (row 22 in Figure 3). Subsequently, two functions that, respectively, remove and add links to account for the topology constraints are executed (rows 23-24 in Figure 3).

The ability of the method to correctly identify each link is strongly dependent on the accuracy of [G], which in turn depends on the accuracy of the adopted PMUs, on the method adopted to solve the reduced system of Eq 22, and on the precision data type. Assuming a steady-state condition, a simple method to limit the impact of the PMUs' accuracy on the network conductance matrix is to repeat the acquisition of the set of nodal measures. More specifically, the values of V_i and I_i at time τ in Eq 13 can be obtained by averaging their measured values in the neighbourhood of τ.

For example, when R consecutive acquisitions are performed in the neighbourhood of a given time τ = t_m, the voltage at the i-th node is computed as:

$\begin{align} &{{V}_{i}}\left( {{t}_{m}} \right) = \frac{\sum\limits_{s = 1}^{R}{{{V}_{i}}\left( {{t}_{m}}+\left( s-\frac{R+1}{2} \right)\Delta \right)}}{r} \\ &with\ \ \ \ \ \ {{t}_{m-1}}<{{t}_{m}}-\left( \frac{r-1}{2} \right)\Delta \\ &\ \ \ \ \ \ \ \ \ \ \ \ {{t}_{m}}+\left( \frac{r-1}{2} \right)\Delta <{{t}_{m+1}} \\ \end{align}$

(26)

where Δ has to be a time interval small enough to ensure that the nodal voltages and currents do not change (accounting for R). The voltage (and current) values computed by using (26) are used in (22) to improve admittance matrix accuracy.

---

4. Case study

The method proposed to estimate the nodal admittance matrix and to identify the topology by using its real part has been implemented in a Java program. The program has been applied to the distribution network represented in Figure 1. The frequency has been assumed always equal to the nominal one and the coefficient α has been set to -0.05.

Firstly, it has been tested in case of no measurement error. To this aim, the line voltage magnitude at node 0 has been assumed always equal to 20 kV with phase 0, while 16 sets of simultaneous nodal voltages are randomly created for the other 15 nodes imposing that nodal voltage constraints are satisfied (±10% of nominal voltage as established by the standard EN 50160). After that, the simultaneous values of nodal currents are obtained by applying Eq 1 for each voltage set, so that each node could appear as a load point, a generation point or both. These sets of voltage and current values are provided to the program implementing the proposed method in order to emulate the concurrent measures of both voltage and current acquired in 16 different time instants.

The program has correctly evaluated the values of both real and imaginary parts of the nodal admittance matrix, as well as it has correctly identified the network topology (i.e., the identified link array is equal to the one in 24).

Subsequently, the program has been tested considering different PMUs accuracies. ANSI C 12.20 is the American national standard for electricity meter. The meters should satisfy Accuracy Class 5 (i.e., ±0.5%) at least, the best ones comply with Accuracy Class 2 (i.e., ±0.2%). Usually, PMU are very precise meters because their accuracy is less or equal to 0.1% ^[31].

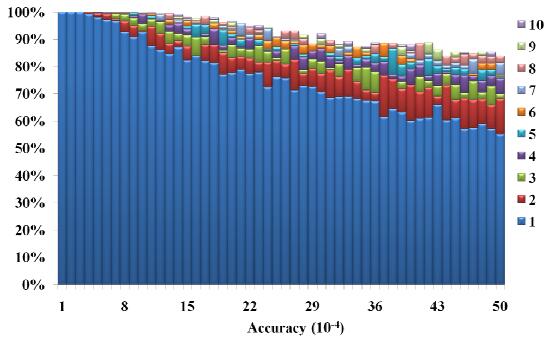
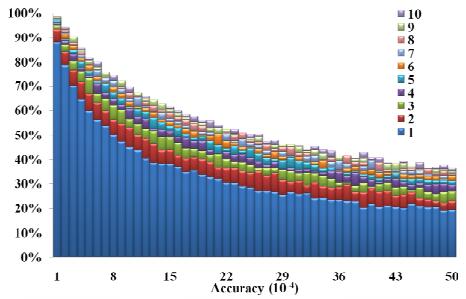
For a given accuracy, 100 tests have been performed and, for each test, the estimated link array has been compared with the correct one in order to compute the number of elements correctly identified. The average percentage of links correctly identified is reported in Figure 4 for different number of consecutive measures, with R∈[1, 10]. Therefore, 50,000 tests have been performed to evaluate the performance of the proposed approach on the 16-node test network of Figure 1.

In Figure 4, for a given PMUs' accuracy and R, the height of the related rectangle is equal to the average number of links correctly identified expressed in percentage.

Moreover, for a given PMUs' accuracy the rectangles are stacked one behind the other for increasing values of R. More specifically, the first one, i.e., the one in front, refers to R = 1, the second refers to R = 2 and so on. This implies that, for a given accuracy, the rectangle related to R = 2 is visible only when its height is greater than the one related to R = 1. Similarly, for example, a rectangle related to R = 5 is visible only if its height is greater than the ones related to r equal to 1, 2, 3 and 4.

Figure 4 shows that the proposed topology identification method always enable to identify correctly the network without any new acquisition (i.e., R = 1) when the PMUs' accuracy is less than 0.04%. Moreover, more than the 90% of the links are correctly identified when only one acquisition is performed (i.e., R = 1) and the PMUs' accuracy is less or equal to 0.1%. When r is greater than 8, the method always enables to identify correctly the network if the PMUs' accuracy is less or equal to 0.1%. Moreover, even when poor quality PMUs are considered, for example with accuracy up to 0.5% (i.e., Accuracy Class 5), at least the 90% of the links are correctly identified if many re-acquisitions are executed.

The main fact arising from the results is that few re-acquisitions are necessary to obtain correct results with typical PMU's accuracy. Finally, the worse the PMUs' accuracy the greater the advantage of performing re-acquisitions.

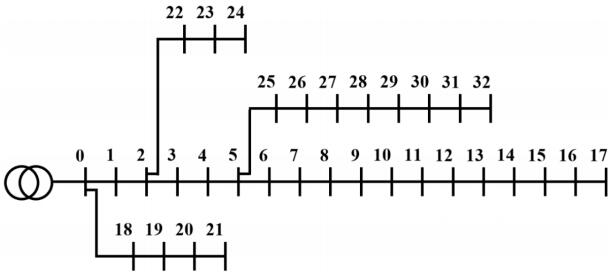
The program has also been applied to the IEEE test feeder with 33 nodes ^[32] represented in Figure 5. The link array [L] related to the network is the following:

$\left[\mathbf{L} \right] = \left\{ \begin{align} &\text{1, 35, 51, 69, 88,103,137,171,190,205, } \\ &\text{239,273,307,341,375,409,443,477, } \\ &\text{511,545,613,647,681,749,783,851, } \\ &\text{885,919,953,987, 1021, 1055} \\ \end{align} \right\}$

(27)

Similarly, to the previous test system, 33 sets of simultaneous nodal voltages are randomly created for node 1-32 then the related nodal currents are computed by applying Eq 1. These sets emulate the concurrent measures of both voltage and current acquired in 33 different time instants. When no measurement error is considered, that is the previous values are used without any modification, the proposed method has been able to find the correct value of all elements in the nodal admittance matrix. Moreover, the identified link array is equal to the one in 27 and hence the network topology has been correctly identified too. After that, 100 tests have been performed for each PMUs' accuracy as performed for the 16-node test system. More specifically, a slightly modification of the sets of concurrent measures has been done accordingly the given accuracy. The average percentage of links correctly identified is reported in Figure 6.

Comparing with the results obtained for the previous networks it is evident that the performance of the method degrades when the size of the network is doubled. On the other hand, the positive effect of performing more than one measure acquisition is very considerable even if the PMUs' accuracy is small, differently from the 16-node test system.

Therefore, the main fact arising from the tests performed on the 33-node test system is that the method proposed to estimate the nodal admittance matrix and to identify the topology still works but a large number of re-acquisitions are necessary to obtain sufficient or good results with typical PMU's accuracy.

---

5. Conclusion and future work

The basic theoretical aspects of the proposed method to identify the network topology using only voltage and current measures have been described. The method firstly uses these data to evaluate the elements of the nodal admittance matrix. It has been mathematically shown that to evaluate the value of all elements is necessary to concurrently measure both voltage and current at all nodes. Moreover, to this aim is also necessary to perform concurrent measures in different instants and the number of instants has to be equal to the number of nodes.

The second part of the method uses the real part of the nodal admittance matrix to identify the network topology. It checks the sign of the mutual conductance values and compares some of them with the self-conductance, and then it imposes radiality and connectivity constraints. The performance of the method to correctly identify each link strongly depends on the matrix accuracy and, in turn, on the accuracy of the adopted PMUs, on the numerical method adopted to solve the system of equations as well as on the precision of data storage.

The ability of the proposed method to identify the topology has been tested on two networks considering different PMUs' accuracy. When typical PMUs' accuracy is considered, the results show that the topology is always correctly identified in small networks. As the number of nodes increases, sometimes the topology is not correctly identified. However, a very great number of links in the network is correctly identified, and almost all if the measurements are very accurate.

Therefore, the proposed method is a promising starting point in the field of topology identification in distribution network subject to cyber attacks that have destroyed all information about network structure, historical data and so on. Further works will regard, by one hand, the development of very accurate PMUs, the research of the best method to solve the system of equations used for identify the nodal admittance matrix as well as the investigation of data storage precision on the performance. On the other hand, new features and improvement are necessary in the view of fully dependable topology identification in large networks.

---

Conflict of interest

The authors declare no conflict of interest in this paper.

---