Abbreviations: AMH: Adaptive Market Hypothesis; BRIC: Brazil, Russia, India, and China; CBOE: Chicago Board Options Exchange; CWT: Cross Wavelet Transform; GIIPS: Greece, Ireland, Italy, Portugal, and Spain; HMH: Heterogeneous Market Hypothesis; MODWT: Maximal Overlap Discrete Wavelet Transform; MWC: Multiple Wavelet Coherence; MWCC: Multiple Wavelet Cross-Correlation; PWC: Partial Wavelet Coherence; VIX: Volatility Index
1.
Introduction
In the history of financial markets, the peripheral European economies of Greece, Ireland, Italy, Portugal, and Spain (GIIPS) form the group of countries from the Eurozone that were severely affected by the European debt crisis that began nearing the end of 2009 (Apergis et al., 2016; Chiang et al., 2021; Flavin & Lagoa-varela, 2019, 2021). The economies of GIIPS have gained spate attention in recent strands of literature with almost a neglect to their stock markets. Not only did the Eurozone debt crisis leave its mark on bond markets, but it also affected other asset classes like stocks (Silva, 2021). Notably, stock markets' development and a vibrant economy are not independent of each other. Potent stock markets champion economic growth through the attraction of international capital flows and direct investments (Bossman, 2021; Bossman et al., 2022b).
The severe losses suffered by the GIIPS economies aroused the interest of scholars to investigate their interconnectedness, which is essential to policy and portfolio management (Agyei et al., 2021; Lee, 2021). The COVID-19 pandemic is one such health crisis that drives turbulent trading moments in financial markets, which could be likened, in part, to earlier crises characterized by systemic fundamentals (Aharon et al., 2021; Andrikopoulos et al., 2014; Riaz et al., 2020). Having found the overwhelming impact of these crises on various stock markets and macroeconomic variables (Silva, 2021), an essential element that has been ignored by the literature is the element of investor fear. While intrinsic factors are attributed to the high economic and financial integration of GIIPS markets (Andrikopoulos et al., 2014; Islam & Volkov, 2021), the role of external factors cannot be downplayed. As noted by (Owusu Junior et al., 2021a), aside from internal variables that contribute to the financial and economic fundamentals between economies, external factors are also a significant predictor of cross-economy conditions (Bouri et al., 2018), which explains why contagion may occur when stressed market conditions in one market (country) or a group of markets (countries) are transmitted to others. In such an instance, cross-market linkages are not attributed to interdependence (Forbes & Rigobon, 2001, 2002).
Empirically, uncertainties and fluctuations in the economic state of the US (especially the US stock market indices) on other stock markets have been established not only in normal trading periods, but also in crises periods (Karanasos et al., 2022; Owusu Junior et al., 2021a). The channel via which worsening macroeconomic performance affects the potency of stock markets is seen from the resultant contraction of exports and international capital flows. Consequently, international shocks such as those originating from the US economy could transmit to vulnerable economies, markets and/or regional blocs like the GIIPS. Notwithstanding, concerns about asymmetric volatility in the context of the US volatility index (VIX) and stock markets should not be overlooked. Investors' portfolio decisions are influenced by changes in market volatilities, which modify the risk-reward trade-off or their forecasts of future market performance (Owusu Junior et al., 2021a). Investors are incentivized to hedge against market volatility since increased volatility fails to stimulate investment opportunities (Owusu Junior et al., 2021b). To reiterate, periods of extreme volatility tend to coincide with stock market declines, which may erode investor confidence (Campbell & Hentschel, 1992).
Rapach et al. (2013) argue that stock returns in the United States are a good predictor of stock returns in both developed and developing nations. Recent studies have underscored the significant impact of uncertainties in the US on vibrant developing economies like Brazil, Russia, India, and China (i.e., BRIC) (Sarwar & Khan, 2017) and African markets (Adam, 2020). In the case of European market blocs, particularly GIIPS, the impact of uncertainties in the US has received a dearth of attention. We propose that the high integration among GIIPS markets arouses investor fear and cautions them against allocating funds to GIIPS stocks. A study that examines the integration of the GIIPS stock markets while evaluating investor sentiment and expectations has gotten virtually no attention. This is essential to GIIPS economies because potent stock markets attract capital flows and direct foreign investment.
Furthermore, in distinguishing between short-, medium-, and long-run investment horizons, assessments of the lead-lag comovement of GIIPS stock market returns and the implied VIX of the US, extending to the COVID-19 pandemic era, have gotten little or no attention. This is essential at this time owing to the systemic nature of the financial crisis in the era of the COVID-19 pandemic, which has not only affected numerous financial and commercial activities, but has also caused significant changes to investment trading and risk-mitigation strategies (Bossman, 2021). In this scenario, an empirical investigation that uncovers both the time and frequency domains of stock markets is beneficial (Kamaludin et al., 2021). Additionally, examining volatilities allows investors to modify their risk preferences and it is envisaged that regional analysis will aid investors in better understanding the geographical composition of volatility in their portfolios.
Time-frequency analysis is influenced by the inherently complex, non-linear, and asymmetric characteristics of financial time series (Bossman et al., 2022d), which has made the application of wavelet transforms predominant in evaluating the localised variations of power in time series (Agyei, 2022; Frimpong et al., 2021). The technique helps to focus on the comovements between two variables by eliminating appropriate influential factors at various periods and amalgamating partial correlation mechanisms. Given the non-linear character of time series, wavelet analysis is more appropriate in unveiling hidden and complex connections between variables as compared to other approaches that are strict on the linearity of time series (He et al., 2021). When used, wavelet preserves the features of time series (Umar et al., 2022a), hence, making it a suitable empirical methodology for this study, as we aim at analyzing the role of investor sentiment in the comovements between GIIPS stock markets' returns.
The last decade has witnessed different episodes of financial crises (e.g., Brexit and the US-China trade tension), but recovery from earlier episodes is yet to materialize with the GIIPS economies owing to their intense integration (Magnus & Blikstad, 2018). Assessments of the extent of integration and degree of interdependence between GIIPS stock markets across distinct time and investment scales make the application of the wavelet multiple techniques vital, in addition to the bi-wavelet. While the application of the bi-wavelet helps to reveal the correlation between paired series, multiple wavelet approaches are ideal for showing the coherence between several variables (Armah et al., 2022; Fernández-Macho, 2012).
Specifically, based on available matching data from 16/07/2013 to 03/02/2022, we undertake a pictorial examination—supported by Monte Carlo processes—of the multiscale interdependence of GIIPS whilst incorporating investor fear and sentiment through the bi-wavelet analysis. Complex investor behavior, as supported by the HMH of Muller et al. (1997) and the AMH of Lo (2004), results in market data characterized by noise (Bossman et al., 2022e). Overcoming this limitation warrants the application of multiscale analysis, which help reduce weak signals whilst true signals are preserved and further helps to reveal the relationships between variables across different frequencies representing investment horizons (Asafo-Adjei et al., 2021, 2022; Bossman & Agyei, 2022a, 2022b). On this premise, we employ the WMC and WMCC—in the frequency domain—to evaluate GIIPS markets' degree of integration and interdependencies across the short-, medium-, and long-term horizons.
The contributions of the study to the body of knowledge are threefold. First, we assess and report on the lead-lag dynamics—which are non-existent in the literature so far—between the GIIPS markets and the US VIX in both time and frequency paradigms. Second, in addition to the unconditioned interrelations between GIIPS stock returns and VIX, the conditional comovements between GIIPS markets are examined through partial wavelet analysis. Relative to a common interdependence, which is the US VIX, the comovements of GIIPS markets are investigated after eliminating mutual factors of interdependency (i.e., uncertainties in the US stock market). No study on GIIPS analyzes the integration of these markets at multiscale whilst controlling for investor fear.
Third, our analysis covers a dataset that extends to the recent key events (e.g., Brexit, the US-China trade tension, and the COVID-19 pandemic are notable events) in the history of financial markets. Time-frequency analysis covering these events could help ascertain whether interdependence persists for GIIPS economies across both calendar and intrinsic times. In tumult trading phases, we expect the comovement between investor sentiment (the US VIX) and GIIPS stock markets to follow a mutual pattern given that the markets are efficient (Fama, 1970). Due to the systemic market crisis brought on by the COVID-19 pandemic, there is a need to separately assess the efficiency of stock markets incorporating investor sentiment to reveal changes in market dynamics, if any. Resultantly, we deduce two sub-samples (pre-pandemic and pandemic), for which we report separate multiple correlations between GIIPS markets in the frequency-domain. This is relevant to investors that operate along timescales of short-, mid-, and long-term. Our study contributes to the recent strands of literature on GIIPS that assess the linkages between the markets and external macroeconomic factors (Riaz et al., 2020) and those that examine the influence of external variables on regional markets (Agyei et al., 2022b; Asafo-Adjei et al., 2022; Owusu Junior et al., 2021a).
In this study, the bi-wavelet analysis confirmed the strong comovements between GIIPS markets across diverse investment scales. The results confirm the negative connectedness between investor sentiment and GIIPS stock market returns at medium and low frequencies (i.e., medium- and long-term horizons), particularly between 2019 and 2022. The US VIX significantly drives GIIPS markets' connectedness. Furthermore, the sub-sample analysis suggests that the integration between GIIPS markets exacerbate during pandemics, but has the tendency to fall in prolonged tranquil markets.
The remainder of the paper is organized as follows. We present an extract of related works on GIIPS in Section 2. The datasets and methods employed are detailed in Section 3. The main results and practical implications are discussed in Section 4 while we conclude in Section 5.
2.
Literature review
In terms of literature on the peripheral European markets (i.e., GIIPS—Greece, Ireland, Italy, Portugal, and Spain), little attention has been paid to their stock markets. Most studies have focused on the larger European or Eurozone markets (Flavin & Lagoa-varela, 2019; Magnus & Blikstad, 2018; Reichlin, 2020). The focus of the earlier strands of literature paid attention to macroeconomic issues such as purchasing power parity, fiscal and external deficits (Ahmad & Aworinde, 2021; Algieri, 2013; Nazlioglu et al., 2021), demand exports (Algieri, 2014), volatility spillovers between currencies and stock markets (Andrikopoulos et al., 2014), dynamics in European sovereign bonds (de Vries & de Haan, 2016; Heryán & Ziegelbauer, 2016), the role of media sentiment and European markets (Andreas, 2020; Apergis et al., 2016; Beetsma et al., 2013; Dergiades et al., 2015; Kenourgios et al., 2020), factors that caused the sovereign debt crisis (Ewaida, 2017; Reichlin, 2020), integration of the entire European Monetary Union (Magnus & Blikstad, 2018), the stock-bond comovement (Flavin & Lagoa-varela, 2019; Lee, 2021), and the industrial, regional, and countrywide factors that influence stock returns (Chiang et al., 2021).
While the discourses of the extant studies are needed, they ought to be complemented by assessing the role of external factors on GIIPS economies, given their vulnerability to systemic shocks. This influences the current strands of literature on the GIIPS markets focusing on extrinsic factors such as the sovereign yield curve and credit ratings, and their impacts on GIIPS and international markets (Kenourgios et al., 2020; Riaz et al., 2020). In the context of asset allocation and portfolio management, little or no attention has been paid to the GIIPS economies despite the emergence of novel episodes of market crises such as the Brexit dialogues, the US-China trade tension, and the turbulent trading phases of the COVID-19 pandemic era. The role of external factors such as uncertainties in the US economy —on developing regional market blocs like BRIC has been established (Owusu Junior et al., 2021a). Notably, stock returns and uncertainties in the United States are good predictors of stock returns in both developed and developing nations (Rapach et al., 2013). To complement the recent literature that documents the significant impact of uncertainties in the US on vibrant regional blocs like BRIC (Sarwar & Khan, 2017) and Africa (Adam, 2020), as well as those works focused on the influence of external factors on GIIPS economies (Kenourgios et al., 2020; Riaz et al., 2020), we assess the role of investor sentiment in the cross-market linkages of GIIPS.
In the absence of any clear indications of the economic recovery of the GIIPS (Flavin & Lagoa-varela, 2019), empirical assessment of the role of external factors on the volatilities of GIIPS stock returns in a systemic crisis like the COVID-19 pandemic is timely. Furthermore, traditionally, equity investors are disposed to employing assets that are less or negatively correlated with stocks and the predominant asset employed is sovereign and corporate bonds. The latter attribute is known as a safe haven asset (Baur & Lucey, 2010), which need not exhibit a permanent and constant inverse relationship with stocks across all market conditions, but must bear such characteristics during stock market downturns (Flavin & Lagoa-varela, 2019). However, in the case of GIIPS which suffers from crises with detrimental impacts on bond markets (Silva, 2021), what other safe assets could be employed for equity-dominated portfolios? An empirical assessment of this situation warrants knowledge of the multiscale dynamics between these economies. We achieve this through the multiscale analysis of the dependencies between GIIPS stock market returns and investor fear.
3.
Data and methods
3.1. Data and description
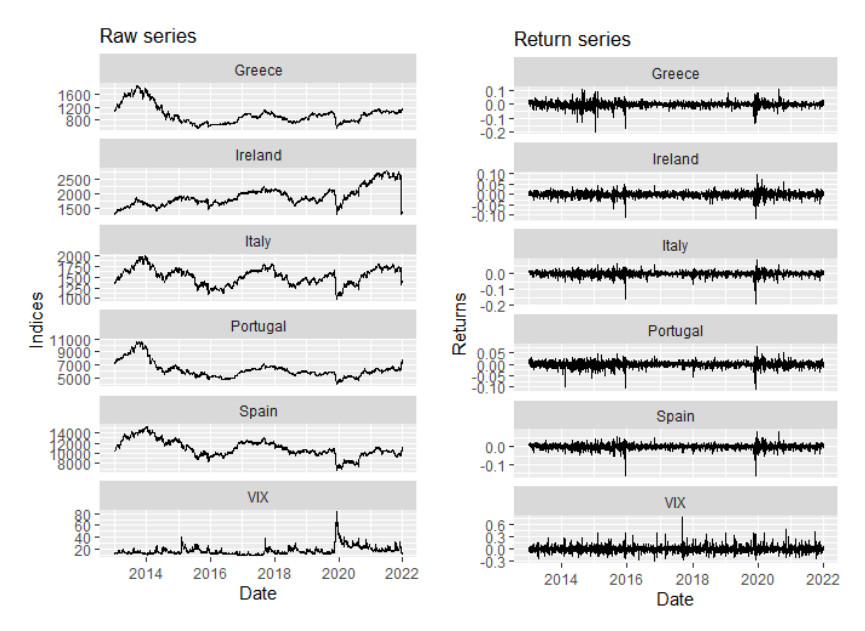
The data for the study comprises the daily stock market returns of the peripheral European markets, viz., Greece, Ireland, Italy, Portugal, and Spain, and the Chicago Board Options Exchange (CBOE) Volatility Index (VIX). All data cover the period 15/07/2013, to 03/02/2022 based on the availability of matching data for the studied stock markets. The sample period covers recent financial market actions such as Brexit, the US-China trade tension, and the COVID-19 pandemic era. A sum of 12,078 observations (i.e., 2003 each for 6 variables) were generated for estimations. Data on stock markets were supplied by EquityRT. Figure 1 shows a trajectory view of both raw and return series of all indices.
From the raw series in Figure 1, all stock indices depicted a downward trend in 2016 and 2020, with 2020 showing the sharpest decline and this represent the COVID-19-induced market stress (Bossman et al., 2022c; Owusu Junior et al., 2021b). The stock indices picked an upward trend after the sharp decline in 2020, suggesting that the markets bounced back in the latter months of the COVID-19 pandemic (Owusu Junior et al., 2021a). The US VIX index, conversely, picks a downward trajectory after a peak in 2020 and this communicates an inverse correlation between stock indices and investor sentiment. The negative association between stock market performance and investor anxiety conforms to the trajectories portrayed in Figure 1. Intuitively, the variables examined in this study are critical to investigate, particularly during times of uncertainty such as the COVID-19 pandemic era. By demonstrating volatility clustering, the log-return series supports the stylized facts of asset returns.
Table 1 presents the summary statistics of the daily stock returns for the GIIPS and the US VIX in Panel A while the pairwise unconditional correlations between GIIPS stock market returns and the US VIX are summarised in Panel B. The summary statistics for the pre-COVID-19 and COVID-19 periods are presented in Tables A1 and A2 in the Appendix.
The mean stock returns over the sample period is nearly zero for all series, all of which also reject normality, per the Normtest.W statistics. The leptokurtic behaviour of the data series is witnessed from the sample statistics. The Augmented Dickey-Fuller (ADF) and Phillips-Perron (PP) test statistics support the stationarity of the return series. The correlation coefficients corroborate the inverse relationship between stock market returns and investor fear.
3.2. Methodology
This section presents the methodological steps that allow us to evaluate the unconditional and conditional interdependencies, the lead-lag relationships, and the overall multiscale co-movements between stock markets returns of GIIPS.
Our approaches follow those from the works of (Agyei et al., 2022a) and (Bossman et al., 2022a), who could be consulted for comprehensive descriptions of the partial and multiple wavelet techniques. In the following, we present the steps involved in the bi-wavelet analysis.
The procedure for the bivariate wavelet technique follows the seminal works of Torrence and Compo (1998) and Torrence and Webster (1999). The approach has seen a recent propagation in the literature (Bossman et al., 2022a; Bossman et al., 2022d; Umar et al., 2021; Umar et al., 2022b). To arrive at the squared wavelet coherence, a wavelet transform is performed. This technique stems from a bivariate model grounded on a continuous wavelet transform (CWT) that can show various localized scales (Rua & Nunes, 2009).
A Morlet wavelet, as expressed in Equation (1), of Morlet et al. (1982) lays a foundation for the methodological steps:
The Morlet wavelet comprises a complex sine wave inside a Gaussian envelope. Following existing works, we resort to the CWT.
For the two distinct time series, $ a\left(t\right) $ and $ b\left(t\right) $, we follow (Torrence & Compo, 1998) to deduce the SWC between them from their various CWTs, $ {W}_{n}^{a}\left(u, s\right) $ and $ {W}_{n}^{b}\left(u, s\right) $, correspondingly as:
where $ u $ explains the location, $ s $ denotes scale, and a complex conjugate is denoted by *. With the help of the CWT, we can differentiate between various regions in the time-frequency domain, exhibiting the comovements between the two variables, even when they lack mutual strong power. Thus, across various wavelet scales, the CWT embodies the localized covariance between the analysed time series. As a result, a CWT metric close to 1 indicates a high coherence while a CWT metric of 0 denotes no significant coherence.
As per Torrence and Webster (1999), the comovement, denoted as the SWC, between the analyzed time series is defined as:
where $ S $ represents smoothing on the time-frequency spectrum. The parameters of the SWC can be defined as a correlation metric in the time-frequency spectrum, ranging between 1 and 0. Meanwhile, as opposed to the classical Pearson correlation metric, which ranges between 1 and −1, between two data arrays, the SWC metrics fall between 0 and 1 by default. Hence, it may fail to detect similar (positive) and opposing (negative) correlations.
For more insights into the dynamics of comovements and lead-lags between the analyzed pairs, the wavelet coherence phase difference is introduced as an underlying feature of the SWC. This is to facilitate correct distinctions between negative and positive comovements, as per Torrence and Compo (1998).
We can express the WCPD as:
where $ Im $ ($ Re $) represent imaginary (real) portions of the joint smoothed CWT.
When the analyzed data arrays have a null phase difference, they are said to have a perfect comovement. We adopt the standard graphical presentation of the results using heatmap panels. For each SWC heatmap, arrowheads signify phase connections between the named pair (i.e., either between investor sentiment (the VIX) and any member of the GIIPS—Greece, Ireland, Italy, Portugal, and Spain or between pairs of GIIPS stocks).
The analyzed paired variables may act in either out-phase (negative coherence) or in-phase (positive coherence) mode and these are shown by → and ← arrowheads, respectively. ↑ and ↓ arrowheads signify that the first (second) analyzed series leads the second (first), respectively by $ \mathrm{\pi }/2 $. Appreciating the above-mentioned guidelines helps to decipher the information portrayed by an arrowhead, despite its direction.
4.
Empirical results
The main results of the study are presented in his section. We first present the results from the time-frequency domain, which entails bi- and partial wavelets. In the former, the pairs are between GIIPS markets and each GIIPS market with the US VIX while in the latter, a covariate, the US VIX, is introduced to eliminate the effect of investor fear in the comovement between pairs of GIIPS stock market returns. Next to the time-frequency analysis, we present results on the frequency domain which includes the WMC and WMCC to assess the lead-lag potentials and degree of integration between all GIIPS markets in the midst of investor fear, the US VIX, across multiple scales delineating the short-, mid-, and long-term horizons.
4.1. Time-frequency analysis
The bi-wavelet technique is used to determine the degree and nature of causal relationships (i.e., either bi- or unidirectional) between two-time series variables in the time-frequency paradigm (Agyei, 2023; Asafo-Adjei et al., 2020). In both the time and frequency domains, this procedure would reveal the extent of comovements between two variables. Note that calendar time, reflecting the time-domain, is revealed on the horizontal axis, while intrinsic time, reflecting the frequency-domain is represented on the vertical axis. They constitute the time-frequency domain framework when put together in a scalogram. Gouhier et al. (2013) provided the statistical interpretations and analytic scripts.
4.1.1. Bi- and partial wavelets
The bi- and partial wavelets are presented in scalograms, from which we define the elements following the empirical literature (Agyei, 2022; Asafo-Adjei et al., 2021; Bossman et al., 2022a; Frimpong et al., 2021). Arrows pointing to the right (left) indicate when the first and second named series are "in-phase" (i.e., same direction movements) and "anti-phase" (i.e., movement in opposing directions), respectively. The first (second) named variable leads with right-pointing but up (left-pointing but down) arrows, whereas the second variable leads with left-pointing arrows upwards and right-pointing arrows downwards. The surface color and color palette signify the degree of interdependence between the given return series pair. Red or warmer colour denotes sections with significant interactions, whereas the blue or colder color denotes sections with lower interrelations between the paired series. Within (beyond) the bi-wavelet scalograms, the cone of influence signifies the region where wavelet interpretations fall within (outside) the 95% confidence interval and, hence, are significant (insignificant).
The bi- and partial wavelet coherence scalograms for the interrelations between pairs of GIIPS stock markets are shown in Figure 2. Scalograms on the left are for bi-wavelets with their corresponding partial wavelets on the right when investor fear (i.e., the US VIX) is introduced as a covariate series. Owing to the entrenched connectedness of the monetary system of GIIPS and the impervious GIIPS crisis (Magnus & Blikstad, 2018), it is not surprising that the bivariate coherence plots depict strong positive (in-phase) co-movements, especially in the long term, for all pairs and virtually for all periods between the pairs of Ireland-Spain, Italy-Spain, and Portugal-Spain. These are shown by the red- colored regions in the bi-wavelet coherence plots. A strong positive co-movement is depicted for all paired GIIPs markets across the long term (all timescales) during all market conditions (turbulent periods).
Turning to the partial wavelet coherence plots, from which investor fear is treated as a covariate, we find that the degree of connectedness (depicted by the hotter colors) between all pairs reduces. The implication is that uncertainties in the US economy, measured by the CBOE VIX, partly drive the co-movement between GIIPS stock markets. This finding supports the conclusion that investor sentiment driven by shocks from the US has significant influence on developed and vibrant developing economies (Sarwar & Khan, 2017). It is not surprising that a similar observation is documented by studies focused on other regions (Adam, 2020; Bossman et al., 2023; Owusu Junior et al., 2021a; Sarwar & Khan, 2017). Among African stock markets, for instance, Adam (2020) reports a significant effect of policy uncertainties from the US on African stock markets' returns. Owusu Junior et al. (2021a) also document significant interrelations between BRIC markets and the VIX.
It is instructive to note that despite the partial influence of the US VIX on the intraregional connectedness of GIIPS stock markets, which is more evident in pairs like Greece-Ireland, Greece-Italy, and Greece-Spain, the degree of connectedness seems resistant in the long term for some pairs (i.e., Ireland-Italy, Ireland-Spain, and Italy-Spain). The intuition is that idiosyncratic factors may play a role in the extent to which individuals and pairs of GIIPS stock markets are affected by uncertainties from the US stock market.
To substantiate the partial role of investor fear in the comovements of GIIPS stock markets, we provide a separate analysis of the interrelations between individual GIIPS markets and GIIPS in Figure 3. This provides insights into how each of the markets is connected with the uncertainties from the US, as quantified by investor fear, the US VIX.
The bivariate coherence plots between GIIPS markets and investor fear is either negative or VIX-driven across all years and timescales, as depicted by the left-pointing and left-pointing but up arrows, respectively. These co-movements are predominant in crisis periods such as in 2016/17 and 2019–2022. These periods map to significant events in the history of financial markets. for instance, 2016/17 was characterized by the Brexit dialogues and vote, and 2019–2022 by the US-China trade tension and the COVID-19 pandemic. These events, which result in turbulent trading environments that intensify cross-market co-movements (Bosman, 2021; Bossman et al., 2022b; Owusu Junior et al., 2021a).
The unsurprising negative relationship between GIIPS markets and investor fear (the VIX) corroborates our preliminary observation from their unconditional correlations. Moreover, the VIX-driven co-movements further substantiate the results from the partial wavelet coherence. From the coherence plots between individual GIIPS markets and the VIX, we find no evidence that suggests that any of the GIIPS markets drives its relationship with the VIX. Therefore, we document that the strong co-movement between paired GIIPS markets partly results from investor fear. Similar dynamics between investor sentiment and the stock returns from developing market blocs like BRIC (Bouri et al., 2018; Owusu Junior et al., 2021a) are documented.
4.2. Frequency-domain analysis
A further substantiation of the time-frequency dynamics of GIIPS markets and investor sentiment leads us to the frequency domain, where we analyze the bi- and multi-variate correlations between GIIPS markets and investor fear. The wavelet bivariate correlations are briefly presented followed by the wavelet multiple correlations and cross-correlations across differing investment horizons.
4.2.1. Wavelet bivariate correlations matrix
We analyze a 7-scale (6-scale for the COVID-19 sample) pairwise contemporary correlations (see Figure 4) with codes C1-C6, for Greece, Ireland, Italy, Portugal, Spain, and VIX, respectively. To retrieve the wavelet paired correlation coefficients, the combinations (scales or frequencies) are presented on the horizontal (vertical) axis. Moving from left to right, weaker correlations for GIIPS and investor expectations and fear (i.e., the VIX) are observed.
Notably, the results from the wavelet bivariate correlations matrix in Figure 4a (full sample) do not deviate from those portrayed by the bivariate coherence analysis. With symmetrical correlations ranging between 0.88 and 0.93, Italy and Spain serve as the strongest correlated pair across all frequencies. Thus, at all wavelet scales, among GIIPS markets, Italy-Spain exhibits the strongest positive correlation, which is followed by the pairs of Portugal-Spain, Ireland-Spain, Italy-Portugal, Ireland-Italy, Ireland-Portugal, Greece-Spain, Greece-Italy, Greece-Portugal, and Greece-Ireland. The high co-movements between pairs of GIIPS stock markets across all time scales are an indication that portfolios constructed with all GIIPS assets are suboptimal since portfolios with highly impervious correlated assets achieve no diversification, hedge, and safe haven benefits during calm or turbulent trading periods (Baur & Lucey, 2010). Momentarily, however, for risk management, allocations could be made by simply choosing any of the GIIPS stock markets because they exhibit similar co-movements.
It is instructive to note that with the inclusion of investor expectations and fear, measured by the US VIX, we observe negative correlations between the US VIX and each of the GIIPS markets. The implication is that, when contained in the same portfolio, volatilities from GIIPS stocks could be hedged against using the US VIX. This corroborates the conclusions of Owusu Junior et al. (2021a) and Shahzad et al. (2022) that the US VIX serves as a hedge for some equity markets. The results from the pre-pandemic and pandemic sub-samples (Figure 4a and 4b, respectively) reveal similar results with one peculiarity. The correlations between paired GIIPS markets are high across all scales of either sample but in lower (higher) magnitudes for the pre-COVID-19 (COVID-19) pandemic sample. This is intuitively given that cross-market correlations are expected to intensify during turbulent periods (Umar et al., 2023). This substantiates our assertion that investor sentiments, measured by the US VIX, serve as a hedging instrument for GIIPS stocks.
4.2.2. Wavelet multiple correlation (WMCC)
The WMC of GIIPS stock markets' returns while incorporating investor expectations and fear is pictorially denoted in Figure 5 and supported numerically by the results in Table 2. Across the short-to-long term dynamics, these results—based on MODWT's frequency localization—emphasize the degree of integration among the studied stock markets (Armah et al., 2022; Fernández-Macho, 2012). The lead/lag variable is, although not revealed, the overall interrelationships between the VIX and the GIIPS stocks are described by the findings. We find that GIIPS stock markets are generally more integrated, as established in the previous analysis. Thus, although the WMC results confirm prior ones, there are significant revelations that need to be highlighted.
The WMCs across timescales in Figure 4a (full sample) indicate a rising trajectory at higher (lower) scales (frequencies), which shows a perfect aggregation of those in Figures 5b (pre-COVID-19 pandemic sample) and 5c (COVID-19 pandemic sample). Specifically, in the pre-pandemic sample, the WMC picks a mild decreasing trend at higher (lower) scales (frequencies) whereas in the COVID-19 sample, we find the opposite, a steeper increasing trend at higher (lower) scales (frequencies). This explains why in the aggregate, the full sample (Figure 5a), a rising trend of WMC is observable. Backed by empirical and theoretical literature, our results show strong convergence between GIIPS markets during crisis periods although in prolonged tranquil periods, divergence could be triggered at higher (lower) scales (frequencies). The high integration of GIIPS even in normal trading periods is mainly due to the resistant GIIPS crisis (Magnus & Blikstad, 2018). These pictorial deductions are confirmed by the numerical findings in Table 2.
As summarised in Table 2, in the full sample, a 96.17% WMC coefficient (88.59% at the lower panel and 98.75% at the upper panel) is revealed. The WMC reduces (rises) to 88.36% (99.99%) in the pre-COVID-19 (COVID-19) sample within the quarterly-to-biannual scale (i.e., long-term frequency/horizon). Therefore, averagely, at scale 64 (i.e., quarterly) interdependence, over 96% (88%) of the daily returns of any of the GIIPS stock markets is explained by the remaining variables in the full (pre-COVID-19) period. In the peak of the COVID-19 era, the WMC is nearly a perfect one, which is 99.999% and achievable at scale 32 of interdependency. This is not surprising owing to the fundamentals of GIIPS markets (Magnus & Blikstad, 2018).
4.2.3. Wavelet multiple cross-correlation
Figure 6 and Table 3 show pictorial and numerical results, respectively, on the WMCC for GIIPS markets amid investor expectations and fear. We use these results to confirm the lead/lag market or variable across various wavelet scales. Negative (positive) values signify a lead (lag). An absence of a lead/lag market is defined by zero and localisations are portrayed by dashed lines. Note that Figure 7 (see Appendix) shows the segmented representation of the heatmap in Figure 6 using wavelets multiple cross-correlations classical plots. Thus, Figure 7 confirms the listed series on a particular scale in Figure 6.
Based on the full sample, the stock market returns of Spain tend to be the potential lead or lag series (at lag 0 but lag 1 for scale 16~32) across all scales except for scale 64 (quarterly) of interdependency, where Irish stocks take on the actual lag variable (at lag 2) in the 32~64 (monthly-to-quarterly) scale. This suggests that, in the short-to-medium-term, concerning the performance of GIIPS stock markets, Spanish stocks are the first or last to either respond to or recover from shocks relative to the remaining GIIPS markets. In the medium (long) term, among the peripheral European markets, Spanish (Irish) stocks lag all other GIIPS markets, implying that the Spanish (Irish) stock market is the last to recover from or experience shocks. In the pre-COVID-19 era, we find Spain to be the potential and actual lead/lag stock market among the GIIPS.
Over the COVID-19 period, the short- and medium-terms are dominated by the Spanish and Italian stock markets but at zero lags except for Spain at scale 16 of interdependency which shows a main lag (at lag 1). The Irish stock market leads (at lag −8) at scale 32 of interdependency. The implication is that during turbulent periods, we expect Irish markets to be the first to recover, as they become the first to be affected by shocks among GIIPS. This could be substantiated by the fact that among the GIIPS markets, the Irish market is the first to implement long-term economic recovery policies (Magnus & Blikstad, 2018).
Note that the lead-lag dynamics for specific lead/lag markets among GIIPS across the various scales are better portrayed in the classical WMCC plots (see Figure 7 in the Appendix). The lead/lag series across the various scales are substantiated by the segmented results of the classical WMCC plots in Figure 7. At zero lags, we find an indication of symmetry (zero skewness) (e.g., as shown in Levels 1–5 of Figure 7a). The localisations are in black traces with red upper and lower confidence bounds. A named series is the lead/lag series (market) that maximizes the multiple correlations against a linear combination of the remaining markets. The results suggest that the correlation between all the GIIPS markets is generally high and at the same time, increases with frequencies or time horizons, revealing no significant diversification, safe haven, or hedge benefits for all timescale investors. However, the shocks from these markets could be hedged by the US VIX at strategic timescales, depending on the specific GIIPS market combined with the VIX. This is viable since investor fear, quantified by the VIX, was neither a lead nor lag variable with its cross-combinations with GIIPS markets.
4.3. Practical implications of empirical findings
We summarise the practicality and economic intuitions of our findings as follows. Owing to the fundamental factors that exist between GIIPS markets, we note that cross-market linkages, both pairwise and overall, are generally higher across all periods. However, we draw insights from the sub-sample analysis, which suggests that in extended periods of tranquil trading environments, the overall comovement between GIIPS stock markets tends to pick a decreasing trend. With proper recovery policies, investors could, thus, expect a falling degree of connectedness between GIIPS assets. While this may be unattractive to short-term investors, optimists and long-term investors could place reliance on this to take advantage of diversification with less correlated GIIPS stocks (Baur & Lucey, 2010) in long periods of average market conditions. Notably, due to the similarities in comovements, any of the GIIPS stocks could be selected for inclusion in portfolios.
Our findings reveal negative comovements between GIIPS and VIX, implying that the volatilities in GIIPS markets could be hedged against using the US VIX. In the coherence plots, investor expectations and fear, quantified by the VIX, are either negatively related to individual GIIPS stocks or drive its co-movement to each GIIPS market. Notably, our expectation that the comovement between investor sentiment (the US VIX) and GIIPS stock markets would follow a mutual pattern given that the markets are efficient is met. Intuitively, investors trading on arbitrage may not succeed owing to the relative efficiency of the markets. Notwithstanding, the resistant cross-market linkages between pairs of GIIPS stock markets are induced by investor sentiments and, hence, for portfolios containing any of the GIIPS stocks, investors could allocate investable funds into the US VIX to hedge against the shocks that are transmitted by GIIPS. This supports the findings of recent works like Shahzad et al. (2022) and Owusu Junior (2021a), who find the VIX as a hedging instrument for stocks in different contexts.
In crisis periods, where spillovers are high between markets (Owusu Junior et al., 2021b), GIIPS markets are nearly perfectly integrated. Although the US VIX proves a viable hedge across various timescales (frequencies), the degree of economic and financial market integration of GIIPS suggests that, in such tumult periods, the role of the US VIX as a hedge or safe haven may depend on specific pairs of GIIPS stocks due to the idiosyncratic shocks propagated by individual markets. Notwithstanding, we divulge that consistent with the full sample, from the COVID-19 pandemic sample, the Irish stock market could be the first to recover from market shocks, particularly in the long term, i.e., lower (higher) frequency (scales). This implies that the efficacy of recent economic recovery policies initiated by Ireland may take time to manifest in their stock markets and the delay of other GIIPS countries in implementing economic recovery policies may intensify the resistance to the overall connectedness of GIIPS markets (Magnus & Blikstad, 2018).
5.
Conclusions
The peripheral European economies, viz., Greece, Ireland, Italy, Portugal, and Spain (GIIPS) are known to be the most vulnerable markets when it comes to contagious market shocks. Theoretical and practical evidence suggests that highly integrated markets leave behind negligible diversification prospects in terms of risk and portfolio management. As the focus of the extant literature has been on the negligence of GIIPS stock markets, a study that investigates the drivers of the comovements of GIIPS stocks is essential to offer insights into asset allocation and portfolio management strategies. In this study, the role of investor expectations and fear in the interdependencies and similarities of GIIPS stock markets' returns are analyzedin a multiscale paradigm using a set of wavelet techniques: bi-, partial, and multiple wavelets.
The study adds to the emerging strands of literature that investigate the impact of uncertainties in the US on the vibrant market and/or regional blocs. Specifically, we contribute to the recent strands of literature on GIIPS that assess the linkages between the markets and external macroeconomic factors (e.g., Riaz et al., 2020) and those that examine the influence of external variables on regional markets (e.g., Owusu Junior et al., 2021b; Asafo-Adjei et al., 2022). Our documented comovement dynamics of GIIPS stock markets and investor sentiments (the US VIX) provide insights across different timescales that are of practical significance to short-, medium-, and long-term investors.
In the time-frequency domain, we find that pairs of GIIPS markets are highly interrelated with similar patterns. The similarities in the comovement of GIIPS stock markets suggest that investors could simply select any of the GIIPS stocks and allocate investable funds, however, keeping multiple GIIPS assets leaves no diversification prospects. By corroborating previous evidence (e.g., Owusu Junior et al., 2021a; Shahzad et al., 2022), the negative or VIX-driven comovement of GIIPS markets and investor expectation and fear imply that the US VIX could serve as a hedge for GIIPS stocks across divergent timescales. This answers the question of "what other safe asset could be employed for equity-dominated portfolios when the bond markets fail as a result of sovereign debt crises?" The Spanish stock index, across all frequencies at normal trading periods, has the potential to lead or lag the remaining GIIPS markets while in turbulent trading periods, the potential lead/lag role is distributed among Spain, Italy, and Ireland across the short-, medium-, and long-term horizons. More importantly, in systemic risk periods like the COVID-19 era, the Irish stock market leads the remaining GIIPS markets, making it the first to recover from long-term shocks.
Our findings have important implications for economic or market regulators, financial market players, and economists. The high integration between GIIPS communicates the need for strategic asset allocation between GIIPS and other markets. Although individual GIIPS markets' shocks could be hedged against using the US VIX, investors should be wary of the idiosyncratic shocks that are propagated by individual GIIPS markets since they could overturn diversification benefits. We recommend that owing to their similarities, the implementation of economic recovery policies need not be left with specific markets. For instance, among GIIPS, Ireland is the only country that has initiated economic recovery policies. We advocate that without a synchronized initiation of recovery policies, the effectiveness of such policies may take longer than expected and stock market performance would continue worsening, driving away substantial capital flows.
Future studies could consider the makeup of the VDAX and assess whether assets from the EU countries that are closely linked to the VDAX are indeed influenced by such an uncertainty measure.
Data Availability
The data on stock indices that support the findings of this study are licensed by EquityRT while the US VIX is publicly available at the database of the Chicago Board Options Exchange.
Acknowledgments
We are very grateful for the useful comments of four anonymous referees. We are responsible for any surviving errors.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:










