1. Introduction
Embedded crack located near free surface of a component interacts with the component free surface. The interaction is significantly affected by the crack shape and its location. Namely, when the distance between the embedded crack and thefree surface is short, stress at the crack tip ligament is higher than that at the other area of the cracked section. Besides, when the crack aspect ratio a/l is small, the stress intensity factor at the tip of the embedded crack at the free surface side increases, where a is the crack depth and l is the crack length. It can be easily expected that the fatigue crack growth for the embedded crack is fast, when the embedded crack is located near the free surface. Thisphenomenon of the fatigue crack growth rate increase is well known as an interaction of the free surface on the stress intensity factor.
To avoid catastrophic failures caused by fast fatigue crack growth, fitness-for-service (FFS) codes provide crack-to-surface proximity rules [1]. Theproximity rules are used to determine whether the cracks should be treated as embedded cracks as-is, or transformed tosurface cracks. There are about 13 FFS codes in the world. Although the concepts of the proximity rules are the same, the specific criteria and the rules to transform embedded cracks into surface cracks differ amongst FFS codes. This re-characterization concept is essential and important for embedded cracks in the crackevaluation procedures.
The objective of the paper is to introduce the interaction between the embedded cracks and the free surface of the component, and to analyse its impact on the remaining fatigue lives of embedded cracks using proximity rules provided by FFS codes. It is shown that the fatigue remaining lives are significantly different among the FFS codes.
2. Interaction of Stress Intensity Factor of Embedded Crack Due Free Surface
Stress intensity factor is a fracture mechanics parameter to predict stress state near a tip of a crack caused by a remote loading. The equation of the stress intensity factor is basically described by crack size, applied stress and component geometry. The value of the stress intensity factor is affected by not only an adjacent crack but also the component free surface. The increase of the stress intensity factor by an adjacent crack and or the component free surface is called as interaction of stress intensity factor.
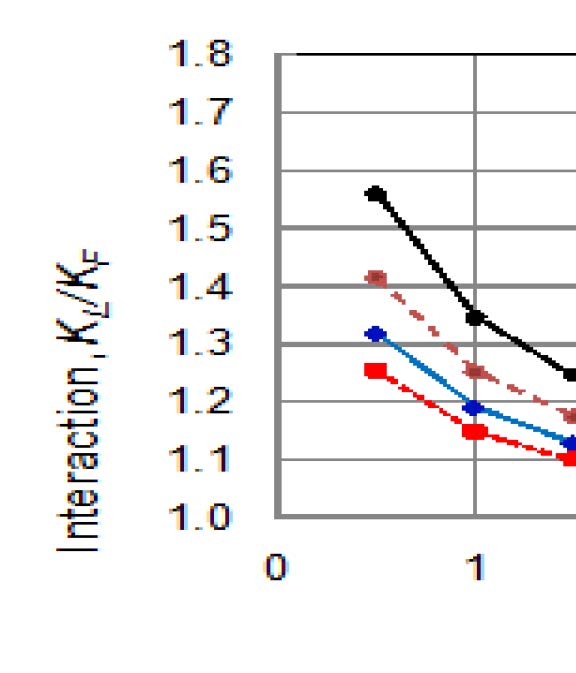
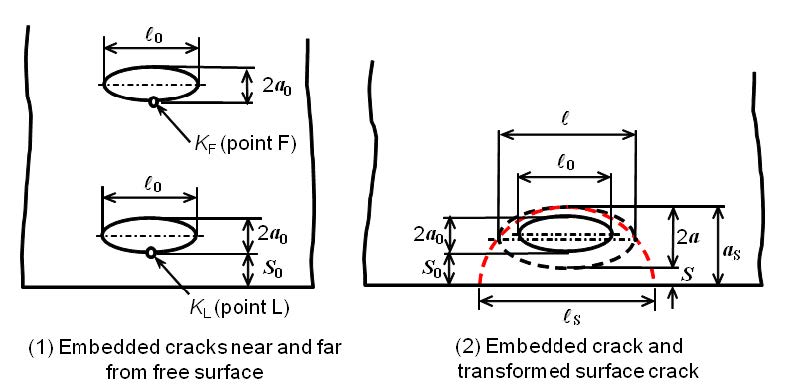
Figure 1(1)illustrates embedded cracks near the free surface and far from the free surface in a semi-finite body, where 2a0 is the initial depth, l0 is the initial length for the embedded crack and S0 is the initial ligament distance between the free surface and the embedded crack. Stress intensity factors at the points F (KF) and point L (KL) were obtained by the XFEM (extended finite element method) analysis for the same size embedded cracks [2]. The stress intensity factor KF is not affected by the free surface because of long distance from the free surface. On the other hand, the stress intensity factor KL is affected by the free surface. The ratio of KL/KF represents the interaction caused by the component free surface.
Interaction of stress intensity factor for an embedded crack is shown in Figure 2, as a parameter of crackaspect ratio a0/l0. It can be seen that, from Figure 2, the stress intensity factor interaction increases with a decrease in the distance S0 and in the aspect ratio a0/l0 [2]. It is suggested, for a conservative for structural integrity estimation a cracked component, that the embedded crack shall be replaced to a surface crack when S and a/l are small.
The re-characterization criteria of the proximity rules from embedded to surface crack are different amongst FFS codes, as mentioned before. In order to confirm the adequacy of the limit value for the crack-to-surface proximity factor Y, where Y is given as Y = S/a, fatigue crack growth experiments were conducted for carbon steel plates containingembedded cracks at ambient temperature [3]. Crack growth behaviour from embedded to surface crack was observed by using beach marks on the crackedfaces in the experiments. In addition, equivalent fatigue crack growth rates for embedded cracks with different aspect ratios were calculated by the XFEM analysis. From the results of the experiments and calculations, the proximity factor Y was found not to be constant. The proximity criterion proposed by experimentsand calculations is Y = 1.0 - 1.4(a/l) for 0 < a/l ≤ 0.5 and Y = 0.3 for 0.5 < a/l [3]. This means that the interaction for embedded crack with small a/l at long distance is equivalent to that for embedded crack with large a/l at short distance. That is, the embedded crack with small a/l shall be transformed to a surface flaw at far distance from the component free surface.
3. Proximity Rule Provided by FFS Codes
Asingle embedded crack is assessed to be treated as an embedded crack, or transformed into a surface crack, in compliance with the proximity criterion, as described earlier. The transformation of an embedded crack to a surface crack is illustrated in Figure 1(2), where as is the transformed surface crack depth, l/s is the length of the transformed surface crack, and S is the ligament distance from the embedded crack to the component free surface. This transformation procedure is used for fatigue crack growth calculations and for the fracture assessment.
The reason for the transformation from the embedded to the surface crack is the high stress experienced by the narrow ligament due to the presence of the crack, which can lead to ligament fracture. In fact, the stress intensity factor at the ligament side of embedded crack is always high, as shown in Figure 2. Initiation of fracture of the component is thus expected to occur at the ligament of the embedded crack. Therefore, the embedded crack located near the free surface should be replaced by a surface crack from the safety point of view for the assessment purpose.
The ASME Code Section XI [4] defines the proximity criterion as follows: if S/a < 0.4, an embedded crack is classified as a surface crack, of which length is ls = l for as/ls ≤ 0.5, and ls = 2(2a + S) for as/ls > 0.5. The JSME Code S NA1 [5] has the same criterion with the ASME Code Section XI.
In the American Petroleum Institute (API) 579 [6], an embedded crack is transformed to a surface crack based on the ratio of S/t < 0.2, irrespective of the crack depth a, where t is the wall thickness. The length of thetransformedsurface crack is ls = 2S + l.
The French Code RSE-M [7] used for in-service inspection of nuclear power plants gives S/a < 1.0. The length of the transformed surface crack depends on the surface crack aspect ratio a/l. If a/l < 0.5, the length is given by ls = maximum of [l, 2(2a + S)]. If a/l < ; 0.5, then ls = 2(2a + S), which is a semi-circular crack.
The Japanese Welding Engineering Society Code WES 2805 [8] isapplicable to welded joints of steel components. An embedded crack is transformed to a surface crack, if S/a < 0.25. The length of the surface crack is ls = l.
The AME [9] Czech assessment Code provides as follows; An embedded crack is transformed to a surface crack, if S/a < 0.11. The transformed length of the surface crack is the same as the original crack length, that is ls = l.
Although the concepts of the proximity rules to transform an embedded into a surface crack are the same amongst FFS codes, the specific criteria are different. Therefore, the estimated final results of the transformed surface crackgrowth will be different, even when the initial embedded cracksizes and locations are the same. It is expected that the predicted remaining lives of the components containing same size embedded cracks might vary considerably amongst FFS codes.
4. Calculation Conditions of Fatigue Crack Growth
In order to obtain the predicted remaining lives for pipes with embedded and transformed surface cracks, fatigue crack growth calculations were conducted based on FFS codes. The pipe size employed consists of 12-in. (318.5 mm) Schedule 80 diameter with various circumferential embedded cracks. The wall thickness of the 12-in. diameter pipe is 17.4 mm. The circumferential embedded cracks are located near the inner surface of the pipes.
The applied cyclic loading is a membrane stress, where the maximum stress is σmax = 123 MPa, corresponding to the allowable design stress for stainless steel [10], and minimum stress is σmin = 0 MPa. The stress ratio of R is R = σmin/σmax = 0. Table 1 shows the embedded crack sizes considered for the calculations. These crack sizes are slightly larger than the allowable crack sizes for pipes provided by the Acceptance Standard in the ASME Code Section XI [4].
Table 1. Analytical conditionsof embedded cracks.
| t, mm | a0, mm | l0, mm | a0/l0 | S0, mm |
| 17.4 | 1.74 | 58.0 | 0.03 | 2.0 |
| 4.0 |
| 17.4 | 0.10 | 2.0 |
| 4.0 |
| 2.61 | 10.44 | 0.25 | 2.0 |
| 4.0 |
| 5.22 | 0.50 | 2.0 |
| 4.0 |
Fatigue crack growth rate used for calculations is provided by the ASME Code Section XI, Appendix C [4]. The fatigue crack growth rate for austenitic stainless steel in air environment is given by;
where da/dN is the fatigue crack growth rates in mm/cycle, ΔKI is the stress intensity factor range in the unit of MPa·√m, C is a scaling parameter to account for temperature and S is a scaling parameter to account for R ratio. The C and S parameters are given by,
|
C=10[−8.714+1.34×10−3T−3.34×10−6T2+5.95×10−9T3]
|
(2)
|
|
S=1.0,when R≤0S=1.0+1.8R,when 0<R≤0.79S=−43.35+57.97R,when 0.79<R<1.0}
|
(3)
|
where T is the metal temperature (for T ≤ 430 °C) and used herein as room temperature. As the R ratio is 0, the scaling parameter is S = 1.0 in the calculations.
The stress intensity factors for embedded cracks were calculated using the equations by Miyazaki, et al. [11]. During the calculation, the embedded crack is assumed to be an elliptical shape. When the aspect ratio a/l of the embedded crack flaw is beyond 0.5, stress intensity factor coefficient was obtained by extrapolation from a/l = 0.4 and 0.5.
After the transformation to the surface crack, the stress intensity factor for the surface crack was calculated by using the ASME Code Section XI [4]. The stress intensity factors for surface cracks in pipes are almost the same as that in plates [12]. Therefore, the stress intensity factors for flat plate solutions provided by the ASME Code Section XI were used in lieu of the stress intensity factors for pipes. In accordance with the ASME Code, a surface crack with the aspect ratio of a/l > 0.5 is replaced with a semi-circular crack of a/l = 0.5. Therefore, stress intensity factor for a/l = 0.5 is used for the surface crack, when a/l > 0.5.
During the fatigue crack growth calculations, the embedded crack approaches to the free surface, and the embedded crack is transformed to surface crack, when the distance S is satisfied with the criterion provided by each FFS code. Crack depths are not allowed exceeding 75% of the nominal wall thickness, in compliance with the ASME CodeSection XI. Therefore, fatigue crack growth calculations were performed until 75% of nominal wall thickness. Number of cycles at the crack depth of 75% of nominal wall thickness is defined as fatigue remaining life. During the fatigue crack growth calculations, the cracks might reach the critical depth leading to fracturebefore reaching 75% of the nominal wall thickness. For assessing the remaining fatigue lives, the critical depths with respect to fracture were not considered herein.
5. Fatigue Crack Growth From Embedded to Surface Crack
Fatigue crack growths in the thickness direction were obtained by fatigue crack growth analysisusing Eqs. (1) to (3). During the growth of the embedded cracks, the embedded cracks were transformed to surface cracks when the proximity criteria provided by FFS codes were met. When the crack depth grows to 13.05 mm in the thickness direction, which corresponds to the 75% of the wall thickness t, the calculations were terminated. Fatigue crack growths are obtained using the proximity rule of the API, RSE-M, Y(a/l), ASME, WES and AME, where Y(a/l) denotes the proximity rule of Y = 1.0 − 1.4(a/l) for 0 < a/l ≤ 0.5 and Y = 0.3 for 0.5 < a/l, as mentioned before.
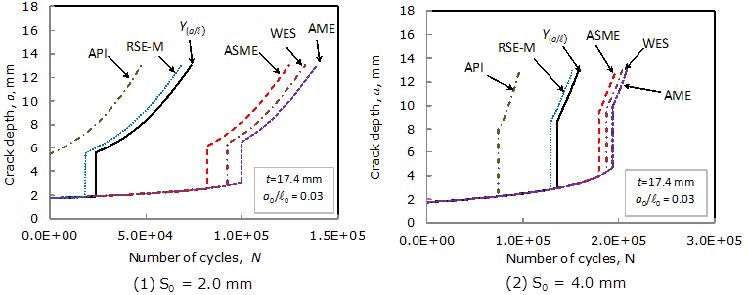
Table 2 tabulates the number of cycles at transformation from embedded crack to surface crack for each FFS code. In case of the API calculations for S0 = 2.0 mm, the embedded cracks are classified as surface cracks at the starts of the calculations because 2.0 mm is less than 20% of the wall thickness. In addition, in case of the RSE-M calculations for S0 = 2.0 mm with a0/l0 = 0.25 and 0.50, the embedded cracks are treated as surface cracks. This is because the embedded crack depths of a0 = 2.61 mm are beyond the distance of S0 = 2.0 mm. The numbers of cycles at the transformation are considerably different amongst FFS codes, as shown in Table 2.
Table 2. Number of cycles at transformation by FFS codes.
| a0/l0 | S0, mm | API | RSE-M | Y(a/l) | ASME | WES | AME |
| 0.03 | 2 | - | 18,400 | 23,900 | 82,100 | 92,500 | 99,900 |
| 4 | 74,600 | 129,000 | 135,700 | 179,500 | 187,800 | 193,000 |
| 0.10 | 2 | - | 24,600 | 51,500 | 120,800 | 140,700 | 157,300 |
| 4 | 96,700 | 174,300 | 213,000 | 264,200 | 285,200 | 303,100 |
| 0.25 | 2 | - | - | 87,600 | 87,600 | 122,600 | 154,300 |
| 4 | 84,200 | 110,000 | 237,200 | 259,500 | 297,600 | 332,500 |
| 0.50 | 2 | - | - | 265,500 | 212,400 | 291,100 | 358,400 |
| 4 | 190,900 | 244,000 | 561,000 | 519,600 | 580,800 | 632,900 |
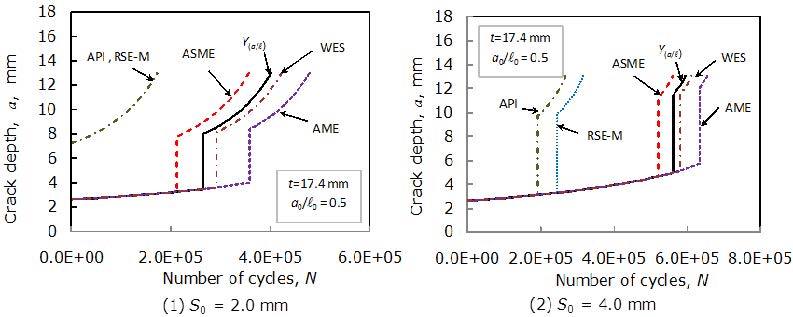
Fatigue crack growth depths a vs number of cycles N areshown in Figures 3 to 6, where the initial embedded cracks are located at S0 = 2.0 and 4.0 mm. Figure 3 shows the fatigue crack depths for the initial flaw depth with 2a0 = 3.48 mm, l0 = 58.0 mm and a0/l0 = 0.03. Remaining fatigue lives at a = 0.75t are significantly different among FFS codes. The API and RSE-M give short remaining fatigue lives. The remaining fatigue life given by the Y(a/l) is close to the curve of the RSE-M. The lives estimated by the ASME, WES and AME are longer than that by the Y(a/l). When the distance S0 becomes large, all remaining lives become longer.
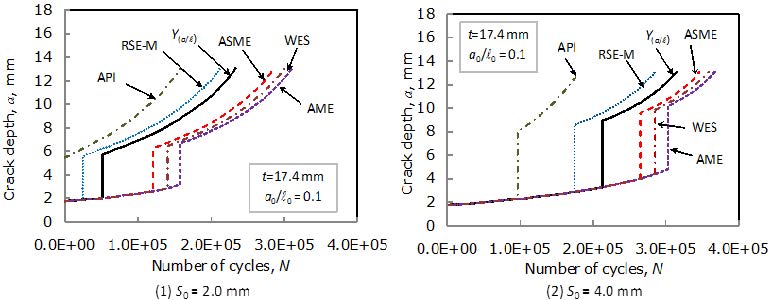
Figure 4 shows the relationship between fatigue crack depths and number of cycles forpipes where the initial crack is 2a0 = 3.48 mm, l0 = 17.4 mm and a0/l0 = 0.10. The API gives short remaining life and the AME gives long remaining life. The tendency of the remaining lives obtained for each FFS code is similar to Figure 3. However, the remaining life expressed by the Y(a/l)approaches those calculated by the ASME, WES and AME, compared with the remaining lives in Figure 3. When the aspect ratio and ligament distance increasefrom a0/l0 = 0.03 to 0.10 and S0 = 2.0 to 4.0 mm, fatigue remaining lifebecomes longer. This means that the interaction with the free surface decreases when the aspect ratio and the ligament distance increase.
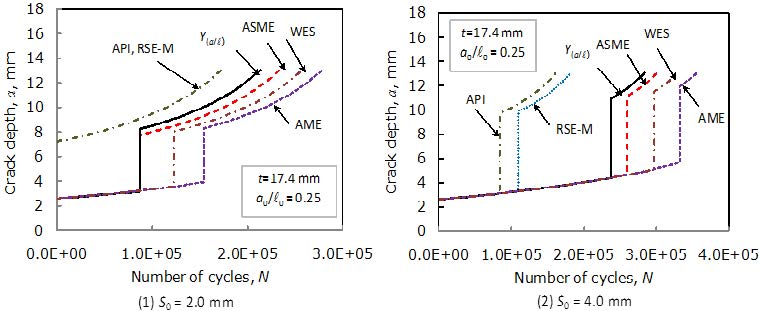
Fatigue crack growth depths with 2a0 = 5.22 mm, l0 = 10.44 mm and a0/l0 = 0.25 are shown in Figure 5. Fatigue crack growth curve for the RSE-M is the same with as for the API, when S0 = 2.0 mm, as shown in Figure 5(1). This is because the initial embedded crack depth is treated as a surface crack at the start of calculations for both the API and the RSE-M codes. It is shown that fatigue crack growth curve given by the Y(a/l) is close to that given by the ASME, as shown in Figure 5(2).
Figure 6 shows the fatigue crack growth curves for circular cracks, where 2a0 = 5.22 mm, l0 = 5.22 mm. The remaining fatigue lives given by the API and the RSE-M are very small compared with those given by the Y(a/l) and the other FFS codes. The fatigue life given by the ASME is slightly smaller than that by the Y(a/l). The remaining life given by the AME is always longest amongst the FFS codes.
6. Discussion of Remaining Lives Determined by FFS Codes
As the proximity criteria provided by FFS codes are different, remaining fatigue lives are significantly different, although the initial embedded cracks are the same size and same locations. It is found that the remaining fatigue lives for embedded cracks strongly depend on the proximity criteria, together with crack aspect ratios and locationsfrom the component free surfaces. Table 3 shows the number of cycles at remaining fatigue lives by FFS codes.
Table 3. Number of cycles at remaining fatigue lives by FFS codes.
| a0/l0 | S0, mm | API | RSE-M | Y(a/l) | ASME | WES | AME |
| 0.03 | 2 | 47,600 | 68,500 | 73,500 | 124,600 | 133,000 | 138,900 |
| 4 | 97,100 | 152,100 | 158,200 | 197,200 | 204,100 | 209,100 |
| 0.10 | 2 | 158,200 | 212,100 | 233,800 | 286,600 | 300,400 | 311,100 |
| 4 | 180,500 | 285,000 | 314,600 | 346,600 | 358,300 | 367,900 |
| 0.25 | 2 | 172,700 | 172,700 | 213,700 | 233,800 | 257,500 | 278,400 |
| 4 | 161,600 | 182,600 | 284,100 | 301,400 | 330,500 | 356,400 |
| 0.50 | 2 | 172,700 | 172,700 | 401,700 | 356,800 | 478,200 | 423,000 |
| 4 | 268,000 | 316,300 | 595,200 | 560,200 | 611,800 | 654,300 |
The proximity criterion for the API based on wall thickness of S < 0.2t does not consider crack interaction and it gives unduly conservative prediction. In accordance with the API, components containing an embedded crack near free surface might be requested unnecessary repair or replacement.
The RSE-M gives relatively short remaining lives, where the proximity criterion is given as S < 1.0a. When the initial aspect ratio of the embedded crack is small such as a/l = 0.03 or 0.1, the remaining fatigue life is close to the fatigue life calculated by the proximity criterion of the Y(a/l). However, when the aspect ratio is large, the remaining life of the RSE-M is considerably shorter than that of the Y(a/l). The criterion of S < 1.0a is suitable for small aspect ratio crack, and, alternatively, it gives overly conservative life for large aspect ratio crack.
The proximity criterion of the ASME is S < 0.4a. In case of small crack aspect ratio, the ASME gives longer remaining lives, compared with those by the Y(a/l). On the other hand, when the aspect ratio is large circular crack, the remaining life is shorter than that by the Y(a/l). It can be said that the ASME gives non-conservative lives for small aspect ratio crack and conservative lives for large aspect ratio crack.
The proximity criteria provided by the WES and the AME are S < 0.25a and S < 0.11a, respectively. These criteria show that the embedded cracks are transformed to surface cracks when the embedded cracks are very close to the component free surfaces. The interaction between the embedded crack and the free surface is presumed to be large just before the transformation. Number of cycles under the condition of the embedded crack is long, and the number of cycles under the condition of the transformed surface crack is short. The remaining fatigue lives estimated by the WES and the AME are long and they give non-conservative evaluations.
7. Conclusion
The interaction between embedded cracks and the component free surfaces affects the remaining fatigue lives of the components. The embedded cracks located near the free surfaces are transformed into surface cracks in accordance with proximity criteria. Remaining fatigue lives for pipes withembedded cracks were calculated using crack-to-surface proximity criteria provided by FFS codes. As a result of the calculations, it can be concluded as follows:
The remaining fatigue lives are significantly different amongst FFS codes, although the initial embedded cracks are the same size and same locations. The lives depending on the proximity criteria are also governed by crack aspect ratios and locations from component free surfaces. The API and the RSM-E which give short remaining lives are overly conservative evaluations. On the contrary, the WES and the AME which give long remaining lives are non-conservative evaluations. The ASME gives non-conservative evaluation for embedded crack with small aspect ratio and it gives conservative evaluation for the crack with large aspect ratio.
Conflict of Interest
The authors declare that there are no conflicts of interest in this paper.









 DownLoad:
DownLoad: