1. Introduction

The ability to determine the fatigue life for a damaged structure has become increasingly important with the advent of the damage tolerance criteria mandated by Federal Aviation Administration (FAA) regulations for ageing transport aircraft. Consequently, the lap or butt joint designs have been compared on the basis of their fatigue behaviour performances.

Numerical simulations are useful to identify the most fatigue critical locations where to check the effects of a possible crack, growing under a given load spectrum.

During the past, extensive research has been developed in the area of the riveted joint performances ^{[1,2,3,4,5,6]}, analysed in relation to performances of different joint techniques, e.g., Friction Stir Welded (FSW) joints ^[7] or bonded joints ^[8]. Most of the numerical analyses have been performed by using the Finite Element Method (FEM), but some works have also been done by using the Dual Boundary Element Method (DBEM) ^[9,10] or using a combination of both techniques ^[11].

In this work a Multi Site Damage (MSD) crack growth simulation is presented, carried out by means of Dual Boundary Element Method (DBEM), as implemented in the commercial code BEASY ^[12].

The analysis refers to a lap-joint, affected by the simultaneous initiation and propagation of different cracks from the most loaded holes. The numerical model is bidimensional, even if the lack of a three dimensional modelling introduces an element of approximation of the real phenomena because of the secondary bending effects (Figure 1), responsible for a non-straight crack propagating front. Such phenomena can only be modelled in a three-dimensional approach, but such constraint can be relaxed when the cracks analysed are sufficiently long in relation to the joined plates’ thicknesses ^[13]. Moreover, residual stress effects on crack propagation will be neglected because the cracked holes are not cold worked ^[14].

The reproduced MSD scenario was obtained experimentally in ^[15] and analysed also in ^[16], where a FEM numerical simulation of multiple crack propagation was shown.

---

2. Problem Description

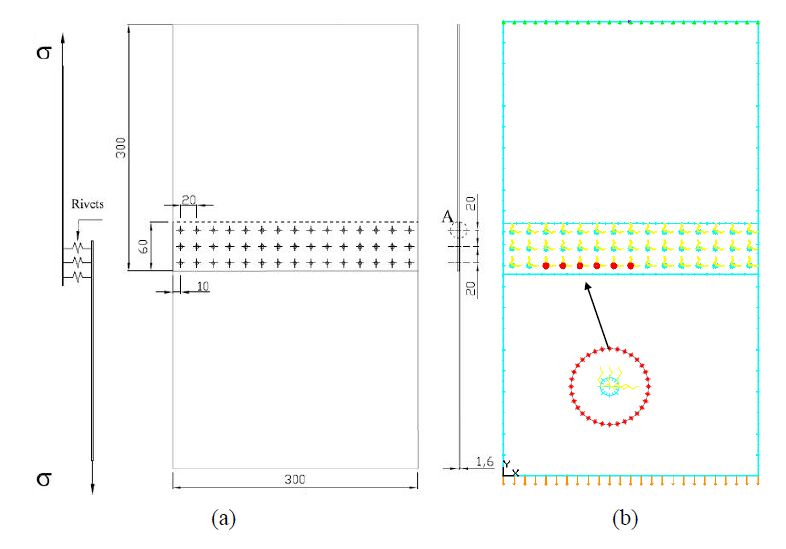
The lap joint considered has three rivet rows and undergoes a remote traction fatigue load (Figure 2a), with σ_max = 110 MPa and R = σ_min/σ_max = 0.1.

The material behaviour is considered as linear elastic. The adopted mesh (Figure 2b) is based of nearly one thousand linear elements; such number increases along the cracks propagation by addition of new elements to model the growing cracks.

When the initial crack length is much lower than hole radius, nonlinear contact conditions between rivet and corresponding hole are modelled by “GAP” elements (Figure 2) ^[17,18].

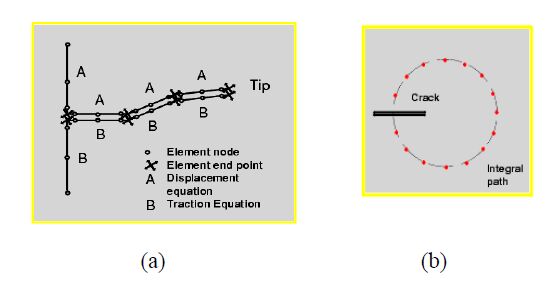
The crack faces are discretised with “discontinuous” ^[12] elements and the Stress Intensity Factors (SIFs) are calculated by the J-integral approach ^[19,20] (Figure 3). In particular BEASY code ^[12] splits the J integral is in two parts: the symmetric (J_I) and antisymmetric (J_II) parts which, for plane stress conditions (like in this case), respectively relates to mode I and mode II SIFs as in the following:

${{\text{K}}_I} = \sqrt {E{J_I}} \qquad {\text{and}} \qquad {{\text{K}}_{II}} = \sqrt {E{J_{II}}}$

(1)

Crack growth rates are calculated by the well-known Paris’ law:

$da/dN = C \cdot \Delta K_{eff}^n$

(2)

with calibration parameters n = 3.333 and C = 0.747E−12 (the latter valid for da/dN units in mm/cycles and ΔK_eff units in MPa·mm^0.5) ^[15,16]. The formula used by default in BEASY code to calculate ΔK_eff is the following (Yaoming Mi approach):

$\Delta {{\text{K}}_{eff}} = \sqrt {\Delta K_I^2 + 2\Delta K_{II}^2}$

(3)

Each panel has a thickness equal to 1.6 mm and is made of aluminium alloy 2024-T351 with Young’s modulus E = 73.1 GPa, Poisson’s coefficient ν = 0.33 and yield stress σ_y = 324 MPa.

Rivets are made of Al 2017-T31 with Young’s modulus E = 72.4 GPa and Poisson’s coefficient ν = 0.33; rivet diameter is equal to 4.8 mm.

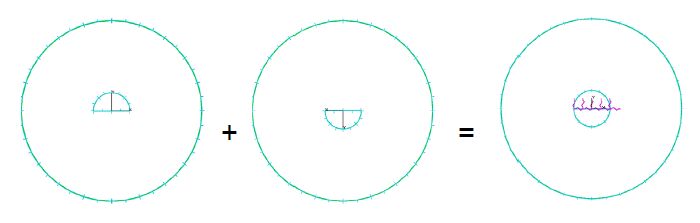
The multi-layer approach adopted (see ^[17] for more details) allows to model the joined plates with their effective membrane stiffness (each plate is represented by a different layer with corresponding thickness and material properties) and the rivets with their effective shear stiffness. The rivets are used to connect the interacting layers and are modelled as two circles (Figure 4), representative of the two halves in which the rivet is split; such two halves are connected by an internal spring whose stiffness, equal to K = 33052 N/mm, is calibrated in order to model the shear stiffness of the rivet ^[21]. More in details, each rivet half interacts with one plate and the two rivet parts are connected by creating fictitious boundaries in the centre of circle where to apply the spring (Figure 4).

The rivets adjacent to plate border (those indicated with capital letters in Figure 5) are cold worked in order to avoid premature crack initiation.

The crack growth direction is evaluated based on the criteria of maximum principal stresses at crack tip ^[22].

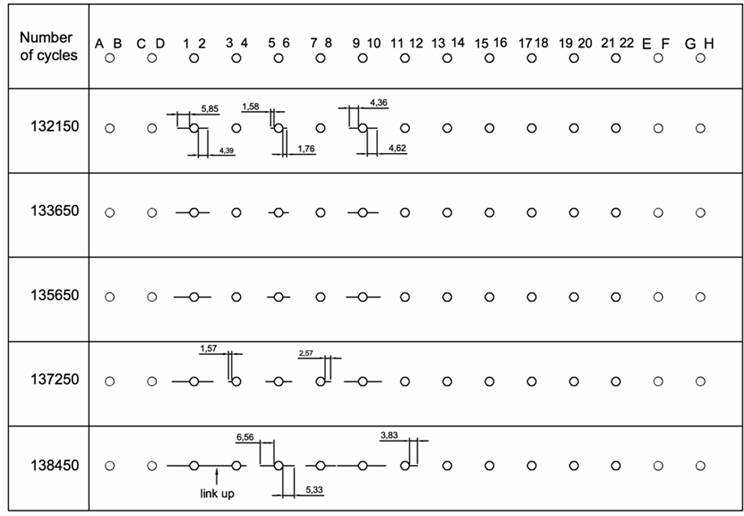
The crack initiation in the numerical model follows the sequence of initiations recorded during the experimental test ^[15,16]. In Figure 5, the experimental MSD crack configurations are shown at different stages of crack propagation, with potential crack initiation sites numbered from N.1 to N.22 (no initiation is expected at cold worked holes).

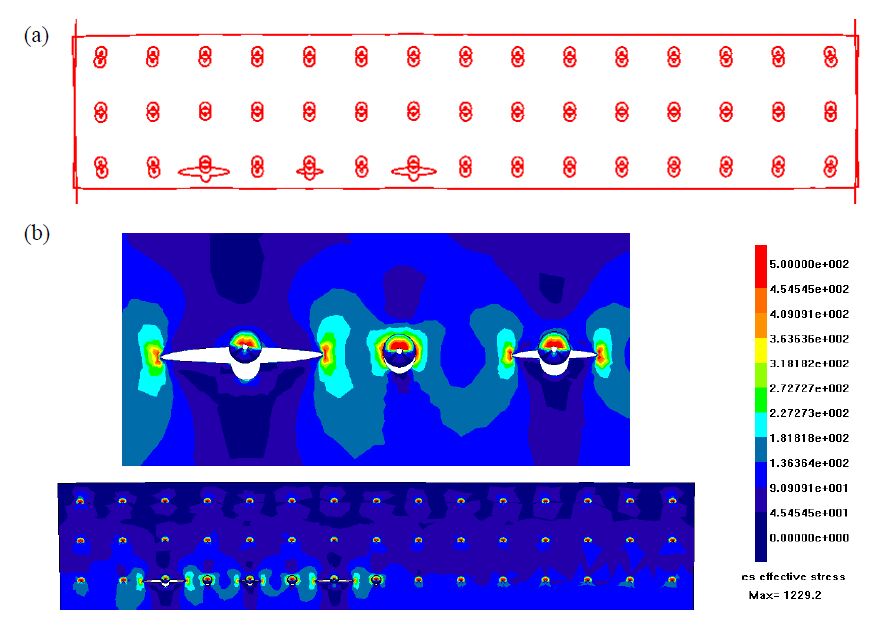
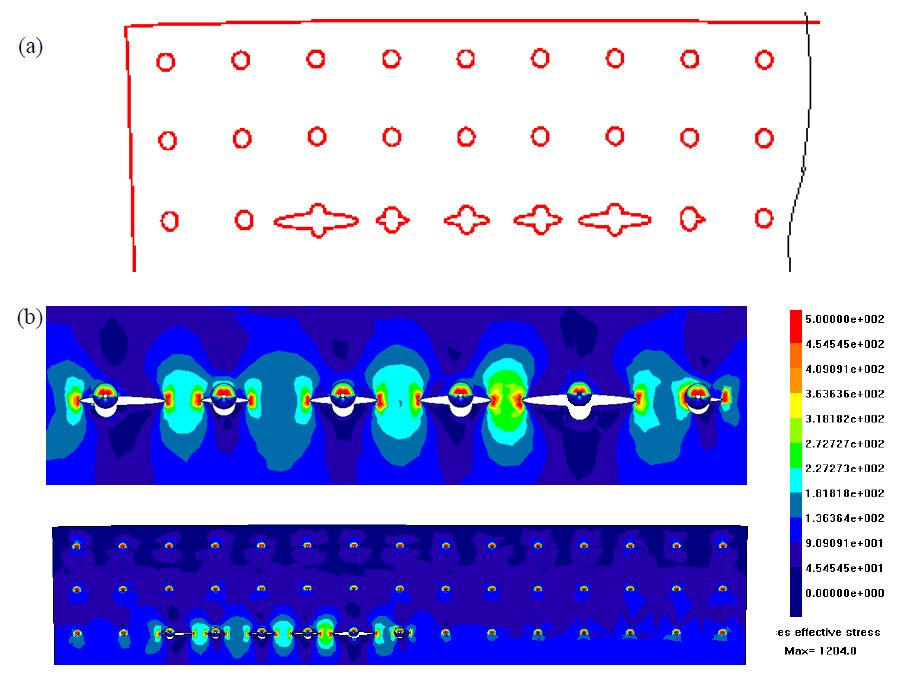
The numerical initial crack configuration is that corresponding to the experimental scenario obtained after 132450 fatigue cycles: in Figure 6a and 6b the deformed plot of the joint and the corresponding stress scenario are respectively shown; the latter, referred to the cracked plate (the other one remains intact), allows to point out the most critical areas. Same outcomes are provided in Figure 7a and 7b but with reference to a higher number of cycles.

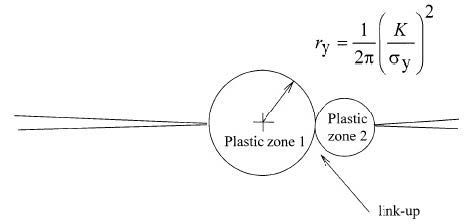
Applying the Swift’s criterion (Figure 8) to the configuration of Figure 7b, it is possible to see how the plastic zones related to approaching crack tips N.2-3 and N.8-9 are touching and consequently an hypothesis of crack coalescence can be formulated. Such numerical outcome turns out to be consistent with experimental data (Figure 5).

---

3. Results

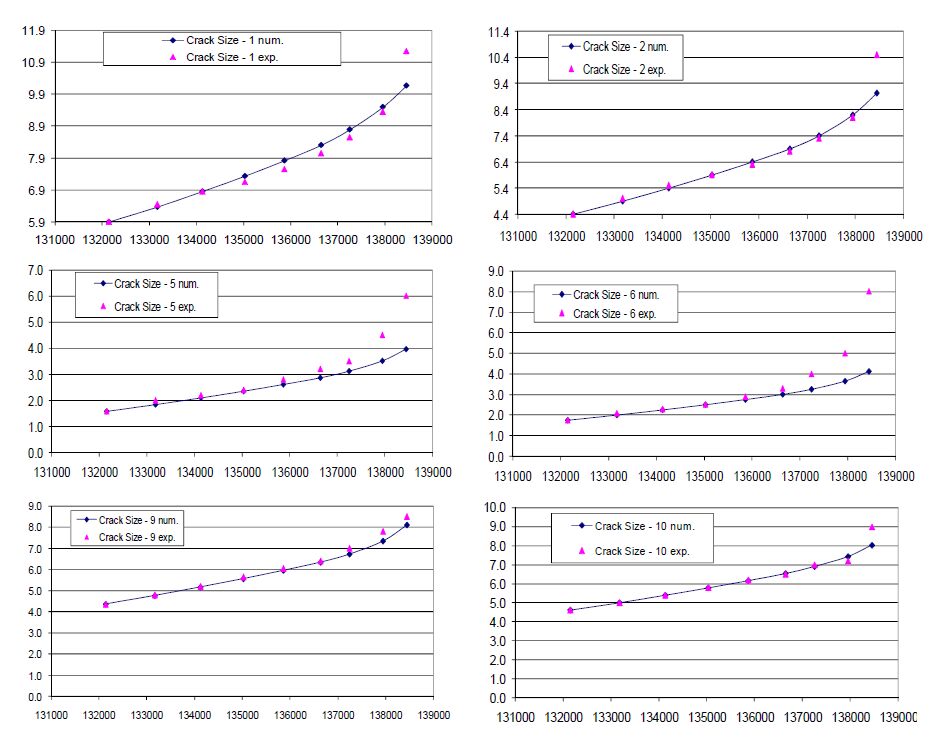
In Figure 9, experimental and numerical results in terms of crack advances vs cycles are reported: just in the final stage of crack propagation there appears non negligible discrepancies between them as a consequence of the simplified crack growth law (Eq. 2) adopted. As a matter of fact, the Paris’ law cannot allow for the sudden crack growth acceleration occurring when K_effmax approaches the material fracture toughness K_c. Another secondary reason for the aforementioned discrepancies can be retrieved in the violation of LEFM hypothesis due to enhanced yielding arising in the final stage of crack propagation (with related crack coalescences).

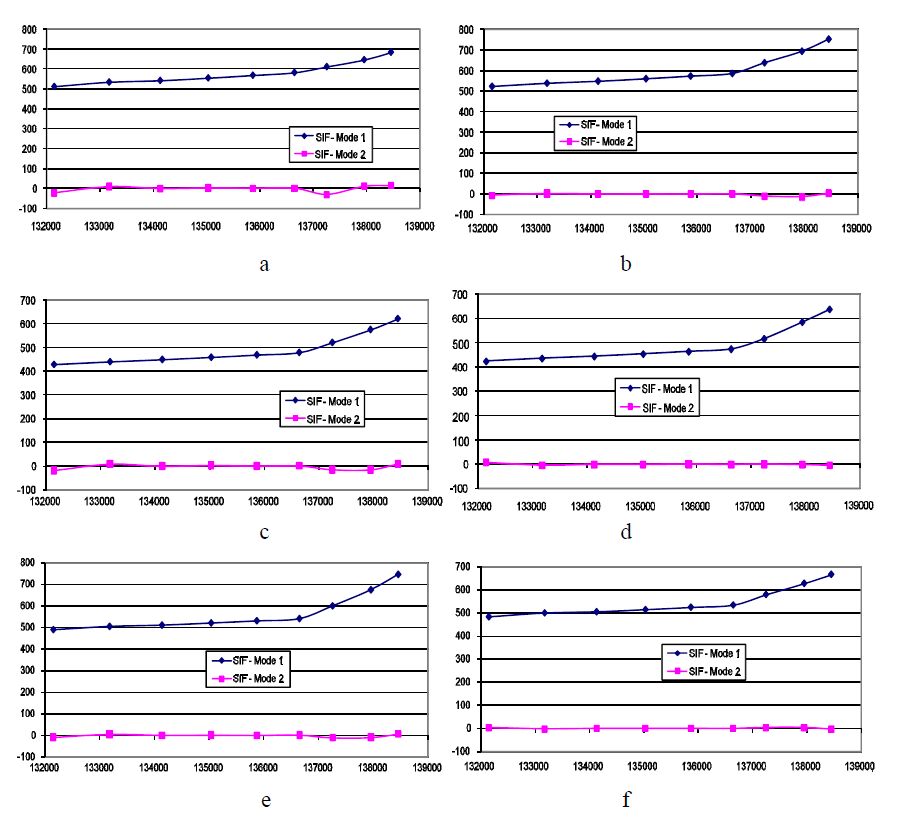
In Figure 10, SIFs are shown with reference to the considered growing cracks: the crack propagation turn out to be under pure mode I and that is why just the K_I values are reported.

A satisfactory accuracy of DBEM results can be stated by comparison with FEM results available from literature ^[15,16].

---

4. Conclusion

The illustrated DBEM bidimensional approach exhibits very short run times to run the whole MSD crack propagation and an easy preprocessing phase is enabled: an automatic remeshing is possible as the crack grows and the manual intervention is just necessary in order to initiate new cracks. Even in the proposed simplified bidimensional approach, each lap joint individual layer is explicitly modelled and connected to each other by rivets. When necessary, gap elements have been used at the pin-hole interface.

A simplified approach like that presented here, with related very short run times, becomes mandatory in case of a probabilistic approach to crack propagation simulation, where hundred thousands of such simulations are to be performed (e.g., when resorting to Monte Carlo method…).

The numerical-experimental correlations obtained by the proposed DBEM procedure are satisfactory as proved by comparison with available numerical (FEM) and experimental results.

---

Conflict of Interest

All authors declare no conflict of interest.

---