Dynamic correlation among title transfer facility natural gas, Brent oil and electricity EPEX spot markets: Spillover effects of economic shocks on returns and volatility

1.   Introduction

In recent years, energy markets have experienced important upheaval, exerting a substantial impact on the European economy and contributing to increased living costs and inflation ^[1]. These markets are marked by intricate geopolitical factors, amplifying the instability in various sectors and industries due to pronounced price volatility ^[2,3,4,5]. Notably, oil and natural gas (NG) stand out as the most pivotal commodities among the energy sources, with biofuels also meriting attention ^[6,7]. Despite their importance, existing literature has predominantly focused on the adverse effects of rising oil and natural gas prices on economic growth ^[8]. For oil, two primary reasons are typically cited to rationalize these effects: their critical roles as inputs in the production process and the perception of crude oil as a lucrative investment asset ^[9,10]. Indeed, Brent oil continues to hold a crucial position in the transportation industry and as a raw material for the chemical industry. Consequently, forecasting oil prices remains a relevant action to ensure energy supply security and to inform policymakers ^[11].

However, the influence of NG has also been expanding in global energy markets ^[12]. This was particularly noticed with the war in Ukraine and the European Union (EU) sanctions against Russia, which led to a reduced importance of oil compared to NG and electricity in driving inflation and economic growth in Europe ^[13]. According to the International Energy Agency (IEA), NG consumption witnessed a robust 4.6% growth in 2018, contributing significantly to the overall increase in global energy demand ^[14]. NG also plays a pivotal role in achieving a fully decarbonized economy, aligning with the EU's decision to reduce greenhouse gas emissions by at least 55% by 2030 compared to 1990 levels ^[15]. It is worth highlighting that NG can be utilized across various sectors, including residential, commercial, industrial, power generation and transportation.

There is extensive literature addressing the impact of energy markets on economy and financial crises. Among them, ^[16] argues that oil price shocks can affect a country's performance due to their capacity to disrupt the purchase of goods and investment realization. Some studies ^[17,18,19] extend the vision on energy resources by investigating the relationship among various energy prices, power markets and clean energy stocks. Others, such as ^[20,21], analyze volatility spillovers between oil and stock markets in Europe, the United States of America (USA) and Gulf Cooperation Council (GCC) countries. ^[22,23] explore volatility spillovers between oil and natural gas and between energy markets and European energy stock prices. Additionally, ^[24] investigated the impact of European Union Allowance (EUA) price fluctuations on the stock performance of electricity firms, while ^[25] examined correlations between United States equity indices, European equity indices and the Chinese stock market.

The COVID-19 pandemic triggered a severe economic shock, resulting in an unprecedented adverse impact on world economies. Accordingly, ^[26] compares this recent crisis to the great economic recession of the subprime mortgage crisis (2007–2008). The global economy contracted by 3.3% in 2020 compared to the growth of 2.8% achieved in 2019. In particular, lockdowns had a profound impact on citizens' lifestyle and financial markets, as reported by ^{[27,28,29,30]}. The global economy also took a huge toll after the invasion of Ukraine by Russia. All countries were hit by higher commodity prices, especially in the energy and food industries. This geopolitical instability naturally hampered the recovery of the global economy in the post-pandemic phase ^[31]. For instance, the crude oil market suffered another shock in 2022, with prices skyrocketing from around 76 USD per barrel in January 2022 to over 110 USD in March 2022 ^[32]. Moreover, NG spot market prices exhibited exponential growth since the first half of 2021. For example, the IEA projected in its 2022 Q4 gas market report that global NG consumption is expected to increase at an annual average rate of 0.8% from 2022 to 2025 ^[33]. Several studies describe that these geopolitical factors had a significant impact on energy trade ^[34,35], energy prices ^[36,37] and counter-cyclically ^[38,39].

In recent decades, there has been an increased interest in modeling and forecasting the volatility of time series, as well as examining the relationships among them ^[40]. This heightened focus is a consequence of time series typically exhibiting time-varying conditional variance, commonly referred to as volatility, and correlations. Higher volatilities increase the risk of assets, while higher conditional correlations lead to an increased risk in portfolios. In this context, our interest lies not in examining the variance of such time series throughout the sample period but specifically in the varying or conditional variance. Another crucial phenomenon related to the relationships among time series is the spillover effect, which occurs when one event (e.g., oil price return) triggers another event (i.e., NG returns) in a similar manner ^[41]. These spillover effects and volatility have undergone detailed analysis. For instance, ^[42] investigated the volatility spillover between crude oil, natural gas and the S & P500 markets during the COVID-19 pandemic. Additionally, ^[43] implemented a time-varying Granger causality test to confirm the bilateral contagion effect between the World Trade Institute (WTI) and gold during this period. ^[44] adopted the Multifractal Detrended Fluctuation Analysis (MF-DFA) approach to analyze the asymmetric multifractality between Brent crude oil and gold prices, and ^[45,46] examined the dynamic spillover effects between bitcoin and crude oil during the pandemic crisis.

To thoroughly analyze these events, generalized autoregressive conditional heteroskedastic (GARCH) models have been widely employed in various types of portfolios for modeling time series volatility ^[47]. These models generalize ARCH models ^[48], as the conditional variance does not depend solely on previous squared error values but also on previous values of the same variance ^[47]. Therefore, as their main advantages, they allow for accommodating both effects: conditional standard deviations of the returns on stocks in the portfolio will co-evolve, and correlations between the returns will also vary ^[49]. There are several types of GARCH models, such as the exponentially weighted moving average (EWMA) model, the diagonal vector error correction (VEC) model, the dynamic conditional correlations (DCC) model, orthogonal GARCH or the dynamical orthogonal components model, whose usefulness has been confirmed in various studies involving energy markets. For example, ^[50] investigated the portfolio and hedging implications based on DCC and corrected DCC-GARCH models, reporting that oil-importing nations are significantly affected by lagged oil price shocks, although there is less evidence of interdependence between stock markets for both oil-importing and oil-exporting countries. Furthermore, ^[51] utilized DCC-GARCH models to assess the time-varying dynamics of value-at-risk (VaR) on daily stock returns of emerging markets. Results confirmed that this approach captures the volatility of stock returns better than traditional VaR models. Regarding the main limitations of GARCH models, ^[52] asserts that stock market returns are negatively correlated with changes in volatility returns, implying that volatility tends to rise in response to bad news and fall in response to good news. Another constraint is the non-negativity of parameters to ensure the positivity of the conditional variance ^[47]. Specifically, for multivariate GARCH models (MGARCH) in situations with a high number of parameters (d > 10), the estimation of the volatility matrix may become infeasible ^[49]. Thus, despite being a popular choice, one limitation of the method is the requirement of a large sample size ^[32].

Furthermore, conditional correlation models have emerged as a more practical alternative for predicting and interpreting parameters ^[53]. In this context, the DCC-GARCH model ^[54] is more realistic than the constant conditional correlation CCC-GARCH model ^[55] as it allows for conditional correlations to change over time. The asymmetric ADCC ^[56] model is an extension of the DCC, enabling the presence of asymmetric dynamic correlations. Finally, the FDCC ^[57] introduces a more flexible parameterization of correlation dynamics by relaxing the equality for all correlations. Numerous examples in the literature confirm the relevance of these models for capturing the dynamic dependence of time-varying correlation coefficients. For instance, ^[58] concludes that DCC models provide a better estimation of the dynamic correlation structure, enabling more efficient capture of volatilities and forecasting of returns than other models.

Motivated by the insights mentioned above, this paper aims to examine the spillover effects on returns and volatility among three prominent energy spot markets: title transfer facility (TTF) for natural gas (NG), Brent crude oil, and the electricity market (EPEX). To achieve this, we employ a two-step approach. First, we use vector autoregressive (VAR) models to identify lagged return effects from one spot market to another. Second, we utilize a set of models belonging to the family of DCC, which has proven to be suitable in previous studies. With these models, we assess the impact on the conditional mean returns and volatility across the spot markets. Despite several papers addressing different types of energy resources, none have comprehensively analyzed the joint impacts on the persistence shocks of NG, oil and electricity spot markets, as presented in this research. We also introduce innovative insights by incorporating recent datasets covering the role of the COVID-19 pandemic crisis and the war in Ukraine on returns and volatilities. In terms of methodology, given the prominence of the family of DCC methods in the literature, we introduce a comparative analysis of results for estimating dynamical conditional correlations, utilizing DCC models and their subsequent extensions: asymmetric (ADCC) and flexible (FDCC). This constitutes an innovation in the literature, especially when considering these three spot markets, which has not been done in the past.

Given the significance of the COVID-19 pandemic and the war in Ukraine, both of which led to unprecedented instability in economies, our study proposes to test the following research hypotheses concerning this topic:

A1: The pandemic crisis had a substantial impact on the returns of the TTF NG, Brent crude oil and electricity EPEX spot markets, but the impact was not uniform across these markets.

A2: The Ukraine conflict extended the influence of the pandemic crisis on the returns and volatilities of these spot markets, albeit with varying degrees of intensity.

The impacts of NG, oil and electricity on other activity sectors are frequently discussed in the literature. This paper also aims to offer new and recent insights by combining these three energy sources. The goal is to provide information for stakeholders in the energy markets regarding the following research hypothesis:

B1: Lagged returns significantly influenced the returns of TTF NG, Brent crude oil and electricity over time.

B2: There was a notable spillover effect on returns and volatility among these spot markets.

C: The persistence of shocks affected the dynamic conditional correlations differently among the spot markets.

As the main empirical findings, this paper reveals the considerable effect of the pandemic crisis and the Ukrainian war on the increase in volatility, but with different impacts on returns among energy sources. This study also highlights the significant effect of previous lagged returns within each market, particularly for Brent oil and electricity. Additionally, it identifies a robust unidirectional positive spillover effect from the Brent oil market to the returns of electricity and NG markets. Finally, the time-varying correlation coefficient of the DCC-GARCH model reveals weak positive autocorrelation between NG and electricity returns. Furthermore, positive shocks to returns had a more pronounced impact on volatility compared to negative shocks across all the time series.

The study is structured as follows: section 2 provides a description of the datasets and the mathematical foundation underlying the empirical models employed. section 3 presents the results, and section 4 summarizes the main conclusions, limitations and potential avenues for future research.

2.   Materials and methods

2.1.   Data

We have curated three distinct datasets, each comprising 153 monthly price records, representing natural gas, oil and electricity from the following sources: TTF NG in the Netherlands, Brent crude oil and electricity from the Germany-Luxembourg (DE/LU) spot market. These datasets cover the period from January 2010 to September 2022, selected to provide an overview of these markets since the beginning of the 2010 decade, shortly after the subprime mortgage crisis ^[59], until the last available data at the time of data collection for our study. The choice of monthly data was based on the periodicity retrieved from Nasdaq Data Link ^[60] and the USA Energy Information Administration (EIA) ^[61], for TTF NG and Brent crude oil, respectively. For consistency of results, we also selected monthly data for electricity from the Energy-Charts ^[62] website. TTF NG, renowned for its high liquidity, is a key player in the European NG market and is primarily traded on the European Energy Exchange (EEX) ^[63]. It distinguishes itself as a prominent NG trading hub in Europe. Brent crude oil, on the other hand, holds substantial global significance and serves as a crucial benchmark for global oil pricing. It is closely monitored by central banks and international institutions ^[64]. Lastly, EPEX SPOT operates day-ahead power markets for various European countries. In our analysis, we specifically focus on electricity prices from the Germany-Luxembourg spot market ^[62], representing this facet of the energy market.

2.2.   Diagnostic tests

Before delving into the empirical models, we conducted a preliminary analysis involving a six-step procedure as follows:

● Return calculation

● Normal distribution check

● Serial data correlation verification

● Correlation analysis over time

● Unit root analysis

● Autoregressive conditional heteroscedasticity (ARCH) effects examination

Initially, we computed price returns from the NG, Brent oil and electricity spot markets. These returns (denoted as 'r') signify the proportion gained or lost (p) since the previous time period. This calculation can be approximated as follows:

This approximation is effective when ${r}_{t}$ is close to zero. Obviously, a possible asset may be risky if its returns exhibit significant fluctuations over time. Market volatility tends to surge when major news or events occur, and it may require several periods for the market to fully assimilate and respond to such developments. In the second step, we examined the normal distribution of each series using the Jarque-Bera (JB) test ^[65]. Rejecting the null hypothesis in this context indicates that a given time series deviates from a normal distribution at a specified critical significance level, typically 0.05. Another crucial aspect to consider is the presence of serial correlation, which can impact the unbiased and consistent estimation of regression model coefficients. In the third step, we employed the Ljung-Box Q test to assess autocorrelation within the series ^[66]. Rejection of the null hypothesis at the 0.05 significance level signifies the presence of serial correlation. Moving on to the fourth step, we employed Pearson's correlation coefficient to evaluate the association between two variables ^[67]. As a fifth step, we conducted tests to check the stationarity of the time series. This is essential to avoid spurious correlations in autoregressive models. We utilized the augmented Dickey-Fuller (ADF) and Phillips-Perron (PP) tests for this purpose. The presence of unit roots in a time series can manifest when there are changes in the mean, variance or autocovariance of its distribution over time ^[68]. The ADF test extends the Dickey-Fuller test by incorporating additional lagged terms of dependent variables to eliminate autocorrelation ^[69]. Rejection of the null hypothesis in both tests indicates that the time series is stationary. Lastly, we investigated the presence of serial dependence (i.e., ARCH effects). To accomplish this, we employed Engle's ARCH test, which is a Lagrange multiplier (LM) test designed to assess the significance of these effects ^[48]. Alternatively, the Ljung-Box Q test can be used with Engle's ARCH test to examine ARCH effects in the first m lags of the squared residual series.

2.3.   Empirical models

ARCH models are frequently used in macroeconomics. For instance, ^[48,70] found evidence that large and small forecast errors may occur in some clusters. The GARCH model introduced by ^[49] is a more robust model by enabling the conditional variance to be dependent on previous lags ^[71]. We implemented a multivariate GARCH model, which has the power to examine returns and volatility linkages ^[72,73,74]. To infer the variance of residuals of VAR (1) and to estimate the dynamic conditional correlation between prices and returns of TTF NG, Brent oil and electricity EPEX spot markets, we use DCC, ADCC and FDCC models. Several studies reveal the ability of this approach to capture spillover effects on returns and volatility ^{[51,53,72,73,74]}.

2.3.1.   VAR

Consider the model with p-order in terms of lags as follows:

where $\delta = {\left({\delta }_{1}, {\delta }_{2}, \cdots , {\delta }_{n}\right)}^{{'}}$ is a vector of the constant terms, $\mathrm{\Phi }$ a matrix of the previous own lag time (t−1) returns and ${h}_{t} = ({h}_{1t}, \cdots , {h}_{nt}){'}$ a vector of the serial uncorrelated error terms that follows $E\left({h}_{t}\right) = 0$, $E\left({h}_{t}{{h}_{t}}^{{'}}\right) = \mathrm{\Sigma }$, and $E\left({h}_{t}{{h}_{s}}^{{'}}\right) = 0$ for $t\ne s$.

We implemented bivariate VAR (1) models that, for the specific case of NG (${r}_{1})$ and oil (${r}_{2})$ returns, can be represented by the following expressions:

where ${\rm{ \mathsf{ ϕ} }}$ is a $2\times 2$ matrix with the terms that indicate the effect of previous time lag returns on the current bivariate returns of the model. To ascertain the presence of serial correlation in the residuals for each of the three bivariate VAR (1) models, we conducted both the Portmanteau test (asymptotic) and Engle's test to detect ARCH effects. To determine the optimal lag order of the VAR model, we use the Hannan-Quinn information criterion (HQIC) and the Schwarz information criterion (SBIC). Additionally, we employed Granger causality tests to determine whether one time series can effectively forecast another. The definition of Granger causality, as proposed by ^[75], holds paramount significance in examining dynamic relationships between time series. It leverages the concept of temporal precedence, distinguishing it from causal notions grounded in controlled variation ^[76]. The null hypothesis of no Granger causality remains unaltered unless and until lagged values of an explanatory variable are included in the regression.

2.3.2.   GARCH

Let ${r}_{t}$ be a $3\times 1$ series of returns of TTF NG, Brent oil and EPEX electricity returns. We specify the mean equation with autoregressive model VAR (1) term of ${r}_{t}$, which can be specified as follows:

The univariate GARCH model is used to derive the expression of residual variances. Following ^[77], we consider that a first order of the GARCH (1, 1) model is sufficient to assess the conditional variance (${\sigma }_{t}^{2}$), which is specified by:

where $\alpha$ and $\beta$ are $3\times 1$ vectors that respectively measure the conditional variance in the ARCH's terms (i.e., the short-term persistence effect) and the conditional volatility in the GARCH's terms (i.e., the long-term persistence effect) ^[73].

2.3.2.1.   DCC-GARCH

The DCC model was introduced by ^[54]. Let ${\mathrm{\Sigma }}_{t}$ represent a $3\times 3$ conditional covariance matrix formally given by ${\mathrm{\Sigma }}_{t} = {D}_{t}{R}_{t}{D}_{t}$, where ${D}_{t}$ is the $3\times 3$ diagonal conditional matrix that includes time-varying standard deviations on the diagonal and ${R}_{t}$ is the time-varying correlation matrix such that:

where ${Q}_{t}$ is a symmetric positive matrix specified as follows:

with $\stackrel{-}{Q}$ materializing a $3\times 3$ unconditional correlation matrix of the standardized residuals ${h}_{it}$. Parameters ${\theta }_{1}$ and ${\theta }_{2}$ are non-negative with a sum less than unity. Under a DCC specification, the typical element of the time-varying correlations will be of the form:

Therefore, ${R}_{t}$ is a matrix of time-varying correlations in which ${\rho }_{ij, t}$ take values of one on its main diagonal:

2.3.2.2.   ADCC-GARCH

The asymmetric dynamic conditional correlation generalized autoregressive conditional heteroskedasticity (ADCC-GARCH) model was proposed by ^[56] to generalize the DCC model by permitting the presence of asymmetric dynamic correlations. This extension is adequate to examine dynamic correlation among different asset classes and investigate the presence of asymmetric responses in conditional variances and correlations to negative returns. Intuitively, it is useful to explain the increase in the conditional correlation during market downturn periods ^[63]. In this new approach, the ${Q}_{t}$ matrix is given as follows:

where the coefficient ${\theta }_{3}$ explains the presence of asymmetric effects. Moreover, $Z = {\xi }_{t-1}{\xi }_{t-1}^{{'}}$ is the covariance matrix of $\left[E\left({\xi }_{t-1}{\xi }_{t-1}^{{'}}\right)\right]$, with ${\xi }_{t-1} = I\left[{h}_{t} < 0\right] \otimes {h}_{t}$. Note that $\otimes$ is the Hamadard product, whereas $I\left[.\right]$ is a function that takes value 1 when the residuals are negative and 0 otherwise.

2.3.2.3.   FDCC-GARCH

The flexible dynamic conditional correlation generalized autoregressive conditional heteroskedasticity (FDCC-GARCH) model proposed by ^[57] relaxes the assumption of equal dynamics for all the correlations by introducing a block-diagonal structure, thereby allowing to extend the original DCC model. Hence, it provides a more flexible parameterization of correlation dynamics, while maintaining the number of parameters at a feasible level. In the FDCC-GARCH model, the ${Q}_{t}$ matrix is given as follows:

where c, a and b are partitioned 3-dimensional vectors with the following structure:

where ${i}_{h}$ is an h-dimensional vector of ones and w is the number of blocks (similarly applied to b and c). The coefficient vectors contain w different coefficients, each of them possibly repeated ${m}_{j}$ times, with j = 1, 2, $\cdots$, w. As a result of the block structure of coefficient matrices, the dynamics are equal only for groups of variables and not for the whole correlation matrix. Finally, Engle's DCC model, whose main innovation is the relaxation of the common correlation dynamics hypothesis among all the assets, can be obtained by considering the following setting:

3.   Results

In this section, we present and analyze the results obtained in our study. In section 3.1, we aim to assess the impacts of the pandemic crisis and the subsequent war in Ukraine on the TTF NG, Brent crude oil and electricity EPEX spot markets, as hypothesized in A1 and A2. We base this assessment on our preliminary analysis of the datasets. Moving onto section 3.2, we utilize the empirical models to investigate the presence of spillover effects on the returns and volatility among the three spot markets, in line with hypotheses B1 and B2. Furthermore, we observe whether the persistence of shocks has led to varying degrees of influence on the dynamic conditional correlations among the spot markets, as posited in hypothesis C.

3.1.   Exploratory data analysis and preliminary statistical tests

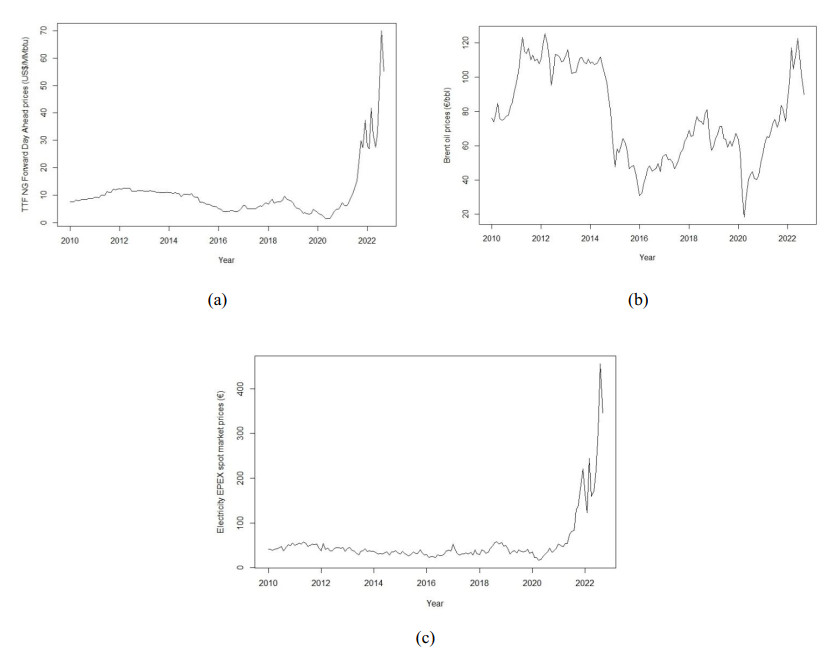
Figure 1 depicts the price trends of TTF NG, Brent oil and the electricity EPEX spot market in Germany-Luxembourg (DE/LU) from January 2010 to September 2022.

These prices followed distinct patterns over time. Initially, there was a gradual price increase until early 2012, followed by relatively stable fluctuations until the first half of 2020. However, a significant shift occurred thereafter, with prices skyrocketing in response to the pandemic crisis and the Ukraine-Russia war. Notably, Brent oil prices exhibit three distinct phases: from 2010 to 2014, prices remained consistently high, mostly above?100. From 2015 to 2020, there was a notable price reduction, with the lowest point reached in the first half of 2020, primarily due to various governmental measures, including lockdowns, which directly impacted lifestyles and reduced crude oil consumption. EPEX SPOT electricity prices remained relatively stable until the first half of 2020, after which they exhibited an exponential growth trend, reaching a peak in the middle of 2022 at?455.38.

Figure 2 presents the monthly returns of TTF NG, Brent oil and the electricity EPEX spot market. While all three series exhibit a mean close to zero, the highest volatility is observed in the returns of NG and electricity, particularly noticeable around late 2019 and reaching its peak negativity in the first half of 2020 during the onset of the pandemic crisis. Electricity returns show relatively consistent variations over time but become more pronounced since the pandemic's outset. Brent oil returns exhibit more uniform variability, ranging between –0.2 and 0.2, with two prominent peaks coinciding with the early stages of the pandemic crisis in the first half of 2020. These observations are further corroborated by the monthly squared returns, as shown in Figure S1 in the supplementary. Notably, both the pandemic crisis and Russia's invasion of Ukraine significantly impacted the increase in return volatility, especially evident for TTF NG (since early 2020), Brent oil (with a substantial peak in the first half of 2020) and electricity, which became even more pronounced since early 2022.

Table 1 provides a summary of descriptive statistics for NG, Brent crude oil and electricity prices, as well as their corresponding returns. The results highlight that the standard deviation was highest for electricity prices, exceeding the mean price. The standard deviation for NG was also relatively close to the average, aligning with the exponential variations observed since 2020. Minimum and maximum price points for all three series occurred in the pre-pandemic and post-pandemic crisis periods.

Regarding returns, the data confirm the higher volatility of electricity compared to the other energy sources, with a standard deviation of 0.177, followed by NG and oil, with values of 0.137 and 0.113, respectively. Except for oil, all series exhibit positive skewness tails, with higher skewness values for NG and electricity due to extreme price movements since 2020. Moreover, except for oil prices, all other series display kurtosis values exceeding the reference range for normally distributed data (between –2 and 2). Figure S2 presents the distributions of all series. NG, Brent oil and electricity returns exhibit more symmetric distributions when compared to the price series. The results of the Jarque-Bera test, conducted with a significance level of 0.05, indicate that none of the price and return series follow a normal distribution. Among the series, electricity returns (JB = 7.611, p-value = 0.222) and Brent crude oil prices (JB = 7.666, p-value = 0.008) display relatively minor deviations from normality.

The assessment of serial correlation holds utmost significance in preventing the occurrence of spurious regressions within the empirical models proposed in this study. Table 1 additionally presents findings indicating that electricity returns stand as the sole series lacking significant serial correlation (Q = 16.275, p = 0.092). Figure S3 furnishes supplementary insights via autocorrelation function (ACF) plots. These plots serve as valuable tools in identifying discernible patterns and deviations from randomness within price series. It is worth noting that NG returns exhibit values exceeding predefined bounds at multiple lags, thereby contributing to the rejection of the white noise assumption and, consequently, indicating the presence of autocorrelation. Furthermore, the outcomes of unconditional cross correlations provide substantial insights. Notably, a strong positive correlation is evident between NG and electricity price series (r = 0.958, p-value < 0.001). This is followed by a moderate correlation between NG and oil returns (r = 0.457, p-value < 0.001), and a weak correlation between oil and electricity prices (r = 0.278, p-value < 0.001). Additionally, based on the results of Pearson's coefficient with a significance level of 0.05, we can assert the absence of a significant association between NG and Brent oil returns. While the correlation between NG and electricity returns exhibits the highest values, it still represents a moderate correlation (r = 0.516, p-value < 0.001), whereas the correlation between oil and electricity returns indicates a weak relationship (r = 0.211, p-value = 0.007).

Subsequently, we proceeded with unit root tests to assess the stationary condition, a prerequisite for applying an autoregressive process in our empirical return models. The results of ADF and PP tests are presented in Table 2. Both tests consistently indicate that NG, crude oil and electricity prices exhibit nonstationary behavior. This observation aligns with the price trends depicted in Figure 1, emphasizing that the data undergoes clear changes over time. To address this nonstationary behavior and achieve stationary processes, we computed the first difference values, representing changes from one period to the next (Figures S4a, b and c). The evolving trends confirm that the first differences I (1) of all price series now exhibit variations around a mean of zero. Specifically, the first differences in crude oil prices reveal relatively consistent variance over time, while NG and electricity I (1) prices display higher variation, particularly in recent years since the onset of the pandemic crisis and the Ukrainian war.

As for returns, the outcomes of the ADF and PP tests affirm that both the return levels and first difference series for NG, crude oil, and electricity are stationary, with p-values < 0.010. This alignment is consistent with the trends observed for each series in Figure 2, where variations center around zero. Notably, variability over time appears to be less stable for NG and electricity returns, particularly since the third quarter of 2021. Nevertheless, the first differences for return processes remain stationary. Figures S4d, e and f further illustrate the relatively consistent variance in crude oil returns, whereas NG and electricity exhibit more pronounced variation, particularly with elevated values since 2022. Figure S4e additionally highlights a peak in crude oil returns at the onset of the COVID-19 pandemic in the first half of 2020.

Hereinafter, the focus of the analysis is restricted to NG, crude oil and electricity returns, which will be used in the empirical models outlined in section 2.3. To this end, we initiated an examination of the existence of ARCH effects to determine whether variances in these series exhibit temporal variation. Table S1 presents the outcomes of Engle's ARCH and the Ljung-Box tests, which assess the time-varying conditional variance of squared residual errors (h²) within the dynamic models for return series. Both tests consistently indicate highly significant ARCH effects in all series. These findings align with the observed variations in squared residual errors generated by the dynamic models, as depicted in Figure 3. Notably, there is clear serial correlation in h² for all series.

For NG, distinct clusters of conditional volatility can be identified. First, there is a period until 2015 characterized by relatively small variation. From 2015 until the pre-pandemic phase, volatility began to increase. Finally, starting from that moment, there is a substantial change in variability. During this period, a reduction in residuals to values similar to the second cluster can be observed around the beginning of 2021 (Figure 3a).

In the case of Brent oil, volatility remains relatively consistent over time but exhibits clear autocorrelation in squared residuals. Once again, a peak in volatility is evident in the first half of 2020.

In relative terms, volatility in electricity EPEX returns surpasses that of NG and Brent oil, with h² fluctuating between 0 and 0.1 until the onset of the pandemic in 2020, at which point the first peak above 0.2 emerges. Subsequently, volatility decreased but started rising again following Russia's invasion of Ukraine in 2022.

Lastly, Pearson's coefficients reveal the extent of correlation among the series. Notably, NG and electricity exhibit a higher correlation (r = 0.479, p-value < 0.001), representing a moderate association. This is followed by the correlation between NG and oil (r = 0.229, p-value = 0.004), which is very weak. The correlation between oil and electricity is not significant (r = 0.07, p-value = 0.372).

3.2.   Parametric analysis: links between returns and volatility among TTF NG, Brent oil and EPEX electricity (spillover effects)

In this section, we unveil the outcomes of the empirical models we employed. Initially, we conducted separate bivariate VAR models to examine potential effects of lagged returns from one market on another (hypothesis B1). Subsequently, we employed a series of DCC-GARCH models to delve into the repercussions on the conditional mean returns and volatility across the markets (hypothesis B2). Furthermore, we explored the dynamic conditional correlations between these markets, characterized by varying intensities (hypothesis C).

3.2.1.   VAR models applied to returns

Table 3 displays the parameters of the bivariate VAR (1) model employed to estimate mean returns. For each model, we have constant terms represented by δ₁ and δ₂ for spot markets 1 and 2, corresponding to TTF NG and Brent crude oil returns in the first model, TTF NG and electricity EPEX (DE/LU) returns in the second model and Brent oil and electricity EPEX returns in the third model. The terms Φ₁₁ and Φ₂₂ signify the autocorrelation in returns based on the previous lag (t−1) for the considered spot markets within each of the three VAR (1) models. We explored various lag orders, but since many terms were not statistically significant, we did not include them in our study. Finally, Φ₁₂ and Φ₂₁ represent the return spillovers between the spot markets.

The results of the first model reveal a significant impact of NG and Brent oil's own lagged returns on their current returns (Φ₁₁ = 0.219, p-value = 0.006; Φ₂₂ = 0.286, p-value < 0.001). Regarding the spillovers between these two markets, only the current NG returns were positively influenced by the previous lagged returns (t−1) of oil (Φ₁₂ = 0.322, p-value < 0.001). Granger causality tests also confirm the positive impact of the Brent oil market on TTF NG returns (G = 11.793, p-value < 0.001). Figure S5a visually illustrates this impact, with confidence interval bounds above the horizontal line $y = 0$. A diagnostic analysis of the VAR (1) residuals suggests that they can be considered white noise (P = 56.283, p-value = 0.102) but it also indicates the presence of ARCH effects, which will be investigated in section 3.2.2.

The second model reveals the existence of autocorrelation between the previous own lagged returns for NG and electricity (Φ₁₁ = 0.195, p-value = 0.037; Φ₂₂ = –0.297, p-value = 0.002). There was a weak positive autocorrelation between the lagged TTF NG returns and current EPEX electricity returns (Φ₂₁ = 0.213, p-value = 0.078). Granger causality tests also suggest a weak positive effect of NG on electricity returns (G = 3.144, p-value = 0.077). Although the diagnostic analysis of residuals reveals the presence of serial correlation in this bivariate VAR (1) model (P = 65.648, p-value = 0.019), the results of the HQIC (–2.131) and SBIC (–2.059) information criteria confirm one period as the optimal lag order for this bivariate model (Table S2). The limited impact of NG on electricity is depicted in Figure S5b.

Table 3 also confirms the significant effect of lagged returns on current returns for Brent oil and electricity EPEX spot markets (Φ₁₁ = 0.300, p-value < 0.001; Φ₂₂ = –0.266, p-value = 0.001). There was also a unidirectional return spillover from the Brent oil market to the electricity EPEX market (Φ₂₁ = 0.389, p-value = 0.002). The bivariate residuals suggest serial correlation (P = 40.894, p-value = 0.606) and the presence of ARCH effects (LM = 207.430, p-value < 0.001). The Granger causality test also indicates a positive effect of the oil market on electricity returns (G = 9.748, p-value = 0.002), as shown by Figure S5c). These results suggest the possibility of a simultaneous impact of the Brent oil spot market on TTF NG and EPEX electricity markets. This assumption is substantiated by the results of Table S3 after applying a trivariate VAR (1). In this model, current returns (t) for each spot market are determined by the immediate lags (t−1) of three variables (NG, Oil, and Electricity). The results confirm a positive autocorrelation between oil and NG (Φ₁₂ = 0.313, p-value = 0.001) and oil and electricity (Φ₃₂ = 0.391, p-value = 0.002). There is also a significant effect of own lagged returns on returns for NG, oil and electricity. Furthermore, the results demonstrate that the model residuals do not exhibit serial correlation (P = 119.51, p-value = 0.079), and they indicate the presence of ARCH effects (LM = 651.28, p-value < 0.001). Both HQIC (–3.723) and SBIC (–3.578) information criteria also suggest a lag of one period as the optical order (Table S4). Finally, Granger causality test results reveal a significant unidirectional effect of the Brent oil market simultaneously on TTF NG and EPEX electricity markets (G = 6.743, p-value = 0.001).

3.2.2.   GARCH models applied to conditional returns and volatility

Table 4 presents the results for all DCC-GARCH models, which produced similar outcomes. Consequently, we decided to use the DCC model estimates for the remaining analysis, as they correspond to the simplest model and yielded the lowest AIC value (–4.550). We also considered that the asymmetric term for DCC is not significant (${\theta }_{3} < 0.001$, p-value $\approx 1$), and FDCC did not provide better results than the DCC method. The results indicate that the conditional mean returns (η) were not statistically significant for any of the markets, with values close to zero. The δ terms represent the short-term persistence of returns in the VAR (1) models. Except for TTF NG, Brent oil and electricity EPEX, the previous own lagged returns were statistically significant for the current returns (t) (${\delta }_{oil}$ = 0.192, p-value = 0.018; ${\delta }_{elect}$ = –0.259, p-value = 0.001). The parameter $\alpha$ reflects the effect of unexpected news or shocks, while the parameter β captures the effect of lagged conditional variance in NG, oil and electricity markets, corresponding to the long-term persistence of volatility. Strong evidence exists for the positive impact of the short-term persistence effect of the previous own conditional variance on the current returns for TTF NG (${\alpha }_{NG}$ = 0.195, p-value < 0.001) and Brent oil (${\alpha }_{oil}$ = 0.732, p-value = 0.006) spot markets. Additionally, there is a significant positive long-term volatility persistence for NG (${\beta }_{NG}$ = 0.804, p-value < 0.001), oil (${\beta }_{oil}$ = 0.251, p-value = 0.012) and the electricity EPEX market (${\beta }_{elect}$ = 0.915, p-value < 0.001). In this context, long-term volatility persistence corresponds to the effect of the previous own conditional variance on the current one, meaning that positive shocks (or news) on returns have a greater impact on volatility than negative shocks for all the time series. Furthermore, the sum of the ARCH (α) and GARCH (β) coefficients for all return series is less than unity, indicating volatility clustering in all variables, which aligns with the conclusions drawn from Figure 3. As we can observe, ${\beta }_{oil}$ shows low values associated with a higher ${\alpha }_{oil}$, which can occur in some circumstances. According to ^[78], this leads to GARCH volatilities that are spikier than those with relatively low alpha and relatively high beta. This may be attributed to GARCH volatilities with high volatility-of-volatility (vol-of-vol). Further research should be conducted for a better understanding of long-term volatility persistence compared to other types of models.

The shape's term ($\lambda$) represents the degrees of freedom in the t distribution and is statistically significant only for NG ($\lambda$ = 4.189, p-value < 0.001). Finally, ${\theta }_{1}$ and ${\theta }_{2}$ denote the dynamic correlations of the series. ${\theta }_{1}$ represents the short-term shock persistence among the conditional correlations of the markets, while ${\theta }_{2}$ gives the long-term persistent shock effect on the conditional correlation of the markets. Both terms are statistically significant and positive (${\theta }_{1}$ = 0.043, p-value = 0.001; ${\theta }_{2}$ = 0.936, p-value < 0.001), indicating significant short and long-term correlations among the markets. The sum of coefficients is less than one, suggesting dynamic conditional correlation as mean-converging. Table S5 reports the bivariate DCC-GARCH models, providing pairwise comparisons between the three series. The results closely resemble those obtained using the trivariate setting presented in Table 4. However, new terms for dynamic correlation between TTF NG, Brent oil and electricity EPEX markets are now obtained. The results reveal significant short-term persistence of shock in the dynamic conditional correlation between the TTF NG and EPEX electricity spot markets (${\theta }_{1}$ = 0.102, p-value = 0.001). Regarding long-term persistent shock effects, there was high significance in the dynamic conditional correlation between NG and Brent oil (${\theta }_{2}$ = 0.930, p-value < 0.001), NG and electricity EPEX (${\theta }_{2}$ = 0.889, p-value < 0.001) and Brent oil and electricity EPEX (${\theta }_{2}$ = 0.919, p-value = 0.029) spot markets.

Finally, Figure 4 displays the dynamical conditional correlations between pairs of spot markets. The lines represent the linear dynamic correlation averaged over time. The DCC between NG and oil fluctuates between –0.10 (very weak correlation) and a weak correlation of 0.25, resulting in a global dynamic correlation of approximately 0.086 with a null slope (Figure 4a). The DCC between TTF NG and electricity EPEX (DE/LU) spot markets exhibits the highest variations, ranging from a negative very weak correlation (ρ = –0.176) to a strong correlation (ρ = 0.624). Essentially, the DCC slightly decreased until 2015 and began increasing from that point, reaching its highest correlation in September 2022 (Figure 4b). Lastly, the DCC between Brent oil and electricity EPEX shows more significant fluctuations, varying from a minimum negative correlation (ρ = –0.029) to a weak correlation of 0.332, with a negative average trend (slope = –0.001) (Figure 4c). In terms of evolution, we can identify three main clusters: the first with a weak correlation (between 0.120 and 0.332) until early 2014, followed by a period of decreased correlations until 2019, and finally, since the first quarter of 2020, DCC has become more similar to the first period.

4.   Conclusions

This study aimed to analyze the evolution of three spot markets: TTF natural gas, Brent crude oil and electricity EPEX of Germany-Luxembourg (DE/LU). It focused on three main aspects outlined in hypotheses A, B and C. As major contributions to the energy literature, we highlight the joint analysis of these energy markets in terms of spillover effects on returns and the implementation of a set of dynamical conditional correlation methods (DCC, ADCC and FDCC) for modeling the repercussions on the conditional mean returns and volatility across these markets. Our study also includes recent datasets that allowed us to analyze the impacts of COVID-19 and the subsequent war, representing a new advance in knowledge about these spot markets.

Firstly, the study investigated the impact of COVID-19 on return volatility and how the Russian invasion of Ukraine might have extended this impact (hypothesis A1). The analysis revealed that the COVID-19 pandemic crisis had a strong effect on the exponential growth of prices and an increase in volatility. However, this effect was not uniform across the return series. While prices for all spot markets increased since the first quarter of 2020, Brent oil prices returned to pre-pandemic crisis levels, whereas TTF NG and electricity EPEX prices continued to increase exponentially, reaching their highest values by the beginning of the third quarter of 2022. From this point, prices began to gradually decrease. However, when examining returns, it was evident that volatility increased from the beginning of 2020 until the end of the study for NG and electricity EPEX, while for Brent oil, there was only a significant peak in the first quarter of 2020. Therefore, the war in Ukraine did not have the same impact on each series (hypothesis A2). Intuitively, this means that both hypotheses were validated.

The study also revealed that lagged returns from previous periods for Brent oil and EPEX electricity had significant impacts on current returns (${\delta }_{oil}$ = 0.192, p-value = 0.018; ${\delta }_{elect}$ = –0.259, p-value = 0.001). Moreover, the results of the VAR (1) models indicated that lagged returns for TTF NG also had an impact on current returns (hypothesis B1). Regarding possible spillover effects on returns and volatility among markets, as raised in hypothesis B2, the results showed a strong short-term persistence effect of the previous own conditional variance for TTF NG (${\mathrm{\alpha }}_{NG}$ = 0.195, p-value < 0.001) and Brent oil (${\mathrm{\alpha }}_{oil}$ = 0.732, p-value = 0.006) spot markets. Additionally, positive shocks on returns were found for NG (${\beta }_{NG}$ = 0.804, p-value < 0.001), oil (${\beta }_{oil}$ = 0.251, p-value = 0.012) and electricity EPEX markets (${\beta }_{elect}$ = 0.915, p-value < 0.001).

Finally, this study confirms that shock persistence affected the dynamical conditional correlations between spot markets in different ways (hypothesis C). Results showed that long-term persistent shock effects highly affect the dynamic conditional correlation between NG and Brent oil (${\theta }_{2}$ = 0.930, p-value < 0.001), NG and electricity EPEX (${\theta }_{2}$ = 0.889, p-value < 0.001) and Brent oil and electricity EPEX (${\theta }_{2}$ = 0.919, p-value = 0.029) spot markets. However, there was only a significant short-term persistence of shock in the dynamical conditional correlation between the NG TTF and EPEX electricity spot markets (${\theta }_{1}$ = 0.102, p-value = 0.001). By analyzing DCC coefficients, it was concluded that the highest DDC occurred between TTF and electricity EPEX (DE/LU), ranging from a very negative, very weak correlation to a strong correlation over time. During the pandemic crisis and the war in Ukraine, this correlation remained strong, reaching a peak in this period.

While this study contributes to the energy literature, future research should consider extending the series to include other NG, oil and electricity spot markets to investigate potential differences among them and validate the results presented here. Additionally, expanding the dataset to include periods before 2010 would allow for a comparison of return evolutions and volatility during different shock periods. Finally, it is important to address the limitations of this research, including difficulties in accessing open data and the inability to relate NG, oil and electricity prices to other indicators that may directly impact returns and volatility.

Acknowledgements

FCT projects DSCAIPA-CS-0086-2020, UIDB/04105/2020 and UIDP/04105/2020.

Conflict of interest

The authors declare that there are no conflicts of interest in the execution and publication of this work.

Author contributions:

Gustavo Soutinho was responsible for data collection, analysis, methodology development, and the initial draft of the manuscript. Vitor Miguel Ribeiro wrote the final version of the manuscript, supervised the analysis and the methodology development, and secured funding for the project. Isabel Soares played a crucial role in reviewing the work, supervising the research, and securing funding for the project.