Optimal PMUs placement considering ZIBs and single line and PMUs outages

1.   Introduction

Phasor measurement units (PMUs) based on the global positioning system (GPS) technique are considered to be key elements which are widely used in monitoring, controlling and state estimation of electrical power systems. PMU provides electrical power engineers with precise and immediate information about system states, as its measurements are being on the same datum of time that is defined by GPS. Stability and reliability of power system could be improved by applying synchronized measuring of phasors in several regions of electric power system like control, protection, estimation of system states and voltage fall downs ^[1]. It is unattainable to install PMU at all power system buses because of high cost and connection complexity. Hence, optimal PMUs placement (OPP) problem is required to be solved for better saving and full system observability. So, the capability of PMU to monitor the voltage of system bus and current phasors of its incident lines, requires to locate PMUs at the most appropriate buses to make the system full observable by using less PMUs. Full observability is obtained by monitoring the buses voltage and lines current of the system ^[2].

Recently, many different methods have been presented to identify the solution of PMUs allocations problem. Binary Integer Programming method is presented in ^[3] for PMUs allocation and flow measurements of faults in electrical power systems. Initially, the nonlinear programming problem formulation was unsolvable. So, its initial formulation results were transformed through Boolean implications to a corresponding integer-linear programming (ILP) problem. This transformation provided a high range of scalability. A modified version of binary cuckoo optimization algorithm (BCOA) was introduced in ^[4] to identify the solution of OPP problem. The algorithm structure is mainly based on the lifestyle as well as egg laying of the cuckoo bird. Major features of modified binary cuckoo optimization algorithm (MBCOA) were its capability to obtain the optimum solution and its fast convergence. All stages of cuckoo optimization algorithm (COA) consists of initial population generation, egg number, radius of egg laying and also immigration technique were rearranged in MBCOA to consider the binary form of OPP problem. In ^[5], authors considered hidden critical cost while presenting PMUs placement. In ^[6], authors presented Depth First Search (DFS), Simulated Annealing (SA) and minimum spanning tree methods to solve OPP problem at normal operation condition also under contingencies. In ^[7] the researchers proposed a binary search algorithm for system observability, that is able to find the global optimum solution, but it is computationally expensive. Furthermore, integer programming was used for problem of PMUs placement ^[8,9,10,11], where in ^[8], authors proposed integer quadratic programming, considering loss of PMUs and single line outages. However, the effect of zero-injection buses is not considered in the developed algorithm. The researchers in ^[9] used a generalized integer linear programming. The method considered power systems with and without the existence of conventional flow measurement; nevertheless, some modifications were done to use it in multi-stage planning. Furthermore, it did not study the contingencies. In ^[10], the authors have formulated the multi stage PMUs allocation using ILP. The failure of single PMU is incorporated while the loss of system line outage, is not considered. The authors proposed a binary integer linear programming (BILP) in ^[11] with two objectives, which are minimum metering economy and power system observability. In ^[12], the researchers have introduced an algorithm to solve this problem to achieve the system observability and detect the bad data. In ^[13] the authors have solved OPP problem using a mixed integer nonlinear programming (MINLP) algorithm with variables as binary values variables the observability check is done every time. In ^[14], the authors have solved the OPP based on the rules of topological observability and the ZIBs are taken into account. In ^[15], a genetic algorithm (GA) has been proposed to find the OPP. The authors extended the OPP problem formulation and defined new concepts which are maximizing measurements increase and observability assessment, for normal condition and contingencies. Moreover, the pre-allocation of PMUs is taken into account. The fuzzy algorithm is presented to find the solution of OPP problem with taking into account the lower number of PMU channels for achieving network full observability ^[16], this algorithm is used with normal operating conditions and system contingencies. The recursive tabu search (RTS) is a combination of numerical method and tabu search (TS) has been introduced in ^[17] to obtain a full observable power system with maximum measurement redundancy. A technique introduced in ^[18] for PMUs placement in multiple stages ensured complete system observability under a line loss or PMU failure. The proposed method is based on ILP and multi-criteria decision-making (MCDM) approach. The number of PMUs is identified by ILP for the complete observable system while MCDM has been used to prioritize the optimal locations of PMUs. A novel approach for state estimation of power system using optimal PMUs placement, is proposed in ^[19]. The optimal PMUs placement for full power system observability has been achieved using improved particle swarm optimization (IPSO). This paper has introduced an optimization technique for the state estimation measurements using the weighted least square (WLS) method. Also, it has proposed a numerical method to check the complete system observability that has been fulfilled. In ^[20,21], the authors have presented a flexible and simple, semi-definite programming (SDP) method, which minimizes installed PMUs number, ensures full observability of the power system with considering the availability of traditional measurements. The optimal solution is gotten by the minimization of the objective function with using the decision variables in binary form, subjected to inequality constraint that represents the observability.

In this paper, a modern optimization method which is a flower pollination algorithm (FPA), is adopted to find optimal PMUs placement (OPP) in which its robustness and efficiency as an optimization method is proven. The FPA is utilized to obtain the minimum number of PMUs needed to make the power system completely observable and increase measurements redundancy. The OPP problem is formulated to consider the practical and technical issues in reality. The proposed method has been tested with various cases that are normal case, loss of PMUs, single line outage and considering the existence of zero-injection buses (ZIBs) which helps in reducing the number of PMUs needed to verify the complete observability of the power system. Efficiency, robustness and performance of the proposed method have been practiced on IEEE 14-bus, 30-bus, 39-bus, 57-bus, and 118-bus test systems. The results verify the applicability of the proposed method to solve OPP problem in modern power systems considering the most severe technical issues in reality. The main novel, contributions of this paper are:

ⅰ)Proposing FPA for solving practical optimal phasor measurement unit placement problem.

ⅱ)The proposed method is applicable to large scale power systems with different topologies.

ⅲ)The proposed method considers all contingency issues such as loss of PMUs and line outages.

The rest of the paper is arranged as: section 2 introduces observability analysis and PMUs placement rules at various conditions. The problem formulation of PMUs placement and modeling of ZIB in the power system are discussed in section 3. The suggested optimization method (FPA) is explained briefly in section 4. Section 5 discusses different test cases of PMUs placement and their simulation results for different test system used. Finally, the conclusions of this work are provided in section 6.

2.   Observability analysis and PMUs placement

2.1.   Observability analysis

The main reason of optimal allocation of PMUs in electrical power systems is the observability of the power system which means that all voltage phasors of system buses and all current phasors of system lines are known. Whatever the used method, the power system observability should be checked each time PMU is placed. If the system is observable, the placement process stops, else the process must be continued.

There are two methods for system observability analysis, topological observability and numerical observability. In the topological observability method, the decision is based on logical operation. So, some information about network topology and connection and measurement types with their locations are essential. The power system is observable when the spanning tree can be constructed and full ranked by current measurements set. It uses a graph theory and decoupled measurement model. Numerical observability is based on the numerical factorization of the gain matrix or measurement Jacobian of measurements information. The system is observable when at least one of the matrices has full rank. It uses either decoupled or fully coupled measurement models.

where:

Z: a column vector of length m,

H: Jacobian matrix with size m × (2N – 1)，

x: a column vector of length (2N – 1),

V: a column vector of length m and represents the measurement noise，

N: represents the buses number，

m: represents the measurement samples，

In large systems, these matrices are complicated so the numerical algorithms are not appropriate.

2.2.   PMUs placement rules

The full observability of a system is achieved if all system buses are observable. A bus is observable when its voltage phasor is directly or indirectly measured.

In this work, the topological observability method is used to help in solving the PMUs placement according to following rules.

○ The bus with an installed PMU has its voltage and the current phasors of all its incident branches measured by PMU. This is called direct measurement.

○ For the buses which are connected to a bus with PMU, as the voltage and current phasors are known at one end, ohm’s law is utilized to find the voltage phasor of that bus. This is called pseudo-measurements.

○ If the voltages of two ends of a branch are known, ohm’s law is utilized to find the current between these two ends

A zero-injection bus (ZIB) is another factor which can help in reducing the number of required PMUs to make the power system fully observed. ZIB is a bus that has neither power generator to inject power in it, nor loads to consume power from it. Hence, the sum of all current phasors of its incident branches equals zero. Power system observability will be assessed with the existence of ZIBs using the below rules:

● When an observable ZIB has observable adjacent buses except one, the Kirchhoff’s current law (KCL) and Kirchhoff’s voltage law (KVL) can be applied at ZIB to make this bus observed.

● When ZIB is not observable and it has an adjacent observable buses, KCL and KVL can be applied to make ZIB observable.

● Finally, the node voltage equation is used to make group of ZIBs to be observable if they have adjacent observable buses.

3.   Problem formulation and ZIB modeling

3.1.   PMUs placement problem formulation

The objective of solving the OPP problem is to find the minimum number of PMUs needed and their locations for achieving full observability of the power system. Thus, this objective function is formulated as follows:

where

N: number of buses,

X: the decision vector with binary values,

x_i: an element in X and it show the feasibility of installing PMU at the ith bus as:

A is the binary bus connectivity matrix, and Eq 5 is used to define its entries.

where AX is a set of constraints that show the bus observability where its element is one if the bus is observable and otherwise is zero and b is a vector filled with ones which ensures the observability of the system and is given by:

There is another factor that is very useful because with increasing it, the bus remains observed if one of measurements lost. This factor is called the measurement redundancy and is defined as how many times the bus is observed by direct or indirect measurements. During optimization process to fulfil the objective function, the results give multiple solutions with multiple redundancy measurements for each solution. The decision is to choose the optimal solution that fulfils the objective function and with maximum redundancy. There is a term called redundancy index (R. index) that is used to identify the measurement redundancy. R. index is defined as sum of all buses observability as follows

3.2.   Modeling of ZIBs

The proposed method includes the action of merging ZIB with its incident bus. This merging action helps in reducing system buses by one, and this will help in decreasing PMUs number that are required to fulfil the complete observability of power system states. Moreover, the merging process causes modifications in the network topology of the power system and it needs to redefine the network equations to reflect that changes.

The results obtained by using the merging process change for each bus available to be merged with ZIB. The following are rules of the merging process:

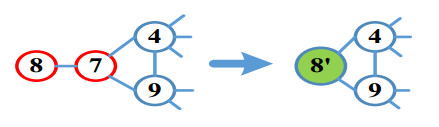
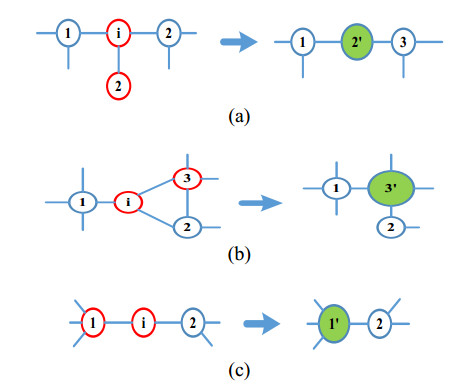
○ Merge ZIB with its incident radial bus, Figure 1(a) shows the merging between ZIB which is incident to radial bus.

Figure 1.  Zero injection buses modeling: a) the first rule of ZIB modeling, b) the second rule of ZIB modeling, and c) the third rule of ZIB modeling.

DownLoad: Full-Size Img PowerPoint

○ The adjacent bus of ZIB which has the greatest number of connected buses is merged with ZIB as shown in Figure 1(b).

○ ZIB is merged with neighbor bus of the greatest number of connected buses. Figure 1(c) shows this rule.

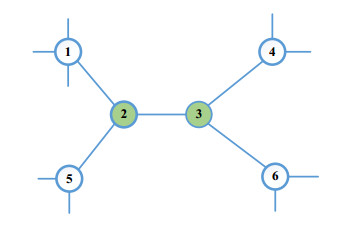
Figure 2 shows a sample network, which is part of a larger system. In this network, the buses 1, 4, 5 and 6 are observable by indirectly method. Buses 2 and 3 are a group of adjacent zero injected buses and their phasors can be computed using KVL and KCL equations as follows:

Figure 2.  A sample group of zero-injected buses.

DownLoad: Full-Size Img PowerPoint

Using Eqs 8 and 9, the voltages V₂ and V₃ can be computed if the voltages V₁, V₄, V₅ and V₆ are known.

4.   The proposed optimization method

4.1.   Flower pollination algorithm

The flower pollination algorithm (FPA) is a meta-heuristic search algorithm that was developed recently by Xin-She Yang and Deb ^{[22,23,24,25]}. It is inspired by the sexual reproduction of flowering plants through pollination process. For simplicity, the four rules are used as follows. First rule: global pollination is represented in cross- pollination and biotic pollination and motion of pollinators obeys Le´vy flights. Second rule: a combination of self-pollination and abiotic pollination represents local pollination. The process does not need any pollinators. Third rule: pollinators improve flower stability. Flower stability is equal to reproduction probability. This probability depends on the resemblance of two involved flowers. Rule 4: switching between local pollination and global pollination is achieved by changing the probability switch, p ∈[0, 1].

The previous rules should be formulated into suitable equations. Thus, in the global pollination rule, pollinators load flower pollen gamete. So, the pollen is moving over long distances. Subsequently, the global pollination with flower stability rules is formulated as:

where X_i^t is a vector represents the pollen i or the solution x_i at the t iteration and g_* is the optimal solution found among all solutions at the current generation/iteration.

L is a Lévy flights based step size which correspond to the pollination strength. As long distance can be wrapped through many distance jumps, A Lévy flight is utilized to simulate efficiently the characteristic. Where, L > 0 is taken from a Lévy function.

where γ is a rescaling coefficient, Γ(λ) is gamma function, and this distribution is suitable for large steps S > 0. S₀ is the initial step size. Two Gaussian distributions U and V are used to draw the step size S by using Mantegna algorithm by the following transformation:

U~N(0, σ²) denotes that Gaussian normal distribution is used to draw the samples that have zero mean and their variance is σ².

The equation of variance calculation is:

(14)

To find local pollination, second and third rules are used to formulate the following:

where x_j^t and x_k^t are pollens of various flowers that have the same plant types and ε is selected from the uniform distributed range [0, 1].

4.2.   Implementation of FPA

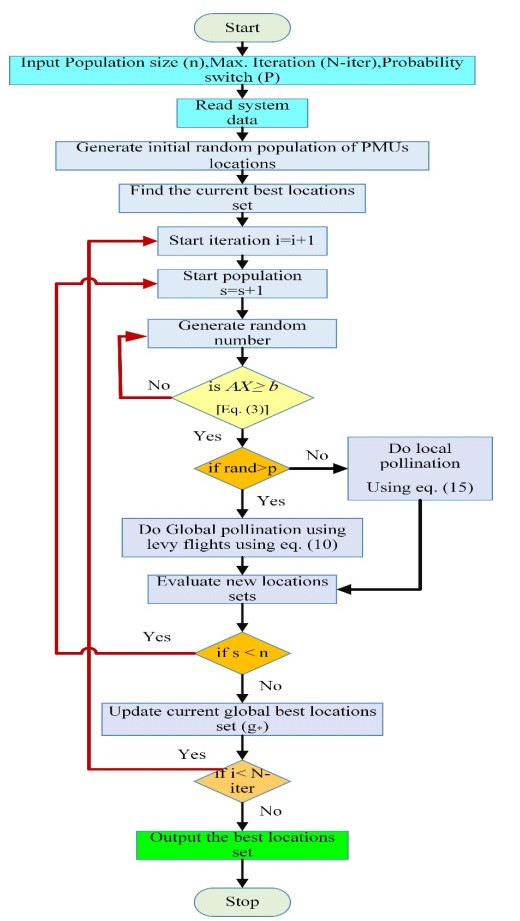
Flower Pollination Algorithm (FPA) is improved by the concept of sexual reproduction of flowering plants via pollination process. In this algorithm, two parameters, population dimension n, and probability coefficient p∈[0, 1] are used to improve the performance of FPA. The moment that n is fixed, p can essentially controls the balance of randomization, pollinators and the local search. Hence, few parameters make the algorithm potentially more generic and less complex. In this paper, the population size n = 20, rescaling coefficient γ = 1.5, the probability p = 0.8 ^[22] and the maximum iteration = 500. The flowchart of the proposed FPA is shown in Figure 3. For each generated solution, before applying this solution, the constraint expressed in Eq 3 must be verified. If this solution does not verify the constraint, this solution is escaped and another solution is generated and this is explained in the following flow chart.

Figure 3.  Flower pollination algorithm flowchart.

DownLoad: Full-Size Img PowerPoint

5.   Simulation results and discussions

5.1.   Test systems

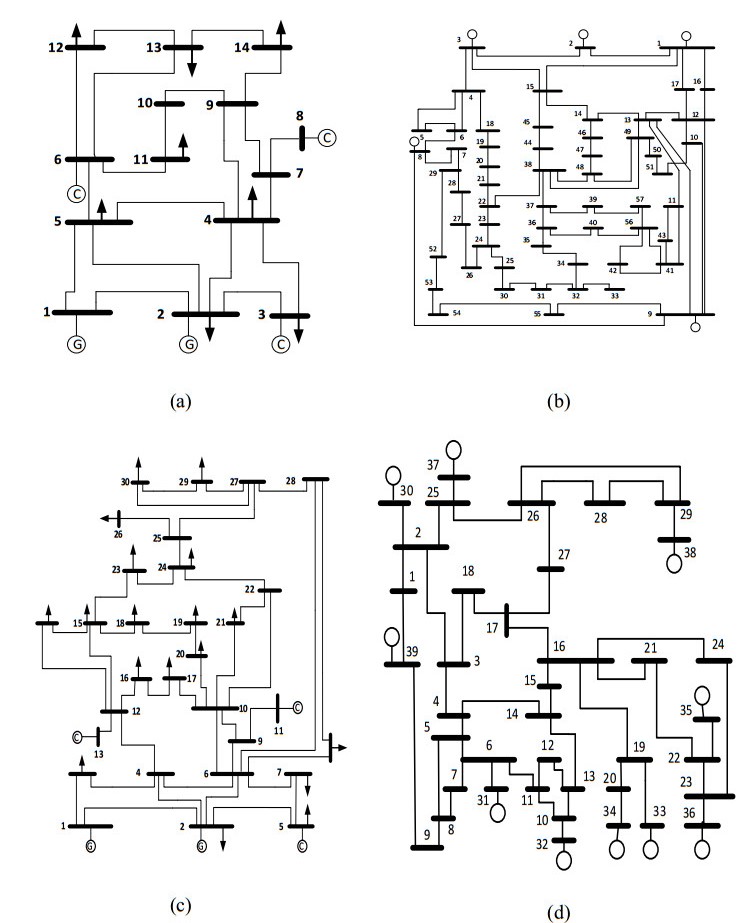
The performance of the proposed method is assessed by applying it on different standard networks such as IEEE 14-bus, IEEE 30-bus, IEEE 57-bus, IEEE 118-bus ^[25], and the New England 39-bus networks ^[26] to find the optimal solution of OPP. Figures 4 depicts single line diagrams of these standard networks. Table 1 shows the number and locations of the zero-injection buses and radial buses for each test network. All the test networks contain two types of synchronous machines; synchronous generators and synchronous motors work as synchronous condensers. Where 14-bus network contains two synchronous generators and three synchronous condensers and its single line diagram is shown in Figure 4(a). 30-bus network contains two generators and four synchronous condensers used for supporting reactive power, and the other two are used for generation and its single line diagram is shown in Figure 4(c). the 57-bus system has four generators and three synchronous condensers and its single line diagram is shown in Figure 4(b). NE 39-bus system has 10 synchronous machines which are generators. Its single line diagram is shown in Figure 4(d). IEEE 118-bus system consists of 54 synchronous machines, 20 of which are synchronous compensators used only for reactive power support and 15 of which are motors, and the other 19 are generators where its single line diagram is given in ^[26].

Figure 4.  Power systems under investigation: a) IEEE 14-bus system with 7 as ZIB and radial bus 8, b) IEEE 57-bus system, c) IEEE 30-bus system, and d) NE 39-bus system.

DownLoad: Full-Size Img PowerPoint

Table 1.  Locations of ZIBs and radial buses for the systems.

Test systems	Zero injection buses		Radial buses
	No.	Locations	No.	Locations
14-bus	1	7	1	8
30-bus	7	6, 9, 22, 25, 27, 28	3	11, 13, 26
NE 39-bus	12	1, 2, 5, 6, 9, 10, 11, 13, 14, 17, 19, 22	9	30, 31, 32, 33, 34, 35, 36, 37, 38
57-bus	15	4, 7, 11, 21, 22, 24, 26, 34, 36, 37, 39, 40, 45, 46, 48	1	33
118-bus	10	5, 9, 30, 37, 38, 63, 64, 68, 71, 81	7	10, 73, 87,111,112,116,117

---

 | Show Table

DownLoad: CSV

5.2.   Case studies

The performance of FPA is tested by four test cases. These cases are conducted in details on 14-bus IEEE standard network that is shown in Figure 4(a) the explanation of these test cases are:

5.2.1.   Normal case

In this case, the objective is to achieve full system observability without considering the existence of ZIB and without losing any PMUs. By using Eq 5, the binary bus connectivity matrix is created for the IEEE 14-bus as shown in (16). The inequality constraints of the A-matrix are formulated as shown in (17).

These constraints mean that according to Eq 17e, installing PMU at bus 5, buses 1, 2, 4, 5 and 6 will be observable.

5.2.2.   Considering the existence of ZIB

Based on Figure 4a, bus 7 and bus 8 are ZIB and radial bus, respectively. According to the first rule of merging process of ZIBs, bus 8 will be merged with bus 7. This process leads to removing the constraint of bus 7 and then connect bus 8 with buses 4 and 9 directly. Then the constraints of buses 4, 8 and 9 are updated to reflect the merging process and reformulated as follows:

The merging process is shown below in Figure 5.

Figure 5.  Modeling of ZIB for IEEE 14-bus system.

DownLoad: Full-Size Img PowerPoint

5.2.3.   Failure of PMU

In order to improve the power system reliability and ensure system complete observability under failure of PMU, each bus in the power system must be observed by at least two PMUs. This is reflected in the constraints by multiplying Eq 6 right term by 2 to find Eq 19.

Then, we have

5.2.4.   Single line outage

It is a common fault in the power systems. If a bus is being observed by two PMUs, then a related line loss will not affect the complete observability of the power system. This can be achieved by constraints that are given in Eq 19. In this case, every radial bus has only one incident branch. So when losing that incident branch, that radial bus will be unobservable. Wherefore, these radial buses should be excluded from the system as well as those inequality constraints. As it is impossible to observe it through two lines.

5.3.   Simulation results

The effectiveness and performance of the proposed optimization method is assessed by applying it on the IEEE 14-bus, IEEE 30-bus, IEEE 57-bus, IEEE 18-bus and NE 39-bus test systems under the previous three case studies.

The results obtained for the normal case without considering neither ZIBs nor contingencies are shown in Table 2. As noticed from shown results, the FPA obtained many PMUs locations’ sets for the same number of PMUs. That proves the ability of the proposed FPA to give variety of solutions of minimum PMUs number.

Table 2.  Optimal solutions using FPA under normal operating condition.

Test System	Normal Case
	No. of PMUs	Locations sets	R. Index
14-bus	4	2, 6, 7, 9	19
		2, 6, 8, 9	17
30-bus	10	2, 4, 6, 9, 10, 12, 15, 18, 25, 27	52
		2, 4, 6, 9, 10, 12, 19, 24, 25, 27	51
NE 39-bus	13	2, 6, 9, 10, 13, 14, 17, 19, 20, 22, 23, 25, 29	52
		2, 6, 9, 10, 11, 14, 17, 19, 22, 23, 25, 29, 34	51
57-bus	17	1, 4, 6, 9, 15, 20, 24, 28, 31, 32, 36, 38, 41, 47, 51, 53, 57	72
		1, 4, 7, 9, 15, 20, 24, 28, 31, 32, 36, 38, 41, 46, 50, 53, 57	71
118-bus	32	1, 5, 9, 11, 12, 17, 21, 23, 28, 30, 34, 37, 42, 45, 49, 53, 56, 62, 64, 68, 71, 75, 77, 80, 85, 87, 91, 94,101,105,110,115	160
		3, 5, 10, 12, 13, 17, 21, 24, 25, 28, 34, 37, 40, 45, 49, 53, 56, 62, 63, 68, 71, 75, 77, 80, 85, 86, 91, 94,101,105,110,114	157

---

 | Show Table

DownLoad: CSV

The results obtained for the second case which includes considering ZIBs are shown in Table 3. As depicted in Table 3, it is obvious that considering ZIBs helps in decreasing the number of PMUs that is required to fulfil complete system observability. It saves PMUs and in turn saves money as the overall cost will be decreased because of decreasing PMUs number and their needed connections. For example, it saves a PMU for 14-bus network, three PMUs for 30-bus network, five PMUs for 57-bus network and NE 39-bus network.

Table 3.  Optimal PMU locations obtained by FPA with considering ZIB.

Test systems	Considering ZIB
	No. PMUs	Locations sets	R. Index
14-bus	3	2, 6, 9	15
30-bus	7	1, 7, 10, 12, 18, 24, 29	29
		3, 5, 10, 12, 18, 24, 29	29
NE 39-bus	8	3, 8, 12, 16, 20, 23, 25, 29	32
57-bus	12	1, 6, 9, 14, 19, 25, 29, 32, 38, 41, 50, 53	52
		2, 6, 12, 14, 19, 25, 29, 32, 38, 41, 51, 54	49
118-bus	29	2, 8, 11, 12, 17, 20, 23, 28, 33, 34, 40, 45, 49, 53, 56, 61, 66, 72, 75, 77, 80, 85, 86, 91, 94,102,105,110,114	143

---

 | Show Table

DownLoad: CSV

The results obtained for the third case that includes considering a loss of PMUs are shown in Table 4. It is obvious that more benefits need more cost. So, to improve the system reliability, the PMUs number should be increased which in turn increases cost. In that case, the PMUs number depends on the radial buses and the buses that have only two incident buses. The more these buses in the system, the more PMUs needed. And that is depicted in Table 4, the number of PMUs is increased by 5 for 14-bus network, 11 for 30-bus network, 16 for 57-bus network and NE 39-bus network, and finally increased by 37 for 118-bus network.

Table 4.  Optimal solutions using FPA with considering loss of PMU.

Test systems	Loss of PMU
	No. of PMUs	Locations sets	R. Index
14-bus	9	2, 4, 5, 6, 7, 8, 9, 11, 13	39
		1, 2, 4, 6, 7, 8, 9, 11, 13	37
30-bus	21	1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 17, 18, 20, 22, 24, 25, 26, 27, 28, 29	83
		2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 15, 17, 19, 20, 21, 23, 25, 26, 27, 30	82
NE 39-bus	29	2, 3, 4, 6, 8, 9, 10, 11, 12, 14, 16, 17, 19, 20, 22, 23, 25, 26, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39	99
57-bus	33	1, 3, 4, 6, 9, 11, 12, 15, 19, 20, 22, 24, 25, 27, 28, 29, 30, 32, 33, 35, 36, 38, 39, 41, 45, 46, 47, 50, 51, 53, 54, 56, 57	129
118-bus	69	1, 3, 5, 7, 9, 10, 11, 12, 15, 17, 19, 21, 22, 24, 25, 27, 29, 30, 31, 32, 34, 36, 37, 40, 42, 44, 45, 46, 49, 51, 52, 54, 56, 57, 59, 62, 64, 65, 66, 68, 70, 71, 73, 75, 76, 77, 79, 80, 82, 83, 85, 86, 87, 89, 91, 92, 94, 96,100,102,105,106,109,110,111,112,114,116,117	313

---

 | Show Table

DownLoad: CSV

The optimal number in case of considering the failure of a single line between two buses is depicted in Table 5.

Table 5.  Optimal solutions using FPA with considering a single line outage.

Test systems	Single Line Outage
	No. of PMUs	Locations sets	R. Index
IEEE 14-bus	7	2, 4, 5, 6, 9, 10, 13	33
IEEE 30-bus	16	1, 2, 4, 5, 6, 10, 12, 15, 16, 18, 19, 22, 24, 27, 28, 30	71
NE 39-bus	15	2, 3, 6, 8, 9, 11, 13, 14, 16, 17, 22, 23, 26, 29, 39	63
		1, 2, 3, 6, 8, 9, 11, 13, 14, 16, 17, 22, 23, 26, 29	63
IEEE 57-bus	32	1, 2, 4, 6, 9, 11, 12, 15, 19, 20, 22, 24, 25, 27, 28, 29, 30, 32, 34, 36, 37, 38, 39, 41, 45, 46, 47, 50, 51, 53, 54, 56	127
IEEE 118-bus	61	1, 3, 5, 7, 8, 11, 12, 15, 17, 19, 21, 22, 24, 25, 27, 29, 30, 31, 32, 34, 36, 37, 40, 42, 44, 45, 46, 49, 51, 53, 54, 56, 57, 59, 62, 64, 65, 66, 68, 70, 71, 75, 76, 77, 79, 80, 82, 83, 85, 89, 91, 92, 94, 96,100,102,105,106,109,110,114	297

---

 | Show Table

DownLoad: CSV

5.4.   Comparison with other algorithms

To prove that the suggested FPA has a higher performance in solving the OPP, it must be compared with other algorithms that have been used in solving the OPP. Comparison are conducted based on two phases; results and performance. Tables 6–9 depict the comparisons between FPA and other algorithms with respect to the best results. Table 6 depicts a comparison between FPA and other optimization algorithms for solving OPP for normal case. FPA gives the same optimal numbers of PMUs like other methods but with different locations and with greater R. index. Table 7 depicts a comparison between the suggested FPA and other optimization algorithms for solving OPP with considering ZIBs. The results of using FPA are the best in networks 14-bus, 30-bus and NE-39-bus, respectively, while FPA gives the better redundancy R. index in networks 57-bus and 118-bus. Table 8 depicts a comparison between the suggested FPA and other optimization algorithms for solving OPP for normal case with considering loss of PMU. The results of FPA are the same other methods but with greater R. index number in networks 14-bus, 30-bus and 57-bus and it has the gratest R. index in case of NE 39-bus and 118-bus. Finally, the comparison in case of considering the loss of single branch between busses is shown in Table 9 and the results of FPA are the best. From the results depicted in Tables 6-9, it is noticed that the suggested FPA is one of the best algorithms to be used in solving OPP problem as it has the ability to fulfil a complete observability of the system with lower number of needed PMUs and a variety of PMUs locations sets.

Table 6.  Comparison between algorithms for normal case.

Algorithms	IEEE 14-bus	IEEE30-bus	NE39-bus	IEEE57-bus	IEEE118-bus
Exhaustive Search Algorithm (ES) [7]	4, R19	10, R50	-	-	-
Integer Quadratic Programming (IQP) [8]	4, R19	10, R49	-	17, R69	32, R159
Binary Integer Linear Programming (BILP) [27]	4, R18	10, R49	-	17, R69	32, R158
Topology Transformation Method (TT) [28]	4, R19	10, R51	-	17, R71	32, R160
Staged ES [34]	4, R18	10, R50	13, R49	17, R70	32, R159
Taguchi binary bat algorithm (TBBA) [37]	4, R19	10, R51	-	17, R71	32, R160
Proposed FPA	4, R19	10, R52	13, R52	17, R72	32, R160

---

 | Show Table

DownLoad: CSV

Table 7.  Comparison between algorithms for considering ZIBs.

Algorithms	14-bus	30-bus	NE 39-bus	57-bus	118-bus
ES [7]	3, R15	7, R28	8, R30	-	-
Integer Linear Programming (ILP) [11]	3, R14	7, R28	8, R29	11, R50	28, R141
GA [15]	3, R15	7, R29	-	12, R52	29, R142
TT [28]	3, R15	7, R29	8, R31	11, R51	28, R143
ILP [29]	3, R14	-	-	12, R53	29, R142
Binary Particle Swarm (BPSO) [30]	3, R15	7, R29	-	13, R54	29, R143
Branch and Bound (B & B) [31]	-	7, R27	9, R33	12, R53	29, R141
Differential Evolution (DE) [32]	3, R15	7, R29	8, R31	11, R50	29, R143
Improved PSO (IPSO) [33]	-	7, R29	8, R30	11, R52	-
Staged ES [34]	3, R15	7, R29	8, R31	11, R49	28, R140
Proposed FPA	3, R15	7, R29	8, R32	12, R52	29, R143

---

 | Show Table

DownLoad: CSV

Table 8.  Comparison between algorithms for considering loss of PMU.

Algorithms	14-bus	30-bus	NE 39-bus	57-bus	118-bus
IQP[8]	9, R37	21, R80	-	33, R128	68, R310
Integer Programming (IP) [10]	9, R39	22, R88	-	35, R133	72, R318
Modified Binary PSO (MBPSO) [35]	9, R39	21, R82	28, R96	33, R129	68, R310
Binary Semi-Definite Programming (BSDP) [36]	9, R38	-	-	-	72, R318
TBBA [37]	9, R39	21, R82	-	33, R128	68, R312
Proposed FPA	9, R39	21, R83	29, R99	33, R129	69, R313

---

 | Show Table

DownLoad: CSV

Table 9.  Comparison between algorithms for considering a single line outage.

Algorithms	14-bus	30-bus	NE 39-bus	57-bus	18-bus
IQP [8]	9, R37	21, R80	-	33, R128	68, R310
ILP [38]	9, R36	21, R79	28, R97	33, R129	68, R307
MBPSO [39]	9, R39	-	-	-	72, R317
Proposed FPA	7, R33	16, R71	15, R63	32, R127	61, R297

---

 | Show Table

DownLoad: CSV

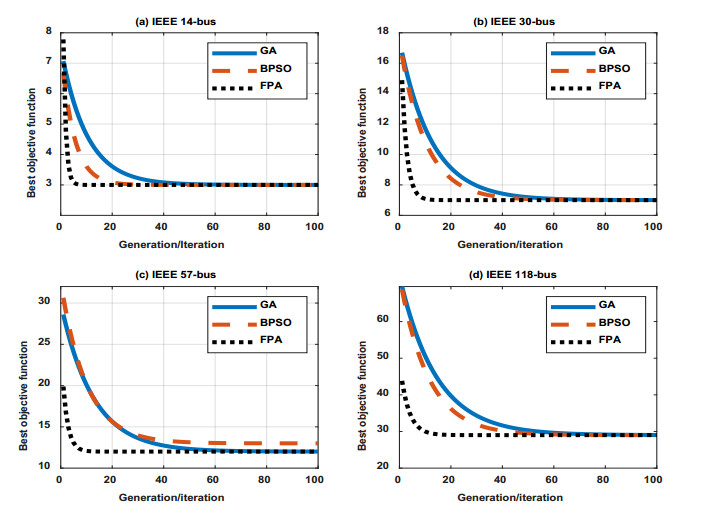
The second phase of comparison is shown in Figure 6 and Table 10. Figure 6 shows a comparison between FPA, GA ^[15] and BPSO ^[30] under normal case for the tested systems. The results show that FPA is the fastest algorithm in reaching to the optimal solution where it reaches to the optimal solution after 6, 10, 7 and 10 iterations for IEEE 14-bus, 30-bus, 57-bus and 118-bus, respectively. Also the computational time based on the used computer is compared for FPA and other method as shown in Table 10. The results show that the FPA has the minimum computational time but with high specifications computer.

Figure 6.  Comparison of FPA with GA and BPSO in terms of convergence.

DownLoad: Full-Size Img PowerPoint

Table 10.  Comparison between FPA with other methods based on computational time.

Algorithms	Computer specifications	14-bus	30-bus	57-bus	118-bus
IQP [8]	Intel Xeon 3.4-GHz CPU with 2 GB RAM	3.09	2.6	4.24	3.09
Integer Linear Programming (ILP) [11]	2.13-GHz Intel(R) Core(TM) 2 CPU with 2 GB RAM	0.05	-	30.41	1625.30
ILP [29]	Intel Core2 Duo CPU E7500 running at 2.93-GHz with 2 GB RAM	0.04	-	1.93	6.37
Differential Evolution (DE) [32]	Intel Xeon 3.4-GHz CPU with 2 GB RAM	2	4	2	3
MBPSO [39]	Centrino 1.6-GHz CPU with 512 MBRAM	0.052	0.071	0.106	0.169
Proposed FPA	Intel Core i7 2.67-GHz CPU with 6-GB RAM	0.02	0.51	0.1	0.1

---

 | Show Table

DownLoad: CSV

6.   Conclusions

The results obtained confirms that the proposed optimization method (FPA) can solve the OPP problem to fulfil the complete power system at different case studies such as normal case, then considering of ZIBs which helps in decreasing the PMUs number that is required to make the power system complete observable and contingencies such as the case of loss of PMU and the case of single line failure to improve the power system reliability and guarantee complete observability of the power during losing of PMU. FPA is also has the ability of finding variety of PMUs location sets for the same number of PMUs which help in increasing the measurement redundancy of the system. And by comparing the obtained results of the suggested FPA with results of other optimization algorithms used to solve the OPP, it is clear that the suggested FPA is considered to be one of the methods that having high performance and efficiency in solving the OPP to find the minimum PMUs number to fulfil the power system observability at different case studies and different test systems with different number of buses and with different connections.

Conflicts of interest

The authors declare no conflict of interest.