Analysis of differential code biases and inter-system biases for GPS and NavIC satellite constellations

1.   Introduction

The multi-constellation and multi-frequency GNSS systems such as GPS (United States), GLONASS (Russia), BeiDou (China), GALILEO (European), and DORIS (France) satellite navigation systems are progressively realizing global continuous navigation and positioning services. NavIC is an Indian Regional Navigation Satellite System, developed by the Indian Space Research Organization, India. NavIC consists of 4 Geo Synchronous Orbit (55⁰E and 111.75⁰E) at an inclination angle of 27⁰, 3 Geo-Stationary Satellites (32.5⁰E, 83⁰E, and 129.5⁰E) at an inclination angle of 5⁰. NavIC satellite system transmits dual-band signals in the L5 band (1176.45 MHz) and S-band (2492.28 MHz) signals. NavIC provides two categories of positioning services, namely standard positioning service (SPS) for civilian users and restricted service (RS) for authorized navigation users. NavIC system is a regional satellite navigation system that provides continuous PVT services under northern low latitude and equatorial ionospheric anomaly region. The ground-based GNSS (GPS/GLONASS/Beidou/NavIC) receivers continuously acquire GPS data for space weather, atmospheric earthquake/Tsunami, and Geodetic applications.

The estimation of TEC accuracy depends on the hardware biases of ground-based GNSS receivers and satellites. The TEC can be computed using code and carrier phase measurements. The accuracy of code and carrier phase measurements of multi-frequency GNSS measurements is limited by DCBs and ISBs, due to the delay in antenna, cables, GPS receivers, and satellite hardware. DCBs are specific to satellites and receiver hardware, whereas ISBs are performed to GPS receiver hardware due to different GNSS constellations. The variability of DCB and ISB depends on time, location, solar cycle, and geomagnetic conditions.

International GNSS Service (IGS) has developed multi-GNSS experiment analysis, monitoring, tracking, and status of the global GNSS systems ^[1,2]. The DCBs and ISBs are estimated to analyze GNSS system constellation and precise orbit positioning and precise orbit determinations in multi GNSS systems ^[3]. Arikan et al. have developed the IONOLAB BIAS method to estimate the DCBs using a single GPS station receiver ^[4]. ISB determination indicates correct orbiting errors, coordinating systems errors, clock offsets of GNSS systems ^[5]. Li et al. ^[5] have investigated ISBs due to GPS and BDS satellite navigation systems using multi-GNSS experiment observations. ISB daily and weekly characteristics are analyzed using the reverse filtering method from BDS, GPS GLONASS, and GALILEO navigation systems. Accuracy and reliability of multi-GNSS positioning, precise orbit and clock determination are estimated using GPS, GLONASS, BeiDou, and Galileo four-system observations ^[6]. Preliminary results indicate that the ISB values have correlated to receiver types and long and short-term variations of ISB ^[7]. A statistical hypothesis testing was implemented to analyze the stability of the BDS–GPS systems, and the results illustrate that ISB is receiver-dependent on different receiver types ^[8]. The principal GNSS error source is the ionospheric error, a function of TEC. The positioning accuracy has improved by incorporating ISB corrections in multi-GNSS observations models ^[9]. Researchers have investigated the relation between ISB and DCB for BDS, GPS, GLONASS, and Galileo systems, and it is found that ISBs correlated well with DCBs for different Multi GNSS receiving satellite systems for both long and short term ISB variations [3, 5‒9]. In addition to ISB corrections, Differential Code Bias (DCB) corrections are also necessary to improve the positional accuracy of multi GNSS receivers as part of deriving ionospheric differential corrections. A correlation analysis between ISB and DCBs is needed to test the stability of different types of GNSS receivers from GPS and NavIC satellite constellations ^[9]. In this paper, an attempt is made to investigate the long- and short-term variability of DCB and ISB between GPS and NavIC satellite constellations. The five ground-based GNSS multi-frequency receivers (Two GPS and three NavIC receivers) collocated at Koneru Lakshamaiah Education Foundation, Guntur, India, are considered to determine short- and long-term time series of DCB and ISB values.

2.   NavIC DCB estimation

The NavIC measurements equations for code observations are represented as follows

where, the superscript s, subscript r assign to satellite and receiver, jointly; $P_{L5}^{nav, s}$ and $P_S^{nav, s}$ perform the code phase observations at a frequency L5 and S, jointly; $t_r^s$ means the tropospheric delay; $i_{r, L5}^s$ and $i_{r, {\rm{S}}}^s$ are the ionospheric delay; $\rho _r^s$ is the geometric distance; $\mathrm{d} \mathrm{t}{_r}$ and $\mathrm{d} \mathrm{t}{^s}$ refer to the clock offsets of receivers satellites jointly; $b_{r, L5}^{nav}$ and $b_{L5}^{nav, s}$ stand for the differential biases developed with satellite receiver code measurements. The geometry-free code measurements are obtained by differencing the carrier phase and pseudo-range observations between dual-band signals, which can be denoted as ^[9]

Here the superscript s, subscript r assign to satellite and receiver, jointly; $L_{L5}^{nav, s}$ and $L_s^{nav, s}$ perform the carrier phase observations at frequency L5 and S, jointly; dual-frequency measurements are used to estimate the NavIC DCBs ^[14].

Where, j indicate to the carrier frequency; ${{\rm{d}}_{r, j}}$ and ${\rm{d}}_j^s$ are the pseudo-range code biases of ground-based receiver and space satellite, although ${b_{r, j}}$ and $b_r^s$ are indicate the ground-based receiver and space satellite-dependent uncelebrated phase delay; ${\lambda _j}$ means the wavelength; $N_{r, j}^s$ means the ambiguity factor; $i_{r, j}^s$ & $t_r^s$ means the ionospheric & tropospheric delay, jointly; $e_{r, j}^s$ and $\varepsilon _{r, j}^s$ indicate to the noises and multipath errors.

When smoothed geometry-free pseudo range observations shown in Eq (3)

Here $P_{4, n}^{nav.s}$, $L_{4, n}^{nav, s}$ are the geometry-free linear combination of pseudo-range measurements and geometry-free linear combination of carrier phase measurements at the n^th epoch and N is the number of observations.$k$ is the epoch after applying the technique of carrier levelling of code phases.

The difference between pseudo-range measurements at frequency L5 and S, jointly determines the geometry-free linear combination of pseudo-range represented as $P_{4, n}^{nav.s}$.

Similarly, the difference between carrier phase measurements at frequency L5 and S, is jointly determine the geometry-free linear combination of carrier phase represented as $L_{4, n}^{nav, s}$.

The combined satellite and receiver DCBs can be denoted as

Here ${\rm{A}} = 40.3 \times {10^{16}} \times (\frac{1}{{{f^2}_{L5}}}{\rm{ - }}\frac{1}{{{f^2}_{{S^{}}}}}),$ here $c$ is velocity of light equal to 3×10⁸ m/s².

Where ${f^{}}_{L5}$ and ${f_{{S^{}}}}$ are the frequencies of carrier phases for L5 and S, bands signals jointly; $DCB_r^{nav}$ = ${\rm{b}}_{r, L5}^{nav} - {\rm{b}}_{r, S}^{nav}$ and $DC{B^{nav,{\rm{s}}}} = b_{L5}^{nav,{\rm{s}}} - b_S^{nav,{\rm{s}}}$ are the ground-based receiver (RDCBs) and SDCBs, accordingly. The DCBs are the zero-mean condition for all satellites and can be denoted as ^[10].

NavIC TEC was estimated using local GPS TEC observations with planar fit ionospheric model.

The NavIC TEC values can be estimated as

Here (x1, y1) is the local coordinate values of NavIC ionospheric pierce point (IPP) and (a0, a1, a2) are the planar coefficient estimated from the local GPS TEC observations ^[14]

The difference between DCB of NavIC can be estimated as ^[11]

The difference between DCB of GPS can be determined as

where $DCB_r^{nav}$ and $DCB_r^{gps}$ represent the differences RDCBs between the station and reference stations for GPS and NavIC, respectively; The receiver DCB differences between GPS and NavIC. After eliminating reference DCB can be expressed as follows ^[9],

The DCB difference between NavIC and GPS is analyzed by the double DCB differences of a reference receiver station.

3.   Determination of ISB between NavIC and GPS satellite constellations

The time delay between the two different band signals in one receiver system, in which the band of signals is in the same constellation or different constellation of a GNSS system, is inter-system bias (ISB). The Parameter can be estimated from the pseudo-range and carrier phase observations from the two satellite constellations, and depends on the satellite, receiver clocks offsets ^[5]. Accords GNSS receiver collects GPS and NavIC data on L1, L5, and S-band signals A287, A288, and A076. International GNSS Service (IGS) receiver provides ISB observables between GPS and NavIC system. IRNSS-GPS-SBAS, space-based augmentation System, International GNSS Service (IGS) Accord software & systems Pvt. Ltd India receivers can track NavIC dual-frequency (L5 band S-band), GPS (L1 band), and SBAS signals. IRNSS Data Analysis Software (IRDAS) was used to generate the ISBs by using the data provided by IGS receivers.

The ionosphere-free combination measurements are representing in the below expression,

Here superscript "N" & "G" indicate the NavIC and GPS satellites, jointly; $\alpha$ means the unit vector of the direction from ground-based receiver to satellite, ${R_r}$ means to the increment vector of the ground-based receiver position; $\varphi \left({t, {t_0}} \right)$) means the state transition matrix from initial epoch time"t0" to epoch time t; ${M_{r, trop}}$ indicates the wet mapping function; and $ZT{D_r}$ means to the remaining part of the zenith wet tropospheric delay. "$O_O^{}$" is the initial satellite orbit state vector; x0, y0, z0 are the initial positions of the satellite; even x0', y0', z0' is the velocity; $SPR_1^G$, $SPR_2^G$, …$SPR_n^G$ indicates to solar radiation pressure measurements. In a ground-based receiver, the code delays of NavIC (${d_{r, N, IF}}$) & GPS (${d_{r, G, IF}}$) are different, and this type of difference is a kind of inter-system biases (ISBs). Eq (12) can be expressed as:

The initial NavIC and GPS satellite orbit state vector can be rewritten as:

where $d{t_{r,{\rm{G}}}} = d{t_r} + c \times {d_{r,{\rm{G}},{\rm{IF}}}}$ is the clock bias of GPS; $IS{B_{r,{\rm{G}} - N,IF}} = {b_{r,N,IF}} - {b_{r,{\rm{G}},IF}}$ is code ISB measurements for NavIC relative to GPS. In this study, we denoted the GPS + NavIC precise orbit determination. The clocks bias of NavIC are obtained as follows:

where, $d{t_{r, {\rm{N}}2}}$ reference to the receiver clock biases for NavIC, respectively; $d{t_{r, {\rm{G}}}}$ are the clock biases for GPS obtained from GPS + NavIC precise orbit determination, respectively, $IS{B_ {r, G - N2 }}$ is the code ISBs of NavIC and GPS satellites.

4.   Results and discussion

Three NavIC receivers (Accord software & systems Pvt. Ltd, India) Model No: A076, A287, A288, and two dual-frequency GPS receivers (GPStation 6, NovAtel, Canada) collocated at Koneru Lakshamaiah Education Foundation, Guntur, India. NavIC (L5 and S signals) and GPS (L1 and L2) data were recorded from January to April 2019 and analyzed to investigate the long-term relationship between DCBs and ISB. The code and carrier phase measurements are obtained using five GNSS receivers for all NavIC and GPS satellites. The pre-processing steps, such as outlier detection, cycle slip detection, and smoothing algorithm, are performed ^[13]. Different GNSS receiver types calculate the DCBs and double differences DCBs Code and carrier phase measurements.

4.1.   GPS satellites DCB analysis

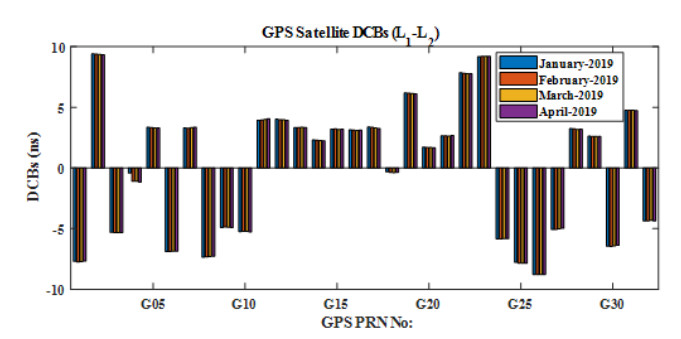
Figure 1 shows GPS satellite DCBs acquired by the Center for Orbit Determination in Europe (CODE) website (ftp://ftp.aiub.unibe.ch/CODE/). The monthly P1-P2 code measurements of GPS satellites' DCB are considered to check the DCB variability for 4 months (January-April 2019). GPS satellites PRN No 2,and No.23 satellites are experienced the maximum DCB value of about 9.3 ns. The minimum and maximum standard deviations for GPS satellites SDCBs are 0.077 ns for G26 and 0.346 ns for G04 satellites. It is noted that all GPS satellite DCBs are stable for the during from January to April 2019. In addition,the NovAtel GPS receivers (GPstation 6) inbuilt self-calibration instrumental bias algorithm was considered to determine GPS receiver DCBs at Koneru Lakshamaiah Education Foundation,Guntur,India,^[12]. As a result, the GPS receiver DCBs were estimated as 3.05 ns and 1.29 ns for GPS Rx1 and GPS Rx2 receivers.

4.2.   DCB estimation for NavIC satellites

The following steps are implemented in the estimation of NavIC DCBs.

Step 1: The pseudo carrier and code phase measurements (L5 and S) of NavIC observations are considered.

Step 2: Planar fit coefficients are estimated from the local GPS TEC observations using the modified planar fit ionospheric model. These coefficients are used to estimate the VTEC values at the corresponding IPP trajectories of NAVIC satellites.

Step 3: The geometric free code observations, geometric carrier phase observations are calculated using Eq (1) and Eq (2), and Plasmasphere Electron Content (ECpl), is obtained from IRI- Plas 2017 models and substracted for NAVIC TEC estimations.

Step 4: Smoothed geometric free code and carrier phase observations are computed.

Step 5: Satellite and receiver DCBs are seperated by zero-mean conditions from all combined NAVIC DCBs.

GPS-aided with the NavIC DCB algorithm is used to estimate the NavIC satellites and receiver DCBs, as shown in Figure 2. The NavIC PRN 3 satellite has observed a maximum DCB value of 6.3 ns. Standard deviation values are below 0.40 ns, indicating NavIC GSO satellites' high stability (Table 1). On the other hand, the standard deviation values NavIC GEO satellites PRN 7 is 0.84 ns indicating low stability. GSO Satellites have fewer standard deviations than GEO satellites due to lower elevation angles and multipath effects on GNSS signals ^[16]. Megha at al. also reported that NavIC GEO's DCB are noisier than GSO's ^[15].

Figure 3 shows long-term DCBs values determined using five GNSS receivers' data (January to April 2019) at Koneru Lakshamaiah Education Foundation, India. The maximum DCBs are 29.23 ns, 16.36 ns, and 19.25 ns are attained by NavIC A076, A287, A288 receivers, respectively, as indicated in blue, brown, gold color lines and GPS1, GPS2 maximum DCBs are 3.90 ns, 1.48 ns respectively as indicated in violet and green color line. NavIC A076 receiver DCB has estimated as 29 ns.

Figure 4 shows the difference in DCB between NavIC and GPS receivers combinations. The observation data are processed to analyze the difference DCBs for DOY 1-120, 2019. In the first combination, the DCBs difference between NavIC receiver A076 and A287 the maximum, minimum, mean values are 16.87 ns, 8.01 ns, 12.28 ns, respectively, as indicated in the brown color line. The maximum, minimum, mean values in the second combination are 13.38 ns, 4.10 ns, and 8.38 ns, respectively, as indicated in the gold color line. In the third combination, the DCB difference between NavIC Receiver A288 and A287. As indicated in the violet color line, the maximum, minimum, mean values are 7 ns, –0.40 ns, and 3.89 ns, respectively. Finally, in the fourth combination, the DCB difference between GPS Receiver GPS1 and GPS2, the maximum, minimum, mean values are 2.62 ns, 0.61 ns, 1.75 ns, respectively, as indicated in the blue color line.

Figure 5 shows double-difference DCB results between NavIC receivers concerning GPS receiver. In the first combination, the Double Difference DCBs between NavIC Receiver A076 and A287, the maximum, minimum, mean values are 15.11 ns, 6.36 ns, 10.52 ns, respectively, as indicated in the blue color line. In the second combination, the Double Difference DCB between NavIC Receiver A076 and A288. As indicated in the brown color line, the maximum, minimum, mean values are 11.61 ns, 2.36 ns, and 6.62 ns, respectively. Finally, in the third combination, the Double Difference DCB difference between NavIC Receiver A288 and A287. The maximum, minimum, mean values are 5.02 ns, ‒1.85 ns, and 2.13 ns, respectively, as indicated in the gold color line, considering that DCB between GPS1 and GPS2 is the reference point. From Figure 5 it is, evident that larger DCB values were obtained for A076-A287 GNSS receivers. Therefore, the first DCB difference between A076 and A287 is more significant than the other two combinations. The stability analysis of DCBs is estimated using zero-mean conditions. The daily variability DCBs are verified with a difference and double difference of GPS and NavIC constellations. The ambiguity issue can be resolved by taking a double difference of the GNSS observations. Zhang et al. have also analyzed DCB variability in single and double differences of DCB estimations ^[11].

4.3.   Analysis of inter-system bias (ISB)

The ISB Difference between NavIC and GPS systems for three Accords GNSS receivers is shown in Figure 6. It is found that there is a systematic bias between NavIC and GPS is observed in both DCBs and code ISBs.

Figure 6 shows the Short Term Inter system bias (ISB) values for 6 days from DOY 1 to 6, 2019. It can be seen that ISB is different for different NavIC Receivers. The maximum, minimum, and mean ISB values of the NavIC A076 receiver are 44.76 ns, 11.86 ns, and 28.83 ns, respectively, as indicated blue color line. The ISB maximum, minimum, and mean values of NavIC A287 receiver are 11.44 ns, ‒1.24 ns, and 5.47 ns, respectively, as indicated in the gold color line. The ISB maximum, minimum, and mean values of NavIC A288 receiver are 9.61 ns, ‒2.60 ns, 4.88 ns, respectively, as indicated brown color line.

Figure 7 shows the time series of three NavIC receiver ISB values from DOY 1 to 30, 2019. Intersystem bias (ISB) mean values are about 30.86 ns, 7.17 ns, 6.57 ns for NavIC (A076, A287, A288) receivers. Intersystem bias (ISB) maximum values are about 44.76 ns, 11.86 ns for A076, receiver and 11.44 ns, ‒1.24 ns for A287, receiver and 9.61 ns, ‒2.60 ns for, A076 and A288 receivers, respectively. The ISB is receiver-dependent, and different receiver types have different ISBs. The difference in ISB and DCB occurs may be due to pseudo-range observations and the time offsets. A systematic difference is identified for NavIC receivers between DCBs and ISBs (Figs 5‒7). The DCBs and ISB results reveal that GPS and NavIC satellites are stable.

5.   Conclusions

This paper estimates and analyzes the DCBs and ISBs of NavIC and GPS systems using five co-located GNSS receivers at low latitude, Guntur, India. Determination of ISB is necessary for coordinate systems, clock products, precise orbit, and precise point positioning applications. Short and long-term ISBs variations are analyzed. A systematic error is noticed from the DCB and ISB temporal variations from January to April 2019. The NavIC GSO satellites are more stable as compared to GEO satellites due to low elevation angle and multipath effects. The GPS satellites are stable compared to NavIC GEO and GSO satellites in terms of DCB and ISB analysis. The modeling of ISB stability with more different types of GNSS receivers will be explored shortly.

Acknowledgements

The present work was supported by the IRNSS Navigation receiver Field Trail and data collection MoU between SAC/ISRO and KLEF (KL Deemed to University).

Conflict of interest

The authors declare that there is no conflict of interest.