Pattern analysis of continuous analytic wavelet transforms of the COVID19 spreading and death

Yanshuo Wang; Yanshuo Wang

doi:10.3934/bdia.2020003

Big Data and Information Analytics

2020, Volume 5, Issue 1: 29-46. doi: 10.3934/bdia.2020003

Previous Article Next Article

Research article

Pattern analysis of continuous analytic wavelet transforms of the COVID19 spreading and death

Yanshuo Wang ^,

Data Mining and Reliability Consultant, LLLW LLC Inc., Lansing, MI, USA

Received: 15 August 2020 Accepted: 24 September 2020 Published: 09 October 2020

This paper is to use the wavelet transform method with Morse wavelet to analyze the daily confirmed cases and deaths of COVID19 in China, U.S.A, Spain, Italy, France, Germany, U.K., South Korea, Michigan and New York City. Wavelet transform is frequently used for time series data to extract the frequency localization information in last two decades. The wavelet transform with Morse wavelet is applied to the daily infected cases and deaths of COVID19 at different countries/places. There are multiple scales (frequencies) of COVID19 spreading with different magnitude at the specific time which can be identified in Wavelet magnitude scalogram plots. For example, in China, the highest magnitude (2000 to 2500) spreading happened on 2/12/2020 with scale around 329 to 434, but in U.S.A the highest magnitude (4000 to 4500) spreading happened during 4/25/2020 and 4/28/2020 with scale 137 to 183. The summary of the wavelet magnitude and scale at specific period for different countries/places is presented in this paper.

Keywords:

Citation: Yanshuo Wang. Pattern analysis of continuous analytic wavelet transforms of the COVID19 spreading and death[J]. Big Data and Information Analytics, 2020, 5(1): 29-46. doi: 10.3934/bdia.2020003

Related Papers:

[1]	Shuqi Wang, Wen Tang, Liyan Xiong, Mengyu Fang, Bingsong Zhang, Chi-Yang Chiu, Ruzong Fan . Mathematical modeling of transmission dynamics of COVID-19. Big Data and Information Analytics, 2021, 6(0): 12-25. doi: 10.3934/bdia.2021002
[2]	Ugo Avila-Ponce de León, Ángel G. C. Pérez, Eric Avila-Vales . A data driven analysis and forecast of an SEIARD epidemic model for COVID-19 in Mexico. Big Data and Information Analytics, 2020, 5(1): 14-28. doi: 10.3934/bdia.2020002
[3]	Antonio N. Bojanic . Accounting for the Trump factor in modeling the COVID-19 epidemic: the case of Louisiana. Big Data and Information Analytics, 2021, 6(0): 74-85. doi: 10.3934/bdia.2021006
[4]	Jiaqi Ma, Hui Chang, Xiaoqing Zhong, Yueli Chen . Risk stratiﬁcation of sepsis death based on machine learning algorithm. Big Data and Information Analytics, 2024, 8(0): 26-42. doi: 10.3934/bdia.2024002
[5]	Guojun Gan, Kun Chen . A Soft Subspace Clustering Algorithm with Log-Transformed Distances. Big Data and Information Analytics, 2016, 1(1): 93-109. doi: 10.3934/bdia.2016.1.93
[6]	Cun Chen, Hui Peng . Dynamic mode decomposition for blindly separating mixed signals and decrypting encrypted images. Big Data and Information Analytics, 2024, 8(0): 1-25. doi: 10.3934/bdia.2024001
[7]	Bill Huajian Yang, Jenny Yang, Haoji Yang . Modeling portfolio loss by interval distributions. Big Data and Information Analytics, 2020, 5(1): 1-13. doi: 10.3934/bdia.2020001
[8]	Antonio N. Bojanic, Alejandro Jordán . Modeling the COVID-19 epidemic in Bolivia. Big Data and Information Analytics, 2020, 5(1): 47-57. doi: 10.3934/bdia.2020004
[9]	Nick Cercone . What's the Big Deal About Big Data?. Big Data and Information Analytics, 2016, 1(1): 31-79. doi: 10.3934/bdia.2016.1.31
[10]	Nickson Golooba, Woldegebriel Assefa Woldegerima, Huaiping Zhu . Deep neural networks with application in predicting the spread of avian influenza through disease-informed neural networks. Big Data and Information Analytics, 2025, 9(0): 1-28. doi: 10.3934/bdia.2025001

Abstract

1. Introduction

It was announced by the WHO that COVID19 was first localized in Wuhan, Hubei Province, China in December, 2019, and it has been a significant threat to the public health around the globe. As of May 6, 2020, globally there have been about 3.854 million confirmed cases, and about 266,000 reported deaths ^[1]. In U.S.A., there are about 1,266,442 confirm cases, and about 74,948 reported deaths ^[1]. In the state of Michigan, there are about 45,054 confirmed cases and about 4250 reported death at the time author writing this paper ^[1,2]. The COVID19 is affecting 210 countries and territories around the world and 2 international conveyances. The COVID19 is spreading into all the 50 states, District of Columbia and its territories in the United States. Because of the contagious of this disease, most of the states such as Michigan have issued the staying home order to reduce the infectious speed.

The wavelet transform is frequently used for time series data to extract the frequency localization information in last two decades. It is also used to extract information from epidemiological time series. Numerous studies in epidemiology consist of analyzing time series to extract information and to identify scales of different patterns ^[3,4]. The wavelet transform is well adapted to studying non-stationary signals, so we can develop the wavelet transform to extract the information on the COVID19 spreading/death time series data. Wavelet analysis provides both scale and time information of the analyzed signal and allows an objective separation of different structures over different scales at different times. The novel pandemic COVID19 needs more study for researchers to understand its traveling waves and spatial hierarchies. The purpose of this paper is to understand the spreading characteristics of COVID19 from a spectrum point of view.

The spreading pattern of COVID19 is different from different countries/places. Both government executive orders and culture behavior are playing an important role to slow down the spreading of the disease. The wavelet spectrum will give us a fresh view of COVID19 spreading wave and pattern in different places.

2. Materials and methods

2.1. Continuous wavelet transform

The wavelet transform of a function f(t) with finite energy is defined as the integral transform with a family of functions

${\psi ^*}_{s,t}\text{(}{u}\text{)} = \frac{1}{\sqrt{s}}\psi \text{*}\left(\frac{u-t}{s}\right)$

(1)

It is

$Wf\left(s, t\right) = \lt f\left(u\right), \psi _{s, t} \gt = {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f\left(u\right){\psi ^*}_{s,t}\left(u\right)du = {\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f\left(u\right)\frac{1}{\sqrt{s}}\psi \text{*}\left(\frac{u-t}{s}\right)du,$

(2)

where s is a scale parameter, t is a location parameter and the function ${\psi ^*}_{\text{s, t}}\text{(}{u}\text{)} = \frac{1}{\sqrt{s}}\psi \text{*}\left(\frac{u-t}{s}\right)$ are called wavelet. $\psi \text{*}\left(\frac{u-t}{s}\right)$ is called the "mother wavelet". The parameters s(s≠0) and t are used to adjust the shape and location of the wavelets respectively.

2.2. The morse wavelets

The generalized Morse wavelets are a family of exactly analytic wavelets. They are useful for analyzing modulated signals, which are signals with time-varying amplitude and frequency ^[5]. They are also useful for analyzing localized discontinuities, and isolating and extracting quantified features in time-frequency domain. Morse wavelets are defined in the frequency domain as

$\psi _{\text{P, ϒ}}\left( {\rm{ \mathsf{ ω} }} \right) = U\left(\omega \right){a}_{P, \mathrm{\Upsilon }}{\omega }^{\frac{{P}^{2}}{\mathrm{\Upsilon }}}{e}^{-{\omega }^{\mathrm{\Upsilon }}},$

(3)

where $U\left(\omega \right)$ is the unit step, ${a}_{P, \mathrm{\Upsilon }}$ is a normalizing constant, ${P}^{2}$ is the time-bandwidth product, and ${\rm{ \mathsf{ γ} }}$ > 0 is the shape parameter and characterizes the symmetry of the Morse wavelet. Much of the literature about Morse wavelets uses the oscillation control parameter β > 0, which can be viewed as a decay or compactness parameter, rather than the time-bandwidth product, ${P}^{2}$ = β ${\rm{ \mathsf{ γ} }}$ . The equation for the Morse wavelet in the Fourier domain parameterized by β and ${\rm{ \mathsf{ γ} }}$ is as following:

${\psi _{{\rm{ \mathsf{ β} }},{\rm{ \mathsf{ γ} }}}}\left( {\rm{ \mathsf{ ω} }} \right) = {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\psi _{{\rm{ \mathsf{ β} }},{\rm{ \mathsf{ γ} }}}}\text{(t)}{e}^{-\mathit{iwt}}dt = U\left(\omega \right){a}_{\beta , \mathrm{\Upsilon }}{\rm{ \mathsf{ ω} }}^{{\rm{ \mathsf{ β} }}}{e}^{-{\omega }^{\mathrm{\Upsilon }}}\text{}\text{.}$

(4)

Where

${a}_{\beta , \mathrm{\Upsilon }}\text{≜}\text{2}{\left(\frac{e\mathrm{\Upsilon }}{\beta }\right)}^{\frac{\beta }{\mathrm{\Upsilon }}}$

(5)

is a normalization constant ensuring a peak frequency of 2 ^{[6,7,8,9,10,11,12]}.

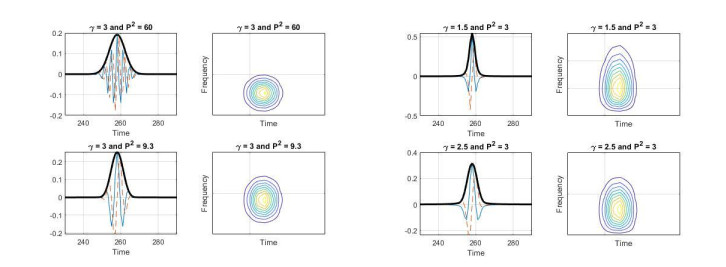
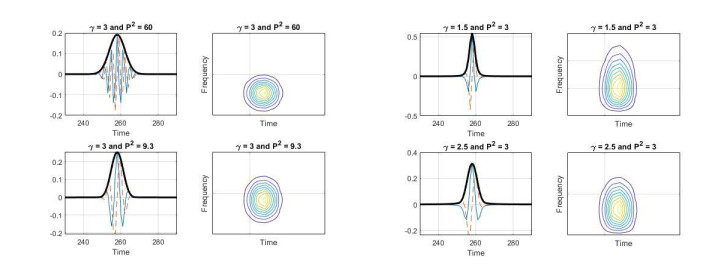
The effect of parameter ${\rm{ \mathsf{ γ} }}$ and ${P}^{2}$ values on Morse Wavelet shape are shown in Figure 1. This figure is borrowed from Matlab Morse Wavelet Tutorial ^[5].

Figure 1. The effect of parameter values of

${\rm{ \mathsf{ γ} }}$ and

${P}^{2}$ on the Morse Wavelet shape. This figure is produced using Matlab.

DownLoad: Full-Size Img PowerPoint

2.3. Application of wavelet transform

Wavelet variance (also called wavelet spectrum): Wavelet variances are computed by integrating fluctuations of wavelet functions over time for every given time scale. The values of the wavelet variance indicate the relative intensities of spreading structures at different scales ^[13,14,15]. Thus the wavelet variance may be useful for providing information about the time-scales of COVID19 spreading processes. Given the interpretation of the wavelet variance in terms of COVID19 spreading energy distribution, the scales corresponding to special peaks must contribute most to spreading energy.

Wavelet decomposition: The Mallat's multiresolution algorithm ^[16] can be used to retrieve the original from the whole set of wavelet coefficients. This "reconstruction" enables one to filter the original function, by splitting the integration domain into specific ranges of scales. Wavelet filtering can be used to isolate the two phenomena in COVID19 spreading data, if they have different scales. The wavelet decomposition is not in the scope of this paper, but it can be done in future study of COVID19.

Jump detection: "Jump" means a sharp increase or decrease in a signal. Wavelet is a localized transform, so it is useful for jump detection ^[13,14,15]. COVID19 may be associated with sudden changes or apparent discontinuities in data time series. The wavelet transform can provide information about these sudden changes and apparent discontinuities on different scales.

Time-frequency representation: Wavelets have been considered from both time and frequency points of view. For scientific applications, the localization in time and frequency domains is a key property in signal analysis ^[13,14,15]. From the time-frequency plot for COVID19 spreading, the COVID19 spreading can be recognized at different scales with the passage of time. Time-frequency representation demonstrates the usefulness of wavelet analysis in decomposing spreading waves at different scales hidden in time series data. Using two-dimensional unfolding in both time and scale, the techniques provides the location and localized spectrum for COVID19 spreading of interest. This method is especially useful for studying short lived transient events of COVID19.

3. Results

3.1. In China

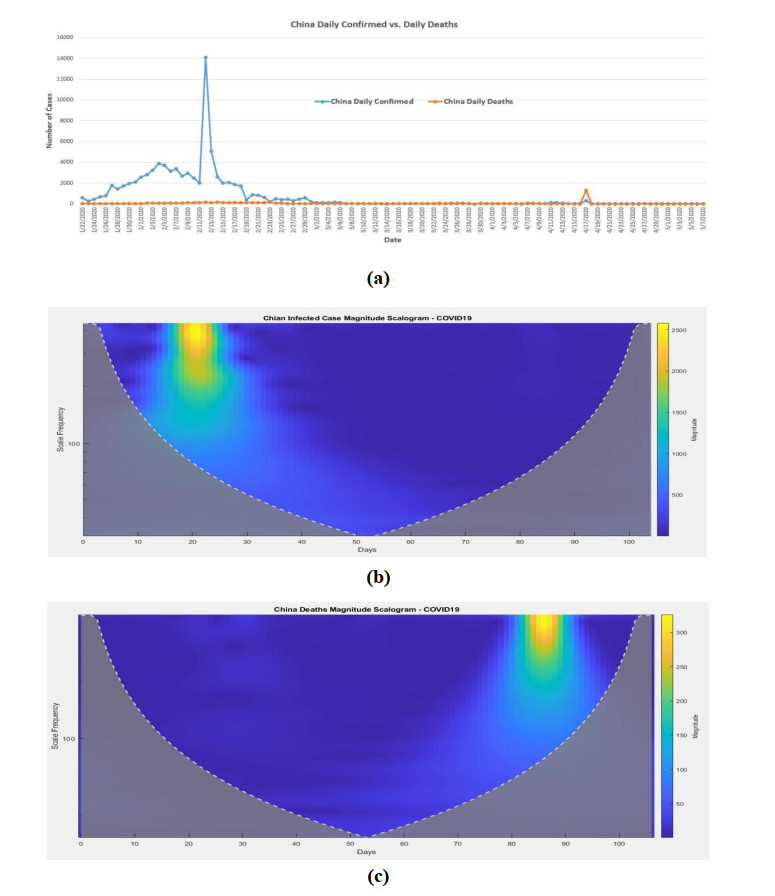
Figure 2a shows the daily infected cases and deaths in China. From 1/23/2020 (day 2) to 2/4/2020 (day 14), the trend of the daily infected cases in China was increasing, although there was small peak on 1/27/2020 (day 6). From 2/4/2020 (day 14) to 2/11/2020 (day 21), the infectious trend was decreasing. There was a big jump on 2/12/2020 (day 22), the infected cases were up to 14,108. After this huge jump, the trend of the daily infected cases was going down until 2/19/2020 (day 29). Then the trend of the daily infected cases was up and down until it was almost diminished. The Morse wavelet transform was applied to China daily infected cases and deaths. The magnitude scalogram is shown in Figure 2b, c. The horizontal axis is represented the days when COVID19 spreading. The vertical axis is represented the scale or frequency of the infection or death. The color represents the magnitude or energy of the infection or death. From Figure 2b, we notice that there was a strong magnitude of the infection around day 22 (2/12/2020), and the scale was about from 329 to 434 for high magnitude (about 2000 to 2500) infection, in the meantime, the scale was from 183 to 329 and the magnitude was about 1500 to 2000 spreading as well. The wavelet scalogram shows the different magnitudes of COVID19 spreading with different scales at the specific time period. Overall, the COVID19 spreading in China was shown to have achieved the highest speak at the maximum 434 scale around day 22 (2/12/2020), the spreading energy was decreasing after about day 50 (3/11/2020). Between day 30 (2/20/2020) and day 50 (3/11/2020), the magnitude (around 1000) was more concentrating on the scale from 206 to 30. After day 50 (3/11/2020) the spreading magnitude (dark blue color in plot) was decreasing. This can correlate the government isolation policy in China. It suggests that we can describe the COVID19 spreading trend at specific days on different spreading frequencies/scales with different spreading magnitudes/energies from the wavelet analysis.

Figure 2. (a): COVID19—China daily infected cases and deaths, the date is from 1/22/2020 to 5/7/2020. (b): COVID19—China daily infected cases wavelet magnitude scalogram, the date is from 1/22/2020 to 5/7/2020. (c): COVID19—China daily deaths wavelet magnitude scalogram, the date is from 1/22/2020 to 5/7/2020.

DownLoad: Full-Size Img PowerPoint

But looking at the magnitude scalogram of death in China from Figure 2c, the death peak (the magnitude about 320) was around day 87 (4/17/2020) at the scale from 329 to 434. Between day 83 (4/13/2020) and day 90 (4/20/2020), the medium magnitude was from 200 to 250 with the scale from 206 to 329. The wavelet provides an excellent tool to extract the COVID 19 spreading and deaths magnitude and scale patterns during different periods. This may help us to understand the spreading and death nature of COVID19 and the effectiveness of the government policy.

3.2. In U.S.A.

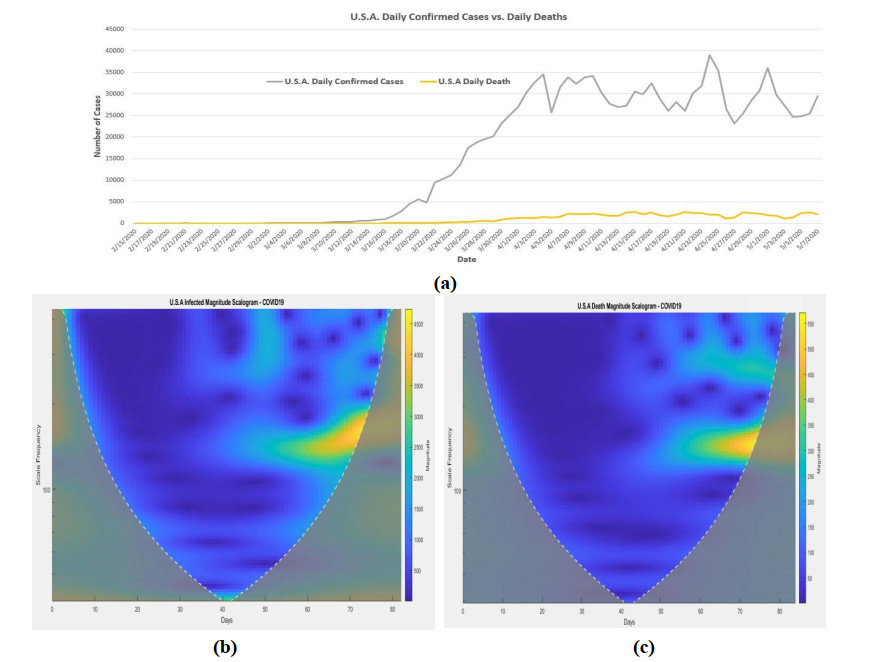
The Morse wavelet analysis is also applied to U.S.A daily infected cases and deaths. The results are shown in Figure 3b, c. From U.S.A spreading magnitude scalogram plot, the highest peak (magnitude about 4000 to 4500) was happened around the scale from 137 to 183 from the day 71 (4/25/2020) to day 74 (4/28/2020). It seems after day 40 (3/25/2020), the scale around 149 was the major threat which had the medium magnitude and it changed to highest magnitude on day 71 (4/25/2020), and also the scale around 329 with magnitude about 3000 was also the threat at day 78 (5/2/2020).

Figure 3. (a): COVID19—U.S.A daily infected cases and deaths, the date is from 2/15/2020 to 5/7/2020. (b): COVID19—U.S.A daily infected cases wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020. (c): COVID19—USA daily deaths wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020.

DownLoad: Full-Size Img PowerPoint

From the death magnitude scalogram (Figure 3c), the highest magnitude (500 to 550) of death was happened around the scale 137 to 164 from day 73 (4/27/2020) to day 75 (4/29/2020). After day 50 (4/4/2020) the scale around 150 was the major threat, and the scale around 274 at day 78 (5/2/2020) with magnitude (350 to 400) was also the threat.

3.3. In Spain

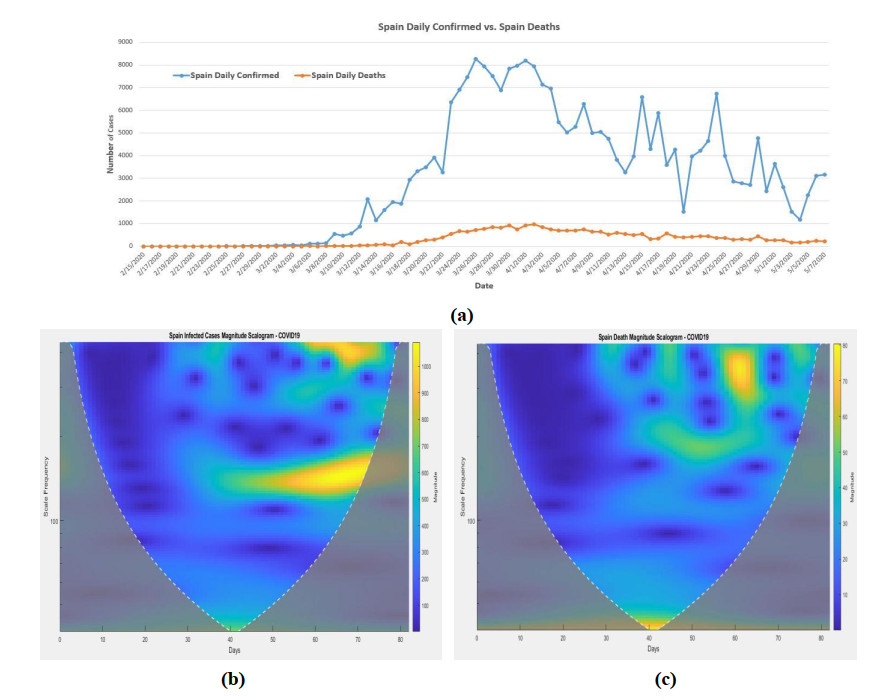
The Morse wavelet analysis is also applied to Spain daily infected cases and deaths. They are shown in Figure 4b, c. The highest spreading peak (magnitude about 900 to 1070) was happened around the scale from 137 to 164 from day 53 (4/7/2020) to day 73 (4/27/2020). There was another peak around scale 412 with magnitude about 900 to 1070 at day 60 (4/14/2020) to day 70 (4/24/2020). The medium spreading magnitude (around 600 to 700) was happened from day 35 (3/20/2020) to day 77 (5/1/2020) with different scales.

Figure 4. (a): COVID19—Spain daily infected cases and deaths, the date is from 2/15/2020 to 5/7/2020. (b): COVID19—Spain daily infected cases wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020. (c): COVID19—Spain daily deaths wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020.

DownLoad: Full-Size Img PowerPoint

From the death magnitude scalogram (Figure 4c), the highest magnitude (70 to 80) of death was happened around the scale 274 to 411 on day 57 (4/11/2020) to day 65 (4/19/2020). Around day 40 (3/25/2020), the scale around 42 also had the high magnitude (70 to 80). After day 30 (3/15/2020), the medium magnitude around 50 was also the threat with different scale.

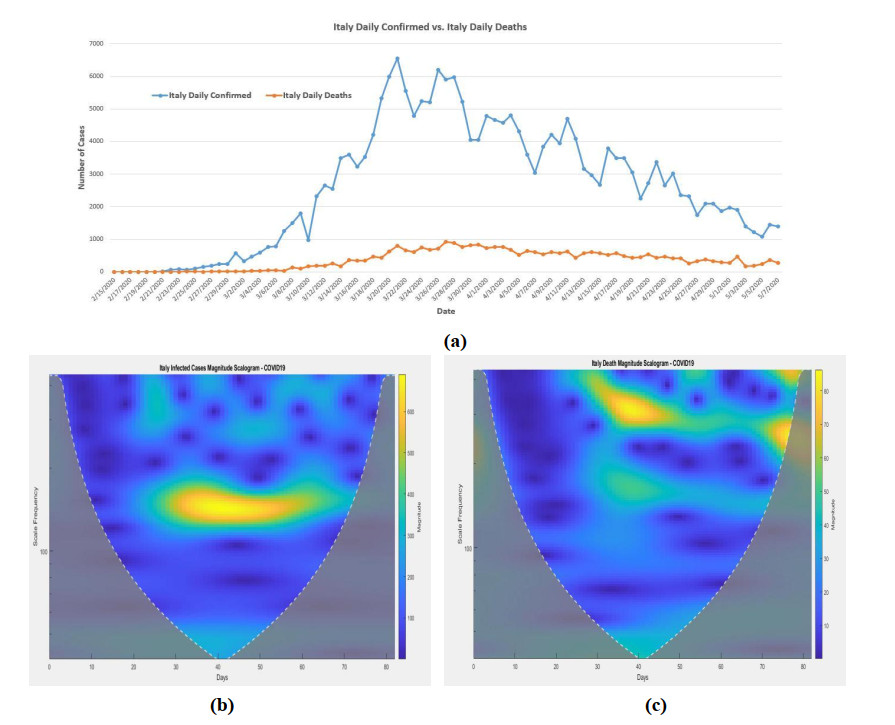
3.4. In Italy

The Morse wavelet analysis is also applied to Italy daily infected cases and deaths. They are shown in Figure 5b, c. The highest spreading peak (magnitude about 600 to 700) was happened around the scale from 126 to 164 from day 32 (3/17/2020) to day 55 (4/9/2020). The medium spreading magnitude (around 400) was happened from day 27 (3/12/2020) to day 72 (4/26/2020) with different scales.

Figure 5. (a): COVID19—Italy daily infected cases and deaths, the date is from 2/15/2020 to 5/7/2020. (b): COVID19—Italy daily infected cases wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020. (c): COVID19—Italy daily deaths wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020.

DownLoad: Full-Size Img PowerPoint

From the death magnitude scalogram (Figure 5c), the highest magnitude (75 to 85) of death was happened around the scale 274 to 329 from day 35 (3/20/2020) to day 45 (3/30/2020). Around day 72 (4/26/2020) to day 77(5/1/2020), the scale 235 to 274 also had the highest magnitude (75 to 85). After day 30 (3/15/2020), the medium magnitude from 60 to 70 was the threat with different scale.

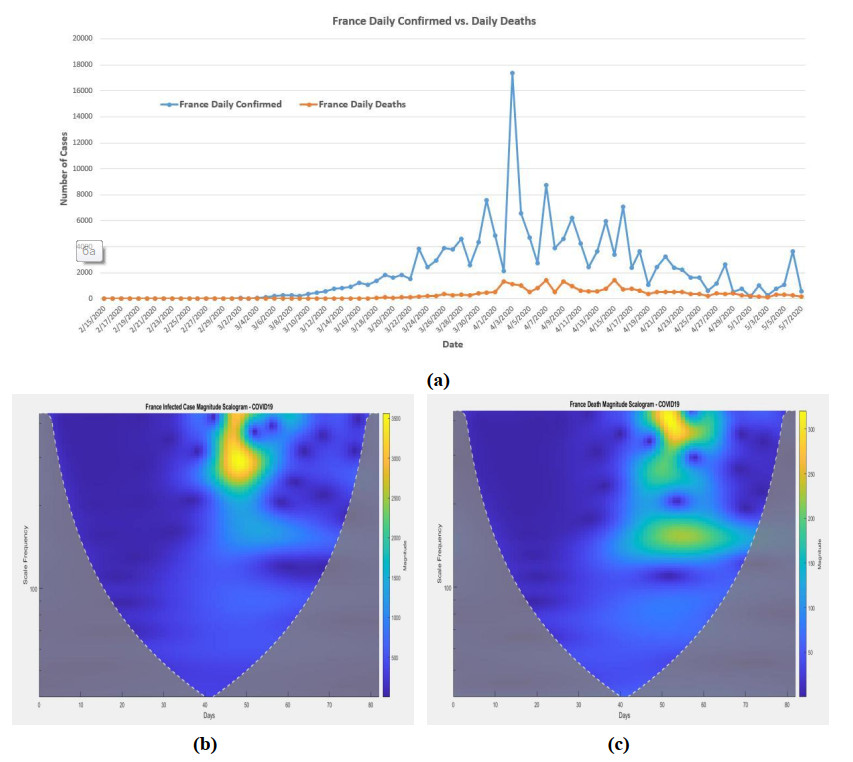
3.5. In France

The Morse wavelet analysis is also applied to France daily infected cases and deaths. They are shown in Figure 6b, c. The highest spreading peak (magnitude 3000 to 3500) was happened around the scale 235 to 412 from day 47 (4/1/2020) to day 53 (4/7/2020). The medium spreading magnitude (2000 to 2500) was happened from day 42 (3/27/2020) to day 56 (4/10/2020) with different scales.

Figure 6. (a): COVID19—France daily infected cases and deaths, the date is from 2/15/2020 to 5/7/2020. (b): COVID19—France daily infected cases wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020. (c): COVID19—France daily deaths wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020.

DownLoad: Full-Size Img PowerPoint

From the death magnitude scalogram (Figure 6c), the highest magnitude (280 to 320) of death was happened around the scale 329 to 412 from day 49 (4/3/2020) to day 55 (4/9/2020). After day 45 (3/30/2020), the medium magnitude 200 to 250 was also the threat with different scale.

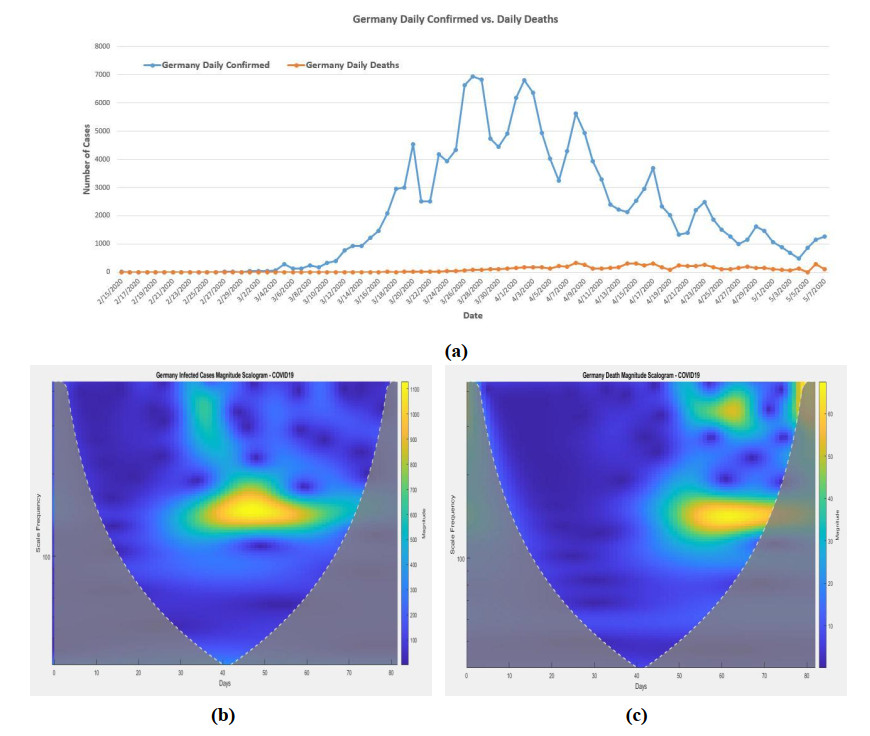
3.6. In Germany

The Morse wavelet analysis is also applied to Germany daily infected cases and deaths. They are shown in Figure 7b, c. The highest spreading peak (magnitude about 1000 to 1100) was happened around the scale 137 to 164 from day 38 (3/23/2020) to day 58 (4/12/2020). The medium spreading magnitude (750 to 900) was happened after day 32 (3/17/2020) with different scales.

Figure 7. (a): COVID19—Germany daily infected cases and deaths, the date is from 2/15/2020 to 5/7/2020. (b): COVID19—Germany daily infected cases wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020. (c): COVID19—Germany daily deaths wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020.

DownLoad: Full-Size Img PowerPoint

From the death magnitude scalogram (Figure 7c), the highest magnitude (60 to 65) of death was happened around the scale 137 to 149 from day 53 (4/7/2020) to day 72 (4/26/2020). Around day 79 (5/3/2020), the scale 412 also had the strong magnitude (around 60). After day 47 (4/1/2020), the medium magnitude from 40 to 60 was also the threat with different scale.

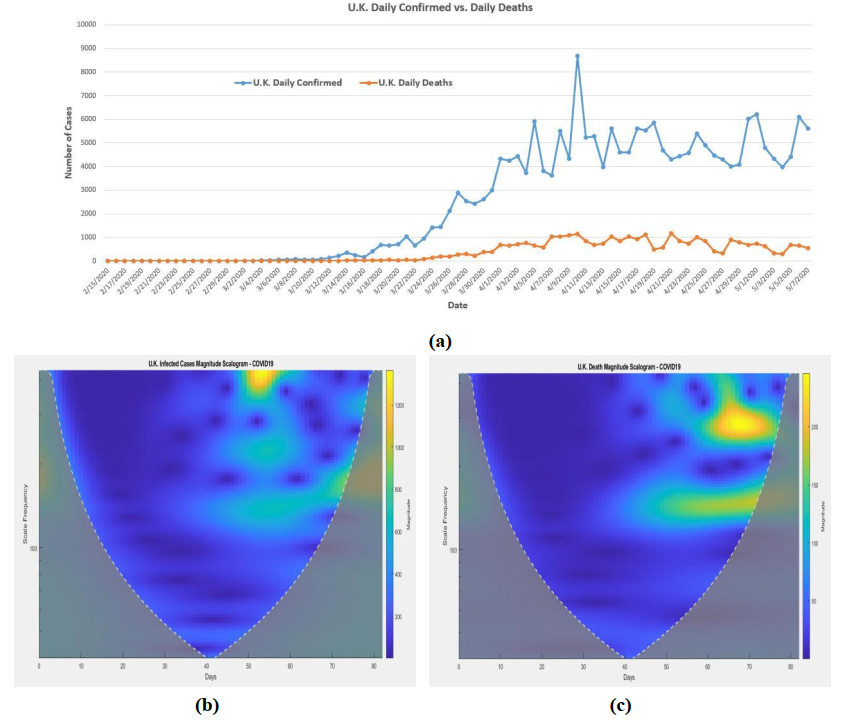
3.7. In U.K.

The Morse wavelet analysis is also applied to U.K. daily infected cases and deaths. They are shown in Figure 8b, c. The highest spreading peak (magnitude about 1200 to 1300) was happened around the scale around 412 from day 50 (4/4/2020) to 54 (4/8/2020). The medium spreading magnitude (around 800 to 1100) was happened after day 46 (3/31/2020) with different scales.

Figure 8. (a): COVID19—U.K. daily infected cases and deaths, the date is from 2/15/2020 to 5/7/2020. (b): COVID19—U.K. daily infected cases wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020. (c): COVID19—U.K. daily deaths wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020.

DownLoad: Full-Size Img PowerPoint

From the death magnitude scalogram (Figure 8c), the highest magnitude (200 to 250) of death was happened around the scale 273 to 329 from day 63 (4/17/2020) to day 74 (4/28/2020). There was a strong medium magnitude (150 to 200) happened after day 50 (4/4/2020) with different scales.

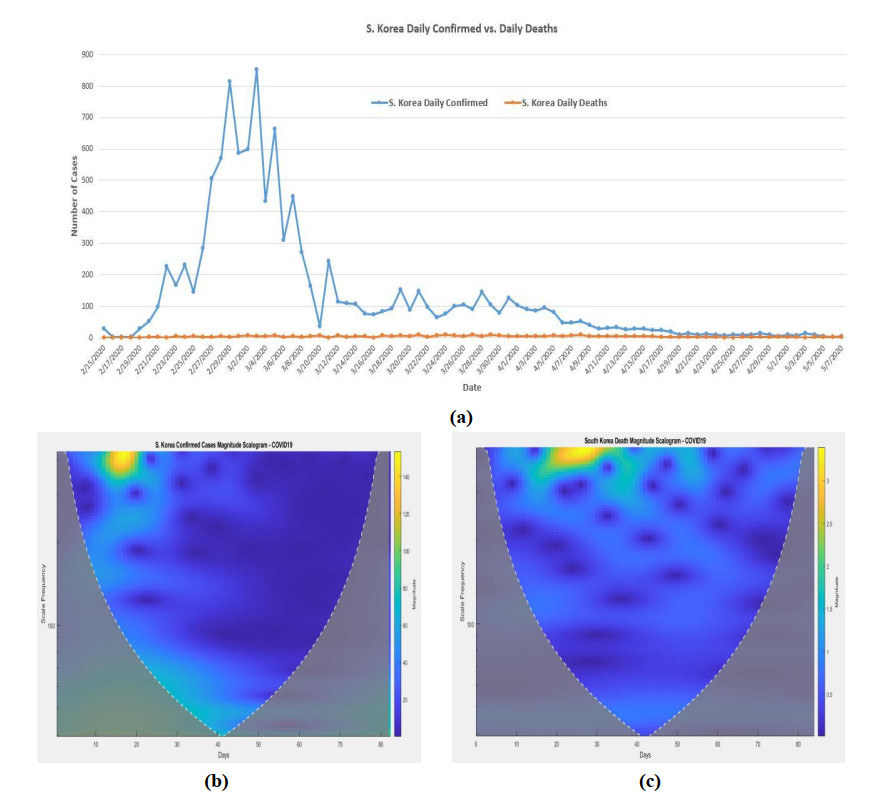
3.8. In South Korea

The Morse wavelet analysis is also applied to South Korea daily infected cases and deaths. They are shown in Figure 9b, c. The highest spreading peak (magnitude about 140 to 150) was happened around the scale 412 from day 14 (2/28/2020) to day 19 (3/3/2020).

Figure 9. (a): COVID19—South Korea daily infected cases and deaths, the date is from 2/15/2020 to 5/7/2020. (b): COVID19—South Korea daily infected cases wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020. (c): COVID19—South Korea daily deaths wavelet magnitude scalogram, the date is from 2/15/2020 to 5/7/2020.

DownLoad: Full-Size Img PowerPoint

From the death magnitude scalogram (Figure 9c), the highest magnitude (around 3.5) of death was happened around the scale 412 from day 20 (3/4/2020) to day 31 (3/16/2020).

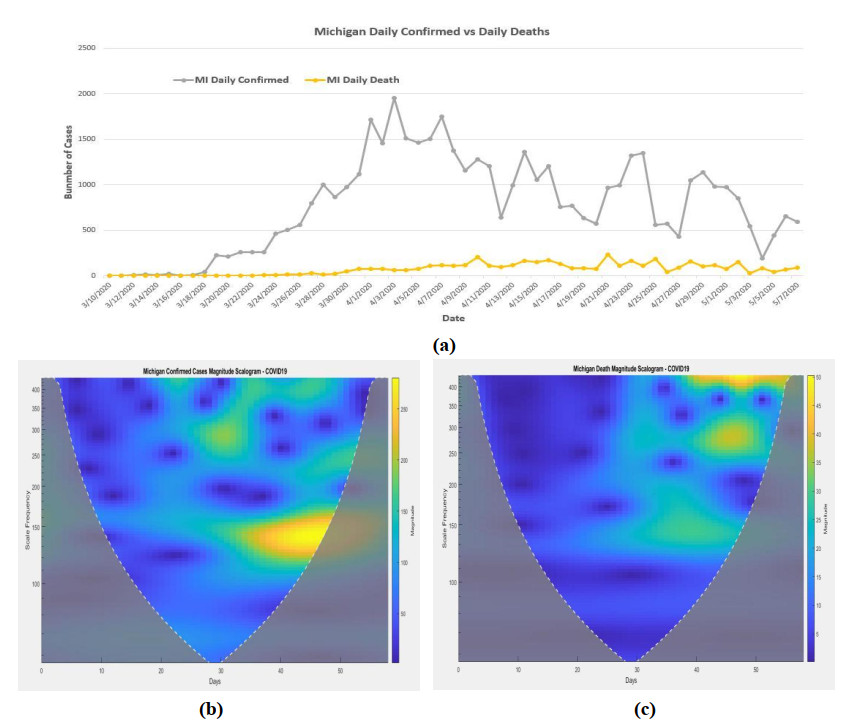
3.9. In Michigan

The Morse wavelet analysis is also applied to Michigan daily infected cases and deaths. They are shown in Figure 10b, c. The highest spreading peak (magnitude about 250 to 275) was happened around the scale 127 to 160 from day 36 (4/14/2020) to day 47 (4/25/2020). The medium spreading magnitude (around 150 to 200) was happened after day 22 (3/31/2020) with different scales.

Figure 10. (a): COVID19—Michigan daily infected cases and deaths, the date is from 3/10/2020 to 5/7/2020. (b): COVID19—Michigan daily infected cases wavelet magnitude scalogram, the date is from 3/10/2020 to 5/7/2020. (c): COVID19—Michigan daily deaths wavelet magnitude scalogram, the date is from 3/10/2020 to 5/7/2020.

DownLoad: Full-Size Img PowerPoint

From the death magnitude scalogram (Figure 10c), the highest magnitude (45 to 50) of death was happened around the scale 412 from day 42 (4/20/2020) to day 51 (4/29/2020). There was a strong medium magnitude (35 to 40) with scale 235 to 325 also happened from day 42 (4/20/2020) to day 51 (4/29/2020). After day 30 (4/8/2020), the medium magnitude around 30 was also the threat with different scale.

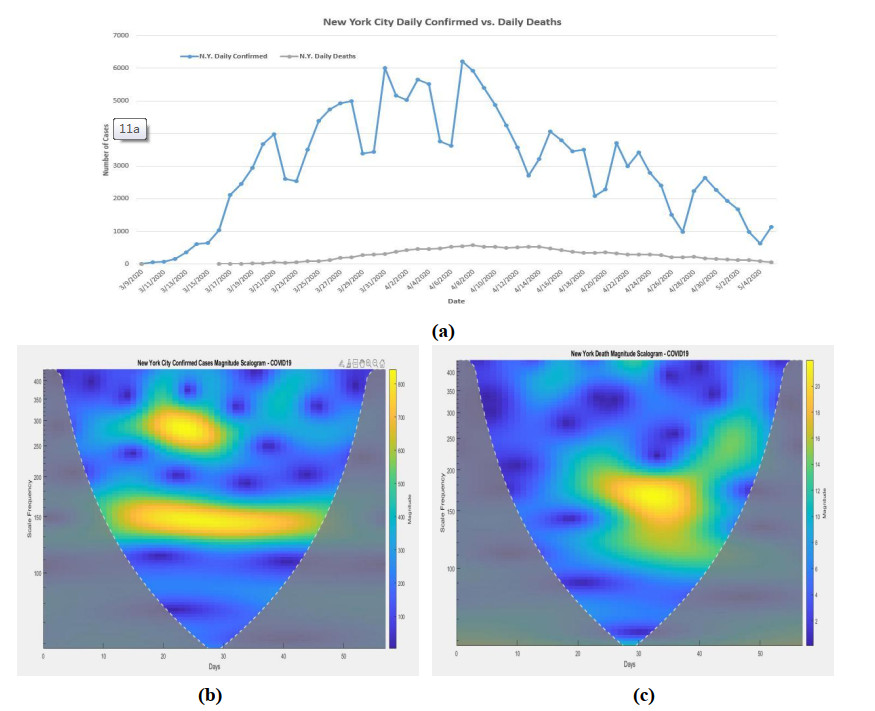
3.10. In New York City

The Morse wavelet analysis is also applied to New York City daily infected cases and deaths. They are shown in Figure 11b, c. The highest spreading peak (magnitude 700 to 800) was happened around the scale 137 to 164 from day 12 (3/20/2020) to day 46 (4/23/2020). There was another peak around scale 236 to 277 with magnitude around 700 to 800 from day 16 (3/24/2020) to day 32 (4/9/2020). New York City had the longest spreading span with high magnitude. Form day 10 (3/18/2020) to day 46 (4/23/2020) the medium magnitude 500 to 650 were spreading in different scales.

Figure 11. (a): COVID19—New York City daily infected cases and deaths, the date is from 3/9/2020 to 5/5/2020. (b): COVID19—New York City daily infected cases wavelet magnitude scalogram, the date is from 3/9/2020 to 5/5/2020. (c): COVID19—New York City daily deaths wavelet magnitude scalogram, the date is from 3/9/2020 to 5/5/2020.

DownLoad: Full-Size Img PowerPoint

From the death magnitude scalogram (Figure 11c), the highest magnitude (18 to 22) of death was happened around the scale 137 to 183 from day 24 (4/1/2020) to day 40 (4/17/2020). After day 20 (3/28/2020), the medium magnitude around 14 to 18 was also the threat with different scale.

4. Discussions

From the wavelet analysis presented above, we conclude that the wavelet variance (spectrum) of COVID19 spreading and deaths can be easily seen by magnitude scalogram plots. These plots show not only the magnitude of the spreading and death, but also the scale (frequency) of the spreading and death at specific time period. These wavelet spectrum analysis can be potentially useful to assist policy makers for designing containment strategies. Also comparing the magnitude scalogram between different places, we may evaluate and compare the effectiveness of the COVID19 mitigation strategies.

U.S.A has the highest spreading and death magnitude comparing to other countries. China had a high magnitude at the earlier stage of the spreading, so did South Korea, but South Korea has a much smaller magnitude. The European countries and U.S.A. had high magnitude spreading at the later stage. New York City had the longest spreading span period with a high magnitude. The spreading scale of epidemic waves are different from different places, for example, at the peak magnitude, China had the scale 329 to 434; U.S.A had the scale 137 to 183; Spain, Germany and New York City had the same spreading scale which was 137 to 164; U.K., Spain and South Korea also had the same scale 412; Italy and Michigan had a similar scale; France and New York City have a similar scale.

The summary of wavelet analysis is given in Table 1.

Table 1. The summary of wavelet magnitude, scale and time for daily infected cases and deaths at China, U.S.A., Spain, Italy, France, Germany, U.K., South Korea, Michigan and New York City.

Countries/Regions	Spreading Pattern
	Highest Magnitude			Medium Magnitude
	Magnitude	Scale	Time Period	Magnitude	Scale	Time Period
China	2000 to 2500	329 to 434	2/12	1500 to 2000	189 to 329	2/12
U.S.A	4000 to 4500	137 to 183	4/25 to 4/28	3000	329	5/2
U.S.A	4000 to 4500	137 to 183	4/25 to 4/28	1500 to 2500	149	after 3/25
Spain	900 to 1070	137 to 164	4/7 to 4/27	600 to 700	Varies Scale	3/20 to 5/1
Spain	900 to 1070	412	4/14 to 4/24	600 to 700	Varies Scale	3/20 to 5/1
Italy	600 to 700	126 to 164	3/17 to 4/9	400	Varies Scale	3/12 to 4/26
France	3000 to 3500	235 to 412	4/1 to 4/7	2000 to 2500	Varies Scale	3/27 to 4/10
Germany	1000 to 1100	137 to 164	3/23 to 4/12	750 to 900	Varies Scale	after 3/17
U.K.	1200 to 1300	412	4/4 to 4/8	800 to 1100	Varies Scale	after 3/31
South Korea	140 to 150	412	2/28 to 3/3
Michigan	250 to 275	127 to 160	4/14 to 4/25	150 to 200	Varies Scale	after 3/31
New York City	700 to 800	137 to 164	3/20 to 4/23	500 to 650	Varies Scale	3/18 to 4/23
New York City	700 to 800	236 to 277	3/24 to 4/9	500 to 650	Varies Scale	3/18 to 4/23
Countries/Regions	Death Pattern
	Highest Magnitude			Medium Magnitude
	Magnitude	Scale	Time Period	Magnitude	Scale	Time Period
China	320	329 to 434	4/17	200 to 250	206 to 329	4/13 to 4/19
U.S.A	500 to 550	137 to 164	4/27 to 4/29	350 to 400	274	after 5/2
U.S.A	500 to 550	137 to 164	4/27 to 4/29	350 to 400	150	after 4/4
Spain	70 to 80	274 to 411	4/11 to 4/19	50	Varies scale	after3/15
Spain	70 to 80	42	3/25	50	Varies scale	after3/15
Italy	75 to 85	274 to 329	3/20 to 3/30	60 to 70	Varies scale	after 3/15
Italy	75 to 85	235 to 274	4/26 to 5/1	60 to 70	Varies scale	after 3/15
France	280 to 320	329 to 412	4/3 to 4/9	200 to 250	Varies scale	after 3/30
Germany	60 to 65	137 to 149	4/7 to 4/26	60	412	5/3
Germany	60 to 65	137 to 149	4/7 to 4/26	40 to 60	Varies scale	after 4/1
U.K.	200 to 250	273 to 329	4/17 to 4/28	150 to 200	Varies scale	after 4/4
South Korea	3.5	412	3/4 to 3/16
Michigan	45 to 50	412	4/20 to 4/29	35 to 40	235 to 325	4/20 to 4/29
Michigan	45 to 50	412	4/20 to 4/29	30	Varies scale	after 4/8
New York City	18 to 22	137 to 183	4/1 to 4/17	14to 18	Varies scale	after 3/28

| Show Table

DownLoad: CSV

Also as we mentioned in section 2, the spreading and death jumps can be easily identified from the colorful plots of magnitude scalogram.

In this paper, the generalize Morse wavelet was used for our analysis because it is good for the modulated signals, but it is worthwhile to apply other orthogonal wavelets such as Daubechies in the study, and the wavelet multiresolution analysis should be explored in future studies.

5. Conclusions

The aim of this paper is to characterize the spreading and death waves for COVID19 by using the Morse wavelet analysis. The wavelet magnitude scalogram is the most simple and colorful way to explore the scale (frequency) and magnitude (energy) at the specific time period. The wavelet analysis can extract the useful information for the COVID19 spreading and death from time series data. By using the wavelet transform, this study hopes to bring a novel view to study the COVID19 spreading and death, and help the public health professionals to concentrate on the scale with high magnitude of spreading and death. The comparative analysis may help the policy makers learn from their counterparts, and make more evidence-based decision in our future fights against COVID19.

Acknowledgments

The author appreciates the data which was provided by the website in reference ^[1,2,17], and thanks MathWorks for providing the Wavelet analysis in Matlab package.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

[1]	WorldOMeters. Available from: https://www.worldometers.info/coronavirus/country/us/.
[2]	Click On Detroit News. Available from: https://www.clickondetroit.com/news/local/2020/03/20/michigan-covid-19-data-tracking-case-count-cases-by-county-deaths-cases-by-age-tests/.
[3]	Cazelles B, Cazelles K and Chavez M, (2014) Wavelet analysis in ecology and epidemiology: impact of statistical tests. J. R. Soc. Interface 11: 20130585.
[4]	Grenfell BT, Bjø rnstad ON and Kappey J, (2001) Travelling waves and spatial hierarchies in measles epidemics. Nature 414: 716-723.
[5]	Mathlab wavelet help tutorial. MathWorks.
[6]	Olhede SC and Walden AT, (2002) Generalized morse wavelets. IEEE Trans. Signal Proc. 50: 2661-2670.
[7]	Lilly JM and Olhede SC, (2009) Higher-order properties of analytic wavelets. IEEE Trans. Signal Proc. 57: 146-160.
[8]	Lilly JM and Olhede SC, (2010) On the analytic wavelet transform. IEEE Trans. Infor. Theory 56: 4135-4156.
[9]	Lilly JM and Olhede SC, Generalized Morse wavelets as a superfamily of analytic wavelets. IEEE Trans. Signal Proc. 60: 6036-6041.
[10]	Lilly JM, (2016) jLab: A data analysis package for Matlab, version 1.6.2. Available from: http://www.jmlilly.net/jmlsoft.html.
[11]	Lilly JM, (2017) Element analysis: a wavelet-based method for analysing time-localized events in noisy time series. Proc. R. Soc. A 473: 20160776.
[12]	Wachowiak MP, Wachowiak-Smolíková R, Johnson MJ, et al. (2018) Quantitative feature analysis of continuous analytic wavelet transforms of electrocardiography and electromyography. Philos. Trans. A Math. Phys. Eng. Sci. 376: 20170250.
[13]	Wang Y, (1997) Coupling of Small Scale Turbulence Near the Ground to Large Eddy Structures in a Desert Boundary-Layer. Master of Science thesis, University of Connecticut.
[14]	Miller DR, Wang Y and Cionco R, (1997) Ground Level Gust Frequency Coupled to PBL Large Eddies, in Proceeding of 12th Symposium on Boundary Layers and Turbulence. University of British Columbia, Vancouver, BC, Canada.
[15]	Miller DR, Wang Y and Cionco R, (1997) Detecting of PBL Forcing of Ground Level Winds in a Desert Using Wavelet Analysis Methods, in DTIC ADA344056: Proceedings of the 1997 Battlespace Atmospherics Conference.
[16]	Mallat S, (1989) A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 11: 674-693.
[17]	New York City Gov.. Available from: https://www1.nyc.gov/site/doh/covid/covid-19-data.page.
[18]	Wang Y, (2020) Use NHPP (Non-Homogenous Poisson Process) Crow-AMSAA method to model the spreading and death rate of the COVID 19. Presented in the SCIENTIFIC PERSPECTIVESON COVID-19 Conference on May 4th, 2020, Scientific Online Conference.
[19]	Wang Y, (2020) Predict new cases of the coronavirus 19; in Michigan, U.S.A. or other countries using Crow-AMSAA method. Infect. Dis. Model. 5: 459-477.

This article has been cited by:

Chiuhsiang Joe Lin, Rio Prasetyo Lukodono, Sustainable Human–Robot Collaboration Based on Human Intention Classification, 2021, 13, 2071-1050, 5990, 10.3390/su13115990

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)