Effect of specimen size on natural vibration of open hole copper/glass-reinforced epoxy laminate composites

Abbreviations: ${\mathrm{\varnothing }}_{o}$: Phase angle; ${A}_{o}$: The amplitude of the displacement; $\ddot{x\mathrm{ }}$: Acceleration component; $\dot{x}$: Velocity component; ${\omega }_{n}$: The natural frequency in rad/s; E: Young’s modulus; y: The eigenvector of the system; λ: The frequency factor; Ρ1 (Ω·m): Electrical resistivity; ψ: Eigenvalues; $F$: Spring force; $c$: Damping constant; $k$: Spring stiffness; $m$: Mass; $t$, $\mathrm{\beta }$: Time; $x$: Displacement; $\alpha$: Thermal of linear expansion; $q$, $\dot{q}$, $\ddot{q}$: Displacement, Velocity, and acceleration in generalized coordinate; Q: Quality factor; ${F}_{damping}$: Damped force: ${f}_{n}$: Natural frequency in Hz; ρ: Density; h: Plate thickness; l: Plate length; D: Rectangular shape flexural stiffness

1.   Introduction

Recently, hybrid composite materials have been widely used in the electronics industry in the form of precision Electromechanical Systems (MEMS) ^[1]. Mechanical and thermal properties strongly influence MEMS performance from a reliable perspective ^[2]. Although there are many studies devoted to the processes of modeling, designing, selecting, and manufacturing composite materials used as MEMS, their reliability, durability, and fracture behavior characteristics during operating conditions are still not fully reported ^[2].

Hassan et al. ^[1] predicted fatigue behavior in the thin copper layer connected to the steel substrate using two types of bonding techniques; one is epoxy resin and the other is diffusion bond. Their results showed that fatigue performance is affected by diffusion technology. Nevertheless, the study did not involve the effect of size and scaling, moreover vibration.

The critical J-integral (Jc) in elastic-plastic fracture of the polysilicon sample was studied by Ballarini et al. ^[2]. These samples are formed similarly to MEMS. The results indicated that the energy released from these polysilicon samples is four times greater than that in one crystal. On the other hand, the fracture resistance of thin films used in devices (MEMS) ^[3] was examined. Fracture resistance behaviors were measured for the ultra-nano-crystal diamond. This study demonstrated that the initial fracture of the blunt crack is larger than that of a sharp crack tip, it is Given the value of a correction coefficient for the material using the model of Drory et al. ^[4].

The finite element analysis (FEA) of experimental results ^[5] was used to measure the fracture resistance of silicon used in (MEMS) devices. A special sharp mechanism was used to ensure accurate prediction of crack intimation and propagation. Contrary to the work of Sharp et al. ^[6] and Tsuchiya et al. ^[7], fracture resistance of (MEMS) materials was measured with an infinite radius of diameter when their sample was fractured using a piezoelectric load cell.

A simple numerical modeling using an advanced finite element method was derived to measure the EWF parameters ^[8] for a thin aluminum sheet. Other work ^[9,10,11] has been reported on the effect of the specimen size of the copper-layer attached to a substrate of steel sheet which is considered to be a semi-fragile material.

The effect size is defined based on the nominal resistance of Quasi-brittle material as the decrease in resistance concerning the sample size; this is the fundamental problem of all physical theory without understanding the effect of scale or scale effect, there is no valuable theory. ^{[12,13,14,15,16,17,18]}. The effect of size on structural resistance refers to the modification of the nominal resistance concerning the dimensions of the structure while maintaining the geometric proportions and constant material ^[19]. This phenomenon of composite materials is not well understood, if not taken into account when designing a composite structure, this could lead to premature catastrophic failure ^[20].

The achievement of the vibrating properties of these materials is very important in engineering to achieve an excellent and safe design ^[21,22]. Accordingly, these types of compounds are distinguished for their superior strength and the high hardness-to-weight ratio ^[21]. Moreover, the effect of a cracked plate is not considered anymore.

Kallannavar and Kattimani ^[23] numerically investigated the natural frequency of composite laminates and face sheet core material. It is used graphite fibre reinforced epoxy of stacking (0/45/−45/90) s, (0/0/30/−30) s, and (45/−45/−45/45) s, alumina alloy 2024 was used as a core material. The numerical study was through finite element analysis through ANSYS. Effect of fiber orientation and aspect ratio were reported, it was also concluded that all clamped boundary conditions were more suitable for high frequencies however, cantilever beam boundary conditions were more convents at a lower frequency. The study lack of any experimental validation, also the interaction between core and face sheet material did not consider.

Sharm et al. ^[24] built a finite element model to estimate the natural frequency of functionally graded material. They studied the effect of hygrothermal conditions such as; moisture, temperature, volume fraction, and length to thickness ratio. It is concluded that moisture content highly affected the eigenfrequency, while, relatively little effect in other conditions. The model might be recommended for structural health monitoring perspective. The vibration response of thick composite laminates and honeycomb sandwich panels had been studied by Chronopoulos et al. ^[25]. It was used as a finite element method to predict the vibration response. The effect of layer debonding was obtained. The results were experimentally evaluation, it was reported that the results were accurate and more suitable for composite material.

Kleverson et al. ^[26] measured the natural frequency, damping ratio, and shape mode of honeycomb sandwich panel for aerospace purpose applications. The experimental measurement was through a well-known modal test. A laser Doppler vibrometer was used. The main goal of these experimental data was to validate the finite element modal created using Ansys software. It was assumed that the interior structure interfaces for the composite material had little effect on the vibration response which was an unlogic suggestion. However, the results gave good agreement with experimental results in relatively small errors. But this is higher in the case of torsional modes. They explained that to that the panel is thin. This was not true in all cases as most laminated plated composite is thin and interaction in the interior plies.

Not only finite element was used in the simulation of modal analysis but there were other mathematical models. Suragimath ^[27] used MATLAB computational code to measure the modal analysis parameter such as; natural frequency, damping ratio. While the mode shapes were estimated using finite element analysis using ANSYS Software. The study was carried out for glass fiber, carbon fiber, and graphite fiber reinforced epoxy composite panel. The calculation based on Euler’s–Bernoulli beam theory at different boundary conditions. It was reported that fixed-fixed boundary conditions give higher frequency, also the composite panel reinforced by carbone fiber gave higher frequency than graphite fiber and glass fiber. There was a lack of study for the effect of interconnection between layers and the effect of specimen sizes.

The orientation of fiber in the composite panel had been studied numerically by Samyal et al. ^[28]. As in the previous work, different boundary condition was investigated, the results suggested that the optimal fiber orientation and their effect, but the study lack of experimental validation of the supposed problems.

Pingolkar and Suresha ^[29] numerically investigated the free vibration of a laminated plate using the ANSYS finite element package. They studied the effect of different stacking sequences, the fibre size fraction, and aspect ratios, thus obtaining good compatibility between the obtained frequencies and the published experimental results. However, the study lacked information to understand damping ratios for other substances.

On the other hand, Jensen et al. ^[30] analyzed the effects of unbalanced sheets on the natural frequency of a compound cantilever beam using the Raleigh Ritz model and gave an excellent report on the use of FEA and the experimental results of their study.

Srinivasa et al. ^[31] studied the number and experimentation of the natural frequencies of isotropic and compound inclined plates. They studied the effect of tilt angle, stacking sequence, and aspect ratio of the fibres on the natural frequency, and reported excellent numerical results for finite elements compared to experimental results. Moreover, they reported that the natural frequency increases with increasing angle of inclination.

Malekzadeh and Zarei ^[21] have analyzed the free vibration behaviors of sophisticated thin and thick advanced composite chips reinforced with carbon nanotubes. They studied the effect of lamination and various engineering parameters on the behavior of this type of material under free vibrations. They stated that their results will be used as a basis for future studies.

Abdellah et al. ^[32] investigated numerically and experimentally the vibration response of composite laminated correlated to other monotonic metal like; aluminum and steel. The modal analysis results compared with Finite element modeling and the results were in good agreement, while in another study ^[33] the modal analysis extended to Kevlar and carbon fibre reinforced polymer. In these two studies, the results were about composite laminates that are the main structural material of the aerospace industry but these studies did not consider the effect of crack on the vibration and consider the application of such material in biomedical fields.

2.   The novelty and objects of the present study

The main goals of the present study can be summarized in the following items:

1.Experimentally measuring size effect or scaling effect on the dynamic response of copper/glass-reinforced epoxy laminate composites (CGRELC) which are used in MEMS applications using modal analysis method. As there is no work available about size effect in case of vibration, this study reveals the effect of material’ size on vibration mode shapes in the presence of holes. As known vibration is serious in the case of industrial applications where there are fluctuations of applied loads especially in aerospace MEMS applications which most vibration would be damped vibration and due to stressed parts. In the case of aerospace applications, airflow at very high in the air with the high velocity of airplanes makes serious fluctuation of vibration which affect badly on the electronic ships of airplanes, which gives important need to study the vibration of such material with scaled holes. Similarly, in MEMS composites, electrical current fluctuations arise serious vibrations which affect the electrical performance of MEMS by increasing their electrical resistivity.

2.Building a finite element model to predict the natural frequencies shape modes, as well as Misses, stress effect regions.

This paper is written as follows: In the first paragraph the modal analysis is summarized, then the experimental procedures are outlined, while the Finite element model is contracted in the third paragraph and finally, the results are presented and discussed.

3.   Mathematical modal analysis

The mathematical solution for vibration respect to a plate with a hole can be in the coefficient of damping (c) and the coefficient of elasticity (k) or flexural stiffness (D) ^[34]. The linear damping force can be measured as the following in Eq 1:

where ($Q = \frac{\omega t}{2\pi }$) i is the equality factor and $\dot{q}$ is the generalised velocity the generalized equation of motion for damped simple harmonic motion Eq 2 can be as:

The simple harmonic oscillator Lagrangian (Eq 3) with characteristic frequency;

where (D) plate stiffness, ($F$) is the coefficient of the kinetic energy term, and thus F > 0 holds. Thus, rescale the time units to define; ($\mathrm{\beta } = \sqrt{\left|1/{\omega }^{2}\right|} = \sqrt{\left|\frac{F}{D}\right|}$) and time coordinate ($t = \mathrm{\beta }\mathrm{\tau }$). Such the Q component can be ($Q = \frac{\omega }{b/m}$) and ($\omega = \sqrt{\frac{k}{m}}$) is the natural frequency in rad/sec.

Where x is the amplitude or deviation of the oscillating motion (m), ẋ is the velocity (m/s), ẍ is the acceleration (m/s²), F is the excitation force (N), ($\omega$) is the natural frequency of the mode (rad/sec), and stiffness constant of the plate (k) or (D) and damping coefficient or damping constant (c) of the system. Then it is found that (Q) increases as the spring constant or mass increases relative to the damping constant (c). to understand the physical meaning of Q, it is should to rewriting equations in dimensional form.

The equation of motion of a mechanical vibrated system subject to a linear damping force is measured as:

By divided Eq 4 by component ($Q$), one can obtain the expression for damping force Eq 5;

By divided Eq 5 by component ($m$), it is estimated natural frequency in Eq 6;

Equation 5 can be rewritten as ($\ddot{mx}+{F}_{damping}+{\omega }^{2}mx = 0$) for just illustration.

The natural frequency (Eq 7) in term of non-dimensional vibration into more familiar units (Hz) can be measured as ^[35]:

where h is plate specimen thickness, $l$ plate length, $\rho$ material density, and D is the cantilever flexural stiffness (Eq 8) in the present study:

where E young’s modulus and $\nu$ is passion young’s modulus, and ($\lambda$) is a non-dimensional frequency factor which is for cantilever plate ^[36]. The problem with open holes will be changed according to D as the open holes specimen has different strengths this gives different young’s modulus. Thus, the effect of holes may be model using the coefficient of damping (c) and the plate stiffness D ^[37,38].

4.   Experimental work

4.1.   Materials and processing

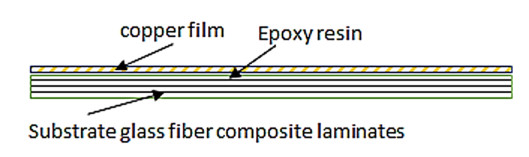
Figure 1 illustrates the composite structure used in this study. The sample consists of a thin laminate of epoxy/fiberglass reinforced composite with a thickness of 1.5 mm and a thin copper film adhered to the base of the sheets of epoxy resin fiberglass. A thin layer of copper up to 50 microns and 24 layers of woven fiberglass is used to form this compound structure. Tables 1–3 list the chemical composition, electrical and mechanical properties of copper and epoxy, respectively. Six different hole diameters 2, 4, 6, 8, 10, and 12 mm are carried out in the specimens with scaling with the width, which keeps the diameter to width ratio constant (1/6) ^[39] (see Figure 2).

Figure 1.  Schematic drawing of MEMS components.

DownLoad: Full-Size Img PowerPoint

Table 1.  Chemical composition of copper film and base glass fiber ^[40].

Phase	Ni	Sn	Al	Zn	MN	Pb	Fe
Copper film	0.0005 >	0.0005 >	0.0005 >	0.0005 >	0.0005 >	0.0005 >	0.0005 >
Glass fiber	E-glass-roving-pl = 2200 gm/km
Epoxy	Resin-Kemapoxy (150RGL)

---

 | Show Table

DownLoad: CSV

Table 2.  Mechanical properties ^[40].

Phase	Young modulus, E (GPa)	Thermal of linear expansion, $\mathit{\alpha }/\mathit{K}$
Glass fiber	24 (Length Wise), 21 (Cross Wise)	4.0 × 10−5
Copper film	123	1.68 × 10−5
Epoxy	1.2–4.5	-

---

 | Show Table

DownLoad: CSV

Table 3.  Electrical properties of MEMES ^[40].

Phase	Electrical resistivity, ρ (Ω·m)	Dielectric strength, V$/\mathit{m}\mathit{i}\mathit{l}$
Copper film	1.68 × 10−8 [22]	-
Glass fiber	10 [23]	> 762 [23]
Epoxy	> 1 × 105[24]	500 [24]

---

 | Show Table

DownLoad: CSV

Figure 2.  Sample of modal analysis test with holes.

DownLoad: Full-Size Img PowerPoint

4.2.   Vibration modal analysis

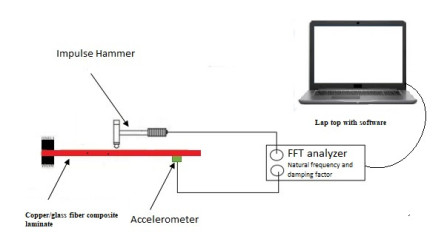
The free vibration test set consists of various equipment and tools, summarized as follows: Delta Tron High-Temperature Accelerometer (Bruel and Kjaer), type 4526, with a voltage sensitivity of 100 mV/g ± 10% used from 160 Hz and 25 kHz combined resonance frequency to measure sample response. The transducer was attached to the sample using beeswax. A shocker hammer (Bruel and Kjaer), type 8206, with a voltage sensitivity of 22 mV/N and a built-in power transformer with a pressure of a full power range of 220 N, was used to push the model through with a driving force. The hammerhead was made of hard plastic. This gives the start input frequency and magnitude for the modal setup (see Figure 3).

Figure 3.  A schematic drawing of measurement system set up.

DownLoad: Full-Size Img PowerPoint

To obtain the sample I/O data, a six-channel input unit, LAN-XI (Bruel and Kjaer) type 3050, was used with a frequency range of 51.2 kHz. Two input channels were used for taking measurements, one for the impact hammer and the other for the accelerometer.

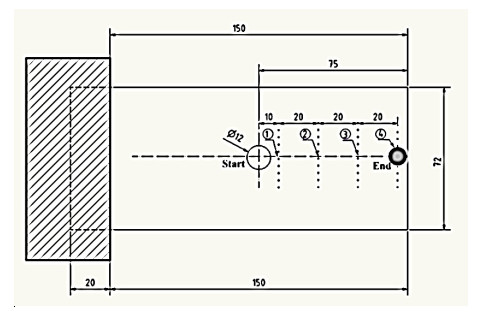
PULSE LabShop V13.5.0 (Bruel and Kjaer) containing 1-6 Ch closed licenses was used for fast Fourier transform analysis to create frequency response function curves (FRF) and cascading charts. Model parameters, such as natural frequencies, damping ratios, and mode shapes, were determined using the software. The test sample has a rectangular cross-section of 72 mm × 150 mm long was fixed to one end of an attachment so that it can be considered as a cantilever. The sample was attached securely to a steel plate and securely fastened. A stepwise sample with a hole-to-width ratio equal to 1/6; 2, 4, 6, 8, 10, and 12 mm is used (see Figure 3). The crash hammer and accelerometer were connected to the LAN XI using BNC cables and connectors, while the hardware unit was connected to a DELL laptop (Latitude E6400), which had a PULSE LabShop V13.5.0 with a LAN cable (see Figure 3). There are 20 different nodes in each sample, equally spaced 30 mm. To collect data, the transducer is assigned to node 20. In each sample, a mobile shock hammer test technique is applied to measure the response in all nodes, one at a time, using the program. The hammer acts as the system entry, while the accelerometer measures the system’s response at each node. Conditional parameters, such as natural frequencies and damping ratios, are extracted from the FRF curve at each node in different ways obtained using the program. Quadratic Selection Technology ^[35] is used to obtain different positioning shapes. The natural frequencies and damping ratios are taken at positions 1, 2, 3, and 4. The frequency is calculated for four possible modes ^{[17,18,41,42,43,44,45,46,47]}.

4.3.   Finite element method

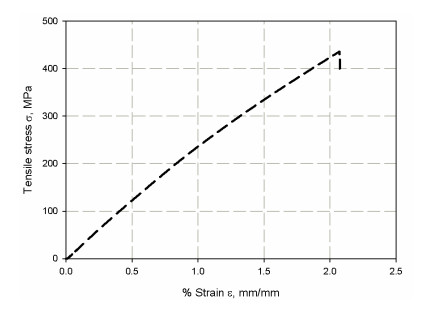
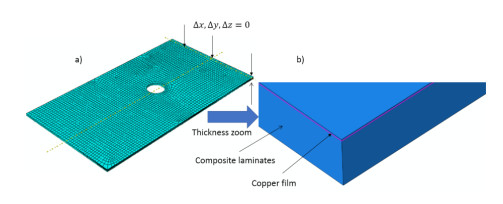
The vibration modal analysis is simulated using the finite element method. The model is simulated using two material copper thin film and woven glass fiber, the material mechanical properties are listed in Table 4 and illustrated in Figure 4, it is implemented as Elastic constant, these values are measured based on the rule of a mixture based on the volume fraction of matrix and epoxy using ignition removal technique. The model density depended on the amount of element removed, therefore, it is 1780, 1700, 1400, 1400, 1370, 1300 for each hole respectively. the model based on Lanczos criteria for eigensolver with acoustic structural coupling, it is out to measure the frequency at 4 stable modes. The open hole plates were meshed using a swept meshing technique which gives more accuracy. For 3-D stress element, an 8-node linear brick, reduced integration, hourglass control (C3D8R) is used. The total number of elements for each hole is 61558, 60699, 140275, 66013, 64792, 58280, respectively. Finite element mesh and boundary conation domain are shown in Figure 5. The one end is let to be free; the other end is constrained in all directions. The fixation at one end side of the cantilever beam. The copper thin film of 0.05 mm thickness attaches to the composite laminates plate using tie constrained technique as shown in (Figure 5b). The interaction between copper film and composite laminates does not consider. To select the optimized mesh density and element type; three refinements are selected (61558, 21442, 18438). The frequency factor for each mesh density is compared with the experimental results. The closer one is selected and described above. Also, the optimal number of modes were selected according to the closer average when compared with experimental results. Therefor just the first two modes are measured because these modes are the ones which size effect or scaling effect is observed. The algorithmic medial type is used with a hex-dominated shape.

Table 4.  Mechanical properties of glass-reinforced epoxy laminate composites.

Properties	Value
E1 (GPa)	12.5
E2 (GPa)	12.5
E3 (GPa)	2.8
G1, G2, G3 (GPa)	4.5
µ1, µ2, µ3	0.12

---

 | Show Table

DownLoad: CSV

Figure 4.  Tensile stress-strain curve for composite material (un notched specimens).

DownLoad: Full-Size Img PowerPoint

Figure 5.  Finite element domain (a) mesh domain and (b) boundary condition domain.

DownLoad: Full-Size Img PowerPoint

5.   Results and discussion

5.1.   Modal analysis

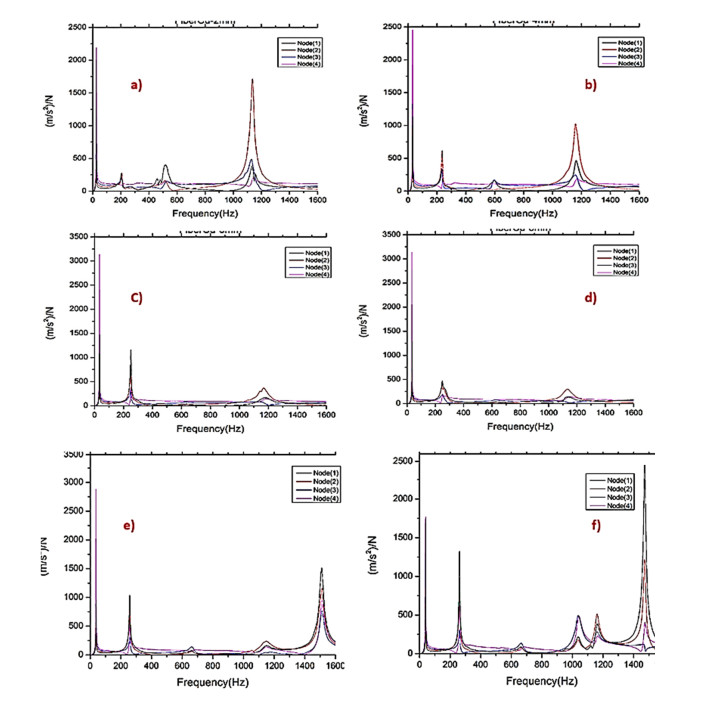
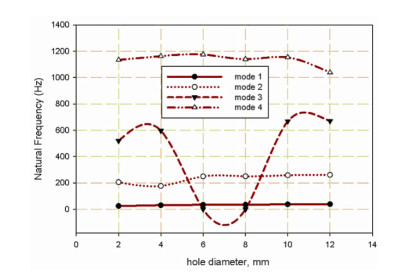
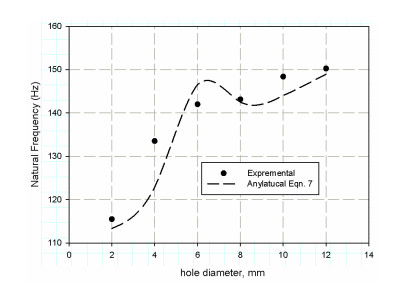
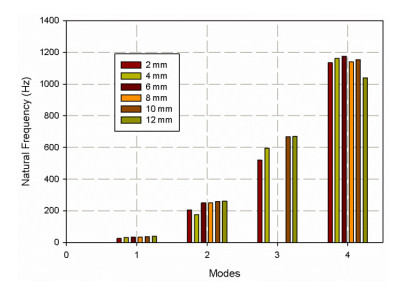
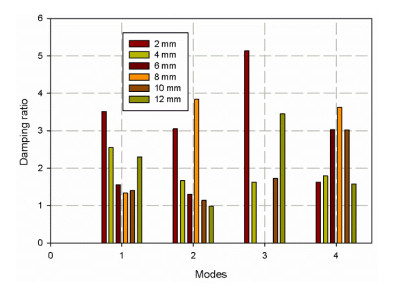
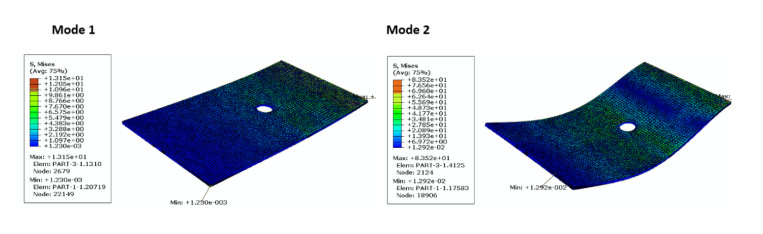
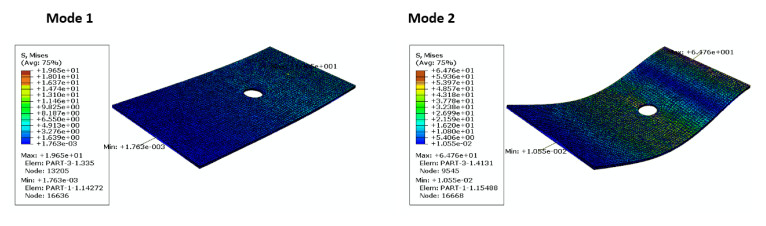
The investigation of experimental modal aims to determine the dynamic behavior, such as natural frequency, damping ratio, and mode shapes of the system configuration during the testing process. Natural frequencies and shapes with which the structure will magnify the influence of a load can be detected by modal analysis ^[48]. Through these analyses, the first step is to identify the normal frequencies and damping ratios, which is carried out by getting information from the frequency response function (FRF) curve. PULSE LabShop automatically supplies the necessary information for both natural frequencies and damping ratios after using different curve fitting. Natural frequency and damping ratios which are measured using a modal analysis of cantilever plate are listed in Tables 5–10 and modal magnitude shapes are shown in Figure 6. It is observed that for lower modes; the frequencies increase with increasing specimen size while for lager frequencies it is little affected. The same trends for damping ratios; increasing of holes leads to increased damping ratio, it is observed for the first two modes. It is seen in Figure 7 the specimen scaling or size effect give a variation in the natural frequencies and damping response. The size effect gives a dynamic response with the average values of natural frequencies of the two first modes 1, 2 (see Figure 8). And good acceptable results with the analytical data Eq 7. The results of the analytical data based on the non-dimensional frequency factor ($\lambda$). The frequency factors are calculated using FEM previously described and are listed in Table 11. Figure 9 show the results of the frequency factor ($\lambda$) with the two modes for each specimen holes. It is observed that the frequency factor direct proportionally to the mode increment. Moreover, the frequency factor increases with hole diameter increment. This the typically the size effect in dynamic response. The vibration wave vanished in case of mode 3 for 6 mm and 8 mm hole diameter (Figure 6), This may be attributed to the resulting absorption through the steel of fixation system this is the reason why it is increasing again in mode 4 and that these points are anti-resonances for the specific model. This observation cannot be found in the finite element model, because the model assumed a rigid body which does not affect the testing response. This variation is observed in bare curves Figures 10 and 11.

Table 5.  Natural frequencies and damping ratios of CGRELC of 2 mm hole diameter.

Node number	Mode 1		Mode 2		Mode 3		Mode 4
	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)
1	24	4.92	206	3.06	516	3.46	1133	.96
2	25	3.24	207	2.45	515	4.31	1137	1.03
3	25	3.38	205	3.67	528	7.64	1128	1.59
4	26	2.53	-	-	-	-	1141	2.94
Average	25	3.5175	206	3.06	519.66	5.1366	1134.75	1.63

---

 | Show Table

DownLoad: CSV

Table 6.  Natural frequencies and damping ratios of CGRELC of 4 mm hole diameter.

Nodenumber	Mode 1		Mode 2		Mode 3		Mode 4
	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)
1	31	2.82	236	1.45	597	-	1164	-
2	31	2.38	236	1.51	-	-	1158	1.43
3	31	2.96	234	1.8	596	3.25	1158	2.13
4	31	2.07	2.38	1.91	-	-	1171	3.61
Average	31	2.5575	177.095	1.6675	596.5	3.25	1162.75	1.7925

---

 | Show Table

DownLoad: CSV

Table 7.  Natural frequencies and damping ratios of CGRELC of 6 mm hole diameter.

Nodenumber	Mode 1		Mode 2		Mode 3		Mode 4
	Natural frequency (Hz)	Damping ratio(%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)
1	34	1.39	251	1.17	-	-	1185	3.4
2	34	1.73	249	1.61	-	-	1167	2.66
3	34	1.47	249	1.49	-	-	-	-
4	34	1.64	251	0.96	-	-	-	-
Average	34	1.5575	250	1.3075	0	0	1176	3.03

---

 | Show Table

DownLoad: CSV

Table 8.  Natural frequencies and damping ratios of CGRELC of 8 mm hole diameter.

Nodenumber	Mode 1		Mode 2		Mode 3		Mode 4
	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)
1	35	1.24	249	3.51	-	-	1133	2.89
2	35	1.26	248	5.61	-	-	1135	2.77
3	35	1.32	253	5.15	-	-	-	-
4	35	1.52	251	1.11	-	-	1152	5.21
Average	35	1.335	250.25	3.845	0	0	1140	3.62

---

 | Show Table

DownLoad: CSV

Table 9.  Natural frequencies and damping ratios of CGRELC of 10 mm hole diameter.

Nodenumber	Mode 1		Mode 2		Mode 3		Mode 4
	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)
1	38	1.55	258	1.12	661	2.48	1151	2.73
2	38	1.51	259	1.08	666	2.04	1149	2.98
3	38	1.33	258	1.52	663	2.4	1171	3.35
4	38	1.24	260	0.84	684	-	1148	3.04
Average	38	1.4075	258.75	1.14	668.5	1.73	1154.75	3.025

---

 | Show Table

DownLoad: CSV

Table 10.  Natural frequencies and damping ratios of CGRELC of 12 mm hole diameter.

Nodenumber	Mode 1		Mode 2		Mode 3		Mode 4
	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)	Natural frequency (Hz)	Damping ratio (%)
1	39	1.94	262	0.98	664	2.37	1038	1.47
2	39	2.29	261	0.95	668	2	1038	1.49
3	39	2.42	260	1.29	664	2.43	1038	1.79
4	40	2.55	262	0.72	684	7	1043	1.57
Average	39.25	2.3	261.25	0.985	670	3.45	1039.25	1.58

---

 | Show Table

DownLoad: CSV

Figure 6.  Frequency shape mod in frequency response for hole diameter (a) 2 mm, (b) 4 mm, (c) 6 mm, (d) 8 mm, (e) 10 mm, and (f) 12 mm.

DownLoad: Full-Size Img PowerPoint

Figure 7.  The relation between hole diameter and natural frequencies.

DownLoad: Full-Size Img PowerPoint

Figure 8.  Relation between hole diameter and average natural frequencies.

DownLoad: Full-Size Img PowerPoint

Table 11.  The frequency factor ($\lambda$) with various hole diameter.

Mode number	2 mm hole	4 mm hole	6 mm hole	8 mm hole	10 mm hole	12 mm hole
1	2.157382094	2.268324181	2.518593434	2.464181544	2.47719235	2.501362622
2	5.463216075	5.679072839	6.184986666	6.107650088	6.141138431	6.251503221

---

 | Show Table

DownLoad: CSV

Figure 9.  Relation between hole diameter and non-dimension frequencies factor ($\lambda$).

DownLoad: Full-Size Img PowerPoint

Figure 10.  Relation between vibration modes and natural frequencies.

DownLoad: Full-Size Img PowerPoint

Figure 11.  The relation between vibration modes and damping ratio.

DownLoad: Full-Size Img PowerPoint

The average value of first natural frequency and average damping ratios for mode 1 for the sample of 2, 4, 6, 8, 10, and 12 mm holes can be seen in Table 5. All the 4 node points show first resonance at 25, 31, 34, 34, 38, and 39.25 Hz for hole diameter respectively. The structural response at nodes 3, and 4 is high as compared to the other points because of their positions at the free end, this can be seen in Figure 6a. The dynamic response of that between the average frequency of first two modes ranges of 25–206, 31–177.095, 34–250, 35–251.25, 38–258.75, 39.25–261.25 Hz are very stable, for each hole diameter respectively, these are tabulated in Tables 5–10. While, in general, the damping ratio decrease with increasing hole size and scaling and it is observed for the first two modes. The damping ratio for specimens of 2, 4, 6, 8, 10, and 12 mm holes for all four nodes for the average of four modes (3.336), (1.910), (1.965), (2.93), (1.82), (2.078). The damping ratio gives an observable size effect trend for the first two modes.

It is clear of Table 11 that the value for the first two modes is stable and very close to that of Reference ^[36]. It is linearly increasing with mode increment. The frequency factor increases with hole diameter increment.

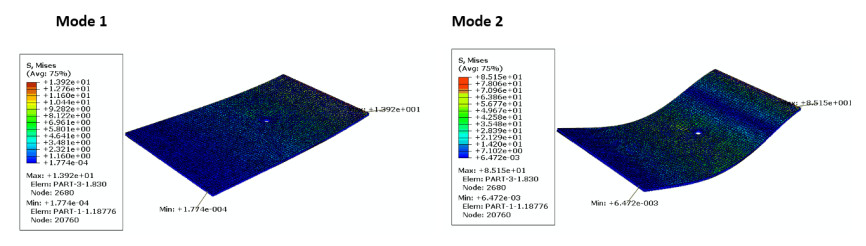
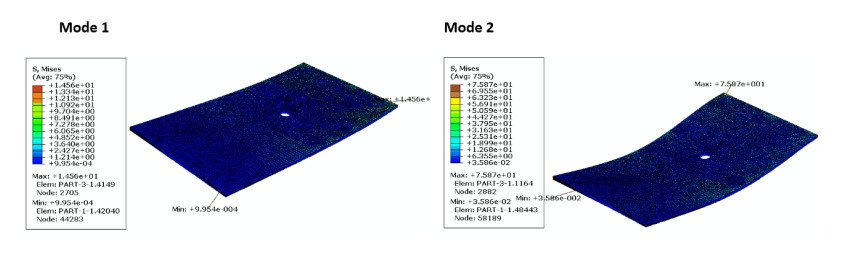
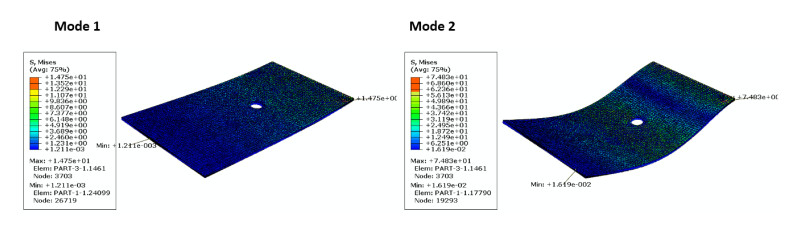
Finite element shape modes are illustrated in Figures 12–17, the number of curvatures is increased with higher modes. As the same material, all specimens take the same waviness and curvature in all modes, but the difference is in values of Mises stress. For specimen size of 2, 4, 6, 8, 10, and hole diameter, the maximum mises stress in modes 1 (red color) are 1.96, 1.3, 1.47, 1.45, 1.39, 1.7 MPa respectively and is nearly stable, while for mode 2 are 9.33, 8.515, 7.58, 7.48, 8.35, 6.47 MPa, it decreases with increasing specimen size. All maximum Mises stresses are near fixation end due to increase shear stress due to the increase of shear stress arising from clamping action. The minimum Mises stress (blue color) is located at the free end of the plate. Around the hole there is a medium region of Mises stress (green color) effect, this is because the hoe is considering as stress relives for the vibration waves. It is also clearly observed that the mises’ stress increase with mode increases.

Figure 12.  Von-Mises stress predicted using FEM for a specimen with 2 mm hole.

DownLoad: Full-Size Img PowerPoint

Figure 13.  Von-Mises stress predicted using FEM for a specimen with 4 mm hole.

DownLoad: Full-Size Img PowerPoint

Figure 14.  Von-Mises stress predicted using FEM for a specimen with 6 mm hole.

DownLoad: Full-Size Img PowerPoint

Figure 15.  Von-Mises stress predicted using FEM for a specimen with 8 mm hole.

DownLoad: Full-Size Img PowerPoint

Figure 16.  Von-Mises stress predicted using FEM for a specimen with 10 mm hole.

DownLoad: Full-Size Img PowerPoint

Figure 17.  Von-Mises stress predicted using FEM for the specimen with 12 mm hole.

DownLoad: Full-Size Img PowerPoint

6.   Conclusion

Hybrid composite material such as copper/fiberglass composite laminates has a competitive role in Microelectromechanical systems (MEMS) in electrical and electronic applications. Modal analysis of free vibration for OH samples showed that their size effect in dynamic response has observed in the low modes 1, 2. Whereas, in larger modes, its effect is very little due to low stabilities. The increasing of the hole diameter in the plate gives a vibration relive greater than in case of static loading where a stress concentration problem is existing. The damping ratio logically decreases with increasing hole diameters as the hole deviates the vibration waves. On the other hand, finite element modeling revealed that all maximum Mises stresses are near fixation end while the minimum ones are located at the free end of the plate. Moreover, Mises stresses exhibit medium regions’ effect around the holes. Finally, it is reported that the cantilever beam boundary condition is suitable for the two modes in the case of hybrid composite material.

Conflicts of interests

The authors declare no conflict of interest.