Extension of SABR Libor Market Model to handle negative interest rates

1.   Introduction

Libor Market Model (LMM) has been the de facto standard term structure model^* for pricing (exotic) fixed income derivatives, as introduced in Brace (1997). Variations of LMM include normal, lognormal, shifted lognormal, and CEV LMMs, see Anderson and Andreason (2000). Recently stochastic volatility model, e.g., Stochastic Alpha-Beta-Rho (SABR) volatility, has been introduced into LMM framework to model volatility smile, see Joshi and Rebonato (2003); Rebonato (2007); Rebonato et al. (2009); Ferreiro et al. (2014).

^*Term structure models including LMM and Dynamic Nelson-Siegel Models (see Pedersen and Swanson (2019)) have inherent advantage over traditional short rate models.

SABR is a conceptually simple and flexible stochastic volatility model used to capture the volatility smile on caps/floors and swaptions. A drawback of the SABR model is that it only captures a single forward rate. On the other hand, LMM governs the evolution of the whole yield curve (or all forward rates). The classical LMM has no capability of matching the volatility smile on vanilla options.

The blend of the two industry standard models allows not only forward rates and forward rate stochastic volatilities to evolve under the same measure but also to describe correlations among forward rates and their volatilities. The proposed new model also allows volatility smiles.

In fact, various stochastic volatility extensions of LMM have been studied over the recent years. Shifted lognormal dynamics have been described in Joshi and Rebonato (2003); a Heston type dynamics have been studied in Piterbarg (2003) and Wu and Zhang (2006). See also Zhu (2007) for another interesting approach.

The SABR volatility dynamics have been studied in Henry-Labordere (2007); Morini and Mercurio (2007); Rebonato(2002, 2007). Most stochastic volatility LMMs introduced in the financial literature only allow one stochastic volatility factor to drive all forward rates. The dynamics proposed in HenryLabordere (2007) assume that there is a single stochastic volatility process which drives the volatility of each LIBOR forward. This assumption is motivated by considerations of mathematical tractability. López-Salas and Vázquez (2018) apply a sparse grid combination technique to compute derivative prices numerically under the SABR-LMM framework. In general, a parsimonious model (in terms of parameters and volatility structure) avoids over-parameterisation and ensures stability.

However, SABR process is defined only for positive (forward) rates (as the CEV parameter $\beta > 0$). In market conditions when rates are extremely low or even negative, it is important to extend the SABR model to negative rates^†. An intuitive extension of standard SABR to negative rates is Free-Boundary SABR (or FB-SABR, see Antonov et al. (2015)). In its stochastic PDE (SPDE) definition, forward rate is replaced by taking absolute value so as to allow rate to go below zero. The new rate dynamic is therefore

^†Negative rate policy has been adopted in many countries, such as Japan (see Honda and Inoue (2019)) and European countries including Sweden, Denmark, and Switzerland to spur economy growth.

The goal of this paper is to introduce FB-SABR into LMM to handle volatility smile under negative rate environments.

We call this new variant of LMM as FB-SABR-LMM. This new model can be used to price interest rate instruments with negative strikes as well as to recover implied volatility surface. The FB-SABR-LMM is structurally similar to the SABR-LMM. While FB-SABR replaces SABR in SPDE, other LMM features (such as time homogeneous volatility function, vol-vol function, and correlation matrix) remain the same. FB-SABR-LMM can be calibrated to ATM and OTM swaptions. We will compare FB-SABR-LMM with the standard SABR-LMM in later sections.

There are other variants of SABR model to handle negative rates. The simplest way is to shift the SABR process to the positive rate region. However, the choice of an appropriate shift size is a tricky setting. Alternatives include normal and mixture SABR, summarized in the following:

$1.$ Shifted SABR

where $s$ is a non-negative shift size chosen apriori.

$2.$ Normal SABR (see (May 2013)) corresponds to the case when CEV parameter $\beta = 0$, the Normal SABR model naturally handles negative interest rates.

$3.$ The mixture SABR assumes the forward rate is decomposed to two processes

where $F_t^{(1)}$ is a stochastic process following a zero-correlation SABR model and $F_t^{(2)}$ is a process following a normal SABR model. $\chi$ is a Bernoulli variable with a given success probability.

The three SABR extensions can all be used in the LMM construction, see Joshi and Rebonato (2003); Rebonato et al. (2009); Rebonato (2007).

The paper is organized as follows. In Section 2, we introduce notations and backgrounds. Standard LMM will be briefly introduced in Section 2.2; SABR and FB-SABR will be presented in Sections 2.3 and 2.4 subsequently. The structure of FB-SABR-LMM will be finally outlined in Section 3; model calibration will be outlined in Section 4. Section 5 includes an actual calibration example using interest rate swaptions. Conclusion of this study and future works will be collectively summarized in Section 6 of this paper.

2.   Preliminaries

2.1.   Notations and definitions

A tenor structure $(T_i)$, ${i\in\{0, 1, \ldots, N+1\}}$ is a set of discrete time points (i.e., tenor) that are often approximately equally spaced such that

where $\tau_i$ is the time fraction between adjacent tenors.

Next, consider a forward rate indexed by $i$ for $t < T_i$ denoted by $F_t^i$ as

which represents a forward rate which resets at time $T_i$ and matures at $T_{i+1}$.

Let $B_t^i : = B(t, T_i)$ the time $t$ price of a zero coupon bond that matures at time $T_i$. The forward rates can be written in terms of zero coupon bond price as follows:

In this paper, the calibration of FB-SABR-LMM will rely on market quotes of interest rate swaptions. Therefore we introduce relevant concepts and notions on swaption with the underlying swap herein. Authors realize that LMM can also be calibrated to interest rate caps and floors since their valuation is determined (in theory) by the same underlying rate as swaptions. However, discussions of caps and floors are not included in this paper.

Vanilla swaptions are European style options on swaps. A swap over a time horizon $[T_m, T_n]$ is a contract between the long and short parties. A swap exchanges cash flows tied to forward rates $F^i, i \in \{m, ..., n-1\}$ with a fixed rate of $K$ called strike, on some notional. In a payer (receiver) swap the long (short) pays the fixed rate $K$ in exchange of floating rate $F^i$.

The swap rate (or the par rate, the break-even rate) at time $t\leq T_m$ over the period $[T_m, T_n]$ is given by

where the swap numeraire is defined as

A rearrangement of terms shows that a swap rate can be written as a weighted sum of the forward rates:

where

is a slowly time-varying component. LMM directly models dynamics of forward rates $F_t^i$. This swap rate approximation formula (10) is a key formula in LMM to link swap rate with pieces of forward rates and is also used in deriving LMM implied swaption volatility (see Brigo and Mercurio (2006)).

The payoff of a swaption on a payer swap at time $T_m$ is given as

2.2.   Libor Market Model

Libor Market Model (LMM) has been the industry standard of modeling complicated interest rate derivatives. It allows joint evolving of all forward rates under one single measure. Hence the dynamics of the whole yield curve are captured. The model involves many parameters that allow the model to fit the whole time zero yield curve. The LMM has gained its popularity as the underlying forward rates are 'directly observable' from market.

The following discussion of LMM follows Anderson and Andreason (2000). Define the right continuous interval mapping function $\eta(t):[0, T_N) \to {1, ..., N}$ such that

The spot numeraire, or the continuous bank account numeraire, is expressed in terms of

Under spot measure, the LMM dynamics read:

where expectation is taken under spot measure; $W^i_t$ is Brownian motion under spot measure; $\rho_{jk}$ is correlation of forward rates $F_t^j$ and $F_t^k$; $\sigma_k(t, F^j_t)$ is an instantaneous (local) volatility function to be specified. Note that LMM dynamics can also be written under forward measure.

Correlation and volatility functions play a key role in LMM. The instantaneous correlation matrix in LMM can be estimated from historical forward rates, and it is called exogenous correlation. An additional adjustment step is often required to ensure positive semi-definity of the matrix. The positive semi-definite correlation matrix can further be rank-reduced and/or smoothed. On the other hand, parametric forms of correction increase model diversities to match market data.

The instantaneous volatility is a time homogeneous function and it has many forms (see Section 6.3.1 of Brigo and Mercurio (2006)), including variants of piecewise linear and 'humped' forms. The latter is common because of its simplicity.

It has been noted that the swap rate can be written as a weighted sum of the forward rates in Equation (10). In Rebonato's calibration formula for LMM the weights are fixed at time zero values. In normal, lognormal and CEV LMM, the implied swaption volatility approximation formula can be derived in the similar manner (see Chapter 6 of Brigo and Mercurio (2006)). For example, in the normal LMM, the Rebonato formula is:

where $w_i(0)$, $w_j(0)$ are the time zero weight of forward rates $F^i$ and $F^j$ (see Equation (10)).

Calibration is often done by minimizing the sum of squared error between the market and model implied volatility over all the calibration instruments:

2.3.   SABR

2.3.1.   SABR stochastic process

The SABR-LMM represents the recent development of LMM Rebonato et al. (2009). The core part of the SABR Libor Market Model is the underlying SABR type stochastic volatility process, see Hagan et al. (2002). For a forward rate $F_t$ (ignoring index $i$ for now),

where the rate process $F_t$ (starting with $F_0$) and the volatility process $\sigma_t$ are correlated $\langle \mathrm{d} Z_{t}, \mathrm{d}W_{t}\rangle = \rho \mathrm{d}t$. The SABR process is therefore defined by a four-parameter set $(\alpha, \nu, \beta, \rho)$, where $\alpha = \sigma_0$ is initial volatility, $\nu$ is volatility of volatility (vol-vol), $\beta$ is CEV parameter, and $\rho$ is correlation between the rate and volatility processes.

2.3.2.   Hagan formula and SABR calibration

SABR model can be efficiently calibrated using Hagan's implied volatility approximation formula, see Hagan et al. (2002). The Hagan formula directly approximates the lognormal volatility using the SABR parameters. Due to simplicity of the form, the Hagan formula facilitates fast SABR calibration to market volatility. The explicit form for the Hagan formula can be found in Hagan's original paper Hagan et al. (2002). Note that in order to use this approximation formula, one should have $F, K > 0$, where $F$ is ATM forward rate and $K$ is strike rate. Otherwise a displacement (or shift) is applied to both forward and strike (so that the difference of the two would not change), leading to an alternative model called displaced/shifted SABR.

These closed form formulas make it straightforward for SABR calibration to the market data.

SABR model might be over-parametrized. In order to stablize parameter estimates, $\beta$ is usually pre-determined. According to the relationship of $\sigma_{ATM}$ and ATM forward rate $F_{ATM}$ following

$\beta$ can generally be estimated using a linear regression of $\ln \sigma_{ATM}$ and $\ln F_{ATM}$. Other parameters are solved through the following optimization:

where $\sigma_N^{market}(K)$ is normal volatility observed from market. Besides, $\alpha$ can be associated with the ATM volatility and solved by a polynomial function (given other parameters) to further reduce the parameter degree of freedom.

2.4.   FB-SABR and negative rates

2.4.1.   FB-SABR stochastic process

In the negative interest rate setting, Antonov et al. (2015) propose the Free Boundary-SABR (FB-SABR) extension to the rate process:

for $0\leq \beta \leq \frac{1}{2}$. By introducing the absolute sign, the quantity $|F_t|^\beta$ is therefore defined for negative rate while the original $F_t^\beta$ is not. In this paper, we adopt the same idea of FB-SABR to extend the standard SABR-LMM to FB-SABR-LMM.

This section provides a short summary for the FB-SABR model. Readers can refer to Antonov et al. (2015) for additional details.

For model calibration, we use approximation formula for Bachelier volatility in Kienitz (2015), which follows essentially the same derivation process as the Hagan formula:

where $F$ is the ATM forward rate, the function $C(F) = |F|^{\beta}$ and further derivation shows that

Here $z = \frac{I}{\alpha}$, $\xi = \nu z$, $x(\xi) = \log\left(\frac{\sqrt{1-2\rho\xi + \xi^2}-\rho+\xi}{1-\rho}\right)$. Note that Kienitz (2015) also shows a benchmark comparison to the PDE solution using the Lawson-Swayne scheme, see LeFloch and Kennedy (2013).

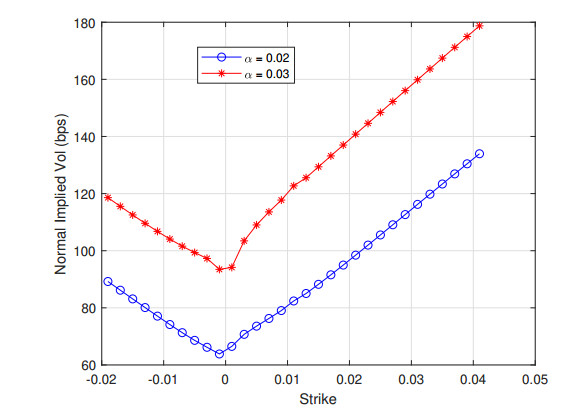
Figure 1 plots an example of implied volatility curve that crosses the zero boundary, using parameters: $\alpha = 0.02 \; (\text{and} \; 0.03)\; \nu = 0.5, \; \beta = 0.2, \; \rho = 0.3$ and $F_{ATM} = 0.01$. As shown in the figure, the implied volatility curve can be non-smooth around strike equal to 0.

2.4.2.   FB-SABR density

The terminal forward rate density in FB-SABR model can be analytically solved under appropriate boundary conditions, see Chesney et al. (2009). In the zero-correlation case when $\rho = 0$, Antonov et al. (2015) obtain an analytical form for the density function as a summation of a reflecting and an absorbing solution

where $p_R(t, |f|)$ and $p_A(t, |f|)$ stand for the reflecting density and absorbing density, respectively. However, for the general case when $\rho \neq 0$, the derived implied volatility function includes two level integrals.

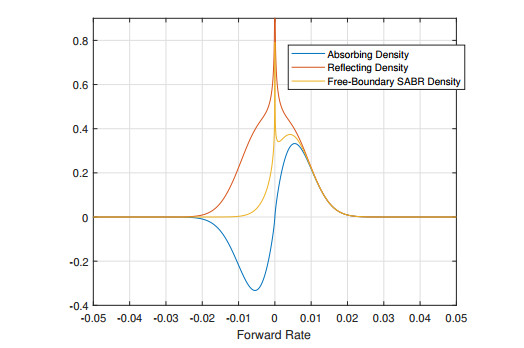
In case that the time zero forward rate of 50 bps that expires in 3 years, the terminal distribution of the forward rate densities (i.e., absorbing, reflecting and the average of the two) are depicted in Figure 2. Note that the model implied density around zero forward rate is spiky which contradicts the density function in reality. This is a FB-SABR model limitation and would cause unexpected model behavior around zero rate; while for rates away from zero, the spiky density issue is mitigated. One possible resolution is to smooth out the spike after FB-SABR model calibration (and normalization would be needed to make the smoothed function a legitimate density function). Besides, the negative absorbing density around zero is an artifact introduced by the model, however the average/sum of absorbing and reflection densities is positive.

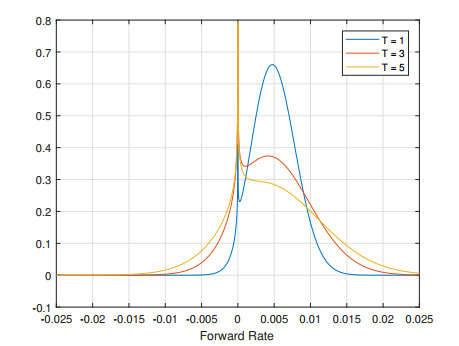
The evolution of terminal distribution with respect of time to expiry can be visualized in the following chart, for 1, 3 and 5Y in Figure 3.

Density of FB-SABR can go across zero. However, there is a spike around zero, and the spike tends to smooth out as it is approaching to expiry.

3.   FB-SABR-LMM

3.1.   FB-SABR-LMM stochastic process

Define the forward rate $F_t^{i}$ with resetting time $T_i$ and paying time $T_i + \tau$. Under the forward measure, the FB-SABR-LMM structure is

Comparing to the standard SABR-LMM, the only change is the term $|F_t^{i}|^{\beta^{i}}$ in Equation (27). For each single forward rate under corresponding forward measure, it follows SABR with CEV parameter $\beta^{i}$ which is usually the same constant for all $F_t^i$.

The correlations among forward rates and stochastic volatilities are characterized by $\rho_{i, j}, r_{i, j}$ and $R_{i, j}$ Define the correlation matrix $\boldsymbol{\rho} = \{\rho_{i, j}\}$, $\boldsymbol{r} = \{r_{i, j}\}$, and $\boldsymbol{R} = \{R_{i, j}\}$. The large correlation matrix $\boldsymbol{P}$ is:

Note that often the case the volatility function $g^T_t = g(T-t)$ is chosen to be a time homogeneous (invariant with different starting time) function. This simplifies model parametrization and calibration.

Besides, the volatility process $k_t^{i}$ is a lognormal process under the corresponding forward measure. The vol-vol function $h^T _t = h(T-t)$ is also a time homogeneous function. The functions $g$ and $h$ can be regarded as deterministic and stochastic volatility functions in SABR-LMM.

3.2.   FB-SABR-LMM under spot measure

It is desirable to calibrate (and simulate) all forward rates under a single measure. Common choices of measures include forward measure (e.g., terminal measure) and spot measure. In this paper, we use spot measure for being consistent with Rebonato's original approach, see Rebonato et al. (2009). The spot numeraire is defined in Section 2.2 of this paper. Applying the spot measure requires deriving the drift term of the rate dynamics.

Under spot measure, the FB-SABR-LMM dynamics can be written in the following form:

where $\sigma_t^j = g_t^jk_t^j$. Correlations are the same as specified in Equations (30) to (32).

Under such a formulation, all forward rates are brought under the same measure. The $g$ and $h$ functions that control the evolution of volatility are parametrized by time homogeneous functions for all forward rates and can be calibrated to market instruments efficiently.

3.3.   Model parametrization

The key component in building a FB-SABR-LMM is model parametrization. As it has been discussed in SABR model, the $\beta$ parameter is often determined apriori. In SABR- LMM, one single $\beta$ can be applied to all forward rates. It could come from the $\beta$ value that has been chosen in calibrating SABR models for individual forward rates.

Meanwhile, the volatilities (including the initial values) are governed by the $g$ and $h$ functions, and the correlations are specified in $\boldsymbol{P}$. These are key model parameters in applying FB-SABR-LMM.

3.3.1.   Volatility function

The volatility functions (i.e., $g$ and $h$) are chosen to be a four-parameter time homogeneous "humped" function of the following form :

Depending on the values of parameters, $g(\tau)$ and $h(\tau)$ can be a humped or monotonic function of $\tau$. The instantaneous volatility is: $\lim_{t \rightarrow 0}g(\tau) = \alpha_g + \delta_g$. Further, the terminal volatility is $\lim_{\tau \rightarrow \infty}g(\tau) = \delta_g$. The extrema is given at

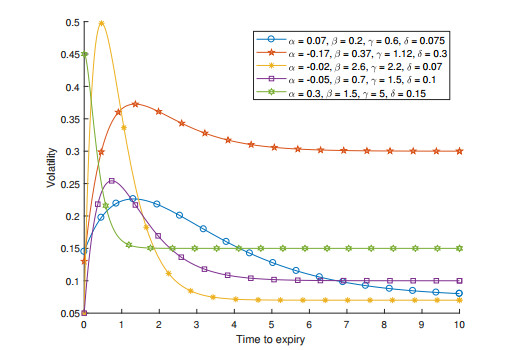
For very short and very long expiries, the volatility is usually lower. The most uncertainty in rates, and therefore the large value of volatility under normal market conditions is in the intermediate region (e.g., 6 to 18 months). In excited conditions, the lack of any consensus in decisions in monetary authorities (regarding to interest rates) will affect the earliest expiring forward rates, and hence the volatility for short expiries is high. Such that a monotonically decreasing volatility curve may be observed in the market. See Figure 4 for an illustration of different shapes of volatility functions.

Based on the value of the calibrated parameters, the function can either take humped shape, or monotonically decreasing shape. Notice that the hump functions are square integrable to allow closed form solutions for their integrals, which will be valuable when it comes to derive the model implied volatility approximation formula.

3.3.2.   Correlation matrix

The instantaneous correlation matrix in LMM can be estimated from historical forward rates, such that this is sometimes called exogenous correlation.

To use the raw historical correlation, pairwise Pearson correlation coefficients are plugged into the correlation matrix. In order to ensure positive semi-definite property, one can adjust the matrix; for example, by eliminating negative eigenvalues in the spectrum representation of the matrix.

The positive semi-definite correlation matrix is usually further rank-reduced and/or smoothed. In practice, a $p$-factor LMM is associated with a correlation matrix of rank $p$ (e.g., $p = 3$ as a common choice). For instance, a rank reduction can be performed on the adjusted historical correlation. Rank reduction methods include Principal Component, Discrete Cosine Transform, and Rebonato Angle Correlation (see Brigo and Mercurio (2006)).

Alternatively, one could calibrate a parametric correlation matrix within model calibration. The simplest form is an exponential function so that the off-diagonal entries diminishe to zero exponentially as a function of distance to the diagonal:

Other options can also be considered in the construction of the big correlation matrix $\boldsymbol{P}$. Note that in Section 2.3.1 we use $\rho$ to represent the correlation between rate and its volatility in the standard SARB model. However, in the context of FB-SABR-LMM, $\boldsymbol{\rho}$ represents the correlation matrix between forward rates.

The following discussion covers some common correlation parametrizations. The actual form implemented in this paper will be revisited in the forthcoming sections.

$1.$ The rate correlation matrix $\boldsymbol{\rho}$ follows the Lutz's 5 parameter form (i.e., $\alpha, \beta, \gamma, \delta, \rho_\infty$)

and

where

$2.$ The rate-volatility correlation matrix $\boldsymbol{R}$ (with parameters $\lambda_1$ and $\lambda_2$) takes the form of:

where $R_{ii}$ are the individual forward-volatility correlations and it can come from the calibrated SABR models for individual forward rates.

Another choice is simply a three-parameter (i.e., $R_0, a, c$) exponential function

$3.$ The volatility-volatility correlation matrix $\boldsymbol{r}$ can follow either exponential function, or two-parameter (i.e., $\gamma$ and $\eta$) SC form (Schoenmakers and Coeffey (2000)):

where $i$ and $j$ are row/column indexes and $N$ is the matrix dimension;

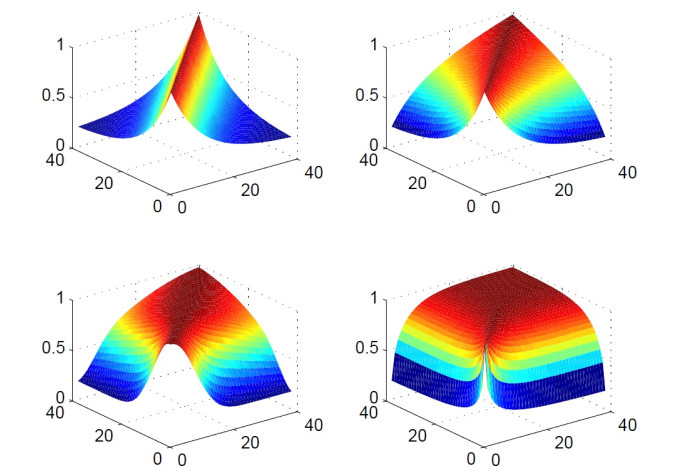
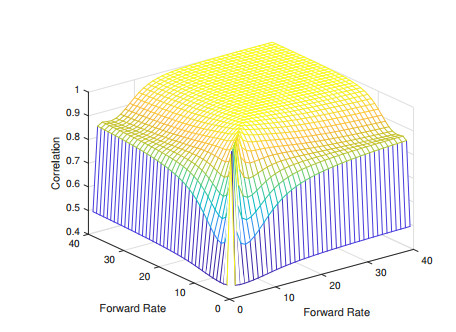
There are various parametric approaches to constructing correlation matrix. The reason we adopt the Lutz's 5-parameter form is because of its flexibility in generating different types of correlation matrices. The possible shapes of the 5-parameters Lutz's correlation are illustrated in Figure 5 (and SC form can generate similar shape of the correlation matrix depending on the values of the parameters). The parameters used in this example are tabulated in Table 1.

4.   FB-SABR-LMM calibration

The calibrations of SABR-LMM and its free boundary version are quite similar. We will present an actual calibration example to elaborate the process. The following table compares the two models, SABR-LMM and FB-SABR-LMM, side by side.

The first step of the calibration is to obtain the SABR parameters for forward rates of various tenors. Then these SABR parameters are used as market input for the calibration of functions $g$ and $h$, which control volatility structure of forward rates. The last step is the calibration of correlation among these forward rates, see Table 2. In Section 5 we provide a real calibration example following the steps.

4.1.   Step 1

SABR/FB-SABR parameters are used as market inputs in the calibration of SABR-LMM/FB-SABR-LMM model: 1) $\beta$ in SABR/FB-SABR will be used in the LMM; 2) other SABR/FB-SABR parameters are used in calibrating the volatility functions $g$ and $h$.

One could use caplets/floorlets in calibrating SABR/FB-SABR for each single forward rate process. Approximately, one could derive the parameters using swaption with small tenor (so as to approximate caplets/floorlets).

Calibration follows Hagan's paper by minimizing the squared difference between market volatilities and model implied volatilities. For the standard SABR parameters, it is the original Hagan formula or corresponding normal implied volatility formula. For FB-SABR parameters, it would be the normal implied volatility approximation formula Equation (24).

4.2.   Step 2

Next step is the calibration of volatility functions $g$ and $h$. One could use the caplet implied volatility or the implied volatility corresponding to the shortest tenor. The SABR parameters calibrated for each individual forward rate (in Step 1) play a central role of this step. Let

Besides, denote

interpreted as the deterministic volatility function associated with forward rate $F_t^i$; and

interpreted as the stochastic volatility function associated with forward rate $F_t^i$. The function $h_t^i$ is square integrable and the stochastic volatility $k^i$ is on average $k_0$ (as required). Therefore one could calibrate the function $g_t^i$ like in the standard LMM with deterministic volatility:

where

and $\epsilon_1$, $\epsilon_2$ are lower bounds for instantaneous and terminal volatilities.

The above optimization process calibrates the function to the deterministic volatility averaged over all forward rates. Approximately that

should be close to 1 if the fit of $\hat{g}^i$ is adequate.

In the subsequent calibration of function $h$, let's first define

and set up the optimization problem as

In addition if the fit of $h$ is adequate, the following correction term should be close to 1

4.3.   Step 3

The final step is the calibration of correlation structure, if correlation is not exogenous (e.g., historical correlation). Since swap rate is a "weighted average" of multiple forward rates, the calibration of correlation can be carried out by either swaps or swaptions.

In this paper, we discuss the approach of using swaptions. Assume that forward rates under spot measure follow FB-SABR-LMM dynamics, then the following discussion explains how to approximate a SABR process for swap rate (under swap measure). Note that we use the same $\beta$ parameter in swap rate process as in FB-SABR-LMM. Let $\Sigma_0$ be the initial swap rate volatility, $R_{SABR}$ the correlation between the swap rate and the volatility of the swap rate; $V$ the vol-vol of the swap rate.

Once functions $g$ and $h$ are calibrated, the swap rate SABR parameters can be expressed as a function of correlation matrix and therefore be calibrated to swaption volatility, same as standard SABR calibrated to a single swaption.

The approximation follows Rebonato's freezing technique, see Rebonato et al. (2009):

where

which is a slowly changing function of $t$ and can be fixed at the value of time zero (in case of FB-SABR when rates can be negative, absolute values are taken in the above formula); and

is the weight for a particular forward rate, and

is the CEV parameter for swap rate, as $\beta_k$ are all the same, we have that $B$ equals the CEV parameter $\beta$ in SABR.

Besides, the SABR correlation parameter between swap rate and its volatility, $R_{SABR}$, can be approximated by the following:

where

Given SABR parameters for swap rate, the correlation parameters (which are the only unknown) are calibrated to swaption volatility by the Hagan formula, as ordinal SABR model for swaptions.

Next, we will examine an actual example to streamline the model calibration process.

5.   An actual model calibration example

In the previous section we outline FB-SABR-LMM calibration steps. In this section, actual model calibration steps are outlined with results on the date August 1, 2017. The instruments of calibration are interest rate swaptions. All implementation is programmed in MATLAB based on a computer with Intel i7-8700 CPU. The calibration of the functions $g$ and $h$ and the correlation matrix $\boldsymbol{P}$ takes less than 10 minutes to complete.

5.1.   Step 1 - Calibrate FB-SABR parameters

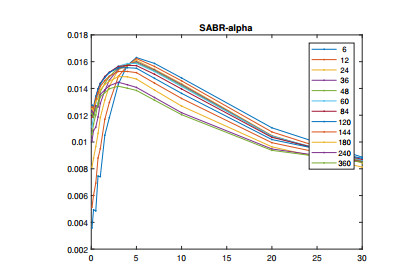
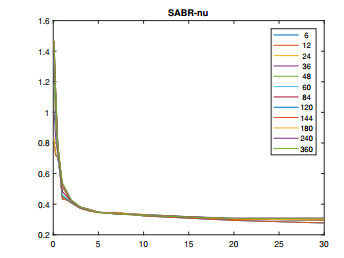
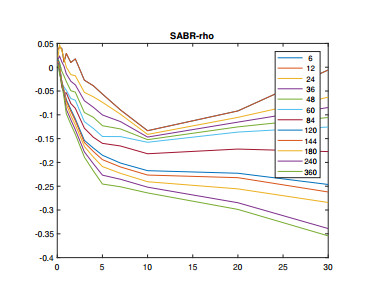
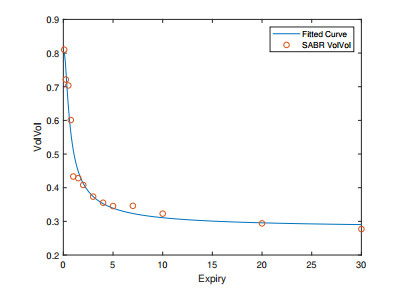
Note that the FB-SABR parameters are calibrated (for different expiry-tenor combinations) prior to the calibration of FB-SABR-LMM. The FB-SABR parameters are "market input" for the LMM counterpart. In this calibration exercise, we fix $\beta = 0.2$ for all SABR forward rates. Calibrated $\alpha, \nu, \rho$ are depicted in Figures 6, 7 and 8. While different curves are corresponding to tenors, a single curve is a function of swaption expiry (x-axis).

Our FB-SABR-LMM is constructed using a base tenor of 6M. As 6M expiry swaption implied volatilities are not available, we extrapolate the expiry curve and use it for calibrating the volatility function $g$, which critically determines the level of volatilities. The cap or floor (embedding 6M tenor caplets or floorlets) implied volatilities are generally consistent with 6M expiry swaption implied volatilities; however, in our experiment calibration based on 6M expiry swaption volatilities yields a more stable function $g$ and less deviance with longer maturity swaption volatilities. We believe this extrapolation approach is better than directly using caplet implied volatilities.

5.2.   Step 2 - Calibrate volatility function and vol-vol function

The volatility function is associated with $g$ and $h$ functions. Both functions are parametrized by a 4-parameter "humped" function. By calibrating to 6M-expiry swaption with various tenors, the two functions take either humped shape, or monotonically decreasing shape, shown below. The parameter estimates are summarized in Figures 9 and 10.

5.3.   Step 3 - Calibrate correlation matrix

Each of the blocks of the big correlation matrix P can be parametrized. For example, $\boldsymbol{\rho}$ matrix is parametrized by Lutz's 5 parameter form. We use swaptions with expires in {6M, 1Y, 2Y, 5Y and 10Y}, and tenors in {6M, 1Y, 2Y, 5Y, 10Y, 20Y, 30Y}. Both ATM and OTM ($\pm 300$ bps when available) market swaption implied volatilities are included in the calibration. The calibrated $\boldsymbol{\rho}$ matrix is illustrated in Figure 11.

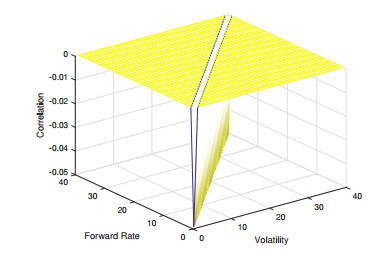
Meanwhile, for $\boldsymbol{R}$ and $\boldsymbol{r}$, we decide to use pre-determined form for simplicity. The $\boldsymbol{R}$ matrix takes the following form:

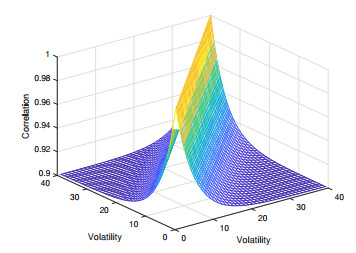
Matrix $\boldsymbol{r}$ takes the form of Doust correlation:

where $\beta = 0.2$ and $r_\infty = 0.9$. Plots of the matrices $\boldsymbol{R}$ and $\boldsymbol{r}$ are shown in Figures 12 and 13.

5.4.   Swaption implied volatility and price

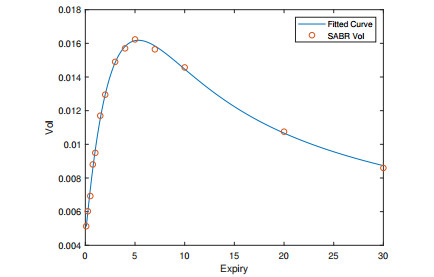
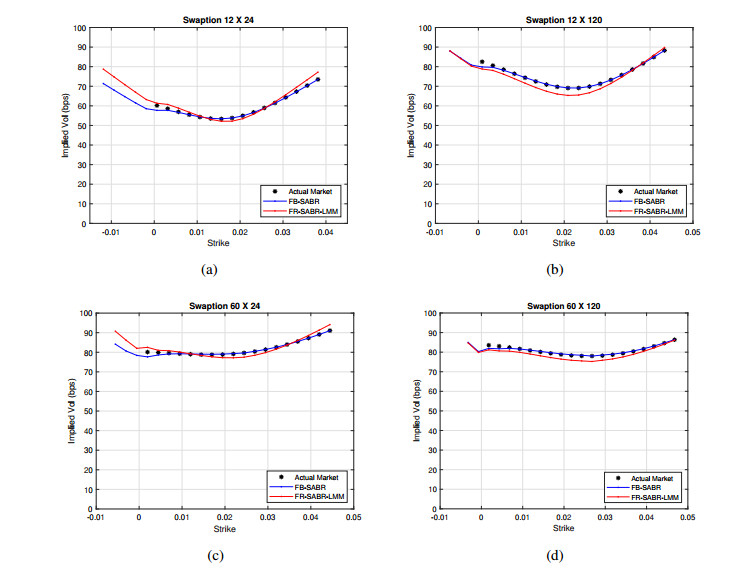
The FB-SABR-LMM's main parameters are the calibrated volatility functions $g$ and $h$, and the correlation matrix $\boldsymbol{P}$. For each swaption instrument, the model yields a set of reconstructed FB-SABR parameters that determine the volatility smile curve. As examples, the calibrated implied volatility smiles for various swaption instruments are shown in Figure 14. These sample swaptions are 12Mx24M (or 1Yx2Y or simply noted as 12x24), 12x120, 60x24 and 60x120 swaptions. As shown in the figure, the FB-SABR structure by simply fitting the market implied volatility matches the source data closely. The volatility smile naturally extends to the negative strike range.

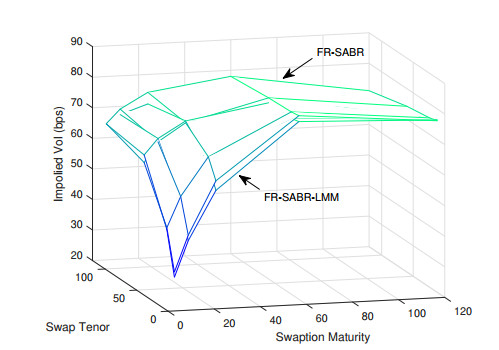
Figure 15 plots the reconstructed ATM implied volatility surface. The volatility surface is based on a combination of maturity values and tenor values: Maturity set = {6, 12, 24, 60,120} and Tenor set = {12, 24, 60,120}.

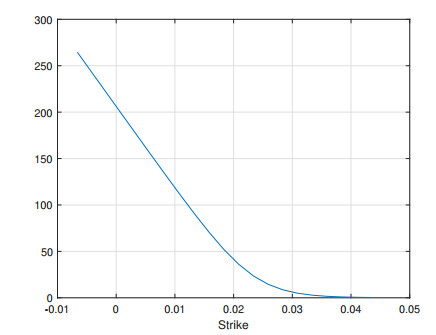
More analysis results are present here using the 12x120 swaption as an example. The FB-SABR-LMM yields a set of FB-SABR parameters that are close to the source FB-SABR parameters, see Table 3. The corresponding payer swaption prices across negative positive strikes (＄1,000 notional) are shown in Figure 16.

6.   Conclusion

FB-SABR is a natural extension of standard SABR to model negative rates. LMM with stochastic volatility is an extension of standard LMM to incorporate market volatility "smile". The combination of FB-SABR volatility with LMM brings volatility smile into LMM that also allows negative rates. This leads to a new LMM variant FB-SABR-LMM covered in the paper.

We introduced structure and calibration of FB-SABR-LMM. Its main structure shares the major components in standard SABR-LMM with one difference which is the use of FB-SABR as the base dynamics for forward rates. The implied volatility is therefore normal implied volatility derived similarly as the Hagan formula. FB-SABR-LMM has a flexible structure allowing it to be calibrated to market instruments including swaptions. The correlation matrices are a key component in the calibration process, can either be exogenous or embedded in the model calibration. The FB-SABR-LMM naturally extends to the implied volatility surface to the negative rate region which addresses the conventional limitation that the zero boundary is an absorbing state as forward rate hits the zero boundary. The generated density function of the forward rate contains a kink at the zero rate region, but in general practice it does not affect our model construction.

We calibrated the volatility functions $g$ and $h$ following Rebonato's original method in SABR-LMM. Future works include exploring alternative functional forms of the functions $g$ and $h$, and calibrate simultaneously the functions $g$, $h$ and the correlation matrix $\boldsymbol{P}$ so that a more flexible and consistent model structure can be obtained.

Disclaimer

The opinions in this paper are strictly those of the authors and do not represent the views of Wells Fargo & Company, or any of their subsidiaries or affiliates.

Conflict of interest

The authors declare no conflict of interest.