In deep space exploration, the libration points (especially L2 point) of solar-earth system is a re-search hotspot in recent years. Space station and telescope can be arranged at this point, and it does not need too much kinetic energy. Therefore, it is of great significance to arrange flight formation on the libration point of solar-earth for scientific research. However, the flight keeping control technology of flight formation on the solar-earth libration points (also called Lagrange points) is one of the key problems to be solved urgently. Based on the nonlinear dynamic model of formation flying, the improved successive approximation algorithm is used to achieve formation keeping con-trol. Compared with the control algorithm based on orbital elements, this control algorithm has the advantages of high control accuracy and short control time in formation keeping control of solar-earth libration points. The disadvantage is that the calculation is complicated. But, with the devel-opment of computer technology, the computational load is gradually increasing, and there will be more extensive application value in the future. Finally, the error and control simulations of the formation flying of the spacecraft with the libration points of the solar-earth system are carried out for two days. The simulation results show that the method can quickly achieve the requirements of high-precision control.
Citation: Zhenqi He, Lu Yao. Improved successive approximation control for formation flying at libration points of solar-earth system[J]. Mathematical Biosciences and Engineering, 2021, 18(4): 4084-4100. doi: 10.3934/mbe.2021205
In deep space exploration, the libration points (especially L2 point) of solar-earth system is a re-search hotspot in recent years. Space station and telescope can be arranged at this point, and it does not need too much kinetic energy. Therefore, it is of great significance to arrange flight formation on the libration point of solar-earth for scientific research. However, the flight keeping control technology of flight formation on the solar-earth libration points (also called Lagrange points) is one of the key problems to be solved urgently. Based on the nonlinear dynamic model of formation flying, the improved successive approximation algorithm is used to achieve formation keeping con-trol. Compared with the control algorithm based on orbital elements, this control algorithm has the advantages of high control accuracy and short control time in formation keeping control of solar-earth libration points. The disadvantage is that the calculation is complicated. But, with the devel-opment of computer technology, the computational load is gradually increasing, and there will be more extensive application value in the future. Finally, the error and control simulations of the formation flying of the spacecraft with the libration points of the solar-earth system are carried out for two days. The simulation results show that the method can quickly achieve the requirements of high-precision control.
Since the ISEE-3 mission launched in 1978, the detection of translation points has never been interrupted. In the past 30 years, five spacecrafts have been launched, but these spacecrafts are single-satellite missions. Due to the constraints of a single spacecraft (weight, size, fuel, etc.), it is impossible to complete large baseline length or large aperture astronomical observation with high resolution. With the rapid development of small spacecraft in recent years, many spacecrafts work together to complete formation flying tasks, which provides a feasible way to complete high-performance and high-resolution astronomical observation tasks. At present, the international space agency has attached great importance to the formation astronomical observation tasks, such as XUES, MAXIM, SI and Darwin [1,2,3].
The deployment of spacecraft formation in translational orbit can achieve interferometry of medium and long baseline, which is of great significance to the study of the origin of the universe. Firstly, the design of formation configuration and the formation preservation based on it are in-volved in the formation of translational spacecraft, and the formation preservation is one of the main difficulties. At present, Hamilton and Folta applied linear Optimal control technology to study formation control near Lissajous orbit in the real ephemeris model. Penin proposed offline planning and online adjustment algorithm for configuration reconstruction of deep space interfer-ometric formation [5]. Peng Haijun and Jiang Xin proposed a nonlinear control method for Space-craft Formation Reconfiguration in libration point orbit based on symplectic numerical algo-rithm [6,7,8,9]. Chai Runqi, Tsourdos Antonios et al work explores the optimal flight of aero-assisted reentry vehicles during the atmospheric entry flight phase with the consideration of both determin-istic and control chance constraints [10,11].
At present, most of the studies have not touched the vicinity of the solar-earth libration points. In this study, the improved successive approximation control method is used to maintain the for-mation flying control at the solar-earth libration points. Compared with the previous control meth-ods (such as LQR control method, SDRE control method, invariant popular control method, etc.), this method can further improve the accuracy of formation flight hold control, but the amount of calculation is large. It is suitable for long-term deep space exploration missions with high for-mation flying. At the same time, with the development of computer science, the computing power will also be enhanced. It is believed that the successive approximation method will get more atten-tion in the field of formation flight maintenance control in the future.
Because the dynamic large-scale system has the characteristics of "large scale, complex struc-ture, many factors and function synthesis", the analysis of large-scale system with conventional control theory and method can't achieve good control effect. Aiming at the general nonlinear inter-connected coupled large-scale system and a class of affine nonlinear similar composite large-scale system, a successive approximation method of Optimal control law design is proposed, Firstly, by using this method, the solution of high-order coupled nonlinear two-point boundary value problems is simplified to a series of decoupled linear two-point boundary value problems, and then it is proved that the solutions of the linear two-point boundary value problems uniformly converge to the Optimal control of nonlinear interconnected dynamic large-scale systems.
The successive approximation method is the simplest and systematic method to study the problem of non-linear local analysis based on the solvability of operator equation. The basic idea of this method is: For a given, displayed a Cauchy sequence of defined ele-ments, so that.
Based on the successive approximation method for local analysis of non-linear functions, an approximation method for solving the Optimal control problem of non-linear systems is proposed in reference [12]. First, the non-linear term in the system is treated as an external additional dis-turbance to the system. Then, according to the successive approximation method in differential equation theory, the non-linear two-point boundary value problem is transformed into a series of linear non-homogeneous two-point boundary value problems.
Considering Affine Nonlinear Systems
| $ \dot{x}\left(t\right) = Ax\left(t\right)+Bu\left(t\right)+f\left(x\right), t < 0 $ | (1) |
where:
| $ f\left(x\right) = G\left(x\right)x\left(t\right) $ | (2) |
Its cost function is:
| $ J = \frac{1}{2}{x}^{T}\left({t}_{f}\right){Q}_{f}x\left({t}_{f}\right)+\frac{1}{2}{\int }_{0}^{{t}_{f}}\left[{x}^{T}\right(t\left)Qx\right(t)+{u}^{T}(t\left)Ru\right(t\left)\right]dt $ | (3) |
Where: $ {Q}_{f} $ and $ Q $ are the weight matrix, R is the error matrix, $ {Q}_{f} $ and $ Q $ are the semi-positive definite constant matrix, R is the positive definite constant matrix.
According to Optimal control theory, the necessary conditions for this Optimal control problem are the boundary value problems of the following two points:
| $ \dot{x}\left(t\right) = Ax\left(t\right)-\lambda \left(t\right)+G\left(x\right)x $ | (4) |
| $ -\lambda \left(t\right) = Qx\left(t\right) = {A}^{T}\lambda \left(t\right)+F\left(x\right)\lambda \left(t\right) $ | (5) |
| $ \lambda \left({t}_{f}\right) = {Q}_{f}x\left({t}_{f}\right) , {x}_{0} = x\left(0\right) $ | (6) |
where: $ S = B{R}^{-1}{B}^{T} $, $ F\left(x\right) = \frac{\partial {f}^{T}\left(x\right)}{\partial x} $. The Optimal control law can be described by the following formula:
| $ {u}^{*}\left(t\right) = -{R}^{-1}{B}^{T}\lambda \left(t\right) $ | (7) |
Among them, the cost function $ J $ is mainly used to find the objective function of the optimal solution. If we want to find the optimal solution of Eq (1), that is to say, that is to say, we need to minimize the value of $ J $. The function of optimal control rate is to describe the functional relationship between controlled state variables and system input signals.
Construct the following sequence of two-point boundary value problems.
| $ \left\{\begin{array}{c}{x}^{\left(0\right)}\left(t\right) = 0\\ {\dot{x}}^{\left(k\right)}\left(t\right) = A{x}^{\left(k\right)}\left(t\right)-S{\lambda }^{\left(k\right)}\left(t\right)+G\left({x}^{(k-1)}\right){x}^{\left(k\right)}\left(t\right)\\ -{\dot{\lambda }}^{\left(k\right)}\left(t\right) = Q{x}^{\left(k\right)}\left(t\right)+{A}^{T}{\lambda }^{\left(k\right)}\left(t\right)+F\left({x}^{(k-1)}\right){\lambda }^{\left(k\right)}\left(t\right)\\ {\lambda }^{\left(k\right)}\left({t}_{f}\right) = {Q}_{f}{x}^{\left(k\right)}\left({t}_{f}\right)\\ {x}^{\left(k\right)}\left(0\right) = {x}_{0}\end{array}\right. $ | (8) |
where: $ 0 < t\le {t}_{f} $, $ k = \mathrm{1, 2}, 3\cdots $.
Definition: $ {G}^{\left(k\right)}\left(t\right) = G\left({x}^{\left(k\right)}\right) $
| $ {F}^{\left(k\right)}\left(t\right) = F\left({x}^{\left(k\right)}\right) ~~k = \mathrm{0, 1}, 2, \cdots $ | (9) |
The Eq (8) is a linear homogeneous two-boundary value problem, and its endpoint condition is also linear. It is known that the relationship between $ {\lambda }^{\left(1\right)}\left(t\right) $ and $ {x}^{\left(1\right)}\left(t\right) $ must be linear.
| $ {\lambda }^{\left(k\right)}\left(t\right) = {P}^{\left(k\right)}\left(t\right)*{x}^{\left(k\right)}\left(t\right) $ | (10) |
By deriving t on both sides of equation (10) and by the first and second equations in equation group (8), we can obtain:
| $ {\dot{\lambda }}^{\left(k\right)}\left(t\right) = [-Q-[{A}^{T}+{F}^{(k-1)}\left(t\right)\left]{P}^{\left(k\right)}\right(t\left)\right]{x}^{\left(k\right)}\left(t\right) $ | (11) |
Considering that $ {x}^{\left(1\right)}\left(t\right)\equiv 0 $ is not valid, Then the matrix differential equation satisfied by $ {P}^{\left(1\right)}\left(t\right) $ can be obtained as follows:
| $ {\dot{P}}^{\left(k\right)}\left(t\right)+{P}^{\left(k\right)}\left(t\right)[A+{G}^{(k-1)}(t\left)\right]\\ +[{A}^{T}+{F}^{(k-1)}(t\left)\right]{P}^{\left(k\right)}\left(t\right)-{P}^{\left(k\right)}\left(t\right)S{P}^{\left(k\right)}\left(t\right)+Q = 0 $ | (12) |
By using the endpoint condition, we can deduce that $ {P}^{\left(k\right)}\left(t\right) $ satisfies the following conditions:
| $ {P}^{\left(k\right)}\left({t}_{f}\right) = {Q}_{f} $ | (13) |
The corresponding Optimal control sequence is:
| $ {u}^{\left(k\right)}\left(t\right) = -{R}^{-1}{B}^{T}{\lambda }^{\left(k\right)}\left(t\right) $ | (14) |
The closed-loop system sequence of affine nonlinear systems is constructed as follows:
| $ \left\{\begin{array}{c}{\dot{x}}^{\left(k\right)}\left(t\right) = A{x}^{\left(k\right)}\left(t\right)-S{\lambda }^{\left(k\right)}\left(t\right)+G\left({x}^{(k-1)}\right){x}^{\left(k\right)}\left(t\right), \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}t > 0\\ {x}^{\left(k\right)}\left(0\right) = {x}_{0}, \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}k = \mathrm{1, 2}, 3\cdots \end{array}\right. $ | (15) |
Algorithm 1 Improved successive approximation algorithm for Optimal control approximation design of affine nonlinear systems
Step 1: Given the normal number $ \varepsilon $. Let $ k = 1 $, $ N = 1 $, from Eq (8), we can see that $ {x}^{\left(0\right)}\left(t\right) = 0 $. According to definition (9), $ {G}^{\left(0\right)}\left(t\right) $ and $ {F}^{\left(0\right)}\left(t\right) $ can be obtained.
Step 2: $ {P}^{\left(1\right)}\left(t\right) $ can be obtained from matrix differential equation (12) and its endpoint condition (13). Then, $ {u}^{\left(1\right)}\left(t\right) $ can be obtained from Eq (14). According to Eq (9), $ {G}^{\left(1\right)}\left(t\right) $ and $ {F}^{\left(1\right)}\left(t\right) $ are obtained. Substituting $ {x}^{\left(1\right)}\left(t\right) $ and $ {u}^{\left(1\right)}\left(t\right) $ into cost function (3) to calculate $ {J}^{\left(1\right)} $. Then, let $ k = 2 $;
Step 3: Matrix $ {P}^{\left(k\right)}\left(t\right) $ is obtained by matrix differential equation (12) and its endpoint condition (13). Then, $ {u}^{\left(k\right)}\left(t\right) $ is obtained from (14). $ {x}^{\left(k\right)}\left(t\right) $ is obtained from (15).
Step 4: Substituting $ {u}^{\left(k\right)}\left(t\right) $ and $ {x}^{\left(k\right)}\left(t\right) $ into cost function (3) to obtain $ {J}^{\left(k\right)} $, and the convergence index $ {J}_{e}^{\left(k\right)} $ of performance index $ {J}^{\left(k\right)} $ is calculated according to Eq (16).
| $ {J}_{e}^{\left(k\right)} = \frac{{J}^{\left(k\right)}-{J}^{(k-1)}}{{J}^{\left(k\right)}} $ | (16) |
Step 5: If $ \left|{J}_{e}^{\left(k\right)}\right| < \varepsilon $, let $ N = k $, then output is $ {u}_{N}\left(t\right) $; Now termination.
Step 6: $ {G}^{\left(k\right)}\left(t\right) $ and $ {F}^{\left(k\right)}\left(t\right) $ can be calculated from definition (9). Let $ k = k+1 $, then go to step 3.
Firstly, the following radiation nonlinear systems are considered.
| $ \left\{\begin{array}{c}\dot{x}\left(t\right) = A\left(x\right)x\left(t\right)+G\left(x\right)x\left(t\right), \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}t > 0\\ x\left(0\right) = {x}_{0}\end{array}\right. $ | (17) |
Where: $ f\left(x\right) = G\left(x\right)x\left(t\right) $, $ x\in {\mathbb{R}}^{n} $ is the state vector of the system, $ u\in {\mathbb{R}}^{n} $ is the control vector of the system, $ A\left(t\right) $ is a time-varying matrix of suitable dimension, $ {x}_{0} $ is the initial state vector of the state vector $ x\left(t\right) $.
Assuming that $ {t}_{f} $ is the terminal time of the system and based on the improved successive approximation method, the sequence of state equations for the two-point boundary value problem is:
| $ \left\{\begin{array}{c}{\dot{x}}^{\left(k\right)}\left(t\right) = A\left(x\right){x}^{\left(k\right)}\left(t\right)+G\left({x}^{(k-1)}\right){x}^{\left(k\right)}\left(t\right), \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em} < t < {t}_{f}\\ {x}^{\left(k\right)}\left(0\right) = {x}_{0}, \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}k = \mathrm{1, 2}\cdots \end{array}\right. $ | (18) |
The vectors sequence of Eq (13) is defined as follows:
| $ \left\{\begin{array}{c}{x}^{\left(1\right)}\left(t\right) = \varPhi (t, 0){x}_{0}\\ {x}^{\left(k\right)}\left(t\right) = \varPhi (t, 0){x}_{0}+{\int }_{0}^{t}\left[\varPhi \right(t, r\left)G\right({x}^{(k-1)}\left(r\right)\left){x}^{\left(k\right)}\right(r\left)\right]dr\\ {x}^{\left(k\right)}\left(0\right) = {x}_{0}, \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}k = \mathrm{1, 2}\cdots \end{array}\right. $ | (19) |
Where: $ \varPhi (t, 0) $ is the state transition matrix for $ A\left(t\right) $.
Since $ G\left(x\right) $ is Lipschitz on $ {\mathbb{R}}^{n} $, for any $ {x}^{\left(i\right)}, {x}^{\left(j\right)}\in U $, there is:
| $ \left\{\begin{array}{c}‖G\left({x}^{\left(i\right)}\right)‖\le \alpha ‖{x}^{\left(i\right)}‖\\ ‖G\left({x}^{\left(i\right)}\right)-G\left({x}^{\left(j\right)}\right)‖\le \alpha ‖{x}^{\left(i\right)}-{x}^{\left(j\right)}‖\end{array}\right. $ | (20) |
The Lipschitz constant of $ f\left(x\right) $ is assumed to be $ \beta $.
| $ \left\{\begin{array}{c}M = \underset{0\le t\le {t}_{f}}{sup}‖\varPhi (t, 0)‖\\ \gamma = \mathit{max}\left\{\underset{0\le t\le {t}_{f}}{sup}‖{x}^{\left(k\right)}‖, k = \mathrm{1, 2}, \cdots \right\}\end{array}\right. $ | (21) |
Where: $ M $, $ \gamma $ is a positive constant. $ ‖\varPhi \left(\mathrm{0, 0}\right)‖ = ‖I‖ = 1 $, the moral is that, $ M\ge 1 $.
Next, we prove that $ \left\{{x}^{\left(k\right)}\right(t\left)\right\} $ and $ \left\{{u}^{\left(k\right)}\right(t\left)\right\} $ respectively, converge uniformly to the optimal state trajectories $ {x}^{*}\left(t\right) $ and $ {u}^{*}\left(t\right) $ of the system (8) for quadratic performance indices.
The following lemma needs to be proved first.
Lemma 1 Assume that a and B are sufficiently small and satisfy $ M\alpha \gamma {t}_{f} < 1 $, $ \beta {t}_{f} < 1 $.
Then:
1) the system (8) has a unique solution in interval $ [0, {t}_{f}] $;
2) Sequence $ \left\{{x}^{\left(k\right)}\right(t\left)\right\} $ is the only solution that converges uniformly to the system (8).
Prove: (1) If $ f\left(x\right) $ is Lipschitz on $ {\mathbb{R}}^{n} $, and $ \beta {t}_{f} < 1 $, then the affine system (8) has a unique solution in interval $ [0, {t}_{f}] $.
(2) Consider $ \left\{{x}^{\left(k\right)}\left(t\right)\right\} $ as a sequence on $ {C}^{N}[0, {t}_{f}] $. From Eq (14) the following equation can be obtained.
| $ {x}^{\left(2\right)}\left(t\right)-{x}^{\left(1\right)}\left(t\right) = {\int }_{{t}_{0}}^{t}\left[\varPhi \right(t, r\left)G\right({x}^{\left(1\right)}\left(r\right)\left){x}^{\left(2\right)}\right(r\left)\right]dr $ | (22) |
Then,
| $ ‖{x}^{\left(2\right)}\left(t\right)-{x}^{\left(1\right)}\left(t\right)‖\le M\alpha {\int }_{{t}_{0}}^{t}\left(‖{x}^{\left(1\right)}\left(r\right)‖‖{x}^{\left(2\right)}\left(r\right)‖\right)dr $ | (23) |
For the same reason, the following equation can be obtained.
| $ {x}^{\left(3\right)}\left(t\right)-{x}^{\left(2\right)}\left(t\right) \\ = {\int }_{{t}_{0}}^{t}\left[\varPhi \right(t, r\left)\right(G\left({x}^{\left(2\right)}\right(r\left)\right){x}^{\left(3\right)}\left(r\right)-G\left({x}^{\left(1\right)}\right(r\left)\right){x}^{\left(2\right)}\left(r\right)\left)\right]dr $ | (24) |
According to Eq (15), the following equation can be obtained.
| $ ‖{x}^{\left(3\right)}\left(t\right)-{x}^{\left(2\right)}\left(t\right)‖ = M{\int }_{{t}_{0}}^{t}\left(‖G\left({x}^{\left(2\right)}\right(r\left)\right){x}^{\left(3\right)}\left(r\right)-G\left({x}^{\left(1\right)}\right(r\left)\right){x}^{\left(2\right)}\left(r\right)‖\right)dr \\= M{\int }_{{t}_{0}}^{t}\left[‖\left(G\left({x}^{\left(2\right)}\right(r\left)\right)-G\left({x}^{\left(1\right)}\right(r\left)\right)\right){x}^{\left(3\right)}\left(r\right)+G\left({x}^{\left(1\right)}\right(r\left)\right)\left({x}^{\left(3\right)}\left(r\right)-{x}^{\left(2\right)}\left(r\right)\right)‖\right]dr \\ \le M{\int }_{{t}_{0}}^{t}\left[\alpha ‖{x}^{\left(2\right)}\left(t\right)-{x}^{\left(1\right)}\left(t\right)‖‖{x}^{\left(3\right)}\left(r\right)‖+\alpha ‖{x}^{\left(1\right)}\left(t\right)‖‖{x}^{\left(3\right)}\left(r\right)-{x}^{\left(2\right)}\left(r\right)‖\right]dr \\ = M\alpha t‖{x}^{\left(1\right)}\left(t\right)‖‖{x}^{\left(3\right)}\left(r\right)-{x}^{\left(2\right)}\left(r\right)‖+M\alpha ‖{x}^{\left(3\right)}\left(r\right)‖{\int }_{{t}_{0}}^{t}\left(‖{x}^{\left(2\right)}\left(t\right)-{x}^{\left(1\right)}\left(t\right)‖\right)dr $ | (25) |
According to hypothetical conditions, the following equation can be obtained.
| $ ‖{x}^{\left(3\right)}\left(t\right)-{x}^{\left(2\right)}\left(t\right)‖\le \frac{M\alpha ‖{x}^{\left(3\right)}\left(r\right)‖}{1-M\alpha t‖{x}^{\left(1\right)}\left(t\right)‖}{\int }_{{t}_{0}}^{t}\left(‖{x}^{\left(2\right)}\left(t\right)-{x}^{\left(1\right)}\left(t\right)‖\right)dr $ | (26) |
Using Mathematical Induction, the following equation can be obtained.
| $ ‖{x}^{(k+1)}\left(t\right)-{x}^{\left(k\right)}\left(t\right)‖\le \frac{M\alpha ‖{x}^{(k+1)}\left(r\right)‖}{1-M\alpha t‖{x}^{(k-1)}\left(t\right)‖}{\int }_{{t}_{0}}^{t}\left(‖{x}^{\left(k\right)}\left(t\right)-{x}^{(k-1)}\left(t\right)‖\right)dr\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \\ \vdots \\ \hspace{0.33em}\le \frac{{M}^{k}{\alpha }^{k}{t}^{k}‖{x}^{\left(1\right)}\left(r\right)‖‖{x}^{\left(2\right)}\left(r\right)‖\cdots ‖{x}^{\left(k\right)}\left(r\right)‖}{k!\left(1-M\alpha t‖{x}^{\left(1\right)}\left(t\right)‖\right)\left(1-M\alpha t‖{x}^{\left(2\right)}\left(t\right)‖\right)\cdots \left(1-M\alpha t‖{x}^{(k-1)}\left(t\right)‖\right)} $ | (27) |
As Eq (16) is known, the right side of the inequality is enlarged.
| $ ‖{x}^{(k+1)}\left(t\right)-{x}^{\left(k\right)}\left(t\right)‖\hspace{0.33em}\le \frac{{M}^{k}{\alpha }^{k}{\gamma }^{k+1}{t}_{f}^{k}}{k!{\left(1-M\alpha \gamma {t}_{f}\right)}^{k-1}} $ | (28) |
According to the trigonometric inequality, for any number j, the following equation can be obtained.
| $ ‖{x}^{(k+j)}\left(t\right)-{x}^{\left(k\right)}\left(t\right)‖\le \sum \limits_{i = k+1}^{k+j}\frac{{M}^{i}{\alpha }^{i}{\gamma }^{i+1}{t}_{f}^{i}}{i!{\left(1-M\alpha \gamma {t}_{f}\right)}^{i-1}}\hspace{0.33em}\\ \le \frac{{M}^{k+1}{\alpha }^{k+1}{\gamma }^{k+2}{t}_{f}^{k+1}}{(k+1)!{\left(1-M\alpha \gamma {t}_{f}\right)}^{k}}\mathit{exp}\left(\frac{M\alpha \gamma {t}_{f}}{1-M\alpha \gamma {t}_{f}}\right) $ | (29) |
When $ k\to \infty $, $ \frac{{M}^{k+1}{\alpha }^{k+1}{\gamma }^{k+2}{t}_{f}^{k+1}}{(k+1)!{\left(1-M\alpha \gamma {t}_{f}\right)}^{k}} $ is a power series tending to zero and $ \mathit{exp}\left(\frac{M\alpha \gamma {t}_{f}}{1-M\alpha \gamma {t}_{f}}\right) $ is a constant. Then:
| $ \underset{k\to \infty }{lim}‖{x}^{(k+j)}\left(t\right)-{x}^{\left(k\right)}\left(t\right)‖ = 0 $ | (30) |
That is to say, for any number j, the sequence $ \left\{{x}^{\left(k\right)}\right(t\left)\right\} $ is a Cauchy sequence, which is the only solution uniformly convergent to system (8). The proof is complete.
Theorem 2 Assuming that the solution sequence of the constructed two-point boundary value problem is $ \left\{{x}^{\left(k\right)}\right(t\left)\right\} $ and the control sequence is $ \left\{{u}^{\left(k\right)}\right(t\left)\right\} $, they converge uniformly to the optimal state trajectory $ {x}^{*}\left(t\right) $ and the Optimal control theory $ {u}^{*}\left(t\right) $ of the system (8) with respect to the quadratic performance index, respectively.
Prove: According to lemma 1, the sequence $ \left\{{x}^{\left(k\right)}\right(t\left)\right\} $ is uniformly convergent. When $ k\to \infty $, the sequence $ \left\{{x}^{\left(k\right)}\right(t\left)\right\} $ converges uniformly to the optimal trajectory $ {x}^{*}\left(t\right) $ of the system.
It can be seen from the Eqs (8) and (9) that $ \left\{{u}^{\left(k\right)}\right(t\left)\right\} $ is only related to $ \left\{{x}^{\left(k\right)}\right(t\left)\right\} $ and $ Q $. Obviously, $ Q $ is a semi-positive constant matrix, so $ \left\{{u}^{\left(k\right)}\right(t\left)\right\} $ is uniformly convergent. When $ k\to \infty $, $ \left\{{u}^{\left(k\right)}\right(t\left)\right\} $ converges uniformly to the Optimal control theory $ {u}^{*}\left(t\right) $ of the system for the quadratic performance index. The proof is complete.
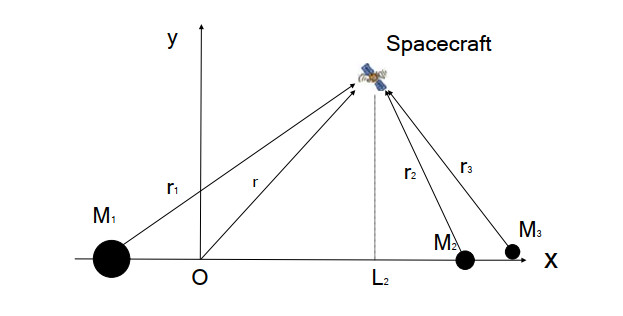
Assume that In the convergent coordinate system, the coordinate origins O are located at the centroid of $ {M}_{1} $, $ {M}_{2} $ and $ {M}_{3} $. Their masses are $ {m}_{1} $, $ {m}_{2} $ and $ {m}_{3} $. The coordinate system schematic diagram of the three-body problem is shown in Figure 1.
According to the dynamic equation of the circular restricted three-body problem in reference 1, it is obtained that:
| $ \left\{\begin{array}{c}\ddot{x}-2\dot{y} = \frac{\partial \varOmega }{\partial x}\\ \ddot{y}-2\dot{x} = \frac{\partial \varOmega }{\partial y}\\ \ddot{z} = \frac{\partial \varOmega }{\partial z}\end{array}\right. $ | (31) |
Let $ \mu = \frac{{m}_{2}+{m}_{3}}{{m}_{1}+{m}_{2}+{m}_{3}} $, $ {\mu }_{0} = \frac{{m}_{3}}{{m}_{1}+{m}_{2}+{m}_{3}} $, $ k = \frac{d}{R} $, where d is the average distance between the earth and the moon, and R is the average distance between the sun and the earth. Then:
| $ \varOmega = {\varOmega }_{1}+{\varOmega }_{2} \\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em} = \left[\frac{1}{2}({x}^{2}+{y}^{2})+\frac{1-\mu }{{r}_{1}}+\frac{\mu }{{r}_{2}}+\frac{1}{2}\mu (1-\mu )\right]+\frac{{\mu }_{0}}{{r}_{3}}-\frac{{\mu }_{0}}{{r}_{2}} $ | (32) |
Where: $ {\varOmega }_{1 } $ is the classical restricted trisomy problem and $ {\varOmega }_{2} $ is the lunar perturbation force.
| $ \left\{\begin{array}{c}{r}_{1}^{2} = (x-\mu {)}^{2}+{y}^{2}+{z}^{2}\\ {r}_{2}^{2} = (x-\mu +1{)}^{2}+{y}^{2}+{z}^{2}\\ {r}_{3}^{2} = (x-\mu -k\mathit{cos}{n}_{1}t{)}^{2}+(y-k\mathit{sin}{n}_{1}t{)}^{2}+{z}^{2}\end{array}\right. $ | (33) |
Where: $ {n}_{1} $ is the average angular velocity of the moon relative to the earth. From Eq (31), it is known that the conditions for the existence of equilibrium solutions are as follows:
| $ \frac{\partial {\varOmega }_{1}}{\partial x} = \frac{\partial {\varOmega }_{1}}{\partial y} = \frac{\partial {\varOmega }_{1}}{\partial z} = 0 $ | (34) |
Five libration points can be solved from Eq (3), of which $ {L}_{4} $ and $ {L}_{5} $ are stable points and $ {L}_{1} $, $ {L}_{2} $ and $ {L}_{3} $ are collinear libration points, which belong to unstable points. This paper chooses the libration point $ {L}_{2} $ of the solar-terrestrial system as the research object.
Assuming the control variable of the main spacecraft is $ {u}^{A} = {\left[\begin{array}{ccc}{u}_{x}^{A}& {u}_{y}^{A}& {u}_{z}^{A}\end{array}\right]}^{T} $, the state vector of the master spacecraft is defined as:
| $\begin{gathered} {X^A} = {\left[ {\begin{array}{*{20}{c}} {{x^A}}&{{{\dot x}^A}}&{{y^A}}&{{{\dot y}^A}}&{{z^A}}&{{{\dot z}^A}} \end{array}} \right]^T} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\left[ {\begin{array}{*{20}{c}} {x_1^A}&{x_2^A}&{x_3^A}&{x_4^A}&{x_5^A}&{x_6^A} \end{array}} \right]^T} \\ \end{gathered} $ | (35) |
Then, the equation of state of the system is:
| $ \left\{\begin{array}{c}{\dot{x}}_{1}^{A} = {x}_{2}^{A}\\ {\dot{x}}_{2}^{A} = 2{x}_{4}^{A}+{x}_{1}^{A}-\frac{({x}_{1}^{A}+\mu )(1-\mu )}{({r}_{1}^{A}{)}^{3}}-\frac{(\mu -{\mu }_{0})[{x}_{1}^{A}-(1-\mu \left)\right]}{({r}_{2}^{A}{)}^{3}}-\frac{{\mu }_{0}({x}_{1}^{A}-\mu -k\mathit{cos}{n}_{1}t)}{({r}_{3}^{A}{)}^{3}}+{u}_{x}^{A}\\ {\dot{x}}_{3}^{A} = {x}_{4}^{A}\\ {\dot{x}}_{4}^{A} = -2{x}_{2}^{A}+{x}_{3}^{A}-\frac{(1-\mu ){x}_{3}^{A}}{({r}_{1}^{A}{)}^{3}}-\frac{(\mu -{\mu }_{0}){x}_{3}^{A}}{({r}_{2}^{A}{)}^{3}}-\frac{{\mu }_{0}({x}_{3}^{A}-k\mathit{sin}{n}_{1}t)}{({r}_{3}^{A}{)}^{3}}+{u}_{y}^{A}\\ {\dot{x}}_{5}^{A} = {x}_{6}^{A}\\ {\dot{x}}_{6}^{A} = \frac{(1-\mu ){x}_{5}^{A}}{({r}_{1}^{A}{)}^{3}}-\frac{(\mu -{\mu }_{0}){x}_{5}^{A}}{({r}_{2}^{A}{)}^{3}}-\frac{{\mu }_{0}{x}_{5}^{A}}{({r}_{3}^{A}{)}^{3}}+{u}_{z}^{A}\end{array}\right. $ | (36) |
Similarly, the equation of state of the slave spacecraft system is as follows:
| $ \left\{\begin{array}{c}{\dot{x}}_{1}^{B} = {x}_{2}^{B}\\ {\dot{x}}_{2}^{B} = 2{x}_{4}^{B}+{x}_{1}^{B}-\frac{({x}_{1}^{B}+\mu )(1-\mu )}{({r}_{1}^{B}{)}^{3}}-\frac{(\mu -{\mu }_{0})[{x}_{1}^{B}-(1-\mu \left)\right]}{({r}_{2}^{B}{)}^{3}}-\frac{{\mu }_{0}({x}_{1}^{B}-\mu -k\mathit{cos}{n}_{1}t)}{({r}_{3}^{B}{)}^{3}}+{u}_{x}^{B}\\ {\dot{x}}_{3}^{B} = {x}_{4}^{B}\\ {\dot{x}}_{4}^{B} = -2{x}_{2}^{B}+{x}_{3}^{B}-\frac{(1-\mu ){x}_{3}^{B}}{({r}_{1}^{B}{)}^{3}}-\frac{(\mu -{\mu }_{0}){x}_{3}^{B}}{({r}_{2}^{B}{)}^{3}}-\frac{{\mu }_{0}({x}_{3}^{B}-k\mathit{sin}{n}_{1}t)}{({r}_{3}^{B}{)}^{3}}+{u}_{y}^{B}\\ {\dot{x}}_{5}^{B} = {x}_{6}^{B}\\ {\dot{x}}_{6}^{B} = \frac{(1-\mu ){x}_{5}^{B}}{({r}_{1}^{B}{)}^{3}}-\frac{(\mu -{\mu }_{0}){x}_{5}^{B}}{({r}_{2}^{B}{)}^{3}}-\frac{{\mu }_{0}{x}_{5}^{B}}{({r}_{3}^{B}{)}^{3}}+{u}_{z}^{B}\end{array}\right. $ | (37) |
The relative motion diagram of spacecraft in the libration point orbit is shown in Figure 2. The relative motion equation of the spacecraft can be obtained by subtracting equation (36) from Eq (37) as follows:
| $ \ddot{r} = {\ddot{r}}^{B}-{\ddot{r}}^{A} $ | (38) |
| $ \left\{\begin{array}{c}{\dot{x}}_{1} = {x}_{2}\\ \begin{array}{c}{\dot{x}}_{2} = 2{x}_{4}+{x}_{1}+(1-\mu )\left[\frac{{x}_{1}^{A}+\mu }{({r}_{1}^{A}{)}^{3}}-\frac{({x}_{1}^{A}+{x}_{1})+\mu }{{‖{r}_{1}^{A}+\rho ‖}^{3}}\right]+(\mu -{\mu }_{0})\left[\frac{{x}_{1}^{A}-(1-\mu )}{({r}_{2}^{A}{)}^{3}}-\frac{({x}_{1}^{A}+{x}_{1})-(1-\mu )}{{‖{r}_{2}^{A}+\rho ‖}^{3}}\right]\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}+{\mu }_{0}\left[\frac{{x}_{1}^{A}-\mu -k\mathit{cos}{n}_{1}t}{({r}_{3}^{A}{)}^{3}}-\frac{({x}_{1}^{A}+{x}_{1})-\mu -k\mathit{cos}{n}_{1}t}{{‖{r}_{3}^{A}+\rho ‖}^{3}}\right]+{u}_{x}\end{array}\\ {\dot{x}}_{3} = {x}_{4}\\ \begin{array}{c}{\dot{x}}_{4} = -2{x}_{2}+{x}_{3}+(1-\mu )\left[\frac{{x}_{3}^{A}}{({r}_{1}^{A}{)}^{3}}-\frac{{x}_{3}^{A}+{x}_{3}}{{‖{r}_{1}^{A}+\rho ‖}^{3}}\right]+(\mu -{\mu }_{0})\left[\frac{{x}_{3}^{A}}{({r}_{2}^{A}{)}^{3}}-\frac{{x}_{3}^{A}+{x}_{3}}{{‖{r}_{2}^{A}+\rho ‖}^{3}}\right]\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}+{\mu }_{0}\left[\frac{{x}_{3}^{A}-k\mathit{sin}{n}_{1}t}{({r}_{3}^{A}{)}^{3}}-\frac{({x}_{3}^{A}+{x}_{3})-k\mathit{sin}{n}_{1}t}{{‖{r}_{3}^{A}+\rho ‖}^{3}}\right]+{u}_{y}\end{array}\\ {\dot{x}}_{5} = {x}_{6}\\ {\dot{x}}_{6} = (1-\mu )\left[\frac{{x}_{5}^{A}}{({r}_{1}^{A}{)}^{3}}-\frac{{x}_{5}^{A}+{x}_{5}}{{‖{r}_{1}^{A}+\rho ‖}^{3}}\right]+(\mu -{\mu }_{0})\left[\frac{{x}_{5}^{A}}{({r}_{2}^{A}{)}^{3}}-\frac{{x}_{5}^{A}+{x}_{5}}{{‖{r}_{2}^{A}+\rho ‖}^{3}}\right]+{\mu }_{0}\left[\frac{{x}_{5}^{A}}{({r}_{3}^{A}{)}^{3}}-\frac{{x}_{5}^{A}+{x}_{5}}{{‖{r}_{3}^{A}+\rho ‖}^{3}}\right]+{u}_{z}\end{array}\right. $ | (39) |
Where: $ {u}_{x} = {u}_{x}^{B}-{u}_{x}^{A} $, $ {u}_{y} = {u}_{y}^{B}-{u}_{y}^{A} $, $ {u}_{z} = {u}_{z}^{B}-{u}_{z}^{A} $, $ {x}_{i} = {x}_{i}^{B}-{x}_{i}^{A}(i = \mathrm{1, 2}, \cdots, 6) $.
The above relative motion equation is written in a general form:
The master spacecraft:
| $ {\dot{x}}^{A} = {f}^{A}\left({x}^{A}\right)+{u}^{A} $ | (40) |
The slave spacecraft:
| $ {\dot{x}}^{B} = {f}^{B}({x}^{A}, x)+{u}^{B} $ | (41) |
The Optimal control method can be used to design the controller of the master spacecraft separately. The improved successive approximation method is used to design the controller of the slave spacecraft. In order to use the improved successive approximation method, condition $ f\left(0\right) = 0 $ needs to be satisfied. But the following terms in equation of motion (33) will deviate.
| $ (1-\mu )\left[\frac{{x}_{1}^{A}+\mu }{({r}_{1}^{A}{)}^{3}}-\frac{({x}_{1}^{A}+{x}_{1})+\mu }{{‖{r}_{1}^{A}+\rho ‖}^{3}}\right]\\ +(\mu -{\mu }_{0})\left[\frac{{x}_{1}^{A}-(1-\mu )}{({r}_{2}^{A}{)}^{3}}-\frac{({x}_{1}^{A}+{x}_{1})-(1-\mu )}{{‖{r}_{2}^{A}+\rho ‖}^{3}}\right]\\ +{\mu }_{0}\left[\frac{{x}_{1}^{A}-\mu -k\mathit{cos}{n}_{1}t}{({r}_{3}^{A}{)}^{3}}-\frac{({x}_{1}^{A}+{x}_{1})-\mu -k\mathit{cos}{n}_{1}t}{{‖{r}_{3}^{A}+\rho ‖}^{3}}\right] $ |
As well as the following two terms in the above formula, the Eq (33) is deviated and the system state cannot be zero. For this reason, these effects need to be eliminated.
| $ (1-\mu )\left[\frac{{x}_{3}^{A}}{({r}_{1}^{A}{)}^{3}}-\frac{{x}_{3}^{A}+{x}_{3}}{{‖{r}_{1}^{A}+\rho ‖}^{3}}\right]+(\mu -{\mu }_{0})\left[\frac{{x}_{3}^{A}}{({r}_{2}^{A}{)}^{3}}-\frac{{x}_{3}^{A}+{x}_{3}}{{‖{r}_{2}^{A}+\rho ‖}^{3}}\right]\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}+{\mu }_{0}\left[\frac{{x}_{3}^{A}-k\mathit{sin}{n}_{1}t}{({r}_{3}^{A}{)}^{3}}-\frac{({x}_{3}^{A}+{x}_{3})-k\mathit{sin}{n}_{1}t}{{‖{r}_{3}^{A}+\rho ‖}^{3}}\right] $ |
And,
| $ (1-\mu )\left[\frac{{x}_{5}^{A}}{({r}_{1}^{A}{)}^{3}}-\frac{{x}_{5}^{A}+{x}_{5}}{{‖{r}_{1}^{A}+\rho ‖}^{3}}\right]+(\mu -{\mu }_{0})\left[\frac{{x}_{5}^{A}}{({r}_{2}^{A}{)}^{3}}-\frac{{x}_{5}^{A}+{x}_{5}}{{‖{r}_{2}^{A}+\rho ‖}^{3}}\right]\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\\ +{\mu }_{0}\left[\frac{{x}_{5}^{A}}{({r}_{3}^{A}{)}^{3}}-\frac{{x}_{5}^{A}+{x}_{5}}{{‖{r}_{3}^{A}+\rho ‖}^{3}}\right] $ |
In this paper, $ {\dot{s}}_{1} = -{\lambda }_{1}{s}_{1} $ and $ {\dot{s}}_{2} = -{\lambda }_{2}{s}_{2} $ are used to eliminate the influence of deviation term. The following equations can be obtained from the equation of relative motion (33):
$ A = \left[\begin{array}{cccccccc}0& 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 2& 0& 0& {a}_{27}& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& -2& 1& 0& 0& 0& 0& {a}_{48}\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& {a}_{65}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& {\lambda }_{1}& 0\\ 0& 0& 0& 0& 0& 0& 0& {\lambda }_{2}\end{array}\right] $, $ B = \left[\begin{array}{ccc}0& 0& 0\\ 1& 0& 0\\ 0& 0& 0\\ 0& 1& 0\\ 0& 0& 0\\ 0& 0& 1\\ 0& 0& 0\\ 0& 0& 0\end{array}\right] $,
$ f\left(x\right) = \left[\begin{array}{c}0\\ {b}_{27}\\ 0\\ {b}_{48}\\ 0\\ {b}_{65}\end{array}\right] $, $ G\left(x\right) = \left[\begin{array}{c}\mathrm{0, 0}, \mathrm{0, 0}, \mathrm{0, 0}\\ {b}_{27}/{x}_{1}, \mathrm{0, 0}, \mathrm{0, 0}, 0\\ \mathrm{0, 0}, \mathrm{0, 0}, \mathrm{0, 0}\\ \mathrm{0, 0}, {b}_{48}/{x}_{3}, \mathrm{0, 0}, 0\\ \mathrm{0, 0}, \mathrm{0, 0}, \mathrm{0, 0}\\ \mathrm{0, 0}, \mathrm{0, 0}, {b}_{65}/{x}_{5}, 0\end{array}\right] $.
Where:
| $ {a}_{27} = (1-\mu )\left[\frac{{x}_{1}^{A}+\mu }{({r}_{1}^{A}{)}^{3}{s}_{1}}-\frac{{x}_{1}^{A}+\mu }{{‖{r}_{1}^{A}+\rho ‖}^{3}{s}_{1}}\right]+(\mu -{\mu }_{0})\left[\frac{{x}_{1}^{A}-(1-\mu )}{({r}_{2}^{A}{)}^{3}{s}_{1}}-\frac{{x}_{1}^{A}-(1-\mu )}{{‖{r}_{2}^{A}+\rho ‖}^{3}{s}_{1}}\right]+{\mu }_{0}\left[\frac{{x}_{1}^{A}-\mu -k\mathit{cos}{n}_{1}t}{({r}_{3}^{A}{)}^{3}{s}_{1}}-\frac{{x}_{1}^{A}-\mu -k\mathit{cos}{n}_{1}t}{{‖{r}_{3}^{A}+\rho ‖}^{3}{s}_{1}}\right] $ |
| $ {b}_{27} = -(1-\mu )\frac{{x}_{1}}{{‖{r}_{1}^{A}+\rho ‖}^{3}{s}_{1}}-(\mu -{\mu }_{0})\frac{{x}_{1}}{{‖{r}_{2}^{A}+\rho ‖}^{3}{s}_{1}}-{\mu }_{0}\frac{{x}_{1}}{{‖{r}_{3}^{A}+\rho ‖}^{3}{s}_{1}} $ |
| $ {a}_{48} = (1-\mu )\left[\frac{{x}_{3}^{A}}{({r}_{1}^{A}{)}^{3}{s}_{2}}-\frac{{x}_{3}^{A}}{{‖{r}_{1}^{A}+\rho ‖}^{3}{s}_{2}}\right]+(\mu -{\mu }_{0})\left[\frac{{x}_{3}^{A}}{({r}_{2}^{A}{)}^{3}{s}_{2}}-\frac{{x}_{3}^{A}}{{‖{r}_{2}^{A}+\rho ‖}^{3}{s}_{2}}\right] $ |
| $ +{\mu }_{0}\left[\frac{{x}_{3}^{A}-k\mathit{sin}{n}_{1}t}{({r}_{3}^{A}{)}^{3}{s}_{2}}-\frac{{x}_{3}^{A}-k\mathit{sin}{n}_{1}t}{{‖{r}_{3}^{A}+\rho ‖}^{3}{s}_{2}}\right] $ |
| $ {b}_{48} = -(1-\mu )\frac{{x}_{3}}{{‖{r}_{1}^{A}+\rho ‖}^{3}{s}_{2}}-(\mu -{\mu }_{0})\frac{{x}_{3}}{{‖{r}_{2}^{A}+\rho ‖}^{3}{s}_{2}}-{\mu }_{0}\frac{{x}_{3}}{{‖{r}_{3}^{A}+\rho ‖}^{3}{s}_{2}} $ |
| $ {a}_{65} = (1-\mu )\left[\frac{{x}_{5}^{A}}{({r}_{1}^{A}{)}^{3}}-\frac{{x}_{5}^{A}}{{‖{r}_{1}^{A}+\rho ‖}^{3}}\right]+(\mu -{\mu }_{0})\left[\frac{{x}_{5}^{A}}{({r}_{2}^{A}{)}^{3}}-\frac{{x}_{5}^{A}}{{‖{r}_{2}^{A}+\rho ‖}^{3}}\right] $ |
| $ +{\mu }_{0}\left[\frac{{x}_{5}^{A}}{({r}_{3}^{A}{)}^{3}}-\frac{{x}_{5}^{A}}{{‖{r}_{3}^{A}+\rho ‖}^{3}}\right] $ |
| $ {b}_{65} = -(1-\mu )\frac{{x}_{5}}{{‖{r}_{1}^{A}+\rho ‖}^{3}}-(\mu -{\mu }_{0})\frac{{x}_{5}}{{‖{r}_{2}^{A}+\rho ‖}^{3}}-{\mu }_{0}\frac{{x}_{5}}{{‖{r}_{3}^{A}+\rho ‖}^{3}} $ |
The quadratic performance index function is selected as follows:
| $ J = \frac{1}{2}{\int }_{0}^{\infty }\left[{x}^{T}\right(t\left)Qx\right(t)+{u}^{T}(t\left)Ru\right(t\left)\right]dt $ | (42) |
Set the control precision to: $ \varepsilon = 0.01 $.
In the numerical example, the master spacecraft in halo orbit of L2 point of solar-earth system is adopted. Halo orbit is a kind of special orbit, which can maintain spacecraft in space without consuming too much fuel. It is an approximate circular orbit formed on the equilibrium point (translation point) when multiple gravitational sources act on spacecraft. The first application of halo orbit was the international comet probe launched in 1978. It marched to L1 point of solar-earth system and stayed there for several years. Because of its particularity, it is usually used as an important observation point in space missions. The specific values are as follows:
$ {x}_{0} = 87028.508409273 $ km, $ {y}_{0} = -24739.51269980 $ km, $ {z}_{0} = -229952.974656271 $ km, $ {\dot{x}}_{0} = -8.985877859 $ m/s, $ {\dot{y}}_{0} = -121.605674977 $ m/s, $ {\dot{z}}_{0} = 9.457953755 $ m/s.
According to the calculation method of the improved successive approximation method, the calculation is carried out according to algorithm 1. After seven iterations, their performance index $ {J}^{\left(k\right)} $ and its convergence index $ {J}_{e}^{\left(k\right)} $ are calculated. The calculation results are shown in Table 1.
| Number of iterations: k | performance index: $ {J}^{\left(k\right)} $ | $ \frac{{J}^{\left(k\right)}-{J}^{(k-1)}}{{J}^{\left(k\right)}} $ |
| 1 | 7.3320 | |
| 2 | 6.1780 | -0.2385 |
| 3 | 4.9883 | -0.0625 |
| 4 | 4.6949 | -0.0050 |
| 5 | 4.6715 | -0.0015 |
| 6 | 4.6645 | -0.0003 |
| 7 | 4.6632 | 0.0000 |
It can be seen from Table 1 that performance indicators $ {J}^{\left(k\right)} $ and $ {J}_{e}^{\left(k\right)} $ are convergent, which indicates that performance index $ J $ is uniformly convergent. The tracking error e(t) of the system tends to zero in the optimal way. As for the selection of parameter K, when the performance index $ {J}^{\left(k\right)} $ is basically unchanged, that is, when the difference between the performance index $ {J}^{\left(k\right)} $ of this iteration and the performance index $ {J}^{(k-1)} $ of the previous iteration is close to zero, the value of K is the last iteration.
The relative initial conditions for formation are:
| $ {\left[\begin{array}{cccccc}x\left(0\right)& \dot{x}\left(0\right)& y\left(0\right)& \dot{y}\left(0\right)& z\left(0\right)& \dot{z}\left(0\right)\end{array}\right]}^{T} = {\left[\begin{array}{cccccc}5& 0& 5& 0& 5& 0\end{array}\right]}^{T} $ |
Figure 3 shows the tracking error $ {e}_{x} $, $ {e}_{y} $, $ {e}_{z} $. Where: $ ({e}_{x}, {e}_{y}, {e}_{z}) = ({x}_{r}-x, {y}_{r}-y, {z}_{r}-z) $, and $ {e}_{r} = \sqrt{{e}_{x}^{2}+{e}_{y}^{2}+{e}_{z}^{2}} $. In order to clearly represent the instantaneous response of the error, Figure 4 provides the error history of the first day. The error dropped quickly to near zero in one day. As can be seen from Figure 4, the error after two days fluctuated within a range of 10mm. Figures 5 and 6 show the control history of formation flight. As can be seen from Figure 5, the control force drops rapidly from 4 $ N $ to near zero. From Figure 6, it can be seen that the average control force to keep formation flying is about 250 $ \mu N $.
In this paper, a non-linear dynamic model of formation flying is established by derivation. After proving the convergence of the improved successive approximation, a formation flight controller is designed. According to the improved successive approximation algorithm, the performance index function is iterated for seven times, and good convergence is obtained. Finally, the error and control simulations of the formation flying of the spacecraft with the libration points of the solar-earth system are carried out for two days. The simulation results show that the error decreases to near zero in one day and fluctuates in the range of 10 mm after two days. The control power on the first day dropped quickly from 4 $ N $ to near zero, and the average control force after two days was about 250 $ \mu N $. The results show that the method has the advantages of high control accuracy and short control time in formation keeping control of solar-earth libration points. The disadvantage is that the calculation is complicated. But, with the development of computer technology, it will have a certain practical value in the future research of team maintenance control.
Recently, convex optimization method is becoming more and more popular [12]. Convex optimization method is mostly used in artificial intelligence technology. Recently, the author also tries to use convex optimization method to study formation flight keeping control. In order to achieve better control results. Of course, the control effect of the improved successive approximation method is the highest in terms of accuracy. However, the convex optimization method can greatly reduce the amount of computation and obtain better computational efficiency. The research of convex optimization in formation flight control technology will not be described here, but will be described in another paper of the author.
The authors acknowledge the National Natural Science Foundation of China (Grant: 61174202), the National Natural Science Foundation of China (Grant: 61502391), the 13th Five-Year Plan of Shaanxi Province in 2020 (Gant: GH20Y649), School level scientific research pro-jects(Gant:33/115040393, Gant:33/115040441).
The authors declare that they have no competing interests.
| [1] |
S. Carletta, M. Pontani, P. Teofilatto, Dynamics of three-dimensional capture or-bits from libration region analysis, Acta Astronaut., 165 (2019), 331-343. doi: 10.1016/j.actaastro.2019.09.019

|
| [2] |
G. Pinzari, Perihelion Librations in the Secular Three-Body Problem, J. Nonlinear Sci., 30 (2020), 1771-1808. doi: 10.1007/s00332-020-09624-x

|
| [3] |
S. Wu, Design of interactive digital media course teaching information query system, Inf. Syst. e-Business Manage., 18 (2020), 793-807. doi: 10.1007/s10257-018-00397-1

|
| [4] |
J. Duan, Z. Wang, Orbit determination of CE-4's relay satellite in Earth-Moon L2 libration point orbit, Adv. Space Res., 64 (2019), 2345-2355. doi: 10.1016/j.asr.2019.08.012

|
| [5] | N. Hong, C. T. del Busto, Collaboration, Scaffolding and Successive Approximations: A Developmental Science Approach to Training in Clinical Psychology, Train. Educ. Prof. Psychol., 14 (2020), 228-234. |
| [6] | H. Peng, J. Zhao, Z. Wu, W. Zhong, Optimal periodic controller for formation flying on libration point orbits, Acta Astronaut., 69 (2020), 537-550. |
| [7] |
H. Peng, X. Jiang, B. Chen, Optimal nonlinear feedback control of spacecraft ren-dezvous with finite low thrust between libration orbits, Nonlinear Dyn., 76 (2014), 1611-1632. doi: 10.1007/s11071-013-1233-9

|
| [8] | Y. Jiang, Equilibrium points and orbits around asteroid with the full gravitational potential caused by the 3D irregular shape. Astrodynamics, 14 (2018), 361-373. |
| [9] |
H. Peng, X. Jiang, Nonlinear Receding Horizon Guidance for Spacecraft Formation Re-configuration on Libration Point Orbits using a Symplectic Numerical Method, ISA Trans., 60 (2016), 38-52. doi: 10.1016/j.isatra.2015.10.015

|
| [10] |
R. Chai, A. Tsourdos, A. Savvaris, S. Chai, Y. Xia, C. P. Chen, Six-DOF Spacecraft Optimal Trajectory Planning and Real-Time Attitude Control: A Deep Neural Network-Based Approach, IEEE Trans. Neural Networks Learn. Syst., 31 (2020), 5005-5013. doi: 10.1109/TNNLS.2019.2955400

|
| [11] |
R. Chai, A. Tsourdos, A. Savvaris, S. Chai, Y. Xia, Trajectory planning for hyper-sonic reentry vehicle satisfying deterministic and probabilistic constraints, Acta Astronaut., 177 (2020), 30-38. doi: 10.1016/j.actaastro.2020.06.051

|
| [12] |
W. Zhao, T. Shi, L. Wang, Fault Diagnosis and Prognosis of Bearing Based on Hidden Markov Model with Multi-Features, Appl. Math. Nonlinear Sci., 5 (2020), 71-84. doi: 10.2478/amns.2020.1.00008

|
| [13] |
K. Zhang, Z. He, M. Lv, Study on maintaining formations during satellite formation flying based on SDRE and LQR, Open Phys., 15 (2017), 394-399. doi: 10.1515/phys-2017-0043

|
| [14] |
Y. Zhao, Analysis of Trade Effect in Post-Tpp Era: Based on Gravity Model and Gtap Model, Appl. Math. Nonlinear Sci., 5 (2020), 61-70. doi: 10.2478/amns.2020.1.00007

|
| [15] |
L. Li, Y. Wang, X. Li, Tourists Forecast Lanzhou Based on the Baolan High-Speed Railway by the Arima Model, Appl. Math. Nonlinear Sci., 5 (2020), 55-60. doi: 10.2478/amns.2020.1.00006

|
| [16] |
T. Li, W. Yang, Solution to Chance Constrained Programming Problem in Swap Trailer Transport Organisation based on Improved Simulated Annealing Algorithm, Appl. Math. Nonlinear Sci., 5 (2020), 47-54. doi: 10.2478/amns.2020.1.00005

|
| [17] | Y. Wang, G. Zhang, Z. Shi, Finite-time active disturbance rejection control for marine diesel engine, Appl. Math. Nonlinear Sci., 5 (2020), 35-46. |
| [18] | P. Zhou, Q. Fan, J. Zhu, Empirical Analysis on Environmental Regulation Performance Measurement in Manufacturing Industry: A Case Study of Chongqing, China, Appl. Math. Nonlinear Sci., 5 (2020), 25-34. |
| [19] |
R. A. de Assis, R. Pazim, M. C. Malavazi, A Mathematical Model to describe the herd behaviour considering group defense, Appl. Math. Nonlinear Sci., 5 (2020), 11-24. doi: 10.2478/amns.2020.1.00002

|
| [20] | T. Xie, R. Liu, Z. Wei, Improvement of the Fast Clustering Algorithm Improved by K-Means in the Big Data, Appl. Math. Nonlinear Sci., 5 (2020), 1-10. |
| [21] | B. Shanmukha, V. Venkatesha, Some Results on Generalized Sasakian Space Forms, Appl. Math. Nonlinear Sci., 5 (2020), 85-92. |
| [22] |
M. El-Borhamy, N. Mosalam, On the existence of periodic solution and the transition to chaos of Rayleigh-Duffing equation with application of gyro dynamic, Appl. Math. Nonlinear Sci., 5 (2020), 93-108. doi: 10.2478/amns.2020.1.00010

|
| [23] | H. Günerhan, E. Çelik, Analytical and approximate solutions of Fractional Partial Dif-ferential-Algebraic Equations, Appl. Math. Nonlinear Sci., 5 (2020), 109-120. |
| [24] | T. Li, L. Qiao, Y. Ding, Factors Influencing the Cooperative Relationship between Enterprises in the Supply Chain of China's Marine Engineering Equipment Manufacturing Industry-An study based on GRNN-DEMATEL method, Appl. Math. Nonlinear Sci., 5 (2020), 121-138. |
| 1. | Sai Zhang, Li Tang, Yan-Jun Liu, Formation deployment control of multi-agent systems modeled with PDE, 2022, 19, 1551-0018, 13541, 10.3934/mbe.2022632 | |
| 2. | Xingji He, Ming Xu, Xiucong Sun, Na Peng, Liang Wang, Lei Liu, Naturally bounded relative motion for formation flying near triangular libration points, 2023, 02731177, 10.1016/j.asr.2023.02.013 |
| Number of iterations: k | performance index: $ {J}^{\left(k\right)} $ | $ \frac{{J}^{\left(k\right)}-{J}^{(k-1)}}{{J}^{\left(k\right)}} $ |
| 1 | 7.3320 | |
| 2 | 6.1780 | -0.2385 |
| 3 | 4.9883 | -0.0625 |
| 4 | 4.6949 | -0.0050 |
| 5 | 4.6715 | -0.0015 |
| 6 | 4.6645 | -0.0003 |
| 7 | 4.6632 | 0.0000 |