Citation: D. Clayton John. Phase Field Theory and Analysis of Pressure-Shear Induced Amorphization and Failure in Boron Carbide Ceramic[J]. AIMS Materials Science, 2014, 1(3): 143-158. doi: 10.3934/matersci.2014.3.143
| [1] | Nuriya М. Mukhamedova, Mazhyn K. Skakov, Wojciech Wieleba . Determination of phase composition and mechanical properties of surface of the material obtained on the basis of silicon and carbon by spark-plasma sintering method. AIMS Materials Science, 2019, 6(1): 1-9. doi: 10.3934/matersci.2019.1.1 |
| [2] | Alexander Umantsev . Continuum theory of amorphous nanophases. AIMS Materials Science, 2016, 3(1): 22-34. doi: 10.3934/matersci.2016.1.22 |
| [3] | Mohamed Lokman Jalaluddin, Umar Al-Amani Azlan, Mohd Warikh Abd Rashid, Norfauzi Tamin . Effect of sintering temperatures on the physical, structural properties and microstructure of mullite-based ceramics. AIMS Materials Science, 2024, 11(2): 243-255. doi: 10.3934/matersci.2024014 |
| [4] | Tomas Melus, Roman Kolenak, Jaromir Drapala, Mikulas Sloboda, Peter Gogola, Matej Pasak . Research of joining the SiC and Cu combination by use of SnTi solder filled with SiC nanoparticles and with active ultrasound assistance. AIMS Materials Science, 2024, 11(5): 1013-1034. doi: 10.3934/matersci.2024048 |
| [5] | Hanh C. Nguyen, Shigeru Nagasawa, Kensei Kaneko . Strength estimation of silicon nitride ceramics using a round-notched specimen subjected to shearing-tool indentation. AIMS Materials Science, 2020, 7(5): 518-533. doi: 10.3934/matersci.2020.5.518 |
| [6] | Valeriy Ishchuk, Danil Kuzenko, Vladimir Sobolev . Piezoelectric and functional properties of materials with coexisting ferroelectric and antiferroelectric phases. AIMS Materials Science, 2018, 5(4): 711-741. doi: 10.3934/matersci.2018.4.711 |
| [7] | Mohamed Lokman Jalaluddin, Umar Al-Amani Azlan, Mohd Warikh Abd Rashid . A preliminary study of porous ceramics with carbon black contents. AIMS Materials Science, 2023, 10(5): 741-754. doi: 10.3934/matersci.2023041 |
| [8] | Frank Tietz . Phase relations of NASICON materials and compilation of the quaternary phase diagram Na2O-P2O5-SiO2-ZrO2. AIMS Materials Science, 2017, 4(6): 1305-1318. doi: 10.3934/matersci.2017.6.1305 |
| [9] | Aleksander Panichkin, Alma Uskenbayeva, Aidar Kenzhegulov, Axaule Mamaeva, Balzhan Kshibekova, Zhassulan Alibekov . The influence of cooling rate on the structure and properties of castings of hypereutectic high-chromium cast iron when they are modified with B, Bi, Sb, Sn, Ca. AIMS Materials Science, 2024, 11(1): 58-80. doi: 10.3934/matersci.2024003 |
| [10] | Luca Spiridigliozzi, Grazia Accardo, Emilio Audasso, Barbara Bosio, Sung Pil Yoon, Gianfranco Dell’Agli . Synthesis of easily sinterable ceramic electrolytes based on Bi-doped 8YSZ for IT-SOFC applications. AIMS Materials Science, 2019, 6(4): 610-620. doi: 10.3934/matersci.2019.4.610 |
Many crystalline ceramics and minerals undergo structural changes (e.g., phase transformations, twinning, or fracture) when subjected to stresses of high magnitude. One such structural transition is amorphization, i.e., transformation from a crystalline structure to an amorphous/glassy phase lacking long-range order. Under mechanical loading by large compressive and /or shear stress, such amorphization may occur, for example, in quartz (a-SiO2; rhombohedral crystal structure) [1], berlinite (a-AlPO4; rhombohedral structure) [2], some forms of garnet (Y3Al5O12; cubic structure) [3], and boron carbide (nominally B4C, with varying carbon content possible; rhombohedral) [4]. Noteworthy among all of these materials is a loss of static or dynamic shear stiffness with increasing pressure. According to a theoretical criterion attributed first to Born [5] and advanced in subsequent literature [6, 7, 8], attainment of null stiffness in one or more preferred directions, which can be associated with loss of positive-definiteness of a certain tangent elastic stiffness tensor depending on loading protocol, may signal onset of a localized structural transformation such as amorphization.
The present paper focuses on boron carbide, a strong ceramic of high stiffness, high hardness, low mass density, and low ductility. Different structural variants of boron carbide exist, called polytypes. Atomic chains consisting of C-C-C or C-B-C are aligned parallel to the [0001] direction (hexagonal Miller indices) and thread basal layers of icosahedra at the rhombohderal vertices of the unit cell. Polytypes may differ in stoichiometry, ground state energy, elastic stiffness, and amorphization tendency [9, 10, 11]. One model for amorphization based on results of Density Functional Theory (DFT) calculations suggests that structural collapse and localization follow cross-linking of the C-B-C chain with icosahedral atoms [4]; other calculations suggest segregation is most favorable for polytypes with C-C-C chains [9]. More recent DFT calculations [12] demonstrate amorphization in both classes of polytype under uniaxial loading. In physical experiments, amorphization of boron carbide has been observed in Diamond Anvil Cell (DAC) compression-decompression [4], indentation [13], and ballistic impact [14]. Regarding the latter, performance of boron carbide ceramic in protection systems such as armor for vehicles and personnel is thought to be severely impeded by its tendency to localize, with cleavage fracture accompanying or closely following amorphization [14]. In recovered samples, regions of glassy phase are often reported to be in the form of planar b and s of small thickness, on the order of several nanometers, and may be preferentially located parallel to certain crystallographic planes [4, 14].
In order to facilitate design of structures and composite material systems for defense and industrial applications, continuum scale models are needed for predicting localization and failure in boron carbide ceramics. Previous models for the transition from crystalline to glassy phase include one based on adiabatic shear localization [15] and another in which instability is triggered by loss of nonlinear elastic tangent stiffness [16, 17] similar to Born’s criterion. In contrast, the present paper invokes nonlinear continuum phase field theory, in what appears to be the first known application of phase field modeling towards stress-induced amorphization.
In the phase field approach, the thermodynamic state of the material is described, locally and in part, by one or more order parameters. Elastic strain energy density generally depends on order parameter (s) , as does surface energy, the latter reflected by dependence of total energy on spatial gradients of the order parameter (s) . Phase field models have been applied to describe numerous kinds of structural changes in crystalline materials, including dislocation glide [18], twinning [19, 20, 21], and fracture [22, 23, 24, 25]. Advantages of phase field methods over other continuum models for crystal plasticity, twinning, and fracture in metals [26] and ceramics [27, 28, 29] include the following: (i) relatively few material parameters are needed, (ii) evolution laws for inelastic deformation mechanisms follow naturally from energy minimization and need not be prescribed ad hoc, and (iii) an intrinsic length scale is introduced via the surface energy, enabling regularization of localization zones and mesh independent numerical results. Regarding the latter advantage, the need for explicit tracking of sharp interfaces is avoided in numerical schemes, and st and ard finite element discretizations may be used for solution of boundary value problems.
In the present paper, phase field theory is applied towards amorphization in a way similar to prior phase field models for fracture [22, 23, 24, 25], with a single order parameter increasing in value from zero to unity during the transition from crystalline to amorphous phase, and with shear stiffness degrading with increasing order parameter. It is clarified that whereas amorphization can be classified as a true phase transformation, twinning and fracture are not usually categorized as such in a strict sense. Regardless, phase field models tend to treat twinning and fracture analogously to phase changes, wherein evolution of order parameter (s) quantify the transition in state from a perfect parent crystal “phase” to a fully twinned or fully fractured/damaged “phase”. Structural collapse may be accompanied by an inelastic decrease in volume (i.e., increase in mass density) [4], which promotes amorphization with increasing pressure. Thus, under pressure, shear stiffness and strength tend to decrease, in agreement with DFT calculations [10, 11, 12]. In the present paper, a general thermodynamic theory is developed first, accounting for anisotropic elastic strain energy and anisotropic surface energy. Then an idealized nonlinear isotropic theory is developed that facilitates solution of boundary value problems. Specifically, problems involving volumetric compression and simple shear and are studied analytically to demonstrate the predictive ability of the theory. Stability is assessed, extending previous analyses of continuum damage models [30]. Effects of properties particular and peculiar to boron carbide entering the model are explored, providing new insight into the onset of localization and failure. Notation of nonlinear continuum mechanics [31] is used, here primarily in direct form for vectors and tensors which are written in bold font.
Single crystals of boron carbide (B4C) belong to space group R3m, centrosymmetric point group 3m, and Laue group RI, the latter indicative of six independent second-order elastic constants and fourteen independent third-order elastic constants [16, 31]. The theoretical mass density of stoichiometric B4C is 2.52 g×cm-3. Polycrystalline boron carbide has a typical grain size on the order of 10 mm, an elastic modulus on the order of 470 GPa, a hardness on the order of 30 GPa, and a Hugoniot Elastic Limit (HEL, or yield stress under shock compression) on the order of 15-20 GPa [17]. Ductility is low, implying that although full dislocations, partial dislocations, and stacking faults have been observed [32], their low-temperature mobility is inhibited [16]. Twins are thought to arise predominantly during processing [33] rather than to be induced by stress or strain. Primary inelastic deformation mechanisms under impact loading are amorphization and fracture (primarily cleavage fracture on intrinsically weakest planes) , which may occur sequentially or simultaneous ly.
Listed for future reference in Table 1 are physical properties entering the idealized isotropic phase field model of boron carbide to be applied later in analysis of pressure-shear deformation and corresponding instability. Ambient bulk modulus B0 and shear modulus m0 for the fully crystalline phase are obtained, respectively, from a fit of the nonlinear elastic potential function to quantum mechanical equation-of-state data for the polar C-B-C polytype [11] and a Voigt average of the second-order anisotropic constants [29, 31]. Regularization parameter l indicating the width of localized structural transition zones is representative of the thickness of planar glassy phases of boron carbide observed in recovered experimental samples [4, 14]. The surface energy of amorphous zones is computed as the difference between ground state energies (measured per appropriate unit reference volume) of segregated amorphous and crystal phases, multiplied by l, where energy of the polar C-B-C polytype is used for the crystal reference [9]. The ratio of mass density of the crystalline phase to that of the amorphous phase is denoted by X; this value depends on the composition and structure of the glass, here taken as 0.96, corresponding to a 4% volume reduction upon structure collapse commensurate with amorphization [4].
| Property | Description | Value [units] |
| B0 | bulk modulus (crystal) | 248 GPa |
| m0 | shear modulus (crystal) | 197 GPa |
| l | localization width (glass) | 2 nm |
| Γ | surface energy (glass) | 347 mJ×m-2 |
| Ξ | density ratio (crystal/glass) | 0.96 |
General nonlinear, anisotropic, three-dimensional (3D) theory is outlined in §2.2. Model kinematics, energy functions, and governing equations are described in turn.
Let x = x (X, t) denote spatial position at time t of a material particle whose reference position is denoted by X. The deformation gradient is
| \[{\bf{F}} = \nabla {\bf{x}} = \partial x/\partial X\] | (1) |
where Ñ is the material gradient operator. Let xÎ[0,1] denote the scalar order parameter, where
| \[\xi ({\bf{X}},t) \left\{ {\begin{array}{*{20}{c}} {= 0{\rm{ }}}\\ {\in (0,1) }\\ {= 1{\rm{ }}} \end{array}} \right.\begin{array}{*{20}{c}} {\forall {\bf{X}} \in {\rm{crystal phase at time }}t{\rm{ }}}\\ {\forall {\bf{X}} \in {\rm{interface zone at time }}t}\\ {\forall {\bf{X}} \in {\rm{glassy phase at time }}t{\rm{ }}} \end{array}\] | (2) |
The deformation gradient is split multiplicatively into a product of two terms as
| \[{\bf{F}} = {{\bf{F}}^{\rm{E}}}{{\bf{F}}^\xi }\] \[{{\bf{F}}^\xi } ({\bf{X}},t) = {{\bf{F}}^\xi }[\xi ({\bf{X}},t) ]\] | (3) |
where FE is the elastic deformation conjugate to the applied stress and Fx is the inelastic deformation that depends, as indicated, on the local value of the order parameter associated with structural transformation, specifically amorphization. Unlike F, which always obeys compatibility (null curl) conditions Ñ xF = 0, neither FE nor Fx is individually always integrable to a vector field, i.e., these two deformations are generally anholonomic [34]. Note that this theory only accounts explicitly for one type of structural change. Not included in (3) are additional terms needed for representation of effects of other kinds of defects, for example dislocation slip [26, 31], twinning [27], fracture [35], disclination rotation [36], and dilatation associated with stacking faults and dislocation or disclination cores [37, 38] or point defects [39, 40]. The symmetric elastic deformation tensor C and the measure of elastic volume change J are defined as (no “E” superscript)
| \[{\bf{C}} = { ({{\bf{F}}^{\rm{E}}}) ^{\rm{T}}}{{\bf{F}}^{\rm{E}}}\] \[J = \sqrt {\det {\bf{C}}} = \det {{\bf{F}}^{\rm{E}}} = \det F/\det F\] | (4) |
Similar to previous nonlinear phase field theories for twinning [19, 20, 21] and fracture [25], a total energy functional for a body of reference volume V is posited in general form as
| \[\Psi ({\bf{x}},\xi ) = \int_V {[W ({\bf{C}},\xi ) + f (\xi ) + \kappa :\nabla \xi \otimes \nabla \xi ]{\rm{d}}V} \] | (5) |
where W is elastic strain energy density per unit reference volume, f accounts for the difference in ground state energies among crystalline, amorphous, and intermediate phases, and k is a symmetric second-order tensor that accounts for surface energy associated with gradients of the order parameter. For a fully realistic nonlinear anisotropic response, W should reflect the rhombohedral symmetry of the crystalline phase, the importance of higher-order elastic constants [16], and the transition to elastic isotropy upon complete amorphization [17]. In order to restrict amorphous b and s to specific crystallographic planes, the following form of k may be used [25]:
| \[\kappa = {\kappa _0}[1 + \beta (1 - {\bf{m}} \otimes {\bf{m}}) ]\] | (6) |
Here k0 is a scalar and b ³ 0 is a penalty factor that, when greater than zero, increases surface energies on planes not normal to referential unit vector m. If such a representation is insufficient (i.e., if numerous different planes with various surface energies and orientations are prone to localization) , the theory may require extension to distinct order parameters for each plane.
A variational framework is considered henceforth, amenable to solution via energy minimization [19, 20, 21]. Time t becomes a parameter and does not explicitly enter the governing equations, which are now applicable only to quasi-static problems. The following variational principle is set forth:
| \[\delta \Psi = \oint_S {[{\bf{t}} \cdot \delta {\bf{x}} + r\delta \xi ]{\rm{d}}S} \] | (7) |
with t the mechanical traction vector, r a conjugate force to the order parameter, and S the referential surface enclosing V. Application of st and ard mathematical procedures involving integration by parts and the divergence theorem [19, 31] results in the following local equilibrium equations (i.e., Euler-Lagrange equations) in V and natural boundary conditions on S:
| \[\nabla \cdot {\bf{P}} = 0\] \[{\bf{P}} = {\left. {\left( {\partial W/\partial F} \right)} \right|_\xi }\] | (8) |
| \[\varsigma + df/d\xi = 2\kappa {\nabla ^2}\xi \] \[\varsigma = {\left. {\left( {\partial W/\partial \xi } \right)} \right|_{\bf{F}}}\] | (9) |
| \[{\bf{t}} = {\bf{P}} \cdot {\bf{n}}\] \[r = 2\kappa :\nabla \xi \otimes {\bf{n}}\] | (10) |
The first Piola-Kirchhoff stress tensor is P, and the unit outward normal vector to S is n.
The nonlinear theory of §2.2 is now specialized to isotropic behavior. This model, which is far more amenable to analytical and simple numerical solutions than that of §2.2, can be applied to gain insight into particular problems (e.g., 1D) wherein anisotropy is of secondary importance. Model kinematics, energy functions, and governing equations are again described in turn.
Equations (1)-(4) still apply. Inelastic deformation corresponding to amorphization is specified as the isotropic volume change (i.e., spherical eigenstrain)
| \[{{\bf{F}}^\xi } (\xi ) = {[\phi (\xi ) ]^{1/3}}1\] \[\phi (0) = 1\] \[\phi (1) = \Xi \] | (11) |
with f a sufficiently smooth, positive scalar function of the order parameter and with xintroduced in §2.1. A similar construction has been used elsewhere to model residual volume changes from point defects [40] and pore collapse [41]. Equation (4) then reduces to
| \[{\bf{C}} ({\bf{F}},\xi ) = {[\phi (\xi ) ]^{ - 2/3}}{{\bf{F}}^{\rm{T}}}{\bf{F}}\] \[J({\bf{F}},\xi ) = \det F/\varphi (\xi )\] | (12) |
Equations (5) and (6) still apply. A compressible neo-Hookean nonlinear elastic strain energy potential [20, 21, 25] is prescribed:
| \[W ({\bf{C}},\xi ) = {\textstyle{1 \over 2}}\mu ({\rm{tr}}{\bf{C}} - 3 - 2\ln J) + {\textstyle{1 \over 2}}\lambda { (\ln J) ^2}\] | (13) |
Elastic coefficients may depend on the order parameter ξ:
| \[\mu = {\mu _0}\chi (\xi ) \] \[\lambda = {\lambda _0}\iota (\xi ) \] \[{\lambda _0} = {B_0} - {\textstyle{2 \over 3}}{\mu _0}\] \[\chi (0) = \iota (0) = 1\] | (14) |
Here, c and i are sufficiently smooth scalar functions of the order parameter that interpolate between elastic constants of crystal and glass phases. Isotropic bulk and surface energies of the amorphous phase are represented by
| \[f(\xi ) = \Gamma {\xi ^2}/1\] \[\kappa :\nabla \xi \otimes \nabla \xi = \Gamma l|\nabla \xi {|^2}\] \[({\kappa _0} = \Gamma l\]β=0) | (15) |
where surface energy per unit reference area G and regularization length l have been introduced in §2.1. Total energy (5) then becomes
| \[\Psi ({\bf{x}},\xi ) = \int_V {[W(\nabla {\bf{x}},\xi ) + \Gamma {\xi ^2}/1 + \Gamma l|\nabla \xi {|^2}{\rm{]d}}V} \] | (16) |
with strain energy (13) expressed explicitly in terms of ξ and F=ÑX as
| \[W({\bf{F}},\xi ) = {\textstyle{1 \over 2}}{\mu _0}\chi (\xi )\{ {[\phi (\xi )]^{ - 2/3}}{\bf{F}}:{\bf{F}} - 3 - 2\ln [detF/\phi (\xi )]\} + {\textstyle{1 \over 2}}{\lambda _0}\iota (\xi ){\{ \ln [detF/\phi (\xi )]\} ^2}\] | (17) |
As a point of clarification, the term “interpolation function” is used herein to refer to any of functions f, c, and i that depend continuously on values of order parameter ξ. These functions are used to estimate values of specific volume and elastic coefficients in material wherein transformation is incomplete (i.e., wherein 0 < ξ< 1) , given, a priori, known values of such quantities at the endpoints ξ = 0 and ξ= 1 corresponding to pure crystalline and amorphous phases, respect ively.
Equations (7)-(10) still apply. Using (13) , stress in the second of (8) and elastic driving force in the second of (9) become, respectively,
| \[{\bf{P}}({\bf{F}},\xi ) = {\mu _0}\chi (\xi )\{ {[\phi (\xi )]^{ - 2/3}}{\bf{F}} - {{\bf{F}}^{ - {\rm{T}}}}\} + {\lambda _0}\iota (\xi )\ln [\det F\phi (\xi )]{{\bf{F}}^{ - {\rm{T}}}}\] | (18) |
| \[\begin{array}{l} \varsigma ({\bf{F}},\xi ) = \,\phi '(\xi )\{ {\mu _0}x(\xi )/\phi (\xi ) - {\textstyle{1 \over 3}}{\mu _0}\chi (\xi ){[\phi (\xi )]^{ - 5/3}}{\bf{F}}:{\bf{F}} - {\lambda _0}[\iota (\xi )/\phi (\xi )]\ln [\det F/\phi (\xi )]\} \\ \quad \quad \quad {\rm{ }} + {\kern 1pt} \,\chi '(\xi ){\mu _0}\{ {\textstyle{1 \over 2}}{[\phi (\xi )]^{ - 2/3}}{\bf{F}}:{\bf{F}} - {\textstyle{3 \over 2}} - \ln [\det F/\phi (\xi )]\} + {\textstyle{1 \over 2}}\iota '(\xi ){\lambda _0}{\{ \ln [\det F/\phi (\xi )]\} ^2} \end{array}\] | (19) |
where ξ¢ = dξ/dξ, c¢ = dc/dξ, and i¢ = di/d ξ. Cauchy stress tensor σ= (1/detF) PFT and Cauchy pressure p = -trσ/3 are, respectively,
| \[\sigma ({\bf{F}},\xi ) = [{\mu _0}x(\xi )/detF]\{ {[\phi (\xi )]^{ - 2/3}}{\bf{F}}{{\bf{F}}^{\rm{T}}} - 1\} + [{\lambda _0}\iota (\xi )/detF]\ln [detF/\phi (\xi )]1\] | (20) |
| \[p({\bf{F}},\xi ) = [{\mu _0}x(\xi )/\det F]\{ 1 - {\textstyle{1 \over 3}}{[\phi (\xi )]^{ - 2/3}}{\bf{F}}:{\bf{F}}\} - [{\lambda _0}\iota (\xi )/\det F]\ln [\det F/\phi (\xi )]\] | (21) |
Analyzed are solutions of the phase field theory of §2.3 for spatially homogeneous hydrostatic compression, followed by solutions for combined spherical compression and simple shear.
First consider uniform spherical deformation of an element of initially fully crystalline material from reference/initial volume V to current volume v:
| \[{\bf{x}} = {A^{1/3}}{\bf{X}}\] \[{\bf{F}} = {A^{1/3}}1\] \[A = \det {\bf{F}} = v/V > 0\] \[\nabla (A = 0)\] | (22) |
Under such spherical deformation, (18)-(21) reduce to
| \[{\bf{P}}(A,\xi ) = {\mu _0}\chi (\xi )\{ {[\phi (\xi )]^{ - 2/3}}{A^{1/3}} - {A^{ - 1/3}}\} 1 + {\lambda _0}\iota (\xi ){A^{ - 1/3}}\ln [A/\phi (\xi )]1\] | (23) |
| \[\begin{array}{l} \varsigma (A,\xi ) = \,\phi '(\xi )\{ {\mu _0}x(\xi )/\det F - {\mu _0}\chi (\xi ){[\phi (\xi )]^{ - 5/3}}{A^{2/3}} - {\lambda _0}[\iota (\xi )/\phi (\xi )]\ln [A/\phi (\xi )]\} \\ \quad \quad \quad {\rm{ }} + {\kern 1pt} \,\chi '(\xi ){\mu _0}\{ {\textstyle{3 \over 2}}{[\phi (\xi )]^{ - 2/3}}{A^{2/3}} - {\textstyle{3 \over 2}} - \ln [A/\phi (\xi )]\} + {\textstyle{1 \over 2}}\iota '(\xi ){\lambda _0}{\{ \ln [A/\phi (\xi )]\} ^2} \end{array}\] | (24) |
| \[\sigma (A,\xi ) = [{\mu _0}\chi (\xi )/A]\{ {[\phi (\xi )]^{ - 2/3}}{A^{2/3}} - 1\} 1 + [{\lambda _0}\iota (\xi )/A]\ln [A/\phi (\xi )]1\] | (25) |
| \[p(A,\xi ) = [{\mu _0}\chi (\xi )/A]\{ 1 - {[A/\phi (\xi )]^{2/3}}\} - [{\lambda _0}\iota (\xi )/A]\ln [A/\phi (\xi )]\] | (26) |
In Cartesian coordinates X = (X, y, z) and X = (X, Y, Z) , stress equilibrium in the first of (8) with (22) and (23) reduces to
| \[\partial {P_{xX}}/\partial X = \partial {P_{yY}}/\partial X = \partial {P_{zZ}}/\partial X = 0 \Rightarrow P = {P_{xX}} = {P_{yY}} = {P_{zZ}} = {\rm{constant}}\] | (27) |
| \[\nabla P(A,\xi ) = (\partial P/\partial A)\nabla A + (\partial P/\partial \xi )\nabla \xi = 0 \Rightarrow \xi = {\rm{constant}}\] | (28) |
Order parameter equilibrium in the first of (9) with equations (15) , (24) , and (28) becomes the algebraic equation
| \[\begin{array}{l} \xi = \, - {\textstyle{1 \over 2}}(l/\Gamma )\phi '[{\mu _0}\chi /\phi - {\mu _0}\chi {\phi ^{ - 5/3}}{A^{2/3}} - {\lambda _0}(\iota /\phi )\ln (A/\phi )]\\ {\rm{ }} - {\textstyle{1 \over 2}}(l/\Gamma ){\kern 1pt} \,\chi '{\mu _0}[{\textstyle{3 \over 2}}{\phi ^{ - 2/3}}{A^{2/3}} - {\textstyle{3 \over 2}} - \ln (A/\phi )] - {\textstyle{1 \over 4}}(l/\Gamma )\iota '{\lambda _0}{[\ln (A/\phi )]^2} \end{array}\] | (29) |
Solution of this equation requires specification of interpolation functions f (x) , c (x) , and i (x) . Similar to the polynomial form used elsewhere in a phase field model for twinning [19, 20, 21], let
| \[\phi = \Xi + (1 - \Xi ) [3{ (1 - \xi ) ^2} - 2{ (1 - \xi ) ^3}]\], \[\phi ' = - 6 (1 - \Xi ) [ (1 - \xi ) - { (1 - \xi ) ^2}]\] | (30) |
Similar to phase field models for fracture invoked elsewhere [22, 23, 24, 25], the shear modulus degrades as
| \[\chi = { (1 - \xi ) ^2}\] \[\chi ' = - 2 (1 - \xi ) \] | (31) |
This is consistent with the reported loss of shear strength in localized amorphous b and s in boron carbide [4, 14, 16]. Transformation can also be interpreted to correlate with mode II fracture in this model. Now let the ambient bulk modulus B0 remain constant upon amorphization, which requires from (31) that
| \[\begin{array}{l} \iota = {\beta _0}/{\lambda _0} - {\textstyle{2 \over 3}}{(1 - \xi )^2}{\mu _0}/{\lambda _0} = {\textstyle{1 \over 3}}[1 + {\nu _0} - {(1 - \xi )^2}(1 - 2{v_0})]/{\nu _0}\\ \iota ' = {\textstyle{2 \over 3}}(1 - \xi )(1 - 2{v_0})]/{\nu _0} \end{array}\] | (32) |
with n0 Poisson’s ratio for the crystalline phase. Prior DFT calculations [42] have suggested a ≈ 4% decrease in bulk modulus may occur upon structure transformation; this change is considered small enough, and of the same order of accuracy as the DFT solutions, to be justifiably ignored, thereby simplifying the theoretical framework and analytical solutions.
Solution data are obtained as follows for hydrostatic compressive loading. Volume is reduced incrementally by decreasing A from an initial condition of unity. For each volume decrement, (29) is solved via simple numerical iteration to obtain order parameter x. Once xis known, functions (30)-(32) are evaluated and then substituted into analytical expression (26) to determine pressure p. Compared in Figure 1 (a) are the pressure predicted from the present phase field model and results of quantum (DFT) calculations [11] for the polar C-B-C polytype, which were fit to a Birch-Murnaghan equation-of-state [43]. Agreement between the two sets of results is deemed excellent for A ³0.9, i.e., for volumetric compression less than around 10%. As shown in Figure 1 (b) , xremains very small for compressions up to 15%; in fact, the phase field model predicts x< 0.1 for A > 0.64. Such predictions agree with DFT simulations that do not indicate transformation or amorphization occurs in boron carbide for purely hydrostatic loading [11, 12]. A measure of intrinsic stability [6, 7, 8] under hydrostatic loading requires that the slope of the pressure-volume curve remains negative:
| \[ - {\rm{d}}p\,{\rm{d}}v = - {\rm{d}}p\,{\rm{d(}}AV) = - V(\partial P/\partial A){\kern 1pt} {({\rm{d}}A)^2} > 0 \Rightarrow \partial P/\partial A < 0\] | (33) |
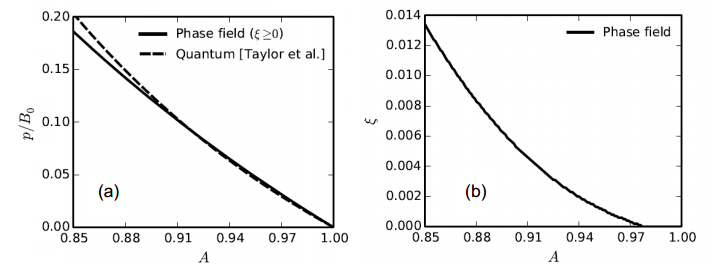 Figure 1. Pressure-volume response (a) and order parameter evolution (b) under uniform spherical compression.
Figure 1. Pressure-volume response (a) and order parameter evolution (b) under uniform spherical compression.
This stability condition, which correlates with a positive incremental/tangent bulk modulus, is clearly satisfied by the solutions in Figure 1 (a) , demonstrating mechanical stability of boron carbide under purely hydrostatic compression to large pressures.
Now consider spherical deformation of an element of initially fully crystalline material of length L superposed with shear displacement of magnitude u that potentially varies only with the X coordinate. In Cartesian coordinates, the deformation, deformation gradient matrix, Jacobian determinant, and shear strain are, respectively,
| \[\begin{array}{l} x = {A^{1/3}}X\\ y = {A^{1/3}}Y + \upsilon (X) \\ z = {A^{1/3}}Z \end{array}\] \[{\bf{F}} = \left[ {\begin{array}{*{20}{c}} {{A^{1/3}}}&0&0\\ \gamma &{{A^{1/3}}}&0\\ 0&0&{{A^{1/3}}} \end{array}} \right]\] \[A = \det {\bf{F}} > 0\] \[\gamma = d\upsilon /dx\] | (34) |
Here, A is constant with respect to reference coordinates (ÑA = 0) , but G may generally vary with X, where XÎ[0, L]. Under such shearing and volumetric deformation, (18) , (19) , and (21) reduce to
| \[\begin{array}{l} {P_{xX}}(A,\xi ) = {P_{yY}}(A,\xi ) = {P_{zZ}}(A,\xi )\\ {\rm{ }} = {\mu _0}\chi (\xi ){A^{ - 1/3}}\{ {[\phi (\xi )]^{ - 2/3}}{A^{2/3}} - 1\} + {\lambda _0}\iota (\xi ){A^{ - 1/3}}\ln [A/\phi (\xi )]\\ {P_{xY}}(A,\gamma ,\xi ) = \{ {\mu _0}\chi (\xi ) - {\lambda _0}\iota (\xi )\ln [A/\phi (\xi )]\} \gamma \\ {P_{yX}}(\gamma ,\xi ) = \{ {\mu _0}\chi (\xi ){[\phi (\xi )]^{ - 2/3}}\} \gamma = \tau \\ {P_{xZ}} = {P_{yZ}} = {P_{zX}} = {P_{zY}} = 0 \end{array}\] | (35) |
| \[\begin{array}{l} \varsigma (A,\gamma ,\xi ) = \,\phi '(\xi )\{ {\mu _0}x(\xi )/\phi (\xi ) - {\mu _0}\chi (\xi ){[\phi (\xi )]^{ - 5/3}}{A^{2/3}} - {\lambda _0}[\iota (\xi )/\phi (\xi )]\ln [A/\phi (\xi )]\} \\ \quad \quad \quad {\rm{ }} + {\kern 1pt} \,\chi '(\xi ){\mu _0}\{ {\textstyle{3 \over 2}}{[\phi (\xi )]^{ - 2/3}}{A^{2/3}} - {\textstyle{3 \over 2}} - \ln [A/\phi (\xi )] + {\textstyle{1 \over 2}}{\gamma ^2}\} + {\textstyle{1 \over 2}}\iota '(\xi ){\lambda _0}{\{ \ln [A/\phi (\xi )]\} ^2} \end{array}\] | (36) |
| \[p(A,\gamma ,\xi ) = [{\mu _0}{\rm{x}}(\xi )/\phi (\xi )]\{ 1 - {[A/\phi (\xi )]^{2/3}} - {\textstyle{1 \over 3}}{[\phi (\xi )]^{ - 2/3}}{\gamma ^2}\} - [{\lambda _0}\iota (\xi )/\phi (\xi )]\ln [A/\phi (\xi )]\] | (37) |
In the third line of (35) , shear stress t is work conjugate to G in the energy increment per unit reference volume P:dF. Stress equilibrium (8) with (34) and (35) , presuming stresses, like deformation, can only vary with the X coordinate, reduces to
| \[\partial {P_{_{xX}}}/\partial X = \partial {P_{_{{\rm{y}}X}}}/\partial X = \partial \tau /\partial X = 0\] | (38) |
Order parameter equilibrium in the first of (9) with (15) and (36) becomes
| \[\begin{array}{l} \xi = \, - {\textstyle{1 \over 2}}(l/\Gamma )\phi '[{\mu _0}\chi /\phi - {\mu _0}\chi {\phi ^{ - 5/3}}{A^{2/3}} - {\lambda _0}(\iota /\phi )\ln (A/\phi )]\\ {\rm{ }} - {\textstyle{1 \over 2}}(l/\Gamma ){\kern 1pt} \,\chi '{\mu _0}[{\textstyle{3 \over 2}}{\phi ^{ - 2/3}}{A^{2/3}} - {\textstyle{3 \over 2}} - \ln (A/\phi ) + {\textstyle{1 \over 2}}{\gamma ^2}] - {\textstyle{1 \over 4}}(l/\Gamma ){\kern 1pt} \iota '{\lambda _0}{[\ln (A/\phi )]^2} \end{array}\] | (39) |
The same interpolation functions first introduced in (30)-(32) are invoked the remainder of this work.
First sought are spatially homogeneous solutions to (35)-(39) wherein deformation gradient and order parameter do not vary with position X:
| \[A = {\rm{constant}},\quad \gamma = {\rm{constant,}}\quad \xi = {\rm{constant}}\] | (40) |
From (35) , such solutions clearly satisfy stress equilibrium (38) . Also compared later is the ratio of total energy with possible transformation to elastic energy for the case when no phase transformation occurs, where for the spatially homogeneous solution,
| \[\begin{array}{l} \bar \Psi = \Psi /V = (1/V)\int_V {[W(A,\gamma ,\xi ) + \Gamma {\xi ^2}/l]{\rm{d}}V} = W(A,\gamma ,\xi ) + \Gamma {\xi ^2}/l\\ {W_0}(A,\gamma ) = {\textstyle{1 \over 2}}{\mu _0}[3({A^{2/3}} - 1) - 2\ln A + {\gamma ^2}] + {\textstyle{1 \over 2}}{\lambda _0}{(\ln A)^2} \end{array}\] | (41) |
Homogeneous solution data are obtained as follows for shear and compressive loading. Volume is reduced incrementally by reducing A from unity in decrements of 0.02. For each volume decrement, shear g is increased incrementally from zero to 0.15. Equilibrium equation (39) is solved via simple numerical iteration to obtain order parameter ξ. Once ξ is known, functions (30)-(32) are evaluated and then substituted into analytical expressions (35) , (37) , and (41) to determine stress components, pressure, and energies. Shown in Figure 2 (a) is the shear stress t (normalized by initial shear modulus) predicted from the phase field model at various compressive strains A. Complementary results for the order parameter and pressure (normalized by initial bulk modulus) are given in Figures 2 (b) and 2 (c) . As volumetric compression increases (i.e., as A is reduced) , pressure increases, transformation to the amorphous phase becomes more rapid, and shear strength diminishes. Complete amorphization is approached as shear strains become large, i.e., ξ®1 for g>0.15. Such phase field predictions agree with trends observed in DFT [11, 12] that amorphization in boron carbide is triggered by non-hydrostatic loading involving shear strain and is accelerated by increasing superposed compressive stress. As indicated by ratio values less than unity in Figure 2 (d) , the total energy of the phase field solution is always less than that of the purely elastic solution (ξ= 0) for neo-Hookean elasticity, demonstrating metastability of the latter model relative to the phase field model. Intrinsic stability at constant volumetric deformation A under dead loading by shear stress t requires [6, 8, 16]
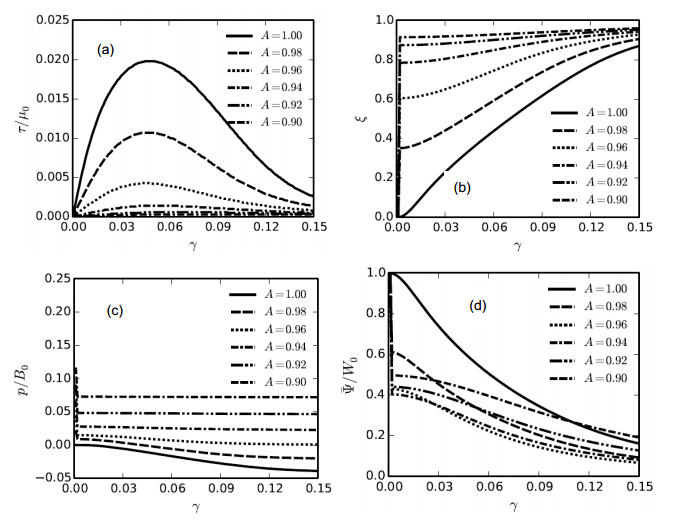 Figure 2. Shear stress (a) , order parameter (b) , Cauchy pressure (c) , and ratio of total energy to energy for purely elastic deformation (d) for simple shear Gunder spherical compression A.
Figure 2. Shear stress (a) , order parameter (b) , Cauchy pressure (c) , and ratio of total energy to energy for purely elastic deformation (d) for simple shear Gunder spherical compression A.
| \[{\rm{d}}{\bf{P}}:{\rm{d}}{\bf{F}} = {\rm{d}}{P_{yX}}{\rm{d}}{F_{yX}} = {\rm{d}}\tau {\kern 1pt} \,{\rm{d}}\gamma = \partial \tau /\partial {\kern 1pt} \gamma {({\rm{d}}\gamma )^2} > 0 \Rightarrow \partial \tau /\partial {\kern 1pt} \gamma > 0\] | (42) |
This condition, which correlates with a positive incremental/tangent shear modulus, is first violated by each of the solutions in Figure 2 (a) when shear stress treaches a maximum or critical value tC, demonstrating mechanical instability of boron carbide under simple shear loading possibly superposed on constant volumetric compression. Peak stresses at the onset of such instability are listed along with other solution variables in Table 2. As volume decreases, peak shear stress decreases, pressure increases, and the value of the order parameter at instability increases.
| Volume ratio A | Peak stress tC [GPa] | Shear gC | Order parameter xC | Pressure pC [GPa] |
| 1.00 | 3.91 | 0.048 | 0.36 | -3.02 |
| 0.98 | 2.11 | 0.047 | 0.53 | -0.43 |
| 0.96 | 0.84 | 0.046 | 0.70 | 2.33 |
| 0.94 | 0.28 | 0.052 | 0.84 | 6.35 |
| 0.92 | 0.12 | 0.067 | 0.91 | 11.78 |
| 0.90 | 0.07 | 0.081 | 0.94 | 17.96 |
Now sought are spatially heterogeneous [ξ = ξ (X) ] but stress-free solutions corresponding to vanishing of P in (35) under null compression and omitting volume collapse upon transformation:
| \[\begin{array}{l} A = \Xi \to 1 \Rightarrow \det {\bf{F}} = \phi = 1\\ \Rightarrow {P_{xX}} = {P_{yY}} = {P_{zZ}} = 0\\ \quad {\rm{ }}\tau (\gamma ,\xi ) = {P_{xY}} (\gamma ,\xi ) = {P_{yX}} (\gamma ,\xi ) = {\mu _0}\chi (\xi ) \gamma = {\mu _0}{ (1 - \xi ) ^2}\gamma = 0\\ \quad \;\varsigma (\gamma ,\xi ) = {\textstyle{1 \over 2}}{\mu _0}\chi ' (\xi ) {\gamma ^2} = - {\mu _0} (1 - \xi ) {\gamma ^2} \end{array}\] | (43) |
The final two lines in (43) combine to imply elastic driving force in (36) must also vanish and that shear strain can be nonzero only in regions where amorphization is complete:
| \[\varsigma = - \tau \gamma /(1 - \xi ) = 0,\quad \gamma (X) = 0\forall \xi (X) < 1\] | (44) |
Order parameter equilibrium in the first of (9) becomes, for the present one-dimensional shear problem with r = 0 boundary conditions and full amorphization at the midpoint of the domain,
| \[{\partial ^2}\xi /\partial {X^2} - \xi /{l^2} = 0\] \[{\left. {(\partial \xi /\partial X)} \right|_{X = 0}} = {\left. {(\partial \xi /\partial X)} \right|_{X = L}} = 0\] \[{\left. \xi \right|_{X = L/2}} = 1\] | (45) |
This is a homogeneous, ordinary second-order differential equation with exact solution
| \[\xi (X) = \left\{ {\begin{array}{*{20}{c}} {{{[{e^{L/(2l)}} + {e^{ - L/(2l)}}]}^{ - 1}}({e^{X/l}} + {e^{ - X/l}}){\rm{ }}\,{\rm{for }}X \le L/2}\\ {{{[{e^{L/(2l)}} + {e^{3L/(2l)}}]}^{ - 1}}{e^{X/l}} + {{[{e^{ - L/(2l)}} + {e^{ - 3L/(2l)}}]}^{ - 1}}{e^{ - X/l}}{\rm{ for }}X \ge L/2} \end{array}} \right.\] | (46) |
Total energy per unit cross sectional area is, noting that (43) and (44) imply W = 0,
| \[\int_0^L {\Gamma [{\xi ^2}/l + l{{(\partial \xi /\partial X)}^2}]{\rm{d}}X} = 2\Gamma ({e^{L/l}} - {e^{ - L/l}}){[{e^{L/(2l)}} + {e^{ - L/(2l)}}]^{ - 2}} \approx 2\Gamma \] | (47) |
where the final approximation effectively becomes exact for L > 10l. This calculation verifies that G is indeed the surface energy of a localized amorphous b and , the factor of two in (47) accounting for each side of the b and surface. Shown in Figure 3 (a) is the heterogeneous solution (46) for a domain length of L = 25l, verifying that the width of the localized amorphous b and wherein x ³ 0.75 is approximately l. Shown in Figure 3 (b) is the ratio of total energy from the homogeneous phase field solution under null volumetric compression (i.e., pure simple shear loading) to the total surface energy of the localized solution verified in (47) . When this ratio in Figure 3 (b) exceeds a value of unity—which occurs at G ≈ 0.0125—the localized stress-free solution is energetically favorable to the homogeneous solution, suggesting local transformation and fracture may be expected.
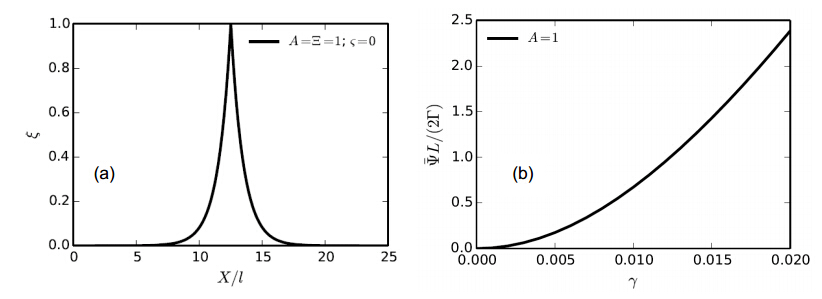 Figure 3. Order parameter profile for localized stress-free solution (a) and ratio of total energy for homogeneous phase field solution to surface energy (b) under simple shear G.
Figure 3. Order parameter profile for localized stress-free solution (a) and ratio of total energy for homogeneous phase field solution to surface energy (b) under simple shear G.
The phase field theory developed and applied in the present paper consists of the following principal components:
· Order parameter denoting transformation from crystal to amorphous/glass phase (2)
· Volumetric inelastic deformation (11) associated with mass density increase upon amorphization
· Compressible neo-Hookean nonlinear elastic strain energy (13)
· Interpolation function (30) relating order parameter increase and volume decrease (spherical eigenstrain) similar to that used to interpolate eigenshear in twinning models [19, 20, 21]
· Degraded shear modulus and fixed bulk modulus upon amorphization
· Interpolation function (31) relating order parameter increase and shear modulus decrease similar to that used to reduce elastic modulus in fracture models [22, 23, 24, 25, 30]
The only parameters entering the phase field component of the theory are surface energy and localization width, which are obtained directly from atomic theory [9] and experiment [4, 14]. The initial bulk modulus of the neo-Hookean potential is fit to uniquely to DFT pressure-volume data [11], and the initial shear modulus is obtained directly from second-order elastic constants of DFT [10, 11]. Thus, the phase field model is considered purely predictive, with no adjustable parameters. Of course, interpolation functions such as (30)-(32) could be generalized or altered as needed in the future to match additional data for other stress-deformation states as such data become available from more extensive experimentation and atomic simulation. Furthermore, the model should be implemented in a numerical framework such as the finite element method [19, 20, 21, 25] to study boundary value problems involving more complicated geometries and boundary conditions. Extension of the theory towards a homogenized polycrystal model [16, 44] wherein multiple anisotropic B4C crystals occupy a single material point in a computation is also foreseeable.
The present results suggest that boron carbide, under simple shear loading, should become unstable, undergo substantial amorphization, and demonstrate severe strength loss at shear strains on the order of 5%, with peak shear strengths on the order of 4 GPa, the latter value decreasing with increasing superposed pressure (Table 2) . While the trends in phase field results agree with DFT predictions, maximum shear stresses observed in DFT can exceed 20 GPa, with shear strains at instability or peak load on the order of 10-15 % [11]. It is suggested that the present phase field predictions are more physically realistic when compared to real solids with defects, since it is unlikely that any brittle material could sustain such large shear stresses without undergoing mode II fracture which appears prohibited by the small system size and boundary conditions used in DFT. A complementary interpretation is that the present phase field model of shear degradation accounts for simultaneous amorphization and fracture as suggested by the form of (31) , whereas prior results reported from DFT [4, 10, 11, 12] account for structure collapse but not complete bond breaking.
The present theory and solutions do not account explicitly for the presence of defects in the crystal, such as point defects, dislocations, stacking faults, and twin boundaries, all of which are known to exist in boron carbide ceramics [4, 14, 32, 33]. The model and analysis may be altered in a simple empirical way to account for defects simply by increasing or decreasing the surface energy Gaccording to whether initial defect concentrations increase or decrease the energetic barrier for localization. For example, if a stacking fault promotes local amorphization, G may be lowered by some suitable fraction of the stacking fault energy. Alternatively, for a more realistic and predictive representation of effects of defects, the phase field theory should be extended to include additional order parameters describing (partial) dislocations and deformation twins [18, 19, 20, 21, 45], and numerical simulations wherein initial defect geometries are resolved explicitly should be considered, as has been done elsewhere in a study of heterogeneous stress distributions in highly twinned, slip-cast boron carbide [33]. Regardless, dislocation-type defects are thought to be relatively immobile as evidenced by the low ductility and high stiffness of boron carbide.
The model and analysis reported in this work has been limited to quasi-static loading. In impact or ballistic loading, local stress field perturbations associated with elastic wave interactions (e.g., shear and bulk compression waves) and heterogeneities (e.g., crystal defects and grain boundaries) are expected to promote amorphization. This expectation is supported by previous nonlinear analysis and simulations invoking a Born-like instability criterion for localization [16, 17], wherein dynamic deformation facilitated instability relative to static loading. The level of amorphization or structural disorder in boron carbide has also been reported as greater in dynamic indentation experiments compared to static indentation experiments [13, 46].
A nonlinear phase field theory has been developed and applied towards amorphization and shear failure in boron carbide ceramic. Analytical and iterative numerical solutions have been obtained for hydrostatic loading and for simple shear loading in conjunction with constant volumetric compression. Model predictions agree with trends reported elsewhere in experiments and quantum mechanical (DFT) simulations: transformation does not occur under purely hydrostatic loading; transformation occurs under shear loading and is promoted by superposed compressive stress; the tangent shear modulus and shear strength decrease and the material response becomes unstable upon application of sufficient shear stress or shear strain. The proposed theory, which essentially includes no adjustable or free parameters, appears to be the first phase field model of pressure-shear induced amorphization in crystalline solids.
The authors declare there is no conflict and interest.
| [1] | Gregoryanz E, Hemley R, Mao H, et al. (2000) High pressure elasticity of α-quartz: instability and ferroelastic transition.Phys Rev Lett 84: 3117-3120. |
| [2] | Watson G, Parker S (1995) Dynamical instabilities in α-quartz and α-berlinite: a mechanism for amorphization.Phys Rev B 52: 13306-13309. |
| [3] | Goel P, Mittal R, Choudhury N, et al. (2010) Lattice dynamics and Born instability in yttrium aluminum garnet, Y3Al5O12..J Phys: Condens Mat 22: 065401. |
| [4] | Yan X, Tang Z, Zhang L, et al. (2009) Depressurization amorphization of single-crystal boron carbide.Phys Rev Lett 102: 075505. |
| [5] | Born M (1940) On the stability of crystal lattices I.Math Proc Cambridge 36: 160-172. |
| [6] | Hill R (1975) On the elasticity and stability of perfect crystals at finite strain.Math Proc Cambridge 77: 225-240. |
| [7] | Morris J, Krenn C (2000) The internal stability of an elastic solid.Phil Mag A 80: 2827-2840. |
| [8] | Clayton J, Bliss K (2014) Analysis of intrinsic stability criteria for isotropic third-order Green elastic and compressible neo-Hookean solids.Mech Mater 68: 104-119. |
| [9] | Fanchini G, McCauley J, Chhowalla M (2006) Behavior of disordered boron carbide under stress.Phys Rev Lett 97: 035502. |
| [10] | Taylor D, Wright T, McCauley J (2011) First principles calculation of stress induced amorphization in armor ceramics. US Army Research Lab Res Rep ARL-MR-0779.Aberdeen Proving Ground, MD . |
| [11] | Taylor D, McCauley J, Wright T (2012) The effects of stoichiometry on the mechanical properties of icosahedral boron carbide under loading.J Phys: Condens Mat 24: 505402. |
| [12] | Aryal S, Rulis P, Ching W (2011) Mechanism for amorphization of boron carbide B4C under uniaxial compression.Phys Rev B 84: 184112. |
| [13] | Subhash G, Maiti S, Geubelle P, Ghosh D (2008) Recent advances in dynamic indentation fracture, impact damage and fragmentation of ceramics.J Am Ceram Soc 91: 2777-2791. |
| [14] | Chen M, McCauley J, Hemker K (2003) Shock-induced localized amorphization in boron carbide.Science 299: 1563-1566. |
| [15] | Grady D (2011) Adiabatic shear failure in brittle solids.Int J Impact Eng 38: 661-667. |
| [16] | Clayton J (2012) Towards a nonlinear elastic representation of finite compression and instability of boron carbide ceramic.Phil Mag 92: 2860-2893. |
| [17] | Clayton J (2013) Mesoscale modeling of dynamic compression of boron carbide polycrystals.Mech Res Commun 49: 57-64. |
| [18] | Koslowski M, Cuitino A, Ortiz M (2002) A phase-field theory of dislocation dynamics, strain hardening, and hysteresis in ductile single crystals.J Mech Phys Solids 50: 2597-2635. |
| [19] | Clayton J, Knap J (2011) A phase field model of deformation twinning: nonlinear theory and numerical simulations.Physica D 240: 841-858. |
| [20] | Clayton J, Knap J (2011) Phase field modeling of twinning in indentation of transparent single crystals.Model Simul Mater Sci Eng 19: 085005. |
| [21] | Clayton J, Knap J (2013) Phase-field analysis of fracture induced twinning in single crystals.Acta Mater 61: 5341-5353. |
| [22] | Kuhn C, Müller R (2012) Interpretation of parameters in phase field models for fracture.Proc Appl Math Mec 12: 161-162. |
| [23] | Borden M, Verhoosel C, Scott M, et al. (2012) A phase-field description of dynamic brittle fracture.Comput Method Appl Mech Eng 271: 77-95. |
| [24] | Voyiadjis G, Mozaffari N (2013) Nonlocal damage model using the phase field method: theory and applications.Int J Solids Structures 50: 3136-3151. |
| [25] | Clayton J, Knap J (2014) A geometrically nonlinear phase field theory of brittle fracture.Int J Fracture, submitted . |
| [26] | Clayton J (2005) Dynamic plasticity and fracture in high density polycrystals: constitutive modeling and numerical simulation.J Mech Phys Solids 53: 261-301. |
| [27] | Clayton J (2009) A continuum description of nonlinear elasticity, slip and twinning, with application to sapphire.Proc R Soc Lond A 465: 307-334. |
| [28] | Clayton J (2010) Modeling nonlinear electromechanical behavior of shocked silicon carbide.J Appl Phys 107: 013520. |
| [29] | Clayton J (2010) Analysis of shock compression of strong single crystals with logarithmic thermoelastic-plastic theory.Int J Eng Sci 79: 1-20. |
| [30] | Benallal A, Marigo J (2007) Bifurcation and stability issues in gradient theories with softening.Model Simul Mater Sci Eng 15: S283-S295. |
| [31] | Clayton J (2011) Nonlinear Mechanics of Crystals, Dordrecht.Springer . |
| [32] | Ashbee K (1971) Defects in boron carbide before and after irradiation.Acta Metall 19: 1079-1085. |
| [33] | Sano T, Randow C (2011) The effect of twins on the mechanical behavior of boron carbide.Metall Mater Trans A 42: 570-574. |
| [34] | Clayton J (2010) On anholonomic deformation, geometry, and differentiation.Math Mech Solids 17: 702-735. |
| [35] | Clayton J (2010) Deformation, fracture, and fragmentation in brittle geologic solids.Int J Fracture 163: 151-172. |
| [36] | Clayton J, McDowell D, Bammann D (2006) Modeling dislocations and disclinations with finite micropolar elastoplasticity.Int J Plasticity 22: 210-256. |
| [37] | Clayton J (2013) Defects in nonlinear elastic crystals: differential geometry, finite kinematics, and second-order analytical solutions.Z Angew Math Mech (ZAMM) in press . |
| [38] | Clayton J (2014) An alternative three-term decomposition for single crystal deformation motivated by non-linear elastic dislocation solutions.Q J Mech Appl Math 67: 127-158. |
| [39] | Clayton J, Bammann D, McDowell D (2005) A geometric framework for the kinematics of crystals with defects.Phil Mag 85: 3983-4010. |
| [40] | Clayton J (2009) A non-linear model for elastic dielectric crystals with mobile vacancies.Int J Non-Linear Mech 44: 675-688. |
| [41] | Clayton J (2008) A model for deformation and fragmentation in crushable brittle solids.Int J Impact Eng 35: 269-289. |
| [42] | Ivaneshchenko V, Shevchenko V, Turchi P (2009) First principles study of the atomic and electronic structures of crystalline and amorphous B4C.Phys Rev B 80: 235208. |
| [43] | Clayton J (2013) Nonlinear Eulerian thermoelasticity for anisotropic crystals.J Mech Phys Solids 61: 1983-2014. |
| [44] | Clayton J, McDowell D (2003) A multiscale multiplicative decomposition for elastoplasticity of polycrystals.Int J Plasticity 19: 1401-1444. |
| [45] | Hu S, Henager C, Chen LQ (2010) Simulations of stress-induced twinning and de-twinning: a phase field model.Acta Mater 58: 6554-6564. |
| [46] | Ghosh D, Subhash G, Lee C, et al. (2007) Strain-induced formation of carbon and boron clusters in boron carbide during dynamic indentation.Appl Phys Lett 91: 061910. |
| 1. | J.D. Clayton, R.B. Leavy, J. Knap, Phase field modeling of heterogeneous microcrystalline ceramics, 2019, 166, 00207683, 183, 10.1016/j.ijsolstr.2019.02.016 | |
| 2. | J. D. Clayton, M. Guziewski, J. P. Ligda, R. B. Leavy, J. Knap, A Multi-Scale Approach for Phase Field Modeling of Ultra-Hard Ceramic Composites, 2021, 14, 1996-1944, 1408, 10.3390/ma14061408 | |
| 3. | J. D. Clayton, Finsler-geometric continuum dynamics and shock compression, 2017, 208, 0376-9429, 53, 10.1007/s10704-017-0211-5 | |
| 4. | John D. Clayton, 2019, Chapter 10, 978-3-030-15329-8, 329, 10.1007/978-3-030-15330-4_10 | |
| 5. | John D. Clayton, 2019, Chapter 11, 978-3-030-15329-8, 385, 10.1007/978-3-030-15330-4_11 | |
| 6. | J. D. Clayton, Generalized Finsler geometric continuum physics with applications in fracture and phase transformations, 2017, 68, 0044-2275, 10.1007/s00033-016-0752-x | |
| 7. | J. D. Clayton, J. Knap, Continuum modeling of twinning, amorphization, and fracture: theory and numerical simulations, 2018, 30, 0935-1175, 421, 10.1007/s00161-017-0604-8 | |
| 8. | J. D. Clayton, Finsler-geometric continuum mechanics and the micromechanics of fracture in crystals, 2016, 01, 2424-9130, 1640003, 10.1142/S2424913016400038 | |
| 9. | J. D. Clayton, Mesoscale models of interface mechanics in crystalline solids: a review, 2018, 53, 0022-2461, 5515, 10.1007/s10853-017-1596-2 | |
| 10. | J. D. Clayton, On Finsler Geometry and Applications in Mechanics: Review and New Perspectives, 2015, 2015, 1687-9120, 1, 10.1155/2015/828475 | |
| 11. | J.D. Clayton, A.L. Tonge, A nonlinear anisotropic elastic–inelastic constitutive model for polycrystalline ceramics and minerals with application to boron carbide, 2015, 64-65, 00207683, 191, 10.1016/j.ijsolstr.2015.03.024 | |
| 12. | Shawn P. Coleman, Efrain Hernandez-Rivera, Kristopher D. Behler, Jennifer Synowczynski-Dunn, Mark A. Tschopp, Challenges of Engineering Grain Boundaries in Boron-Based Armor Ceramics, 2016, 68, 1047-4838, 1605, 10.1007/s11837-016-1856-7 | |
| 13. | J. D. Clayton, Generalized pseudo-Finsler geometry applied to the nonlinear mechanics of torsion of crystalline solids, 2018, 15, 0219-8878, 1850113, 10.1142/S021988781850113X | |
| 14. | J.D. Clayton, J. Knap, Phase field modeling of directional fracture in anisotropic polycrystals, 2015, 98, 09270256, 158, 10.1016/j.commatsci.2014.11.009 | |
| 15. | J. D. Clayton, J. Knap, Geometric micromechanical modeling of structure changes, fracture and grain boundary layers in polycrystals, 2018, 03, 2424-9130, 1840001, 10.1142/S2424913018400015 |
| Property | Description | Value [units] |
| B0 | bulk modulus (crystal) | 248 GPa |
| m0 | shear modulus (crystal) | 197 GPa |
| l | localization width (glass) | 2 nm |
| Γ | surface energy (glass) | 347 mJ×m-2 |
| Ξ | density ratio (crystal/glass) | 0.96 |
| Volume ratio A | Peak stress tC [GPa] | Shear gC | Order parameter xC | Pressure pC [GPa] |
| 1.00 | 3.91 | 0.048 | 0.36 | -3.02 |
| 0.98 | 2.11 | 0.047 | 0.53 | -0.43 |
| 0.96 | 0.84 | 0.046 | 0.70 | 2.33 |
| 0.94 | 0.28 | 0.052 | 0.84 | 6.35 |
| 0.92 | 0.12 | 0.067 | 0.91 | 11.78 |
| 0.90 | 0.07 | 0.081 | 0.94 | 17.96 |
| Property | Description | Value [units] |
| B0 | bulk modulus (crystal) | 248 GPa |
| m0 | shear modulus (crystal) | 197 GPa |
| l | localization width (glass) | 2 nm |
| Γ | surface energy (glass) | 347 mJ×m-2 |
| Ξ | density ratio (crystal/glass) | 0.96 |
| Volume ratio A | Peak stress tC [GPa] | Shear gC | Order parameter xC | Pressure pC [GPa] |
| 1.00 | 3.91 | 0.048 | 0.36 | -3.02 |
| 0.98 | 2.11 | 0.047 | 0.53 | -0.43 |
| 0.96 | 0.84 | 0.046 | 0.70 | 2.33 |
| 0.94 | 0.28 | 0.052 | 0.84 | 6.35 |
| 0.92 | 0.12 | 0.067 | 0.91 | 11.78 |
| 0.90 | 0.07 | 0.081 | 0.94 | 17.96 |